Ellis A.M., Feher M., Wright T. Electronic and Photoelectron Spectroscopy: Fundamentals and Case Studies

Подождите немного. Документ загружается.

The principles of point group symmetry and group theory

265

∞h

E 2C

∞

... ∞σ

i 2S

∞

... ∞C



11 ... 1 1 1 ... 1 x

+ y

, z



−

11 ... −111 ... −1 R



22cos φ ... 0 2 −2 cos φ ... 0 (R

, R

) (xz, yz)



22cos 2φ ... 0 2 2cos 2φ ... 0 (x

−y

, xy)

... ... ... ... ... ... ... ... ...



11 ... 1 −1 −1 ... −1 z



−

11 ... −1 −1 −1 ... 1



22cos φ ... 0 −22cos φ ... 0 (x, y)



22cos 2φ ... 0 −2 −2 cos 2φ ... 0

... ... ... ... ... ... ... ... ...

Appendix E

More on electronic

conﬁgurations and electronic

states: degenerate orbitals

and the Pauli principle

The Pauli exclusion principle states that no two electrons in an atom or molecule can share

entirely the same set of quantum numbers. This requirement follows from the nature of

electronic wavefunctions, which must be antisymmetric with respect to the exchange of any

identical electrons. This has an impact in the determination of the electronic states possible

from a given electronic conﬁguration.

E.1 Atoms

Consider, for example, the carbon atom, which has a ground electronic conﬁguration

. Suppose that one of the 2p electrons is excited to a 3p orbital. To determine

the electronic states that are possible from this conﬁguration, the process described in

Section 4.1 can be followed. The 1s and 2s orbitals are full and so we can focus on the p

electrons only. The possible values of the total orbital angular momentum quantum number

L are 2, 1 or 0. Similarly, the total spin quantum number must be 1 or 0 and so the possible

electronic states that result from the 1s

conﬁguration are

S, and

S. It is therefore initially tempting to propose that electronic states of the same spatial and

spin symmetry arise from the ground electronic conﬁguration. Such an assumption would

be wrong because it ignores the Pauli principle.

In contrast to the excited conﬁguration considered above, in the ground conﬁguration of

the carbon atom the two p electrons have the same principal quantum numbers. To satisfy the

Pauli principle, we must therefore avoid those electronic states of the carbon atom in which

the two p electrons possess exactly the same values for the remaining quantum numbers.

This means that the electrons cannot be in a 2p orbital with the same m

and m

quantum

numbers. The acceptable arrangements of the electrons within the three 2p orbitals are

summarized in Table E.1. Notice that in contrast to the excited conﬁguration 1s

only three electronic states (

D, and

S) are possible from the conﬁguration 1s

266

Degenerate orbitals and the Pauli principle

267

Table E.1 Possible arrangement of electrons for

a2p

conﬁguration

=−1 m

= 0 m

=+1 Electronic state

↑↑

↓↑

↓↓

↑↑

↓↑











↓↓

↑↑

↓↑

↓↓

↑↓











↑↓

Constructing a table of electron arrangements amongst orbitals such as that shown in

Table E.1 is clearly a cumbersome process. A neater way of arriving at the same con-

clusions follows from the symmetries of the orbital and spin wavefunctions with respect

to the exchange of identical particles. Taking spin ﬁrst, the spin wavefunction for a singlet

state is



√

[α(1)β(2) − α(2)β(1)] (E.1)

Triplet states have three possible wavefunctions due to the three-fold degeneracy of unit

angular momentum states (cf. p orbitals in atoms), which are given by



(+1)

= α(1)α(2) (E.2)



(0)

√

[α(1)β(2) + β(1)α(2)] (E.3)



(−1)

= β(1)β(2) (E.4)

In the above expressions the labels 1 and 2 refer to the two electrons and α and β refer,

respectively, to spin up (m

) and spin down (m

=−

)wavefunctions for the individual

electrons. The superscripts on the wavefunctions on the left-hand side of each equation refer

to the spin projection quantum number, M

,which can have the values 1, 0 or −1 for the

case where S = 1.

Interchange of the two electrons corresponds to switching the locations of the 1 and 2

labels in parentheses. For the singlet state, this changes the sign of the wavefunction so the

spin singlet wavefunction is antisymmetric with respect to exchange of identical electrons.

268 Appendix E

In contrast, all three triplet wavefunctions remain unchanged on switching the electron

indices and so triplet wavefunctions are symmetric with respect to electron exchange.

The symmetry of the spatial (orbital angular momentum) part of the electronic wave-

function with respect to electron exchange can also be determined straightforwardly, but

we shall avoid the details. In effect, the desired wavefunction is a linear combination of

the wavefunctions for the individual 2p orbitals in much the same way as the spin wave-

functions can be expressed as linear combinations of the individual spin up and spin down

wavefunctions, α and β. The key result is that electronic states with L even are symmetric

with respect to electron exchange, whereas those with L odd are antisymmetric. Thus L even

states can only combine with the singlet spin function in order to satisfy the Pauli principle,

and so we deduce that the only possible singlet states are

D and

S. Similarly, only one

triplet state can be formed,

E.2 Molecules

Exactly the same ideas apply to molecules. In molecules, as in atoms, equivalent orbitals

are degenerate orbitals and these only arise for molecules that possess relatively high sym-

metries. Consider, for example, a molecule with C

symmetry and all orbitals ﬁlled except

the outer pair, which have e

symmetry. Now suppose that there are two electrons in the

orbitals. This is clearly a case where the Pauli principle needs to be taken into account.

As we have seen elsewhere (Section 4.2), the possible spatial symmetries of the overall

electronic state can be obtained by taking the direct product of the symmetries of the indi-

vidual orbitals, e

⊗ e

. The result can be obtained from Table D.4 in Appendix D, and is

+ [A

] + E

The square brackets around the A

representation are employed to show that this corre-

sponds to an antisymmetrized product (see Section D.8), which means that the A

spatial

wavefunction arising from the orbital conﬁguration (e

)

is antisymmetric with respect to

electron exchange. Consequently, only a triplet spin state is possible for this spatial symme-

try. In contrast the A

and E

spatial wavefunctions are symmetric with respect to electron

exchange and can only combine with a singlet spin state. Thus we deduce that the possible

electronic states arising from the (e

)

conﬁguration are

, and

Appendix F

Nuclear spin statistics

Some atomic nuclei possess spin angular momentum, and this can couple with other angular

momenta in a molecule, notably the overall rotational angular momentum, and with the net

electron spin (if any), to cause additional structure in a spectrum. This additional structure

is known as hyperﬁne structure. Hyperﬁne splittings are normally very small and are only

resolved in very high resolution spectroscopy. However, the effect of nuclei on molecular

spectra can also be observed in lower resolution experiments through the phenomenon

known as nuclear spin statistics. This manifests itself as an alternation of intensities in the

rotational structure for molecules with a rotational symmetry C

or higher. Examples were

met in the Case Studies described in Chapters 16, 21, and 28.

A general expression for the total wavefunction of the molecule was given by equa-

tion (7.11). In reality, the total wavefunction also includes one more term, the wavefunction

due to nuclear spin, ψ

(r, R) = ψ

(r, R

).ψ

(R).ψ

(F.1)

For purposes of this discussion, nuclei with half-integer spins (such nuclei are called

fermions because they obey Fermi–Dirac statistics) must be differentiated from those with

integer spins (called bosons because they can be described using Bose–Einstein statistics).

The generalized Pauli principle states that the total wavefunction of the system must be

antisymmetric with respect to the exchange of two identical fermions but symmetric for the

exchange of identical bosons.

To establish the symmetry of the overall molecular wavefunction with respect to exchange

of identical nuclei, it is necessary to consider the effect of nuclear exchange on each term

in equation (F. 1 ). We will simplify things somewhat by focussing on homonuclear diatomic

molecules (this discussion would be irrelevant for heteronuclear diatomics since they do not

possess identical nuclei). Dealing with the electronic wavefunction ﬁrst, the symmetry with

respect to nuclear exchange depends on the symmetry of the electronic wavefunction. For

a totally symmetric (



) electronic state, the electronic wavefunction is totally symmetric

with respect to nuclear exchange. However, for other electronic states the wavefunction may

be antisymmetric, e.g.



−

.Wewill concentrate on the totally symmetric case but the

arguments below will differ for the antisymmetric electronic states. In a diatomic molecule

the vibrational wavefunction is always totally symmetric with respect to the exchange of

nuclei since the wavefunction depends only on the separation of the nuclei, and this is

269

270 Appendix F

unchanged by a permutation of the nuclei. Note that in polyatomic molecules the vibrational

wavefunction is not always totally symmetric with respect to the exchange of identical

nuclei.

F. 1 Fermionic nuclei

If the identical nuclei are fermions, the overall molecular wavefunction must be antisym-

metric with respect to nuclear exchange. In a diatomic molecule in a totally symmetric

electronic state only the rotational and nuclear spin states need to be considered to deter-

mine the symmetry of the overall wavefunction. In this book we have not discussed the

explicit form of the rotational wavefunctions of molecules. However, it can be shown that

for diatomic molecules the symmetry of ψ

for the interchange of identical nuclei is (−1)

where J is the rotational quantum number. Thus rotational levels with even J are sym-

metric and those with odd J are antisymmetric. Consequently, for the product ψ

be antisymmetric, a symmetric ψ

must be associated with a rotational level having odd

J,whereas an antisymmetric ψ

combines with even J levels. It can be shown that, for

different nuclear spins, the number of symmetric and antisymmetric nuclear spin states is

given by the following formulae:

symm

= (2I + 1)(I + 1) (F.2)

antisymm

= (2I + 1)I (F.3)

The nuclear spins I of selected nuclei are given in Table F. 1 .For a nuclear spin of I =

,as

found for example in each nucleus in H

, there are four possible nuclear spin wavefunctions,

three of which are symmetric and one which is antisymmetric, i.e. there are three times as

many symmetric as antisymmetric states (cf. the spin wavefunctions for two electrons shown

in the previous appendix). These are known as ortho and para states, respectively. The ortho

states are associated with odd J values, whereas the para states are associated with even

J.Transitions originating from these states will have corresponding differences in their

intensities due to the 3:1 alternation in statistical weights.

F. 2 Bosonic nuclei

For nuclei with integer spins, the total wavefunction must be symmetric with respect to

exchange of identical nuclei. If for example I = 1, there are six symmetric and three anti-

symmetric nuclear spin wavefunctions. The symmetric nuclear spin wavefunctions combine

with even J states and will have approximately twice the population of odd J states. As

above, these differences in population will be reﬂected in the intensities of transitions orig-

inating in these states.

If we consider a molecule with two identical nuclei possessing zero spin, such as in the

molecule, antisymmetric nuclear spin states will be missing. The ground electronic

Nuclear spin statistics

271

Table F.1 Nuclear spin quantum

numbers for some selected nuclei

Nucleus I

H (D) 1

H (T)

127

state of C



and so is symmetric with respect to nuclear exchange. Since

C nuclei

are bosons, we have the seemingly bizarre but true situation that the molecule can only exist

in rotational energy levels with even J.Interms of spectroscopy, this will mean that every

other rotational line in the spectrum will be missing. The linear triatomic molecule C

also

behaves in this manner and the role of nuclear spin statistics in interpreting the rotational

structure of this molecule was discussed in Chapter 16.

Appendix G

Coupling of angular momenta:

Hund’s coupling cases

The discussion of angular momentum coupling in Appendix C focussed on electronic

(orbital and spin) angular momenta. Other types of angular momenta may be present in

molecules and their coupling to electronic angular momenta can have an important impact

in spectroscopy. In this appendix rotational angular momentum is added to the pot and its

interaction with electronic angular momenta is considered. The discussion is restricted to

linear molecules, and several limiting cases, known as Hund’s coupling cases, are brieﬂy

described.

G.1 Hund’s case (a)

Hund’s case (a) coupling builds upon the orbital + spin coupling already described in

Appendix C. The orbital angular momenta in a molecule are assumed to be coupled to the

internuclear axis by an electrostatic interaction and spin–orbit coupling leads to the spin

angular momenta also precessing around the same axis. However, the spin–orbit coupling

is not too strong to blur the distinction between orbital and spin angular momenta. Rotation

in a linear molecule leads to rotational angular momentum and yields a vector R that is

oriented perpendicular to the internuclear axis, as shown in Figure G.1.

In Hund’s case (a) it is assumed that the interaction between the electronic and rotational

angular momenta is weak, and hence the former (the orbital angular momentum L and the

spin angular momentum S) continue to precess rapidly around the internuclear axis with

projections whose sum is equal to  (=  + ). The total angular momentum J, electronic

+ rotational, is the vector sum of R and Ω. The vectors R and Ω precess about vector J.

In Hund’s case (a) the quantum numbers J, , , S, and  are all well deﬁned. We could

also add a quantum number to deﬁne the rotational angular momentum but this would be

redundant if we already know J and the electronic angular momentum quantum numbers.

Since  is the quantum number representing the projection of J on the internuclear axis,

the minimum possible value of J is . The allowed values of J are therefore ,  + 1,

 + 2,  + 3, etc. If the number of unpaired electrons is odd then  will be a half-integer

quantum number and therefore J also has half-integer values only.

272

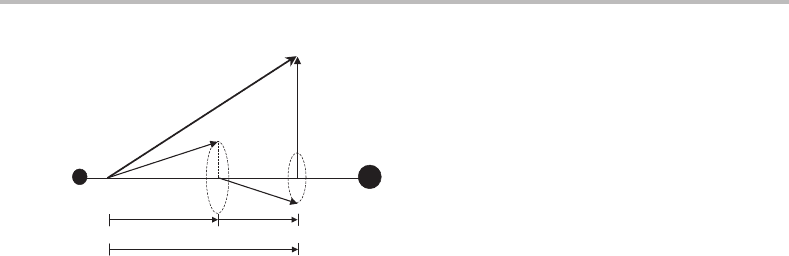
Coupling of angular momenta: Hund’s coupling cases

273

Ω

Figure G.1 Illustration of Hund’s case (a) coupling. The strong axial electric ﬁeld along the internu-

clear axis causes the total electron orbital (L) and spin (S) angular momenta to precess rapidly about

the internuclear axis. The components of these angular momenta along the internuclear axis are well

deﬁned, giving quantum number , and this couples with the rotational angular momentum of the

molecule (R)toform a resultant, J.

The rotational energy levels of Hund’s case (a) molecules can be derived by analogy

with symmetric top rotational energy level formulae. The angular momentum about the

internuclear axis, denoted by quantum number ,isequivalent to the projection of rotational

angular momentum, K,inaprolate symmetric top (see equation 6.15), and so we can write

J,

= BJ(J + 1) + (A − B)

(G.1)

A is inversely related to the moment of inertia of the electrons and by deﬁnition is therefore

very large. The A

term can in fact be ignored since it is a purely electronic term that

contributes equally to all rotational energy levels, leaving the expression

J,

= B[J (J + 1) −

] (G.2)

Molecules showing Hund’s case (a) behaviour possess orbital angular momentum. The

rotational energy levels of a molecule in a

 state are shown in Figure G.2 as an illustration.

In this example three spin–orbit sub-states arise whose separation depends on the magnitude

of the spin–orbit coupling. Notice that the lowest rotational level in each sub-state has the

value  for that sub-state.

The basis of Hund’s case (a) coupling is that the orbital and spin angular momenta

remain ﬁrmly coupled to the internuclear axis even when the molecule rotates. This is

a good approximation but in practice the rotation does induce some uncoupling and this

growsinmagnitude as the speed of rotation increases, i.e. as J increases. This uncoupling

removes the two-fold degeneracy in  and is therefore known as -doubling. This splitting

of each rotational level is shown in Figure G.2,but is exaggerated and in practice the

effect of -doubling can only be resolved in high resolution experiments. Notice that

the two components for a given J can be distinguished by an additional symmetry label,

the parity of the energy level (±). This refers to the symmetry with respect to inversion

(switching coordinates (x, y, z)to(−x,−y,−z)) of all particles in a laboratory-ﬁxed axis

system, i.e. one not attached to the molecule. We shall not consider this any further except

to say that it is helpful in the determination of transition selection rules (for example see

274 Appendix G

Figure G.2 Rotational energy levels of a molecule in a

 electronic state satisfying Hund’s case

(a) coupling. Spin–orbit coupling splits the

 state into the spin–orbit components



, and



,where the subscript refers to the quantum number . Each rotational level within a particular

spin–orbit component is split into a doublet due to -doubling, but the size of this effect is much

exaggerated in this diagram.

Chapter 24). More details can be found in the books listed in the Further Reading section

at the end of this appendix.

G.2 Hund’s case (b)

The premise of Hund’s case (b) is that the spin–orbit coupling is no longer strong enough

to tie the precession of S to the internuclear axis. This most commonly occurs when  = 0,

but it is also known in molecules with  =0 under certain conditions (see below). Assuming

 = 0, only the spin and rotational angular momenta remain and these couple together and

precess around the resultant J. More generally, we have the situation shown in Figure G.3,

wherethe possibility of a non-zero Λ has been included. The precession of the orbital angular

momentum around the internuclear axis remains rapid and the total angular momentum

excluding electron spin, designated as vector N,isthen given by R + Λ.Aweak interaction

then occurs between N and S and these vectors precess slowly about the total angular

momentum vector J.

The quantum numbers used to deﬁne Hund’s case (b) states are J, N, , and S. Notice

that  is no longer a good quantum number in the Hund’s case (b) limit, since precession

of the electron spin is no longer tied to the internuclear axis. If  = 0 then the lowest value