Ellis A.M., Feher M., Wright T. Electronic and Photoelectron Spectroscopy: Fundamentals and Case Studies
Подождите немного. Документ загружается.


The principles of point group symmetry and group theory
255
block-diagonalized into a 2×2,a5×5, and another 2×2 matrix:
a
11
a
12
.
.
. 00000
.
.
.0 0
.
.
.
.
.
.
a
21
a
22
.
.
. 00000
.
.
.0 0
.
.
.
.
.
.
00
.
.
. a
33
a
34
a
35
a
36
a
37
.
.
.0 0
.
.
.
.
.
.
00
.
.
. a
43
a
44
a
45
a
46
a
47
.
.
.0 0
.
.
.
.
.
.
00
.
.
. a
53
a
54
a
55
a
56
a
57
.
.
.0 0
.
.
.
.
.
.
00
.
.
. a
63
a
64
a
65
a
66
a
67
.
.
.0 0
.
.
.
.
.
.
00
.
.
. a
73
a
74
a
75
a
76
a
77
.
.
.0 0
.
.
.
.
.
.
.
.
.
.
.
.
00
.
.
. 00000
.
.
. a
88
a
89
.
.
.
.
.
.
00
.
.
. 00000
.
.
. a
98
a
99
If no transformation exists that brings the representation to a block-diagonal form, it is said
to be irreducible.
Unlike the arbitrary matrix representations above, irreducible representations are unique:
they are the simplest representations of the symmetry group. It is, however, often rather
difficult to find the appropriate similarity transformation to bring the matrix representation
to an irreducible form. Luckily, as will be shown later, it is usually sufficient to use the
characters of the representation, where the character is defined as the trace of the corre-
sponding matrix (i.e. the sum of its diagonal elements). Dealing with characters is much
simpler than dealing with matrix representations, and these can be collected together into
tables for general use.
There are five important rules that form the basis of the derivation of character tables.
The reader who is only interested in the use of character tables can simply skip these.
(i) The number of irreducible representations of a group equals the number of classes in
the group.
(ii) The order of the group, h,isdetermined by the dimension of its irreducible represen-
tations, i.e.
h =
i
l
2
i
(D.4)
where l
i
is the dimension of the ith irreducible representation.
(iii) The sum of the squares of the characters in any irreducible representation is equal to
the order of the group,
h =
R
[χ
i
(R)]
2
(D.5)
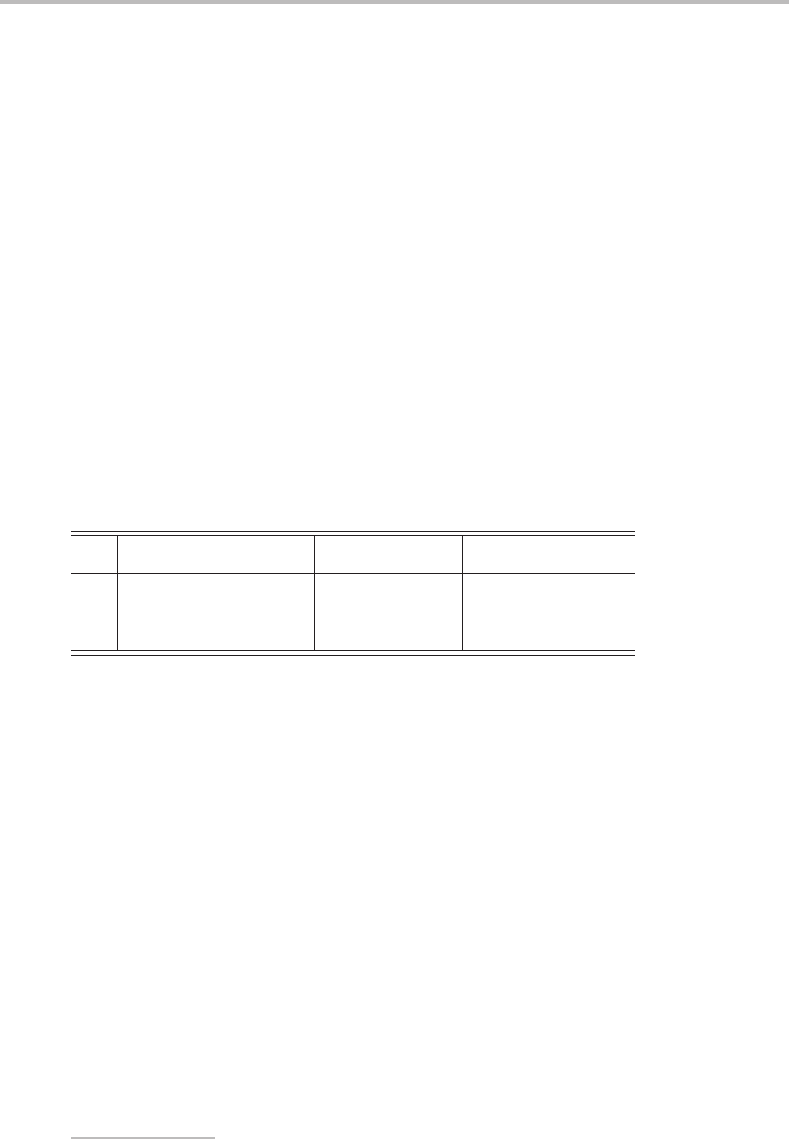
256 Appendix D
where χ
i
(R)isthe character (trace of the matrix) representing the Rth symmetry oper-
ation in the ith irreducible representation.
(iv) In any irreducible representation the characters that belong to symmetry operations in
the same class are identical.
(v) The following expression holds for the characters of two different irreducible repre-
sentations (orthogonality relation):
R
χ
i
(R)χ
j
(R) = 0, where i = j (D.6)
D.5 Character tables
The properties of point groups can be summarized using character tables. Character tables
list the possible symmetry operations for a given point group along with the irreducible
representations and their characters. The character tables for the most important point
groups can be found at the end of this appendix.
The way character tables are arranged is illustrated below for the C
3v
point group.
C
3v
E 2C
3
3σ
v
A
1
11 1z x
2
+ y
2
, z
2
A
2
11−1 R
z
E 2 −10(x, y), (R
x
, R
y
)(x
2
− y
2
, xy), (xz, yz)
This character table consists of four sections, separated above by double lines (optional). In
the leftmost column, beneath the point group symbol, are the irreducible representations.
These are sometimes also called symmetry species, or simply the symmetry. The uppermost
irreducible representation is always the totally symmetric one, for which all characters are
equal to 1. These characters can be seen to the right of the A
1
label.
Conventionally, the symbols for irreducible representations are determined in the fol-
lowing way. One-dimensional representations are marked with the letters A or B,two-
dimensional representations by E, three-dimensional ones usually with the letter T.
1
For
one-dimensional representations, the letter A is used when the character for the rotation
around the principal axis is +1 (i.e. when it is symmetric for this transformation) and B
when this character is −1. The symmetry with respect to the rotation around the axis per-
pendicular to the principal axis (or in its absence reflection in the σ
v
plane) is shown as a
subscript, 1 for the symmetric and 2 for the antisymmetric representation. Reflections in
the σ
h
plane are designated with a prime (symmetric) or double prime (antisymmetric). The
subscripts g and u denote the symmetric or antisymmetric nature of the representation with
respect to inversion.
1
Exceptions to this are the linear molecule point groups D
∞h
and C
∞v
,where labels such as σ and π are preferred
over A and E. This is discussed again later in the appendix.

The principles of point group symmetry and group theory
257
The second section of the C
3v
character table gives the character for each irreducible rep-
resentation and for each class of symmetry operations. It is useful to note that the character
for the identity operation is equal to the dimension of the irreducible representation.
The final two columns provide information about the symmetries of cartesian vectors
(x, y, z),
2
products of these vectors, and rotations about the cartesian axes (R
x
, R
y
, and R
z
).
This information is useful for determining spectroscopic selection rules. For example, the z
coordinate axis in the C
3v
point group transforms like the totally symmetric (A
1
)irreducible
representation, because it is unaffected by the operations of the group. R
z
also appears on
its own and transforms as the A
2
irreducible representation. In contrast to these, x and y
(and similarly R
x
and R
y
) jointly form a representation. This arises because, after the C
3
operation is performed, the resulting vector will contain both x and y components. As a
result, x and y are inseparable in this respect, and so they jointly form a representation and
transform as the E irreducible representation.
D.6 Reducible representations, direct products, and direct product tables
There are many occasions in spectroscopy when it is necessary to multiply irreducible
representations, or in the language of group theory, calculate their direct products. The
direct product is obtained by multiplying the characters for each symmetry element. The
resulting representations are often reducible. It can be proved that the number of times (a
i
)
an irreducible representation occurs within a reducible one can be determined using the
following formula:
a
i
=
1
h
R
χ
red
(R)χ
i
(R) (D.7)
where χ
red
(R)isthe character of the reducible representation corresponding to operation
R, and χ
i
(R)isthe character of the irreducible representation. The summation is over all
symmetry operations and h is the order of the group.
This rule can be illustrated by determining the direct product of the E species with itself
within the C
3v
point group, i.e. E ⊗ E.Asthe characters for the E species are 2, −1, and 0,
the characters of the direct product will be =4, 1 and 0. This is a reducible representation
that can be decomposed to irreducible representations using the formula above, yielding
a
A
1
=
1
6
[1(1)(4) + 2(1)(1) +3(1)(0)] = 1
a
A
2
=
1
6
[1(1)(4) + 2(1)(1) +3(−1)(0)] = 1
a
E
=
1
6
[1(2)(4) + 2(−1)(1) +3(0)(0)] = 1
2
The symmetry of a cartesian vector is the same as the symmetry of the corresponding cartesian axis. For example,
the x axis has both positive and negative regions and any rotation about this axis will leave these unmoved. On the
other hand, a C
2
rotation about an axis perpendicular to the x axis and passing through the origin will transform x
into −x, and vice versa. In other words, the x axis in this instance will be antisymmetric with respect to C
2
. Thus
symmetry operations can be applied to cartesian vectors in a manner identical to their application to molecules.

258 Appendix D
Table D.4 Direct product table for point groups C
2
, C
2v
, C
2h
, C
3
, C
3v
,
C
3h
, D
3
, D
3h
, D
3d
, C
6
, C
6v
, C
6h
, D
6
, S
6
, D
6h
A
1
A
2
B
1
B
2
E
1
E
2
A
1
A
1
A
2
B
1
B
2
E
1
E
2
A
2
A
1
B
2
B
1
E
1
E
2
B
1
A
1
A
2
E
2
E
1
B
2
A
1
E
2
E
1
E
1
A
1
+ [A
2
] + E
2
B
1
+ B
2
+ E
1
E
2
A
1
+ [A
2
] + E
2
Table D.5 Direct product table for point groups T, T
h
,T
d
,O,O
h
A
1
A
2
ET
1
T
2
A
1
A
1
A
2
ET
1
T
2
A
2
A
1
ET
2
T
1
E A
1
+ [A
2
] + ET
1
+ T
2
T
1
+ T
2
T
1
A
1
+ E + [T
1
] + T
2
A
2
+ E + T
1
+ T
2
T
2
A
1
+ E + [T
1
] + T
2
Table D.6 Direct product table for point groups C
∞v
and D
∞h
Σ
+
Σ
−
Π∆
Σ
+
+
−
Σ
−
+
Π
+
+ [
−
] + +
∆
+
+ [
−
] +
Note that the number of symmetry operations in each class needs to be considered, and
these are the first numbers in each term inside the square brackets. The result is that the
direct product E ⊗ E can be reduced to A
1
+ A
2
+ E. That this finding is correct can be
confirmed by adding up the characters of the three irreducible representations, which will
yield the original reducible representation.
Fortunately, it is not necessary to use (D.7)every time direct products of irreducible
representations are required. Instead, direct product tables are available, which allow the
task to be carried out quickly and easily. Direct product tables often prove themselves to be
just as useful in spectroscopy as character tables, and it is important to be comfortable with
their use. Three direct product tables are, D.1, D.2, and D.3, are shown above, covering a
wide range of point groups.
Interpretation and use of the direct product tables requires a little care. First, notice that
each table applies to a number of different point groups. In some cases the irreducible
representations in the table do not correspond exactly to those of one of the listed point

The principles of point group symmetry and group theory
259
groups. For example, the four irreducible representations of the C
2h
point group are A
g
,
B
g
, A
u
, and B
u
. None of these appears in Table D.4, and yet this is the direct product table
that is supposed to apply to the C
2h
point group. To find the direct products we do the
following. First, if the irreducible representations of the point group have no numerical
subscripts, the corresponding subscripts in the direct product table are ignored. Second, if
the irreducible representations have u or g subscripts, or they have a
or
superscript, the
following additional product rules apply:
r
Forgand u subscripts:
g
⊗
g
=
g
,
g
⊗
u
=
u
,
u
⊗
g
=
u
, and
u
⊗
u
=
g
r
For
and
superscripts:
⊗
=
,
⊗
=
,
⊗
=
, and
⊗
=
Thus, for example, if the direct product B
g
⊗ A
u
is required for the C
2h
point group, the
above rules show that B
g
⊗ A
u
= B
u
.Asanother example, the E
1
⊗ E
1
direct product in
the C
6
point group is found to be A
1
+ [A
2
] + E
2
. The significance of the square bracket
around A
2
will be seen later.
It is sometimes necessary to extend the concept of direct products to a higher number of
terms. As an example, a triple direct product can be calculated by taking the direct product
of any pair of representations, and then using the result to calculate its direct product with
the third. This operation is commutative, so the order of multiplication does not matter.
Triple direct products are particularly useful in the discussion of spectroscopic selection
rules (see Section 7.1.2).
There are certain simple rules regarding direct products that are helpful to remember
and which can readily be checked by consulting the direct product tables.
r
The direct product of the totally symmetric irreducible representation with a non-
totally symmetric representation gives the non-totally symmetric representation (as all
characters of the totally symmetric species are 1).
r
The direct product of any one-dimensional irreducible representation with itself gives
the totally symmetric representation.
r
The direct product of a higher-dimensional species with itself will be reducible and
always includes the totally symmetric irreducible representation.
D.7 Cyclic and linear groups
The discussion above shows how to interpret, and use, the character tables for most point
groups. However, there are two types of groups that are a little more complicated. One of
these falls into the category of the so-called cyclic groups. They are called cyclic because all
their symmetry elements can be generated from different powers of one of their elements.
Cyclic groups can easily be recognized from their character tables, as the characters of
two-dimensional species contain a function and its complex conjugate. Examples include
the groups C
3
, C
5
, C
3h
, and many others. The other category that presents difficulties at
first sight is the linear molecule point groups C
∞v
and D
∞h
.
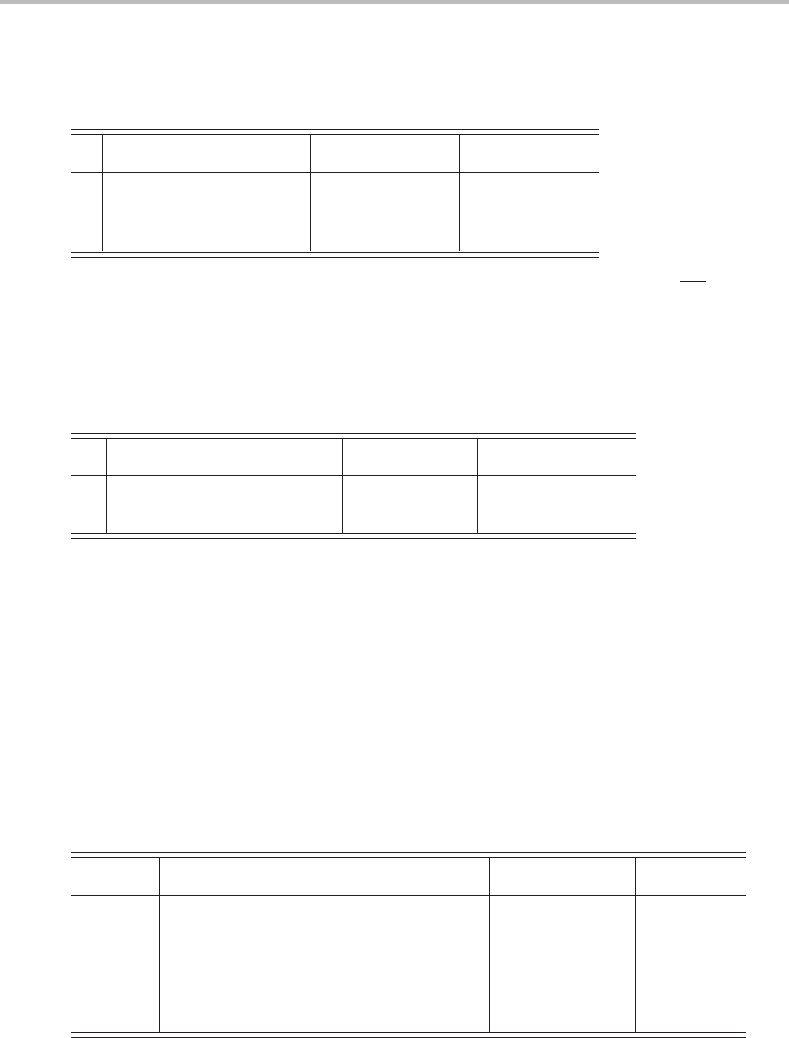
260 Appendix D
Consider the C
3
point group as an example of a cyclic group. The character table for this
group is as follows:
C
3
EC
3
C
2
3
ε = exp(2πi/3)
A 11 1z, R
z
x
2
+ y
2
, z
2
E
%
1
1
%
ε
ε
∗
ε
ε
∗
&
(x , y)(R
x
, R
y
)
(x
2
− y
2
, xy)
(yz, xz)
In this table, the symbol ε stands for the quantity exp(2πi/3), where i =
√
−1, and ε
∗
is
the complex conjugate of ε, i.e. exp(−2πi/3). It can be shown that, for the purposes of
many physical applications, the two rows belonging to the E representation can be added,
so that the resulting row only contains real numbers. When this is done the following table
is obtained:
C
3
EC
3
C
2
3
A 11 1 z, R
z
x
2
+ y
2
, z
2
E 22cos 2π/32cos 2π/3(x, y), (R
x
, R
y
)(x
2
− y
2
, xy), (xz, yz)
which can be used like any other character table. As an example, we can try to reduce
the direct product E ⊗ E.Asthe characters for the E representation are 2, 2 cos 2π/3, and
2 cos 2π/3, the characters of the direct product will be =4, 4 cos
2
2π/3, and 4 cos
2
2π/3.
It can be shown by applying well-known trigonometric relationships, namely sin
2
x + cos
2
x
= 1 and cos 2x = cos
2
x − sin
2
x, that the characters of the direct product are equal to
= 4, 2 + 2 cos 2π/3, and 2 + 2 cos 2π/3. It is easy to see that this is simply the sum of
three species, i.e. E ⊗ E = 2A + E.
The character tables for linear molecules, C
∞ v
and D
∞ h
, are also somewhat peculiar at
first sight. These two groups differ in the existence of the centre of symmetry as a symmetry
element. As an example, the character table for the point group C
∞ v
is shown below.
C
∞v
E 2C
φ
∞
... ∞σ
v
A
1
≡
+
11 ... 1 z x
2
+ y
2
, z
2
A
2
≡
−
11 ... −1 R
z
E
1
≡ 22cos φ ... 0 (x, y), (R
x
, R
y
)(xz, yz)
E
2
≡ 22cos 2φ ... 0 (x
2
− y
2
, xy)
E
3
≡ 22cos 3φ ... 0
... ... ... ... ...
First, there is an infinite number of classes because rotation about any angle φ about the C
∞
axis is a symmetry operation and each of these C
φ
∞
elements belongs to a different class.
Similarly, there is an infinite number of σ
v
planes. The consequence of an infinite number
of symmetry elements is that there is also an infinite number of irreducible representations.
The labelling of these is often slightly confusing. On the one hand, they are sometimes
named according to the conventions described above, i.e. A
1
, A
2
, E
1
, E
2
, etc. More usually

The principles of point group symmetry and group theory
261
they are labelled according to the convention introduced in electronic structure theory to
describe electronic states of linear molecules, namely , , , , etc. As described in
Sections 4.2.2 and 4.2.3,inelectronic states these labels correspond to different values of
the angular momentum quantum number .
The direct products of irreducible representations in linear groups can be calculated in a
similar manner to other point groups. Taking
−
⊗ as an example, the characters of the
direct product are = 2, 2 cos φ,...,0,i.e.
−
⊗ = .Trigonometric relationships
need to be invoked for the direct products of two- or higher-dimensional representations.
Forexample, the characters of the direct product ⊗ are = 4, 4 cos
2
φ ...,0.Using
the above relationships it can be shown that 4 cos
2
φ = 2 + 2 cos 2φ, and hence ⊗ =
+
+
+
−
.Inpractice such manipulations are not necessary and direct products can
be obtained simply by inspecting Table D.6.
D.8 Symmetrized and antisymmetrized products
In the description of spectroscopic states it is sometimes necessary to invoke the sym-
metrized and antisymmetrized product of two functions, instead of simply taking their
product. For functions f
i
and f
j
, the symmetrized product is
1
/
2
(f
i
f
j
+ f
j
f
i
), whereas the anti-
symmetrized product is
1
/
2
(f
i
f
j
−f
j
f
i
). It can be proved that both of these products are reducible
representations of the point group. In many examples, the antisymmetrized product simply
vanishes.
Symmetrized and antisymmetrized products have special importance when the electronic
state is derived for two electrons. The resulting electronic state can be obtained from the
direct product of the symmetry species of the molecular orbitals. Careful consideration of
the Pauli principle is required if the electrons reside in degenerate orbitals and this is a topic
considered in more detail in the next appendix.Indirect product tables antisymmetrized
direct products are displayed in square brackets.
Further reading
Good introductory accounts of symmetry and point group theory in chemical and spectro-
scopic applications can be found in the following books:
Group Theory and Chemistry,D.M.Bishop, New York, Dover, 1993.
Molecular Symmetry and Group Theory,R.L.Carter, New York, Wiley, 1998.
Chemical Applications of Group Theory,F.A.Cotton, New York, Wiley, 1990.
Molecular Symmetry and Group Theory: A Programmed Introduction to Chemical Appli-
cations,A.Vincent, Chichester, Wiley, 2001.
More advanced aspects, most notably consideration of flexible molecules, which cannot be
treated adequately by point group theory, can be found in the following books:
Molecular Symmetry and Spectroscopy,P.R.Bunker and P. Jensen, Ottawa, NRC Press,
1998.
Symmetry, Structure and Spectroscopy of Atoms and Molecules,W.J.Harter, New York,
Wiley, 1993.

262 Appendix D
Selected character tables
C
1
E
A 1
C
s
E σ
h
A
11x, y, R
z
x
2
, y
2
, z
2
, xy
A
1 −1 z, R
x
, R
y
yz, xz
C
i
Ei
A
g
11R
x
, R
y
, R
z
x
2
, y
2
, z
2
, xy, xz, yz
A
u
1 −1 x, y, z
C
2
EC
2
A 11z, R
z
x
2
, y
2
, z
2
, xy
B 1 −1 x, y, R
x
, R
y
yz, xz
C
3
EC
3
C
2
3
ε = exp(2πi/3)
A 11 1z, R
z
x
2
+ y
2
, z
2
E
%
1
1
ε
ε
∗
ε
ε
∗
&
(x , y), (R
x
, R
y
)
(x
2
− y
2
, xy)
(yz, xz)
C
4
EC
4
C
2
C
3
4
A 1 111z, R
z
x
2
+ y
2
, z
2
B 1 −11−1 x
2
− y
2
, xy
E
%
1
1
i
−1
−1
−1
−i
i
&
(x , y),
(R
x
, R
y
)
(yz, xz)
C
6
EC
6
C
3
C
2
C
2
3
C
5
6
ε = exp(2πi/6)
A 1 1111 1z, R
z
x
2
+ y
2
, z
2
B 1 −11−11 −1
E
1
%
1
1
ε
ε
∗
−ε
∗
−ε
−1
−1
−ε
−ε
∗
ε
∗
ε
&
(x , y),
(R
x
, R
y
)
(xz, yz)
E
2
%
1
1
−ε
∗
−ε
−ε
−ε
∗
1
1
−ε
∗
−ε
−ε
−ε
∗
&
x
2
− y
2
, xy

The principles of point group symmetry and group theory
263
D
2
EC
2
(z) C
2
(y) C
2
(x)
A 11 1 1 x
2
, y
2
, z
2
B
1
11−1 −1 z, R
z
xy
B
2
1 −11−1 y, R
y
xz
B
3
1 −1 −11x, R
x
yz
C
2v
EC
2
(z) σ
v
(xz) σ
v
(yz)
A
1
11 1 1 z x
2
, y
2
, z
2
A
2
11−1 −1 R
z
xy
B
1
1 −11−1 x, R
y
xz
B
2
1 −1 −11y, R
x
yz
C
3v
E 2C
3
(z)3σ
v
A
1
11 1z x
2
+ y
2
, z
2
A
2
11 −1 R
z
E 2 −10(x, y), (R
x
, R
y
)(x
2
− y
2
, xy), (xz, yz)
C
4v
E 2C
4
C
2
2σ
v
2σ
d
A
1
11 11 1z x
2
+ y
2
, z
2
A
2
11 1−1 −1 R
z
B
1
1 −111−1 x
2
− y
2
B
2
1 −11−11 xy
E 20−20 0(x, y), (R
x
, R
y
)(xz, yz)
C
2h
EC
2
i σ
h
A
g
1 111R
z
x
2
, y
2
, z
2
, xy
B
g
1 −11−1 R
x
, R
y
xz, yz
A
u
11−1 −1 z
B
u
1 −1 −11x, y
D
2h
EC
2
(z) C
2
(y) C
2
(x) i σ (xy) σ (xz) σ (yz)
A
g
11 111111 x
2
, y
2
,z
2
B
1g
11−1 −111−1 −1 R
z
xy
B
2g
1 −11−11−11−1 R
y
xz
B
3g
1 −1 −111−1 −11R
x
yz
A
u
11 1 1−1 −1 −1 −1
B
1u
11−1 −1 −1 −111z
B
2u
1 −11−1 −11 −11y
B
3u
1 −1 −11−11 1−1 x
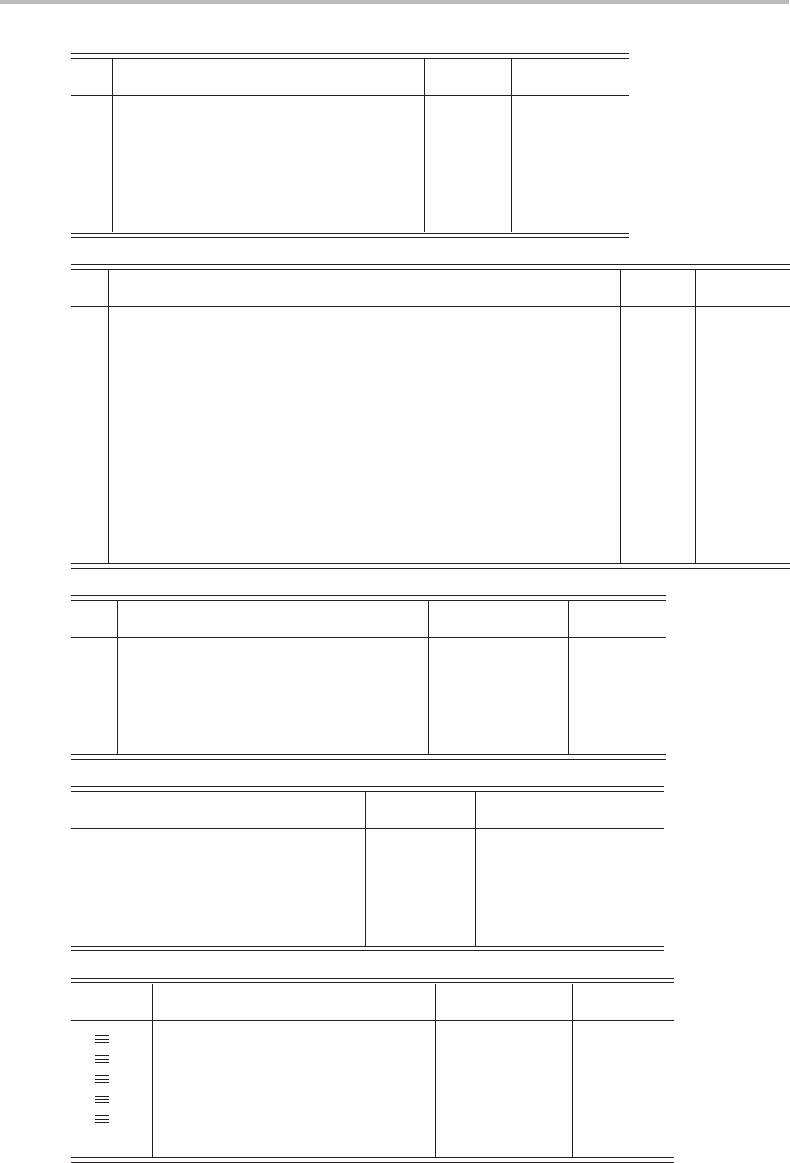
264 Appendix D
D
3h
E 2C
3
3C
2
σ
h
2S
3
3σ
v
A
1
1 11111 x
2
+ y
2
, z
2
A
2
11−111−1 R
z
,(x, y)(x
2
− y
2
, xy)
E
2 −102−10
A
1
11 1−1 −1 −1 z,(R
x
, R
y
)(xz, yz)
A
2
11−1 −1 −11
E
2 −10−210
D
6h
E 2C
6
2C
3
C
2
3C
2
C
2
i 2S
3
2S
6
σ
h
3σ
d
3σ
v
A
1g
1 11111111111 x
2
+ y
2
, z
2
A
2g
1 111−1 −11111−1 −1 R
z
B
1g
1 −11−11−11−11−11−1
B
2g
1 −11−1 −111−11−1 −11
E
1g
21−1 −20 021−1 −20 0(R
x
, R
y
) (xz, yz)
E
2g
2 −1 −12002−1 −120 0 (x
2
− y
2
, xy)
A
1u
1 11111−1 −1 −1 −1 −1 −1
A
2u
1 111−1 −1 −1 −1 −1 −11 1z
B
1u
1 −11−11−1 −11−11−11
B
2u
1 −11−1 −11−11−111−1
E
1u
21−1 −20 0−2 −1120 0(x, y)
E
2u
2 −1 −1200−21 1−20 0
D
2d
E 2S
4
C
2
2C
2
2σ
d
A
1
1111 1 x
2
+ y
2
, z
2
A
2
111−1 −1 R
z
B
1
1 −111−1 x
2
− y
2
B
2
1 −11−11zxy
E
20−20 0(x, y), (R
x
, R
y
) (xz, yz)
T
d
E 8C
3
3C
2
6S
4
6σ
d
A
1
1 1111 x
2
+ y
2
+ z
2
A
2
11 1−1 −1
E 2 −1200 (2z
2
− x
2
− y
2
, x
2
−y
2
)
T
1
30−11−1(R
x
, R
y
, R
z
)
T
2
30−1 −11(x, y, z) (xy, xz, yz)
C
∞v
E 2C
φ
∞
... ∞σ
v
A
1
+
11 ... 1 zx
2
+ y
2
, z
2
A
2
−
11 ... −1 R
z
E
1
22cos φ ... 0 (x, y), (R
x
, R
y
) (xz, yz)
E
2
22cos 2φ ... 0 (x
2
− y
2
, xy)
E
3
22cos 3φ ... 0
... ... ... ... ...
