El-Hawary M.E. Electrical Energy Systems

194

Figure 6.4 Torque-Slip Characteristics for Induction Motor.

2

1

3

T

s

X

s

R

s

R

V

T

+













=

ω

The slip at which maximum torque occurs as

T

X

R

s

T

2

max

= (6.15)

The value of maximum torque is

Ts

X

V

T

ω

2

3

2

1

max

= (6.16)

The torque-slip variations are shown in Figure 6.4.

Example 6.3

The resistance and reactance of a squirrel-cage induction motor rotor at

standstill are 0.125 ohm per phase and 0.75 ohm per phase, respectively.

Assuming a transformer ratio of unity, from the eight-pole stator having a phase

voltage of 120 V at 60 Hz to the rotor secondary, calculate the following:

A. rotor starting current per phase, and

B. the value of slip producing maximum torque.

Solution

A. At starting, s = 1:

195

A538.80823.157

75.0125.0

120

−∠=

+

=

j

I

r

B.

1667.0

75.0

125.0

max

===

T

r

X

R

s

T

The following script implements Example 6.3 in MATLAB



:

The results obtained from MATLAB



are as follows:

Example 6.4

The full-load slip of a squirrel-cage induction motor is 0.05, and the starting

current is five times the full-load current. Neglecting the stator core and copper

losses as well as the rotational losses, obtain:

A. the ratio of starting torque (st) to the full-load torque (fld), and

% Example 6-3

% A squirrel cage induction motor

Rr=0.125; % ohm

XT=0.75; % ohm

V=120; % Volt

f=60; % Hz

% A. Rotor starting current per phase

% At starting s=1

Ir= V/(Rr+i*XT)

abs(Ir)

angle(Ir)*180/pi

% B. The value of slip producing

maximum torque

s_maxT=Rr/XT

EDU»

Ir = 2.5946e+001 - 1.5568e+002I

ans = 157.8230

ans = -80.5377

s_maxT = 0.1667

196

B. the ratio of maximum (max) to full-load torque and the

corresponding slip.

Solution

s

fld

= 0.05 and I

st

= 5I

fld

2

22

2

fld

st

)5(

05.0

=

+













=













T

XR

X

R

I

This gives

25.0

375

24

2

≅=

T

X

R

A.

()

25.1

1

05.0

)5(

3

2

st

fld

2

fld

2

st

fld

st

2

==













=

s

I

T

s

RI

T

s

r

ω

B.

()













+

=

+













=

+

























=













=

==

2

1)5(

25.0

05.0

2

1

2

25.0

2

fld

max

fld

2

fld

2

max

fld

max

fld

2

fld

2

max

fld

max

2

max

s

X

s

R

s

I

T

X

R

s

T

Thus,

197

6.2

fld

max

=

T

The following script implements Example 6.4 in MATLAB



:

The results obtained from MATLAB



are as follows:

% Example 6-4

% A scuirrel cage induction motor

sfld=0.05;

sst=1;

% Ist=5*Ifld;

% ratio1=Ist/Ifld=5

ratio1=5;

%

(ratio1)^2=((R2/sfld)^2+(XT)^2)/(R2^2+(

XT)^2)

% (R2/XT)^2*((1/sfld)^2-

ratio1^2)=ratio1^2-1

% ratio2=R2/XT

f=[((1/sfld)^2-ratio1^2) 0 -(ratio1^2-

1)]

ratio2=roots(f);

ratio2=ratio2(1)

% A. T=3*Ir^2*R2/(sfld*ws)

% ratio3=Tst/Tfld

ratio3=ratio1^2*(sfld/sst)

% B.

s_maxT=ratio2

%Tmax/Tfld=(Imax/Ifld)^2*(sfld/s_maxT)

%=(sfld/s_maxT)*((R2/sfld)^2+XT^2)/(2*X

T^2)

%

(Tmax/Tfld)=(sfld/s_maxT)*((s_maxT/sfld

)^2+1)/2

% ratio4=Tmax/Tfld

ratio4=(sfld/s_maxT)*((s_maxT/sfld)^2+1

)/2

EDU»

f = 375 0 -24

ratio2 = 0.2530

ratio3 = 1.2500

s_maxT = 0.2530

ratio4 = 2.6286

198

6.4 CLASSIFICATION OF INDUCTION MOTORS

Integral-horsepower, three-phase, squirrel-cage motors are available

from manufacturers’ stock in a range of standard ratings up to 200 hp at standard

frequencies, voltages, and speeds. (Larger motors are regarded as special-

purposed.) Several standard designs are available to meet various starting and

running requirements. Representative torque-speed characteristics of four

designs are shown in Figure 6.5. These curves are typical of 1,800 r/min

(synchronous-speed) motors in ratings from 7.5 to 200 hp.

The induction motor meets the requirements of substantially constant-

speed drives. Many motor applications, however, require several speeds or a

continuously adjustable range of speeds. The synchronous speed of an induction

motor can be changed by (1) changing the number of poles, (2) varying the rotor

resistance, or (3) inserting voltages of the appropriate frequency in the rotor

circuits. A discussion of the details of speed control mechanisms is beyond the

scope of this work. A common classification of induction motors is as follows.

Class A

Normal starting torque, normal starting current, low slip. This design

has a low-resistance, single-cage rotor. It provides good running performance at

the expense of starting. The full-load slip is low and the full-load efficiency is

high. The maximum torque usually is over 200 percent of full-load torque and

occurs at a small slip (less than 20 percent). The starting torque at full voltage

Figure 6.5 Typical Torque-Speed Curves for 1,800 r/min General-Purpose Induction Motors.

199

varies form about 200 percent of full-load torque in small motors to about 100

percent in large motors. The high starting current (500 to 800 percent of full-

load current when started at rated voltage) is the disadvantage of this design.

Class B

Normal starting torque, low starting current, low slip. This design has

approximately the same starting torque as the Class A with only 75 percent of

the starting current. The full-load slip and efficiency are good (about the same

as for the Class A). However, it has a slightly decreased power factor and a

lower maximum torque (usually only slightly over 200 percent of full-load

torque being obtainable). This is the commonest design in the 7.5 to 200-hp

range of sizes used for constant-speed drives where starting-torque requirements

are not severe.

Class C

High starting torque, low starting current. This design has a higher

starting torque with low starting current but somewhat lower running efficiency

and higher slip than the Class A and Class B designs.

Class D

High starting torque, high slip. This design produces very high starting

torque at low starting current and high maximum torque at 50 to 100-percent

slip, but runs at a high slip at full load (7 to 11 percent) and consequently has

low running efficiency.

6.5 ROTATING MAGENTIC FIELDS IN SINGLE-PHASE

INDUCTION MOTORS

To understand the operation of common single-phase induction motors,

it is necessary to start by discussing two-phase induction machines. In a true

two-phase machine two stator windings, labeled AA

′

and BB

′

, are placed at 90

°

spatial displacement as shown in Figure 6.6. The voltages

υ

A

and

υ

B

form a set

of balanced two-phase voltages with a 90

°

time (or phase) displacement.

Assuming that the two windings are identical, then the resulting flux

φ

A

and

φ

B

are given by

t

MA

ωφφ

cos

=

(6.17)

tt

MMB

ωφωφφ

sin)90cos(

=−=

$

(6.18)

where

φ

M

is the peak value of the flux. In Figure 6.6(B), the flux

φ

A

is shown to

be at right angles to

φ

B

in space. It is clear that because of Eqs. (6.17) and

(6.18), the phasor relation between

φ

A

and

φ

B

is shown in Figure 6.6(C) with

φ

A

200

taken as the reference phasor.

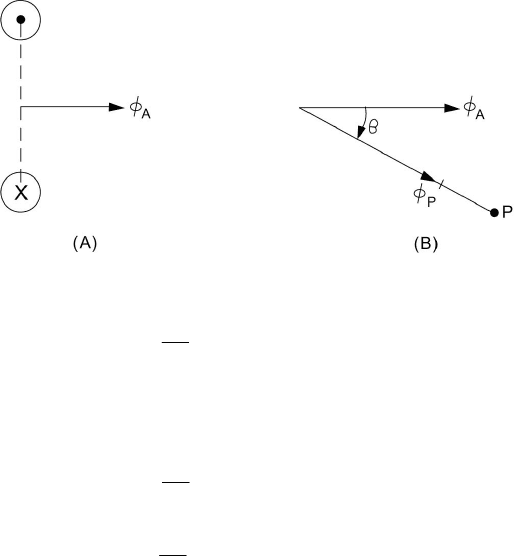
The resultant flux

φ

P

at a point P displaced by a spatial angle

θ

from the

reference is given by

PBPAP

φφφ

+=

where

φ

PA

is the component of

φ

A

along the OP axis and

φ

PB

is the component of

φ

B

along the OP axis, as shown in Figure 6.6(D). Here we have

θφφ

sin

cos

BPB

APA

=

As a result, we have

)sinsincos(cos

θωθωφφ

tt

MP

+=

The relationship above can be written alternatively as

Figure 6.6 Rotating magnetic field in a balanced two-phase stator: (A) winding schematic; (B)

flux orientation; (C) phasor diagram; and (D) space phasor diagram.

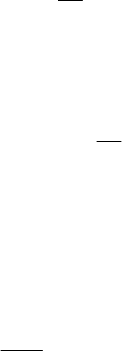
201

)cos( t

MP

ωθφφ

−= (6.19)

The flux at point P is a function of time and the spatial angle

θ

, and has a

constant amplitude

φ

M

. this result is similar to that obtained earlier for the

balanced three-phase induction motor.

The flux

φ

P

can be represented by a phasor

φ

M

that is coincident with

the axis of phase a at t = 0. The value of

φ

P

is

φ

M

cos

θ

at that instant as shown

in Figure 6.7(A). At the instant t = t

1

, the phasor

φ

M

has rotated an angle of

ω

t

1

in the positive direction of

θ

, as shown in Figure 6.7(B).Thevalueof

φ

P

is seen

to be

φ

M

cos (

θ

-

ω

t

1

) at that instant. It is thus clear that the flux waveform is a

rotating field that travels at an angular velocity

ω

in the forward direction of

increase in

θ

.

The result obtained here for a two-phase stator winding set and for a

three-phase stator winding set can be extended to an N-phase system. In this

case the N windings are placed at spatial angles of 2

π

/N and excited by

sinusoidal voltages of time displacement 2

π

/N. Our analysis proceeds as

follows. The flux waveforms are given by













−−=

⋅













−=

=

N

it

N

t

Mi

M

π

ωφφ

π

ωφφ

2

)1(cos

2

cos

2

1

The resultant flux at a point P can be shown to be given by:

∑

=

N

i

PiP

1

φφ

)cos(

2

t

N

M

P

ωθ

φ

−= (6.20)

A rotating magnetic field of constant magnitude will be produced by an

N-phase winding excited by balanced N-phase currents when each phase is

displaced 2

π

/N electrical degrees from the next phase in space.

202

Figure 6.7 Illustrating of forward rotating magnetic field: (A) t = 0; (B) t = t

1

.

In order to understand the operation of a single-phase induction motor,

we consider the configuration shown in Figure 6.8. The stator carries a single-

phase winding and the rotor is of the squirrel-cage type. This configuration

corresponds to a motor that has been brought up to speed, as will be discussed

presently.

Figure 6.8 Schematic of a single-phase induction motor.

Let us now consider a single-phase stator winding as shown in Figure

6.9(A).Theflux

φ

A

is given by

t

MA

ωφφ

cos

=

(6.21)

The flux at point P displaced by angle

θ

from the axis of phase a is clearly given

by

θφφ

cos

AP

=

Using Eq. (6.21), we obtain

203

Figure 6.9 (A) Single-phase winding; (B) the flux at a point P.

)]cos()[cos(

2

tt

M

P

ωθωθ

φ

++−= (6.22)

The flux at point P can therefore be seen to be the sum of two waveforms

φ

f

and

φ

b

given by

)cos(

2

t

M

f

ωθ

φ

−= (6.23)

)cos(

2

t

M

b

ωθ

φ

+= (6.24)

The waveform

φ

f

is of the same form as that obtained in Eq. (6.19), which was

shown to be rotating in the forward direction (increase in

θ

from the axis of

phase a). The only difference between Eqs. (6.23) and (6.21) is that the

amplitude of

φ

f

is half of that of

φ

P

in Eq. (6.21). The subscript f in Eq. (6.23)

signifies the fact that cos (

θ

-

ω

t) is forward rotating wave.

Consider now the waveform

φ

b

of Eq. (6.24). At t = 0, the value of

φ

b

is (

φ

M

/2) cos

θ

and is represented by the phasor (

φ

M

/2), which is coincident with

the axis of phase a as shown in Figure 6.10(a). Note that at t = 0, both

φ

f

and

φ

b

are equal in value. At a time instant t = t

1

, the phasor (

φ

M

/2) is seen to be at

angle

ω

t

1

with the axis of phase a, as shown in Figure 6.9(B). The waveform

φ

b

can therefore be seen to be rotating at an angular velocity

ω

in a direction

opposite to that of

φ

f

and we refer to

φ

b

as a backward-rotating magnetic field.

The subscript (b) in Eq. (6.24) signifies the fact that cos (

θ

+

ω

t) is a backward-

rotating wave.

In a single-phase induction machine there are two magnetic fields

rotating in opposite directions. Each field produces an induction-motor torque

in a direction opposite to the other. If the rotor is at rest, the forward torque is

equal and opposite to the backward torque and the resulting torque is zero. A

El-Hawary M.E. Electrical Energy Systems

Подождите немного. Документ загружается.