Дубинин В.Н., Зинкин С.А. Языки логического программирования в проектировании вычислительных систем и сетей
Подождите немного. Документ загружается.

6 [wait(zero),send(se,re,mes,zero),prec(one)]
7 [receive(se,re,mes,zero),wait(zero),prec(one)]
8 [receive(re,se,ack,zero),prec(one),wait(zero)]
9 [psend(one),prec(one)]
10 [send(se,re,mes,one),wait(one),prec(one)]
11 [ploss,wait(one),prec(one)]
12 [receive(se,re,mes,one),wait(one),prec(one)]
13 [prec(zero),send(re,se,ack,one),wait(one)]
14 [ploss,prec(zero),wait(one)]
15 [wait(one),send(se,re,mes,one),prec(zero)]
16 [receive(se,re,mes,one),wait(one),prec(zero)]
17 [receive(re,se,ack,one),prec(zero),wait(one)]
о дугах ГДС (база данных gds):
0 tsend(zero) 1
1 loss 2
2 repeatm(zero) 1
1 propagate(zero) 3
3 reception(zero) 4
4 loss 5
14 repeatm(one) 15
15 loss 14
5 repeatm(zero) 6
6 loss 5
6 propagate(zero) 7
7 repeata(one) 4
4 propagate(zero) 8
8 recack(zero) 9
15 propagate(one) 16
16 repeata(zero) 13
9 tsend(one) 10
10 loss 11
11 repeatm(one) 10
10 propagate(one) 12
12 reception(one) 13
13 loss 14
13 propagate(one) 17
17 recack(one) 0
На рис.2.12 полученный ГДС представлен в графическом виде. На основе
анализа данного ГДС можно сделать вывод, что соответствующая сетевая
модель является живой, и, следовательно, АБ- протокол свободен от
тупиков.
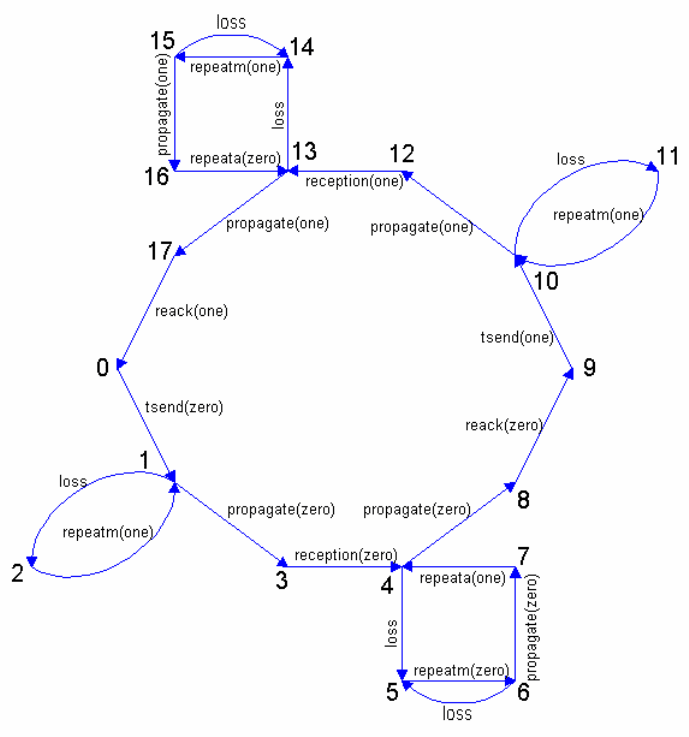
Ðèñ.2.12.Ãðàô äîñòèæèìûõ ñîñòîÿíèé ñåòåâîé ìîäåëè àëüòåðíàòèâíî-áèòîâîãî
ïðîòîêîëà
Типичным примером Р- инварианта является выражение:
М(psend) + M(wait) = 1,
определяющее то, что передатчик находится либо в состоянии psend, либо в
состоянии wait (исключительно).
В полученном ГДС можно выделить следующие последовательности
переходов:
1) (0)
→
tsend(zero), propagate(zero), reception(zero), propagate(zero),
recack(zero)
→
(9).
Данная последовательность соответствует нормальной передаче кадра с
четностью 0.
2) (9)→tsend(one), propagate(one), reception(one), propagate(one),
recack(one)→0.
Данная последовательность соответствует нормальной передаче кадра с
четностью 1.
3) (4)→loss, repeatm(zero), propagate(zero), repeata(zero)→(4).
Данная последовательность соответствует потере подтверждения с
четностью 0 и восстановлению после этой ошибки.
4) (13)→loss, repeatm(zero), propagate(zero), repeata(zero)→(13).
Данная последовательность соответствует потере подтверждения с
четностью 1 и восстановлению после этой ошибки.
5) (1)→loss, repeatm(zero)→(1) и (6)→loss, repeatm(zero)→(6).
Данные последовательности соответствуют потере кадра с четностью 0 и
восстановлению после этой ошибки.
6) (10)→loss, repeatm(zero)→(11) и (15)→loss, repeatm(zero)→(14).
Данные последовательности соответствуют потере кадра с четностью 1 и
восстановлению после этой ошибки.
3. ВЕРИФИКАЦИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ И
ПРОЦЕССОВ С ИСПОЛЬЗОВАНИЕМ ВРЕМЕННОЙ
ЛОГИКИ, ИНТЕРПРЕТИРУЕМОЙ НА ЯЗЫКЕ ПРОЛОГ
Ниже рассматривается процесс верификации и возможности
использования при этом языка Пролог. Язык Пролог имеет встроенный
мощный механизм логического вывода, что делает его привлекательным для
решения логических задач.
Под верификацией понимается проверка корректности и правильности
логического поведения системы. Считается, что система функционирует
корректно, если ее поведение отвечает ряду априори сформулированных
требований, причем существуют как общие, так и частные требования.
Общие требования относятся ко всем альтернативным вариантам систем
заданного класса. Частные требования относятся к конкретной системе и
отражают специфические детали ее функционирования. По отношению к
коммуникационным протоколам могут быть названы следующие общие
требования: отсутствие тупиков, полнота, отсутствие бесполезных
зацикливаний, недопустимость переполнения, соответствие терминальных
состояний поставленным в спецификациях целям.
При верификации системы могут использоваться как математические,
так и имитационные модели. В соответствии с модельным подходом
технологическая цепочка исследования системы будет следующей:
[Исследуемая система] → (Формализованное описание) → [Модель системы]
→(Исследование модели) → [Свойства модели] →(Интерпретация свойств
модели) → [Свойства системы] → (Проверка соответствия свойств системы
и предъявляемых к ней требованиям) → [Заключение о корректности
функционирования системы]. Здесь в квадратных скобках записаны
начальные, промежуточные и конечные результаты технологической
цепочки, а в круглых – совершаемые действия.
При использовании метода имитационного моделирования этап
«Исследование модели» может быть детализирован в виде следующей
цепочки: (Моделирование) → [Результаты моделирования] → (Анализ
результатов моделирования и вычленение свойств модели).
Для более целенаправленных действий при верификации с
использованием математических моделей может использоваться следующая
цепочка: [Исследуемая система] → (Формализованное описание системы и
предъявляемых к ней требований) → [Модель системы и выраженные в
терминах модели требования] → (Доказательство требуемых свойств
системы) → [Заключение о корректности функционирования системы]. В
данной главе будет рассматриваться именно эта цепочка, а также
интерпретация пропозициональной ветвящейся временной логики в
терминах логического программирования. Здесь же приводится
трансформация основных операторов пропозициональной ветвящейся
временной логики, называемой логикой дерева вычислений (Computation
Tree Logic, сокращенно CTL), в множество клозов языка Пролог [34].
Временная логика может быть основой метода верификации
вычислительных систем и процессов, если их можно представить в терминах
конечноавтоматной модели. Суть метода заключается в следующем. С
использованием спецификации системы составляются формулы временной
логики, представляющие определенные утверждения о ее
функционировании, которые необходимо доказать. Эти формулы
переводятся в прологовские клозы, которые интерпретируются на ЭВМ.
При интерпретации используется конечноавтоматная модель
функционирования системы, полученная каким-либо образом из ее
спецификации.
3.1. Логика дерева вычислений
Рассмотрим формальное определение логики дерева вычислений
(ЛДВ). Структура ЛДВ- модели есть тройка M=(S,R,P), где S – конечное
множество состояний; R
⊆ S
×
S – бинарное отношение на множестве S,
определяющее переходы между состояниями (s
i
,s
j
)
∈
R, если существует
переход из состояния s
i
в состояние s
j
; P – функция назначения состояниям
атомарных высказываний. Под атомарным высказыванием понимается
высказывание пропозициональной логики.
Определим множество ЛДВ-формул. Пусть Pa - множество атомарных
высказываний, а Р - множество ЛДВ-формул. Множество Р определяется
следующим образом:
1. Ра есть подмножество Р;
2. Если р1∈ Р, то ∼ р1 ∈ Р;
3. Если р1,р2 ∈ Р, то p1&p2 ∈ P, ALL(p1,p2)∈ P,
SOME(p1,p2) ∈ P, POT(p1,p2) ∈ P, INEV(p1,p2) ∈ P,
где ALL, SOME, POT, INEV - временные операторы.
Временные операторы POT и INEV введены для упрощения временных
логических выражений. Они могут быть получены из операторов ALL и
SOME с использованием следующих соотношений: POT(p1,p2), если
~ALL(p1,~p2);
INEV(p1,p2), если ~SOME(p1,~p2).
В дальнейшем для реализации вышеупомянутых четырех временных
операторов вводятся два вспомогательных оператора - PRE и PRETILDA.
Путь вычислений - это бесконечная последовательность состояний
(s
0,s1,s2,...), где ∀i (si,si+1) ∈ R. Запись M, s ╞ f или сокращенно s ╞ f означает,
что формула f выполнима в состоянии s структуры М. Отношение ╞
определяется следующим образом (в определении p1 и р2 - формулы ЛДВ):
1. s ╞ p, если атомарное высказывание р истинно в состоянии s;
2. s ╞ ~p, если ~(s ╞ p);
3. s ╞ p1&p2, если s ╞ p1 & s ╞ p2;
4.s
0
╞ ALL(p1,p2), если для каждого пути (s
0
,s
1
,...,s
k
) выполняется
следующее условие:
∀ i ((0 ≤ i ≤ k) & ∀ j ((0 ≤ j < i) → s
j
╞ p1)) → s
i
╞ p2.
Иными словами, ALL(p1,p2) истинно в узле s
0
дерева Т, если для каждого
пути Т, начинающегося из узла s
0
, p2 остается истинным, пока р1 не станет
ложным;
5. s
0
╞ SOME(p1,p2), если существует путь (s
0
,s
1
,...,s
k
) такой, что
∀ i ((0 ≤ i ≤ k) & ∀j ((0 ≤ j < i)→ s
j
╞ p1)) → s
i
╞ p.
Иными словами, SOME(p1,p2) истинно в узле s
0
дерева Т, если
существует путь в дереве Т, начинающийся из узла s
0
, и для данного пути р2
остается истинным, пока р1 не станет ложным;
6. s
0
╞ POT(p1,p2), если существует путь (s
0
,s
1
,...,s
k
) такой, что
∃ i ((0 ≤ i ≤ k) & ∀ j ((0 ≤ j < i) → s
j
╞ p1)) & s
i
╞ p2.
Иными словами, POT(p1,p2) истинно в узле s
0
дерева Т, если существует
путь, начинающийся из узла s
0
и оканчивающийся в узле s
i
, в котором р1
остается истинным до узла s
i
, и р2 истинно в узле s
i
;
7. s
0
╞ INEV(p1,p2), ecли для каждого пути (s
0
,s
1
,...,s
i
,...,s
k
) выполняется
следующее условие:
∃ i ((0 ≤ i ≤ k) & ∀ j ((0 ≤ j < i) → s
j
╞ p1)) & s
i
╞ p2.
Иными словами, INEV(p1,p2) истинно в узле s
0
дерева Т, если для
каждого пути, начинающегося из узла s
0
и оканчивающегося в узле s
i
, р1
остается истинным до узла s
i
, и р2 истинно в узле s
i
;
8. s ╞ PRE (p), если
∃
s' (s,s')
∈
R & s'╞ p.
Иными словами, PRE(p) в узле s дерева Т истинно, если существует
преемник узла s, где р истинно;
9. s ╞ PRETILDA (p), если
∀
s' (s,s')
∈
R → s'╞ p.
Иными словами, PRETILDA(p) в узле s дерева Т истинно, если для
каждого преемника узла s p истинно.
При вычислении формулы с вложенными временными операторами
необходимо определять состояния, на которых будут применяться более
"глубокие" операторы. Рассмотрим вычисление формулы
s ╞ OP1(OP2(p1,p2),OP3(p3,p4)).
Оператор OP1 будет оцениваться на состоянии s, в то время как
операторы OP2 и OP3 будут оцениваться на состояниях, определенных при
оценке OP1. Аналогично, р1 и р2, а также р3 и р4 будут оцениваться на
состояниях, определенных при вычислении OP2 и OP3 соответственно.
Формула р выполнима в структуре М, если существует такое состояние s
этой структуры, что М,s ╞ p. Формула р общезначима для структуры М, если
для каждого состояния s структуры М действительно М,s╞ p. Формула р
является теоремой, если она действительна для каждой модели М.
3.2. Интерпретация временной логики на языке Пролог
Оценка временных логических операторов основывается на их
рекурсивном вычислении с использованием языка Пролог. В данном учебном
пособии для этих целей используется версия Пролога - Arity Prolog,
используемая IBM-совместимых ПЭВМ [22].
3.2.1. Реализация POT - оператора
Реализация этого оператора задается следующим рекурсивным
уравнением:
T,s ╞ POT(p1,p2), если T,s ╞ p2 ∨ (p1 & PRE POT(p1,p2)) (3.3)
Каждая ЛДВ-формула определяет предикат Пролога. Формула s ╞ PRE
p представляется предикатом pre(p,l,s), где р - ЛДВ-формула, s - состояние
и l - список состояний. Роль списка состояний объясняется ниже. Отношение
R представляется предикатом arc, причем arc(s,t,s1) определяет, что переход
t изменяет состояние с s на s1. Для оценки формулы s ╞ p используется
предикат call.
Прологовская интерпретация формулы 3.1 определяется как
pre(P,L,S):-arc(S,T,S1),
P=..K,
insert(K,[L,S1],P0),
P01=..P0,
call(P01),!.
Оператор отсечения "!" обязывает интерпретатор Пролога искать
только первое решение, если оно существует.
Рассмотрим реализацию уравнения 3.3, касающегося оператора POT.
Представим данное уравнение в следующей форме:
T,s ╞ POT(p1,p2), если T,s ╞ p2 (3.4)
T,s ╞ POT(p1,p2), если T,s ╞ p1 & PRE POST(p1,p2) (3.5)
Прологовская реализация уравнения 3.4:
pot(P1,P2,L,S):-P2=..T,insert(T,[S],P0),P01=..P0,call(P01),!. (3.6)
Прологовская реализация уравнения 3.5:
pot(P1,P2,L,S):-P1=..T,insert(T,[S],P0),P01=..P0,call(P01),
pre(pot(P1,P2),[S|L],S). (3.7)
Хотя прологовские клозы 3.6 и 3.7 эквивалентны уравнениям 3.4 и 3.5, их
выполнение на практике не приносит ожидаемых результатов.
При их выполнении происходит зацикливание, поскольку невозможно
определить, было некоторое состояние пройдено или нет. Без ограничений
теоретической модели для избежания зацикливаний вводятся некоторые
ограничивающие условия при оценке временных операторов.
Эти условия используют список состояний l, введенный выше.
Список l строится в ходе оценки данного временного оператора и содержит
уже пройденные состояния. Данные условия реализуются с помощью
предиката outl. Предикат outl(s,l) истинен, если s не является элементом
списка l. Прологовское определение предиката outl следующее:
outl(S,[]):-!.
outl(S,[S1|L]):-noneg(S,S1),
outl(S,L).
где noneg(S,S1) - предикат, утверждающий, что S не равно S1.
noneg(S,S1):-remove(S,S1,[]),!,fail.
noneg(S,S1).
Если тот же самый предикат pot(p1,p2) оценивается в том же самом узле
s, то ответ должен быть отрицательным. Это условие предотвращает
бесконечное зацикливание. С учетом ограничивающего условия POT-
оператор определяется следующими прологовскими клозами:
pot(P1,P2,L,S):-outl(S,L),
P2=..T,insert(T,[S],P0),P01=..P0,call(P01),
!.
pot(P1,P2,L,S):-outl(S,L),
P1=..T,insert(T,[S],P0),P01=..P0,call(P01),
pre(pot(P1,P2),[S|L],S).
3.2.2. Реализация ALL-оператора
Реализация ALL-оператора задается следующим рекурсивным
уравнением:
T,s ╞ ALL(p1,p2), если T,s ╞ p2 & (~p1 ∨ PRETILDA ALL(p1,p2)) (3.8)
Формальное определение оператора PRETILDA задано формулой 3.2.
Прямая реализация этой формулы на языке Пролог невозможна из-за
наличия квантора всеобщности.Для трансформации формулы 3.2 в
эквивалентную, не содержащую квантор всеобщности, воспользуемся
известным соотношением:
∀x p(x) ↔ ∼ ∃ x ∼p(x)
В результате получается формула:
s ╞ PRETILDA p, если ∼∃s' ∼ ((s,s') ∈R → s'╞ p)
Заменяя операцию импликации в данной формуле, получаем формулу:
s ╞ PRETILDA p , если ~∃s'(s,s') ∈R & ∼(s'╞ p).
Эта формула может быть напрямую реализована путем расщепления ее на
две части:
S ╞ PRETILDA p ← ∼ CPRETILDA(p,s)
CPRETILDA(p,s) означает : ∃ s'(s,s') ∈ R & ∼ (s'╞ p)
Прологовская интерпретация этих двух выражений следующая:
pretilda(P,L,S):-non(cpretilda(P,L,S)).
cpretilda(P,L,S):-arc(S,T,S1),
P=..K,insert(K,[L,S1],P0),P01=..P0,
non(P01).
где non-предикат определяется как
non(P):-call(P),!,fail.
non(P).
Уравнение 3.8 трансформируется в клаузальную форму и
представляется в форме следующих прологовских клозов:
all(P1,P2,L,S):- P2=..T,insert(T,[S],P0),P02=..P0,call(P02),
P1=..K,insert(K,[S],P00),P01=..P00,non(P01),
!.
all(P1,P2,L,S):-P2=..T,insert(T,[S],P0),P02=..P0,call(P02),
pretilda(all(P1,P2),[S|L],S).
Однако оценка рекурсивного уравнения 3.8 с помощью данных
клозов невозможна ввиду отсутствия ограничивающих условий.
Если при попытке оценить предикат all(p1,p2) осуществляется
повторный переход в ранее рассмотренное состояние s, то данный
предикат необходимо оценить как истинный и прекратить дальнейшую
рекурсивную оценку для предотвращения зацикливания.
Для определения того, является ли объект элементом списка,
вводится предикат inl. Выражение inl(s,l) означает, что s является элементом
списка l. Прологовское определение предиката inl следующее:
inl(X,[Z|Y]):-remove(X,Z,[]),!.
inl(X,[Z|Y]):-inl(X,Y).
Используя предикат inl мы можем определить подходящее
ограничивающее условие и дать окончательное прологовское определение
ALL-оператора:
all(P1,P2,L,S):-inl(S,L),
!.
all(P1,P2,L,S):- P2=..T,insert(T,[S],P0),P02=..P0,call(P02),
P1=..K,insert(K,[S],P00),P01=..P00,non(P01),
!.
all(P1,P2,L,S):-P2=..T,insert(T,[S],P0),P02=..P0,call(P02),
pretilda(all(P1,P2),[S|L],S).
