Дубинин В.Н., Зинкин С.А. Языки логического программирования в проектировании вычислительных систем и сетей
Подождите немного. Документ загружается.

Переходы данной сетевой модели определяются с помощью следующих
клозов:
arc(S,seize(I),S1):-remove([idle(I),res],S,S2),
insert([cr(I)],S2,S1).
arc(S,release(I),S1):-remove([cr(I)],S,S2),
insert([idle(I),res],S2,S1).
Начальная маркировка сетевой модели определяется фактом:
init([idle(a),idle(b),res]).
Cледует отметить, что при описании сетевой модели выбраны Пролог-
ориентированные обозначения. При этом учитывается тот факт, что
переменные в Прологе записываются с большой буквы (например, буква I -
"И" большая латинская, не путать с единицей).
При использовании приведенных в разделе 1.4 клозов будут получены
следующие выходные данные, определяющие ГДС:
о достигнутых состояниях (база данных rstate):
0 [idle(a),idle(b),res] 1 [cr(a),idle(b)] 2 [cr(b),idle(a)]
о дугах ГДС (база данных gds):
0 seize(a) 1 1 release(a) 0 0 seize(b) 2 2 release(b) 0
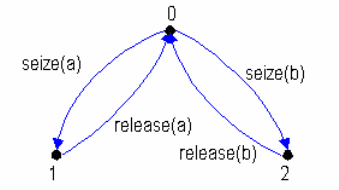
Графическое представление полученного ГДС приведено на рис.
2.4 . На основе визуального анализа данного ГДС можно сказать, что
соответствующая сетевая модель жива и безопасна, и, следовательно,
исходная система параллельных процессов свободна от тупиковых
ситуаций.
Рис.2.4.Граф достижимых состояний сетевой модели задачи взаимного
исключения
Анализ достигнутых маркировок показывает, что в системе отсутствует
ситуация, когда два процесса одновременно находятся в своих критических
областях.
2.3. Задача "обедающие философы"
Неформальное описание
Рассмотрим формулировку задачи об обедающих философах в
терминологии, предложенной Э. Дейкстрой [23,24]. За круглым столом
расставлены пять стульев, на каждом из которых сидит определенный
философ(Ф
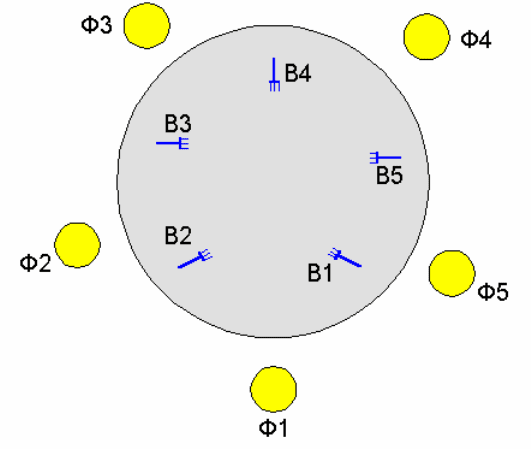
i) (рис. 2.5). В центре стола - большое блюдо спагетти, а на столе
лежат пять вилок (B1..B5) - каждая между двумя соседними тарелками.
Каждый философ может находиться только в двух состояниях - либо он
размышляет, либо ест спагетти. Начать думать философу ничто не мешает.
Но чтобы начать есть, философу нужны две вилки : одна в правой руке,
другая в левой. Закончив еду, философ кладет вилки слева и справа от своей
тарелки и опять начинает размышлять до тех пор, пока снова не
проголодается.
Рис.2.5.Задача об обедающих философах
Существует множество различных формулировок данной задачи, в одной
из которых философы интерпретируются как процессы, а вилки как ресурсы.
Задача "обедающие философы" удобна для изучения тупиковых ситуаций в
системах параллельных процессов.
В представленной задаче имеются две опасные ситуации : ситуация
голодной смерти и ситуации голодания отдельного философа. Ситуация
голодной смерти возникает в случае, когда философы одновременно
проголодаются и одновременно попытаются взять, например, свою левую
вилку. В данном случае возникает тупиковая ситуация, так как никто из них
не может начать есть, не имея второй вилки.
Одним из общих методов избежания тупиков является введение ограничений
на число параллельно выполняющихся процессов и ужесточение режима
использования ресурсов [25]. Например, тупиковую ситуацию голодной
смерти можно избежать, если наложить следующее условие использования
вилок - "философу разрешается взять две необходимые для еды вилки в том
случае, если они обе свободны". В качестве другого приема,
позволяющего избежать данную тупиковую ситуацию, является ограничение
числа одновременно сидящих за столом философов (например, до четырех).
Для этого, однако, необходимо скорректировать условие задачи и
предположить, что стол расположен в столовой, при входе в которую
находится швейцар, следящий за числом философов в столовой.
Ситуация голодания возникает в случае заговора двух соседей слева и
справа против философа, в отношении которого строятся козни.
Заговорщики поочередно забирают вилки то слева, то справа от него. Такие
согласованные действия злоумышленников приводят жертву к
вынужденному голоданию, так как он никогда не может воспользоваться
обеими вилками.
Сетевая модель
Предикатная сеть, представляющая задачу об обедающих философах,
изображена на рис. 2.6. Метка в сетевой модели, соответствующая
философу, имеет один атрибут - номер философа из множества {1,2,3,4,5}.
Каждому философу поставлен в соответствие свой номер. Метка,
соответствующая вилке, имеет один атрибут - номер вилки из множества
{1,2,3,4,5}. Каждой вилке поставлен в соответствие свой номер.
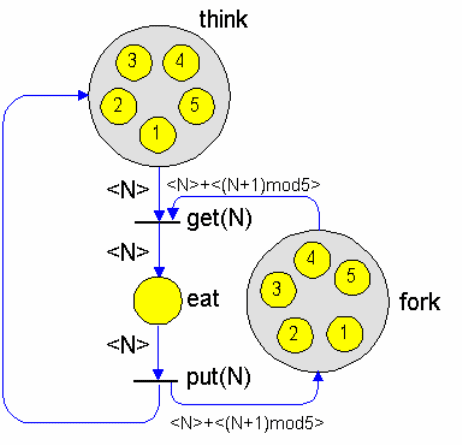
Рис.2.6.Сетевая модель задачи об обедающих философах
Интерпретация позиций сетевой модели следующая: позиция fork
определяет свободные в обращении вилки. Позиция think определяет
находящихся в размышлении философов. Позиция eat определяет
философов, находящихся в состоянии потребления пищи.
Ниже представлены переходы сетевой модели и дана их
интерпретация и выполняемые действия. Переход get(N) - "Переход N-го
философа из состояния размышления в состояние потребления пищи,
захват соседних вилок, то есть вилок с номерами N и (N+1)mod5". Переход
put(N) - "Переход N-го философа из состояния потребления пищи в
состояние размышления, возврат соседних вилок".
Переходы сетевой модели описываются следующими клозами:
аrc(S,get(N),S1):-
inlist(think(N),S),
mod5(N,NN),
remove([think(N),fork(N),fork(NN)],S,S2),
insert([eat(N)],S2,S1).
arc(S,put(N),S1):-
inlist(eat(N),S),
mod5(N,NN),
remove([eat(N)],S,S2),
insert([think(N),fork(N),fork(NN)],S2,S1).
Следует обратить внимание на представление переходов, несколько
отличное от описанного в разделе 1.3. В приведенных клозах перед
предикатом remove стоят еще два предиката. Это объясняется тем, что при
определении пре-условий необходимо знать закон, по которому связаны
номера N и NN, a именно NN=(N+1)mod5. Сложение по модулю 5
реализуется при помощи предиката mod5 cледующим образом:
mod5(X,XX):- X < 5,
XX is X + 1, !.
mod5(X,XX):- XX is 1.
Следует также заметить, что последнее предложение не эквивалентно
предложению с анонимной переменной,
mod5(_,XX):- XX is 1,
поскольку в последнем случае происходит расконкретизация переменной,
стоящей на первом месте в списке аргументов предиката mod5.
Предикат inlist(E,L) используется для определения принадлежности
элемента E списку L и определяется следующим образом:
inlist(X,[X|L]).
inlist(X,[Y|L]):-inlist(X,L).
Начальная маркировка сетевой модели определяется следующим
фактом:
init([think(1),think(2),think(3),think(4),think(5),
fork(1),fork(2),fork(3),fork(4),fork(5)]).
Следует отметить, что представленная сеть может моделировать
различные ситуации из различных проблемных областей.
Ниже представлены выходные данные, определяющие ГДС, полученные с
помощью клозов, определенных в разд. 1.4.
Достигнутые состояния (база данных rstate):
0 [think(1),think(2),think(3),think(4),think(5),fork(1),fork(2),
fork(3),fork(4),fork(5)]
1 [eat(1),think(2),think(3),think(4),think(5),fork(3),fork(4),fork(5)]
2 [eat(3),eat(1),think(2),think(4),think(5),fork(5)]
3 [think(1),fork(1),fork(2),eat(3),think(2),think(4),think(5),fork(5)]
4 [eat(5),think(1),fork(2),eat(3),think(2),think(4)]
5 [think(3),fork(3),fork(4),eat(5),think(1),fork(2),think(2),think(4)]
6 [eat(2),think(3),fork(4),eat(5),think(1),think(4)]
7 [think(5),fork(5),fork(1),eat(2),think(3),fork(4),think(1),think(4)]
8 [eat(4),think(5),fork(1),eat(2),think(3),think(1)]
9 [think(2),fork(2),fork(3),eat(4),think(5),fork(1),think(3),think(1)]
10 [eat(1),think(2),fork(3),eat(4),think(5),think(3)]
Дуги ГДС (база данных gds):
0 get(1) 1
1 get(3) 2
2 put(3) 1
5 get(3) 4
5 get(2) 6
6 put(2) 5
9 get(2) 8
9 get(1) 10
10 put(1) 9
1 get(4) 10
1 put(1) 0
0 get(2) 7
2 put(1) 3
3 get(1) 2
3 get(5) 4
4 put(5) 3
4 put(3) 5
6 put(5) 7
7 get(5) 6
7 get(4) 8
8 put(4) 7
8 put(2) 9
10 put(4) 1
9 put(4) 0
7 put(2) 0
5 put(5) 0
3 put(3) 0
0 get(3) 3
0 get(4) 9
0 get(5) 5
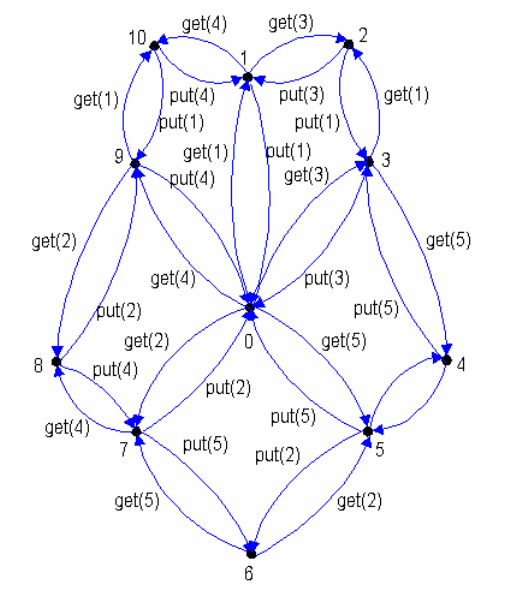
На рис. 2.7 полученный ГДС представлен в графическом виде. На основе
анализа данного ГДС можно сделать вывод, что соответствующая сетевая
модель является живой и, следовательно, исходная система параллельных
процессов свободна от тупиков.
Рис.2.7.Граф достижимых состояний сетевой модели задачи об обедающих
философах
Однако возможна ситуация голодания ("оттеснения") отдельного
философа, на что указывают определенные циклы в ГДС. Например,
следующий цикл:
M9
→
get(2)
→
M8
→
put(4)
→
M7
→
get(4)
→
(M8
→
get(2)
→
M9
соответствует оттеснению третьего философа от еды двумя его соседями -
вторым и четвертым философами. Они создают такую ситуацию, чтобы у
третьего философа не было одновременно двух необходимых для еды
вилок. В ГДС это соответствует тому, что из маркировок М7, М8, М9,
принадлежащих циклу, нет ни одной выходящей дуги, отмеченной
переходом get(3).
2.4. Алгоритм взаимного исключения в распределенной
вычислительной системе
Неформальное описание
Рассматриваемый алгоритм обеспечивает взаимное исключение
процессов в РВС, где узлы взаимодействуют только путем обмена
сообщениями и не имеют общей разделяемой памяти [34]. Этот алгоритм
позволяет проиллюстрировать способность предикатной сети иметь дело с
символическими последовательными номерами или временными пометками.
Узел РВС входит в критическую секцию только после того, как все
другие узлы были оповещены об этом намерении и ими были посланы
ответы, подтверждающие их согласие. Узел, делающий попытку войти в
критическую секцию, посылает запросное сообщение R всем другим
узлам. После приема сообщения R, другой узел или немедленно посылает
подтверждение А или откладывает ответ до тех пор, пока он не покинет
собственную критическую секцию. Предполагается, что узел,
принимающий запрос, может немедленно определить, кто первым войдет в
критическую секцию - он сам или запрашивающий узел. Узлу,
посылающему запрос, никогда не говорится о причинах выбора того или
иного решения, принятого опрашиваемым узлом. В ответ немедленно
посылается подтверждение А, если источник запроса имеет приоритет, в
других случаях подтверждение откладывается. Определение порядка
приоритетов осуществляется путем сравнения номеров временной
последовательности, присутствующих в каждом запросе. Если номера
данной последовательности равны, то для определения порядка вхождения
узлов в критические секции сравниваются их номера. Например,
приоритетнее может быть узел, порядковый номер которого больше.
Моделирование времени
Приводимая ниже модель алгоритма взаимного исключения интересна в
том смысле, что она является примером логико-временной спецификации
при помощи логического программирования. Использование в алгоритме
взаимного исключения временных пометок поставило следующие
проблемы: 1) Моделирование натуральных чисел, которые представляют
временные пометки; 2) Способность задавать эквивалентность между двумя
состояниями в различные моменты времени, но имеющих одну и ту же
семантику в рамках данной предикатной сети.
Модель, пригодная для символического выполнения, представляет
натуральные числа при помощи констант, которые могут быть получены при
помощи оператора следования. Ниже дается рекурсивное определение
натуральных чисел:
1) 0 - натуральное число;
2) Если х - натуральное число, то suc(x) - также натуральное число, где 0
является константой, а "suc" - оператор следования.
Модель натуральных чисел используется при моделировании времени.
Например, предположим, что в данный момент времени часы показывают 35
единиц времени. Обозначим данный момент времени как h. Следующим
значением времени на физических часах будет 36, что представляется как
suc(h) и т.д.
Интерпретация приведенного выше определения на языке Пролог проста.
Мы определяем константу "h" как момент времени в начальном состоянии, и
последующие моменты времени моделируются последовательностью suc(h),
suc(suc(h)),suc(suc(suc(h))), ...
Состояния сетевой модели сохраняют значения всех локальных времен.
Значения локальных времен имеют отношение к начальному состоянию (это
отношение определено для частных алгоритмов), но локальное время в
узле s
i модифицируется только переходом узла si.
Для того, чтобы определить эквивалентность двух состояний в различные
моменты времени, но имеющих одинаковую семантику в рамках сетевой
модели, рассматривается только отношение между локальными временами.
Минимальная модель выводится при поиске минимальной версии каждого
достижимого состояния. Состояние находится в своей минимальной версии,
если значение локальных часов данного состояния соответствует значению
локального времени в начальном состоянии.
Чтобы получить минимальную модель, значения часов всех узлов
пошагово уменьшаются до тех пор, пока не произойдет возврат к
начальному состоянию.
Запись shift(s,s
1) утверждает, что состояние s1 является минимальной
версией состояния s. Предикат shift определяется рекурсивно следующим
образом:
shift(S,S1):-shiftl(S,S2),
shift(S2,S1),
!.
shift(S,S).
Выражение shiftl(s,s2) утверждает, что состояние s2 непосредственно
меньшая версия состояния s, то есть мы уменьшаем значение часов в
состоянии s только на единицу времени. Предикат shiftl определяется
следующим образом:
shiftl([],[]):-!.
shiftl([E|S],[E1|S1]):-transfo(E,E1),
shiftl(S,S1).
Предикат transfo определяет временную трансформацию вида suc(h)
→
h для каждой позиции. Например, для позиции poz, предикат определяется
следующим фактом:
transfo(poz(suc(h)),poz(h)).
Применение предиката shift к каждому следующему состоянию
достигается путем модификации определения предиката arc:
arc(S,transition_name,S1):-
remove(preconditions,S,S2),
<data conditions>,
insert(postconditions,S2,S3),
shift(S3,S1).
Благодаря использованию предиката shift ГДС имеет ограниченное число
состояний. Состояния типа
I(site_a,suc(suc(...,suc(h)...))), I(site_b,suc(suc(...,suc(h)...)))
эквивалентны минимальным состояниям
I(site_a,h),I(site_b,h).
Сетевая модель
Переходы сетевой модели РВС, состоящей из двух узлов, имеют
следующую интерпретацию и конфигурацию:
1. Переход: send(I) -"Узел I посылает запрос и ждет подтверждения"
Пре-условия: idle(I,H)
Пост-условия: request(I,J,suc(H)),
waiting(I,suc(H),suc(H))
Условия по данным: others(I,J)
2. Переход: receive(I) - "Узел I посылает подтверждение и
входит в критическую секцию"
Пре-условия: ack(J,I),waiting(I,O,H)
Пост-условия: critical(I,H)
Условия по данным: Отсутствуют
3. Переход: release(I) -"Узел I покидает критическую секцию"
Пре-условия: critical(I,H)
Пост-условия: idle(I,H)
Условия по данным: Отсутствуют
4. Переход: i_reply(I) -"Свободный узел I посылает подтверждение"
Пре-условия: idle(I,H), request((J,I,O)
Пост-условия: ack(I,J), idle(I,K)
Условия по данным: others(I,J), max(H,O,K)
5. Переход: w_reply(I) -"Ожидающий узел I посылает подтверждение"
Пре-условия: waiting(I,OI,H), request(J,I,Oj)
Пост-условия: ack(I,J), waiting(I,OI,K)
Условия по данным: others(I,J), max((H,OJ,K),
priority(OJ,OI,J,I)
Условия по данным определяются с помощью предикатов others, max,
priority следующим образом:
others(site_a,site_b) - "Узел site_B является соседом узла site_A";
others(site_b,site_a) - "Узел site_A является соседом узла site_B".
max(X,X,X) - "Максимум из X и X есть X";
max(X,suc(X),suc(X)) - "Максимум из X и suc(X) есть suc(X)";
max(suc(X),X,suc(X)) - "Максимум из suc(X) и suc(X) есть suc(X)";
priority(X,suc(X),I,J) - "Узел I с локальным временем X имеет приоритет
над запрашивающим узлом J c временной пометкой suc(X) ";
priority(X,X,I,J):- order(I,J) - "Для определения приоритета двух узлов с
равными временными метками используется предопределенный порядок,
задаваемый предикатом order";
order(site_a,site_b) - "Приоритет узла site_a выше приоритета узла site_b".
Следует обратить внимание на индексацию переходов цветами из
множества {site_a,site_b}, что сделано для их выделения из множества
переходов с одинаковой семантикой относительно передающего и
принимающего узла.
Клозы, задающие переходы сетевой модели, имеют следующий вид:
arc(S,send(I),S1):-
remove([idle(I,H)],S,S2),
others(I,J),
insert([request(I,J,suc(H)),waiting(I,suc(H),suc(H))],S2,S3),
shift(S3,S1).
arc(S,receive(I),S1):-
remove([ack(J,I),waiting(I,O,H)],S,S2),
insert([critical(I,H)],S2,S3),
shift(S3,S1).
arc(S,release(I),S1):-
remove([critical(I,H)],S,S2),
insert([idle(I,H)],S2,S3),
shift(S3,S1).
