Дубинин В.Н., Зинкин С.А. Языки логического программирования в проектировании вычислительных систем и сетей
Подождите немного. Документ загружается.

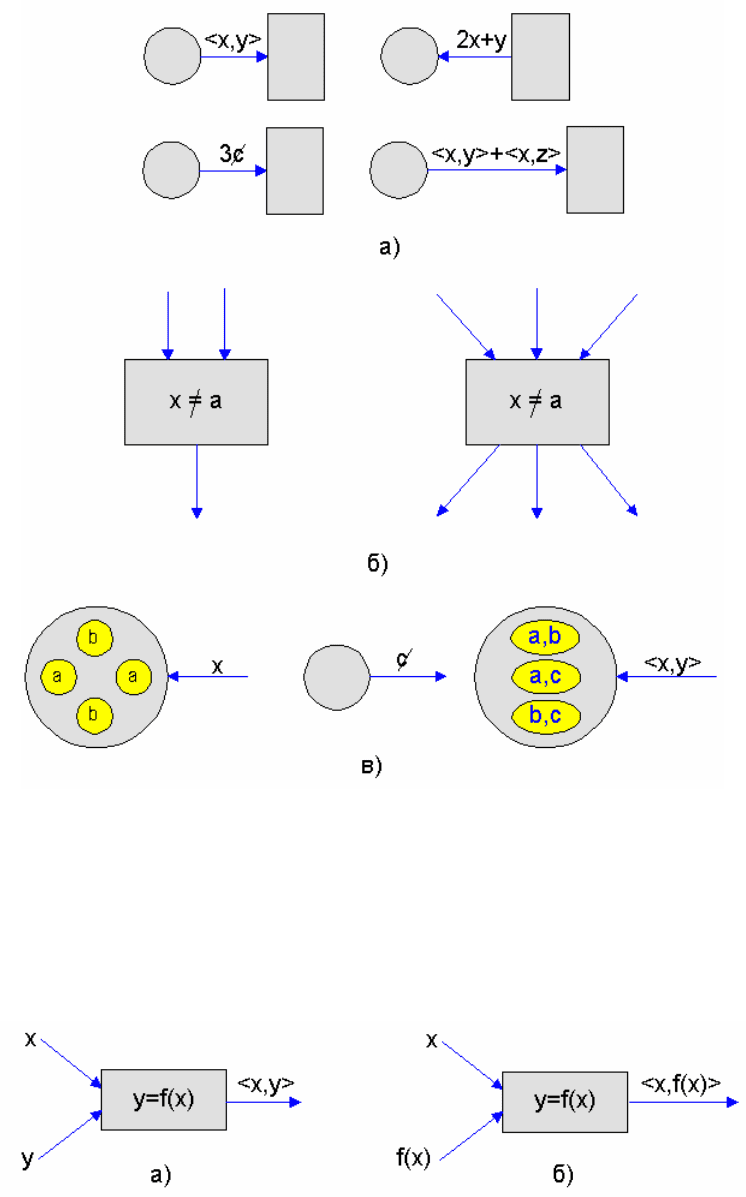
Ðèñ.1.1.Ýëåìåíòû ïðåäèêàòíîé ñåòè:
a-ïîìå÷åííûå äóãè
á-ïåðåõîäû ñ ëîãè÷åñêèìè ôîðìóëàìè;
â-ìàðêèðîâàííûå ïîçèöèè.
Рис.1.2.Замена переменных на дугах перехода на терм:
a-переход до замены;
б-переход после замены.
5) Маркировки М
0
позиций (предикатов) из Р формальными суммами
кортежей, составленных из индивидуальностей структуры ∑. Данные
кортежи будем называть метками. Примеры маркированных позиций
представлены на рис. 1.1,в .
6) Функции К, назначающей позициям верхнюю границу числа меток,
которые могут в них находиться. Число K(p) называется емкостью позиции р.
Позиции могут иметь бесконечную емкость. В дальнейшем, если не будет
оговорено особо, будем считать, что емкость позиций не ограничена.
7) Правил перехода, регламентирующих функционирование сетевой
модели.
Введем следующие определения. Для перехода t
i
∈ T определим следующие
множества:
I(t
i
) = {p
j
| p
j
∈ P и (p
j
, t
i
) ∈ F} – множество входных позиций
перехода t
j
(пре-условия перехода t
i
);
O(t
i
) = {p
j
| p
j
∈ P и (t
i
, p
j
) ∈ F} – множество выходных позиций
перехода t
i
(пост-условия перехода t
i
).
Входными дугами перехода t
i
будем называть дуги, ведущие к этому
переходу из позиций, принадлежащих множеству I(t
i
), а выходными – дуги,
ведущие из перехода t
i
к позициям из O(t
i
).
Подстановка σ есть отображение множества переменных V в
множество индивидуальностей А, σ:V → A. Подстановка может быть задана
множеством пар вида (x, σ(x)), где х ∈ V. Пусть X – кортеж и σ-подстановка.
Кортеж σ[X] получается одновременной заменой всех вхождений
переменных х в кортеже X на их образы σ(x). Кортеж Y называется
конкретизацией кортежа X, если существует подстановка σ такая, что Y = σ
[X]. При этом кортежи Y и X также будем называть сопоставимыми. Две
подстановки σ
1
: V
1
→ A и σ
2
: V
2
→ A назовем не противоречащими друг
другу, если ∀ v ∈ V
1 ∧
V
2
[σ
1
(v) = σ
2
(v)], т. е. если одним и тем же
переменным обе подстановки ставят в соответствие одни и те же
индивидуальности.
В предикатной сети определены следующие условия разрешенности и
правила срабатывания переходов. Переход t
i
∈
Т разрешен, если:
a) все позиции из множества I(t
i
) имеют метки. Если пометка дуги (p
k
,
t
i
) представляет формальную сумму из m кортежей, то в позиции p
k
должно
находиться по меньшей мере m меток. Для каждого кортежа, приписанного
входной дуге (p
k
, t
i
), должна существовать такая подстановка σ
j
, что в
позиции p
k
будет метка, являющаяся конкретизацией данного кортежа.
Иными словами, в позиции p
k
должна существовать сопоставимая с
кортежом метка. Назовем подстановку σ
j
сопоставляющей. Сопоставление
различным кортежам одной и той же метки не допускается;
б) существуют не противоречащие друг другу сопоставляющие
подстановки для всех кортежей, приписанных входным дугам перехода t
i
.
Объединение таких подстановок назовем общей сопоставляющей
подстановкой;
в) существует общая сопоставляющая подстановка, при которой
логическая формула, приписанная переходу, становится истинной. Такую
подстановку назовем разрешающей подстановкой;
г) при добавлении соответствующего числа меток в выходные позиции
не будет превышена емкость ни одной из них. Число добавляемых меток в
выходную позицию определяется по числу кортежей в формальной сумме,
помечающей выходную дугу.
Сработать может только разрешенный переход. При срабатывании
перехода t
i
метки из его входных позиций удаляются, а в выходные –
добавляются. Число меток, удаляемых из позиции p
k
∈ I(t
i
)), определяется
числом кортежей, входящих в формальную сумму, приписанную дуге (p
k
, t
i
).
Причем из позиции p
k
будут удалены только те метки, которые были
сопоставлены кортежам из этой формальной суммы. Число меток,
добавляемых в позицию p
l
∈ O(t
i
), определяется числом кортежей,
входящих в формальную сумму, приписанную выходной дуге (t
i
, p
l
).
Добавляемые метки получаются путем конкретизации соответствующих
кортежей с помощью разрешающей подстановки.
Сетевая модель функционирует, переходя от одной маркировки к
другой, начиная от начальной. Переход от маркировки М к маркировке
′
M
в
результате срабатывания перехода t обозначается как
MM
t
→
′
. Eсли
существуют переходы t
1
, t
2
,..., t
n
, такие, что MM
i
t
i
i
→
+1
(i = 1,2,...,n) для
маркировок M
1
, M
2
,..., M
n+1
, то говорят, что M
n+1
достижима из M
1
при
последовательности срабатывания переходов σ = t
1
t
2
...t
n
.
Проиллюстрируем функционирование предикатной сети на примерах.
Рассмотрим сетевую модель, изображенную на рис. 1.3. Данная сетевая
модель описывает часть семейных отношений, а именно, определяет
отношение «Быть прародителем» (под «прародителем» понимается родитель
родителя): «Субъект x является «прародителем» субъекта y, если x является
родителем z, a z является родителем y». Если позиция «Родитель»
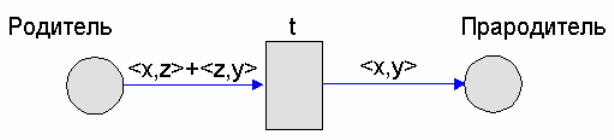
маркирована двумя метками <Юрий, Михаил> и <Евгений, Сергей>, то
переход t неразрешен, так как не существует непротиворечащих
сопоставляющих подстановок для кортежей <x, z> и <z, y>. Если же позиция
«Родитель» маркирована двумя метками <Юрий, Михаил> и
<Михаил, Сергей>, то переход t является разрешенным. Разрешающая
подстановка имеет следующий вид: {(x, Юрий), (y, Сергей), (z, Михаил)}.
При срабатывании перехода t обе метки удаляются из позиции «Родитель», а
в позицию «Прародитель» добавляется метка <Юрий, Сергей>. Появление
данной метки в позиции «Прародитель» можно проинтерпретировать так:
«Юрий является прародителем Сергея».
Ðèñ.1.3.Ñåòåâàÿ ìîäåëü, îïèñûâàþùàÿ ÷àñòü ñåìåéíûõ îòíîøåíèé
Предикатная сеть, изображенная на рис. 1.4, используется для
доказательства того, что Сократ смертен. Пусть позиция Р1 данной сетевой
модели начально маркирована меткой <Сократ, грек>. При данной
маркировке переход t
2
неразрешен, а переход t
1
– разрешен. При
срабатывании перехода t
1
метка <Сократ, грек> удаляется из позиции Р1,
одновременно с этим в позицию Р1 добавляется метка <Сократ, человек>.
Становится разрешенным переход t2. При срабатывании перехода t2 метка
<Сократ, человек> удаляется из позиции Р1, одновременно с этим в позицию
Р1 добавляется метка <Сократ, смертен>. Рассмотрим сетевую модель,
представленную на рис. 1.5,а. Пусть задана структура ∑ = ({a,b,c}; :=), где :=
есть отношение упорядочения по алфавиту, и функция K: P → {3}. При
данных условиях в представленной сетевой модели имеются две
разрешающие подстановки. Из-за наличия конфликта может быть выбрана
только одна из них. При выборе подстановки {(x,a), (y,b), (z,c)}
результирующую маркировку, полученную в результате срабатывания
перехода t
1
, можно увидеть на рис. 1.5,б.
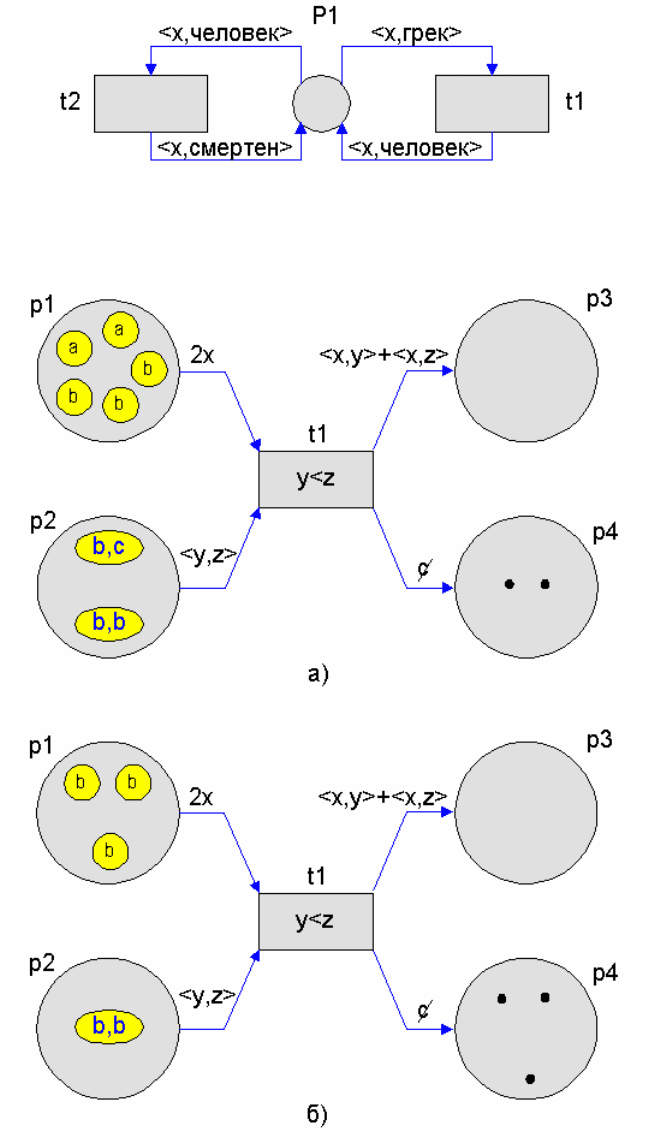
Ðèñ.1.4.Ñåòåâàÿ ìîäåëü äëÿ äîêàçàòåëüñòâà ñìåðòíîñòè Ñîêðàòà
Ðèñ.1.5.Ïðèìåð ôóíêöèîíèðîâàíèÿ ñåòåâîé ìîäåëè:
a-ñåòåâàÿ ìîäåëü äî ñðàáàòûâàíèÿ ïåðåõîäà;
á-ñåòåâàÿ ìîäåëü ïîñëå ñðàáàòûâàíèÿ.
Следует отметить, что интерпретация предикатных сетей на языке
Пролог способствует их модификации: внесению свойства
саморазвертываемости и самомодифицируемости, структуризации набора
цветов метки. При этом метка представляется в виде дерева, листьями
которого являются цвета метки, а промежуточными вершинами – имена
определенных подструктур. Корневая вершина дерева является именем
метки. Соответствующим образом данное расширение касается пометки дуг
и правил работы перехода. При желании можно перейти от иерархически
структурированной метки к одноуровневому ее представлению. При этом
имена подструктур преобразуются в цвета метки. Иерархически
структурированную метку удобно представлять с помощью термов языка
Пролог.
1.2. Некоторые свойства сетевых моделей
Кратко рассмотрим некоторые свойства сетевых моделей.
Обозначим через L(N,M) множество всех последовательностей
срабатывания для сети N, начинающихся из маркировки М, через #(t,
σ
) -
количество появлений символа t в последовательности
σ
, а через R(N,M) -
множество всех маркировок, достижимых из М. В качестве синонима
термина «маркировка» в дальнейшем будем использовать также термин
«состояние». Обозначим N ={1,2,...}.
Позиция р сети N называется к-ограниченной, если ∀М’∈ R(N,M),
M’(p) ≤ k. Сеть называется к-ограниченной, если все ее позиции к-
ограничены. 1-ограниченную позицию (сеть) называют безопасной.
Переход t ∈ T живой при маркировке M
o в сети N, если ∀
σ
∈
L(N,M
o), ∃
σ
’ ∈ T [
σσ
’t ∈ L(N,Mo )] или
∀M’∈ R(N,M
o ), ∃M
″
∈ R(N,M’)[enable(t,M
″
)], где
enable(t,M
″
) означает, что переход t разрешен при маркировке M
″
.
Переход t ∈ T условно-живой при маркировке М
o в сети N, если
∀n ∈ N , ∃
σ
∈ L(N,Mo ) [#(t,
σ
) ≥ n].
Переход t ∈ T потенциально-живой при маркировке М
o в сети N, если
∃M’ ∈ R(N,M
o)∀ M’’ ∈ R(N,M’) M’’’ ∈ R(N,M
″
)[enable(t,M’’’)].
Переход t ∈ T частично-мертвый при маркировке M
o в сети N, если ∃n
∈ N , ∀
σ
∈ L(N,Mo ) [#(t,
σ
)<=n].
Переход t ∈ T мертвый при маркировке M
o в сети N, если
∀
σ
L(N,Mo ) [#(t,
σ
)=0].
Сеть N - живая (условно-живая, частично-мертвая, мертвая) при маркировке
M, если каждый ее переход живой (условно-живой, частично-мертвый,
мертвый) при маркировке M.
Маркировка M’ ∈ R(N,M ) называется тупиковой, если
∃ t ∈ T [enable(t,M )].
Можно выделить следующие основные методы исследования
предикатных сетей, используемые при верификации: методы линейной
алгебры (матричный анализ) [23], построение множества (или графа)
достижимых состояний, имитационное моделирование [29,30]. С
использованием методов линейной алгебры обычно определяются P-ин-
варианты и Т-инварианты. Р-инвариант - это линейное отношение на
маркировке подмножества позиций, выражающееся в том, что взвешенная
сумма различных меток в позициях является константой и равна значению,
определяемому начальной маркировкой. Если в Р-инвариант входят все
позиции сетевой модели, то такая сетевая модель является ограниченной.
Т-инвариант соответствует последовательности срабатываний переходов,
переводящей сеть из маркировки М в ту же самую маркировку М. Если Т-
инвариант включает все переходы сети, то она жива.
При верификации на основе предикатных сетей может использоваться
также так называемый метод «структурной индукции». Пусть необходимо
проверить свойство Р, например, инвариант. Это свойство проверяется при
начальной маркировке, затем допускается, что это свойство верно при
произвольной маркировке М, после чего доказывается сохранение этого
свойства после срабатывания произвольного перехода.
Граф достижимых состояний (ГДС) сетевой модели N есть
ориентированный граф G
N = (V,E,L), где V - множество вершин, равное
множеству достижимых состояний сетевой модели; E ⊆V x V - множество
дуг такое, что (s
i,sj) ∈ E, если состояние sj непосредственно достижимо из
состояния s
i; L:E
→
T - функция разметки дуг именами переходов такая, что
L(si,sj)=t, если состояние sj непосредственно достижимо из состояния si при
срабатывании перехода t. Анализ свойств сетевой модели по ГДС дает
наиболее полную характеристику ее поведения, поскольку ГДС
перечисляет все состояния и все последовательности срабатываний.
Свойство живости распознается, например, по наличию
последовательностей срабатывания, начинающихся в каждом достижимом
(из начального) состоянии и ведущих в начальное состояние. Следует
отметить, что некоторые свойства сетевой модели могут быть легко
получены на основе визуального анализа ГДС, при этом само графическое
представление должно быть небольшим и обозримым для восприятия.

1.3. Представление предикатных сетей на языке Пролог
Для представления предикатных сетей используется язык логического
программирования Пролог. В общем случае Пролог-программа
представляется совокупностью хорновских клозов вида:
B :- A
1
, ..., A
n
,
где A
i
(i=
1, n
) является условием, а В – заключением. Выполнение всех
условий А
1
, ..., А
n
влечет заключение В. Все А
i
и В являются атомарными
формулами, имеющими вид Р(t
1
,...,t
k
), где Р – k-арный предикатный символ,
а t
i
(i=
1, k ) – терм. Терм может быть переменной, функцией или константой.
Хорновский дизъюнкт имеет нуль или более условий и не более одного
заключения. Существует четыре различные формы хорновских клозов в
свете их процедурной интерпретации:
1) В клозе присутствуют и условия, и заключение:
B :- A
1
, ..., A
n
(n
≥
1).
Этот сорт хорновских клозов интерпретируется как декларация
процедуры. Заключение B интерпретируется как имя процедуры, множество
условий {A
1
, ..., A
n
} интерпретируется как тело процедуры;
2) В клозе присутствует только заключение:
B :–
Этот сорт хорновских клозов интерпретируется как утверждение факта;
3) В клозе присутствуют только условия:
:– A
1
, ..., A
n
(n
≥
1)
Этот сорт хорновских клозов интерпретируется как целевое
утверждение, представленное в форме отрицания.
Ниже рассматриваются правила кодировки предикатных сетей на языке
Пролог. Полученный набор клозов может использоваться для интерпретации
сетевой модели. В дальнейшем рассматриваются сетевые модели с
позициями, имеющими бесконечную емкость. Предполагаем, что имена
элементов сетевой модели совпадают с именами их представлений в Пролог-
программе.

Маркировка предикатной сети представляется списком, состоящим из термов
следующего вида:
pname(a
1
, a
2
, ..., a
n
),
где pname – имя маркированной позиции (символьная константа),
(a
1
, a
2
, ..., a
n
) – кортеж индивидуальностей, представляющий метку,
находящуюся в позиции pname, где а
i
– символьная константа языка Пролог.
При использовании расширенных предикатных сетей символ а
i
может быть
термом языка Пролог, включающим только символьные константы или
константные термы. Функторы внутренних термов, входящих в рассматрива-
емый внешний терм, представляющий метку, определяют соответствующие
имена подструктур данной метки. Если в позиции pname находится m меток,
то число термов с функтором pname в списке должно быть также равно m.
Каждый переход сетевой модели представляется клозом следующего
вида:
arc(S,transition_name,S1):-
remove(preconditions,S,S2),
<data conditions>,
insert(postconditions,S2,S1).
Предикат arc(S,transition_name,S1) является истинным, если при
срабатывании перехода transition_name сетевая модель переходит из
маркировки S к маркировке S1.
Переход transition_name представляется либо символьной константой
tname, либо термом вида:
tname(X
1
, ..., X
f
),
где tname – имя перехода: X
i
(i=
1, f ) – переменные, встречающиеся в пометке
входных дуг данного перехода. Определение перехода с помощью терма
используется для возможности его индексирования.
С использованием списка preconditions определяется истинность
условий разрешенности перехода, отмеченных выше буквами a и б. Список
preconditions состоит из термов следующего вида:
pname(X
1
, X
2
, ..., X
k
),
где pname – имя входной позиции перехода transition_name; (X
1
, X
2
, ...,
X
k
) – кортеж из переменных и индивидуальностей, входящий в пометку
входной дуги (pname, transition_name) предикатной сети. В расширенных
предикатных сетях элемент X
i
может быть термом. Следует отметить, что
терм с функтором pname встречается в списке preconditions столько раз,
сколько кортежей в формальной сумме, помечающей дугу
(pname, transition_name). Если данная дуга отмечена символом ⊄, то
соответствующий терм вырождается в символьную константу pname. В
списке preconditions должны фигурировать имена всех входных позиций
перехода.
Язык Пролог имеет мощный встроенный механизм подстановки и
конкретизации, что позволяет компактно и элегантно выразить условия
разрешенности перехода, отмеченные буквами a и б. Для проверки данных
условий разрешенности используется предикат remove.
Предикат remove(preconditions,S,S2) является истинным, если имеется
такая конкретизация термов в списке preconditions, что при их удалении из
маркировки S получается маркировка S2.
Предикат remove определяется с помощью следующих клозов:
remove([E|X], L2, L3) :– delel(E, L2, LP), remove(X, LP, L3).
remove([ ], L, L).
Предикат delel используется для удаления элемента из списка.
Предикат delel(E, L2, LP) истинен, если элемент Е содержится в списке L2
и при удалении этого элемента из списка L2 получается список LP. Предикат
delel определяется следующим образом:
delel(X, [X | L], L).
delel(X, [Y | L], [Y | L1]) :- delel(X, L, L1).
Условия по данным <data conditions> представляют логическую
формулу (см. п. 4 определения предикатных сетей), приписанную переходу
и выраженную средствами языка Пролог. С помощью данных условий
определяется истинность условия разрешенности перехода, отмеченная
буквой с. У перехода могут отсутствовать условия по данным. Условия по
данным могут использоваться не только для определения условий
разрешенности перехода, но и для манипулирования данными, что согла-
суется с определением предикатных сетей (см. рис. 1.2 ).
С использованием списка postconditions определяются метки,
добавляемые в выходные позиции перехода при его срабатывании. Список
postconditions состоит из термов следующего вида:
pname(X
1
, X
2
, ..., X
q
),
где pname – имя выходной позиции перехода transition_name; (X
1
, X
2
, ...,
X
q
) – кортеж из переменных и индивидуальностей, входящий в пометку
выходной дуги (transition_name, pname) предикатной сети. В расширенных
предикатных сетях элемент X
i
может быть термом. Следует отметить, что
терм с функтором pname встречается в списке postconditions столько раз,
сколько кортежей в формальной сумме, помечающей дугу (transition_name,
pname). Если данная дуга отмечена символом ⊄, то соответствующий терм
