Drennan R.D. Statistics for Archaeologists: A Common Sense Approach

Подождите немного. Документ загружается.

SIMILARITIES BETWEEN CASES 283

Statpacks and Reporting Results

Measuring similarities between cases runs against the grain of the usual orga-

nization of statpacks, which are designed to work with variables rather than

cases. Some statpacks nonetheless provide options for calculating similarity

indexes between cases. Different statpacks vary quite substantially in how this

is accomplished. In some, there is a speciﬁc set of options for measuring simi-

larities between cases. In others, it is necessary to transpose the entire dataset

so that rows (cases) become columns (variables) and columns become rows.

Then the usual structure of measuring relationships between variables becomes

a question of relationships between cases instead. In yet other statpacks, mea-

suring similarities between cases is not a separate task but instead is embedded

in the routines that perform a multivariate analysis that begins with similarities

between cases. The statpack that will calculate the full variety of coefﬁcients of

similarity between cases discussed in this chapter is rare. There are, however,

stand-alone specialty programs that perform just this task.

Whatever the software solution, in reporting the results of any multivariate

analysis that starts with the measurement of similarities between cases, it is

essential to specify how the similarities were measured. The choice of similar-

ity coefﬁcient has a major bearing on the outcome of a multivariate analysis,

and the reader should always be made explicitly aware of that choice and the

reasons for it.

consistent with this result, since Household Units 14 and 20 have quite different

values for most of the variables. These calculations of Gower’s Coefﬁcient then jibe

with the original data, reassuring us both that the choice of coefﬁcient makes sense,

and that it was calculated correctly.

Chapter 23

Multidimensional Scaling

Conﬁgurations in Different Numbers of Dimensions............................................. 286

Interpreting the Conﬁguration ..................................................................... 289

Multidimensional scaling is perhaps in concept the simplest and most intuitive of

the various approaches to multivariate analysis, and this can rightly be regarded as

a major advantage. It is difﬁcult to misunderstand the principles upon which it is

based. A multidimensional scaling takes as its starting point a matrix of similarity

(or dissimilarity) scores between cases like the one in Table

22.9. The analysis con-

sists of an iterative, trial-and-error process of creating a conﬁguration of points, each

representing one of the cases in the dataset. These points representing the cases are

placed in space in such a way that the rank order of the distances between the pairs

of points corresponds as well as possible to the rank order of the similarity coefﬁ-

cients in space. That is to say, the aim of the conﬁguration is to place the two points

representing the two most similar cases closer to each other than any other pair of

points in the conﬁguration. The two points representing the second highest simi-

larity score should be the second-closest pair of points, and so on. Finally, the two

cases with the lowest similarity score should be the two points farthest apart in the

conﬁguration. In this very simple way, multidimensional scaling attempts to draw a

picture of the relationships between cases that are encapsulated in the matrix of sim-

ilarity coefﬁcients. Since only a rank order correlation is sought between similarity

scores and distances between pairs of points, multidimensional scaling is sometimes

referred to as nonmetric multidimensional scaling.

The conceptual simplicity of multidimensional scaling masks the ﬁercely com-

plex challenge of writing a program to produce such a conﬁguration of points.

A multidimensional scaling program must set up an initial conﬁguration by plac-

ing points representing all the cases in space, and then tinker with that conﬁg-

uration, moving some points to new locations to see whether that improves the

rank order correlation between distances between pairs of points and similarity

R.D. Drennan, Statistics for Archaeologists, Interdisciplinary Contributions

to Archaeology, DOI 10.1007/978-1-4419-0413-3

23,

 Springer Science+Business Media, LLC 2004, 2009

285

286 CHAPTER 23

coefﬁcients between pairs of cases. This is done over and over until no improve-

ment can be found. As multidimensional scaling was developed, it was not unusual

to get different results from different programs, but the algorithms for this iterative

procedure are now honed enough that all the programs currently in use are pretty

much equivalent. Some, but not all, large statpacks will perform multidimensional

scaling.

It is easy to visualize multidimensional scaling in two dimensions, and even

in three, but multidimensional scaling solutions can have more dimensions than

physical space does. A perfect rank order correlation between similarity scores and

distances between pairs of points can always be achieved in one less dimension than

the number of variables. For the Ixcaquixtla household unit dataset, for example,

which has ten variables, a conﬁguration of points representing a perfect rank order

correlation between similarity scores and distances between pairs of points can be

achieved in nine dimensions. Since multidimensional scaling results are interpreted

by looking at the conﬁguration, however, this is an unsatisfactory solution. Looking

at a conﬁguration of points in nine dimensions is unbearably cumbersome – more

difﬁcult than simply looking at the original data table to hunt for patterns. The game,

then, is to produce as good a rank order correspondence between similarity scores

and distances between point pairs as possible in as few dimensions as possible. The

smaller the number of dimensions, the easier it is to look at and interpret a multidi-

mensional scaling conﬁguration, so it is a great advantage to produce a conﬁguration

that represents the patterns in the similarity scores, not perfectly, but very accurately

in very few dimensions. For any dataset, the larger the number of dimensions, the

stronger the rank order correlation will be between distances between pairs of points

and similarity scores between pairs of cases.

CONFIGURATIONS IN DIFFERENT NUMBERS

OF DIMENSIONS

Carrying out multidimensional scaling starts by asking a statpack to take a set

of similarity scores between cases (as described in Chapter 22) and produce the

best possible conﬁguration in one dimension. A one-dimensional conﬁguration, of

course, is an arrangement of points representing the cases along a line. Multidimen-

sional scaling can be based on any one of several different rank order correlations,

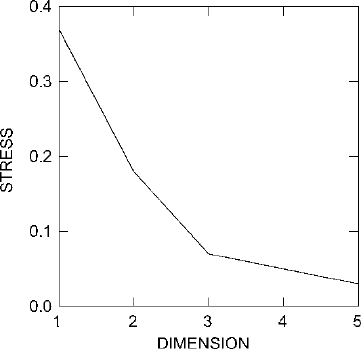
which are commonly referred to in this context as stress values. The different stress

coefﬁcients generally do not produce very different results. The lower the stress

value, the better the rank order correlation between similarity scores and distances

between pairs of points. For the matrix of similarity scores between Ixcaquixtla

household units from Table

22.9, a one-dimensional conﬁguration can be produced

that has a ﬁnal stress value of 0.3706. It is called a “ﬁnal” stress value because

the procedure is iterative, and a stress value is calculated at each step in the pro-

cess. The iteration history of this scaling began with an initial conﬁguration with

a stress value of 0.4452. After the ﬁrst successful iteration, which improved the

MULTIDIMENSIONAL SCALING 287

conﬁguration, the stress value was 0.4139. It then continued to drop, iteration by

iteration, to 0.3988, 0.3874, 0.3795, 0.3709, 0.3707, and ﬁnally 0.3706. Beyond

this, the algorithm could make no further improvement, and the analysis concluded.

A stress value of 0.3706 is fairly high, and there was little intelligible patterning to

be observed in the one-dimensional linear conﬁguration.

The process is then repeated for two dimensions, which arranges points on a ﬂat

plane, easily represented as a scatter plot. For the Ixcaquixtla household dataset,

the ﬁnal stress value for the two-dimensional conﬁguration is 0.1813, a substan-

tial improvement over the 0.3706 of the one-dimensional conﬁguration. We know

that a three-dimensional conﬁguration will enable an even better rank order cor-

relation between similarity scores and distances between pairs of points. For the

Ixcaquixtla data, the three-dimensional conﬁguration yields a ﬁnal stress value of

0.0726, another substantial improvement. There is further improvement in four

dimensions, with the stress declining to 0.0465; and in ﬁve dimensions, with the

stress down to 0.0332.

In practice, one must decide which conﬁguration (the one-dimensional one,

the two-dimensional one, the three-dimensional one, etc.) to attempt to interpret.

Since interpretation centers on the examination of plots of the conﬁguration of

points, it is unusual to attempt to interpret a scaling in more than three dimen-

sions. It simply becomes too cumbersome to attempt to visualize and inspect a

conﬁguration of points in more dimensions than actual physical space provides.

A two-dimensional conﬁguration is easier to inspect than a three-dimensional one,

and a one-dimensional conﬁguration is easier still to inspect. A one-dimensional

conﬁguration will not, however, be at all easy to interpret if it does not provide a rea-

sonably accurate picture of the pattern of relationships between cases encapsulated

Figure 23.1. Graph of declining ﬁnal stress values for analysis of Ixcaquixtla household data with

increasing number of dimensions.

288 CHAPTER 23

in the matrix of similarity scores. It is the stress value that indicates how accurate a

picture it is.

Sometimes it is helpful to look at a plot of declining stress values like the one in

Fig.

23.1. This shows the high stress value for one dimension mentioned above, the

much lower stress value for two dimensions, and an additional substantial decline

in stress for the three-dimensional conﬁguration. Beyond this, in four and ﬁve

dimensions, the stress continues to decline, as it always will, but at a much slower

pace. This “elbow” in the graph of declining stress value is an indication that the

three-dimensional conﬁguration may be a good representation of the patterns in the

dataset, and that, since there is less improvement in four and ﬁve dimensions, there

may be little to be gained in looking at these conﬁgurations. There is also a useful

rule of thumb that stress values of about 0.1500 or less are often associated with

interpretable conﬁgurations. For the Ixcaquixtla household scaling, it is the three-

dimensional conﬁguration that breaks through to a stress value below 0.1500. For

this reason, then, and because of the elbow in the graph at three dimensions, it seems

likely that the three-dimensional conﬁguration will be an effective representation of

the patterning in the dataset.

Table 23.1. Coordinates in Three Dimensions of the

Multidimensional Scaling of Household Units from Ixcaquixtla

Household Unit Dimension 1 Dimension 2 Dimension 3

1 −0.285 0.301 0.142

2 −1.069 −0.003 − 0. 083

30.996 −0.568 0.523

40.062 0.421 −0.088

5 −0.963 0.011 0.224

60.970 0.056 −0.517

70.178 0.619 0.427

8 −0.146 0.425 −0. 624

9 −1.228 −0.008 − 0. 159

10 −0.059 0.348 −0.105

11 0.739 −0.761 −0.830

12 0.314 0.626 0.216

13 0.102 −0.466 −1.261

14 −0.541 −1.384 0.527

15 −0.881 0.064 0.024

16 0.817 0.017 0.716

17 0.504 0.780 − 0. 242

18 0.382 −0.935 0.504

19 −0.121 −0.305 0.082

20 0.229 0.762 0.524

MULTIDIMENSIONAL SCALING 289

INTERPRETING THE CONFIGURATION

The essential element in the results of this analysis, as always with multidimen-

sional scaling, is the list of coordinates for each case in the three dimensions

(Table

23.1). Inspecting a multidimensional scaling conﬁguration usually means

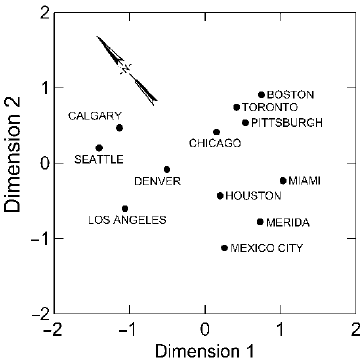
plotting the points on a graph to examine their relationships. For some datasets,

simply plotting the points and labeling them makes the patterning clear, as seen in

Fig.

23.2. This two-dimensional scaling conﬁguration was produced from a matrix

of Euclidean distances in real space – the matrix of distances between each pair of

cities. With only this information, a multidimensional scaling analysis placed the

cities in a two-dimensional conﬁguration that represents their actual physical loca-

tions quite accurately. Simply labeling the points in a conﬁguration like this makes

the nature of the patterning obvious.

Interpretation of the multidimensional scaling of the Ixcaquixtla household units

is considerably more complicated. In the ﬁrst place, the conﬁguration we need to

interpret is not in two dimensions, but in three. It is usually easiest to see three-

dimensional conﬁgurations in three views based on each pair of the three dimensions

taken two at a time. If the three-dimensional conﬁguration is imagined in real space,

it would take the form of a cube with points scattered around in it. The cube could be

looked at in perspective from an angle, and most statpacks will produce such a plot,

but it can be very difﬁcult to see just where the points really are in relation to each

other. It is often clearer to look at the cube successively from three different sides:

ﬁrst, directly from the front; second, directly from one side; and third, directly from

the top. This is how we will inspect the three-dimensional conﬁguration produced

from the Ixcaquixtla household data.

Figure 23.2. Two-dimensional scaling conﬁguration based on distances between cities.

290 CHAPTER 23

A second complexity in this analysis is that labeling the household units with

their numbers would not automatically make any patterning clear. The simple act of

labeling the cities in Fig.

23.2 makes the patterning clear because we know where

they are, and we immediately recognize that they have been placed in their actual

spatial locations. We have no prior knowledge of, say, Household Unit 6 that makes

such pattern recognition possible. In a case like this, the most useful strategy is likely

to be looking at the behavior of each variable, one at a time, in the space deﬁned by

the three-dimensional conﬁguration.

Figure

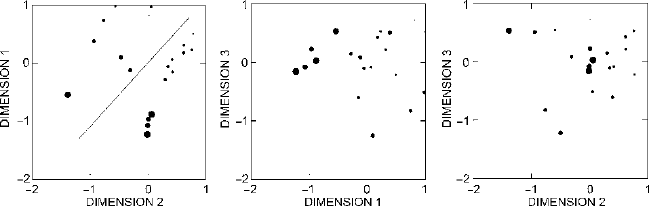
23.3 begins this process. The cube of the three-dimensional conﬁguration

is looked at in the form of three plots. The ﬁrst looks directly along the third dimen-

sion, to give a clear orthogonal view of the conﬁguration of points in Dimensions

1 and 2. The second takes a view directly along the second dimension, showing

the conﬁguration in Dimensions 1 and 3. And the third takes a view directly along

the ﬁrst dimension, giving a clear view of Dimensions 2 and 3. To envision the full

three-dimensional conﬁguration as a cube, imagine cutting out the leftmost plot in

Fig.

23.3 and pasting it to the top of the cube. Then cut out the center plot and paste

it to the left side of the cube. The rightmost plot would go on the front of the cube.

Together the three plots make it possible to look at the cube in all its dimensions.

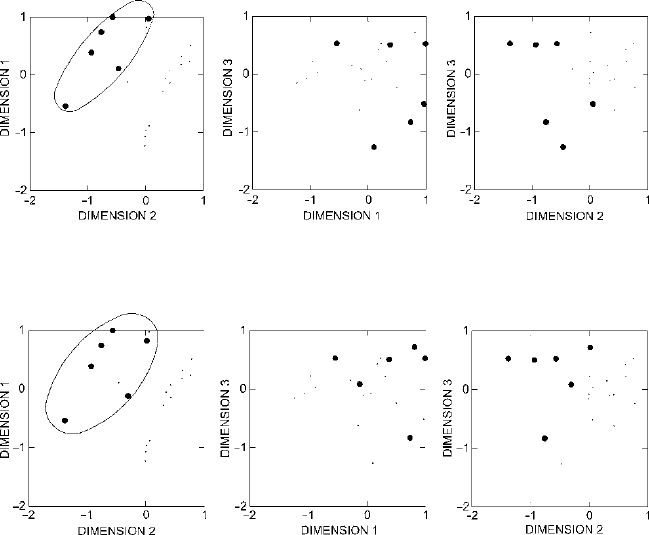
Within the plots in Fig.

23.3, each circle represents one household, and larger circles

correspond to higher values of the ﬁrst variable in the dataset, Bowls as % of Sherds.

A clear trend is visible in the plot of Dimensions 1 and 2. The values of Bowls as

% of Sherds are quite low in the upper right corner of this plot and increase steadily

toward the lower left. Household units with high proportions of bowls, then, appear

toward the lower left of the plot of Dimensions 1 and 2.

Figure

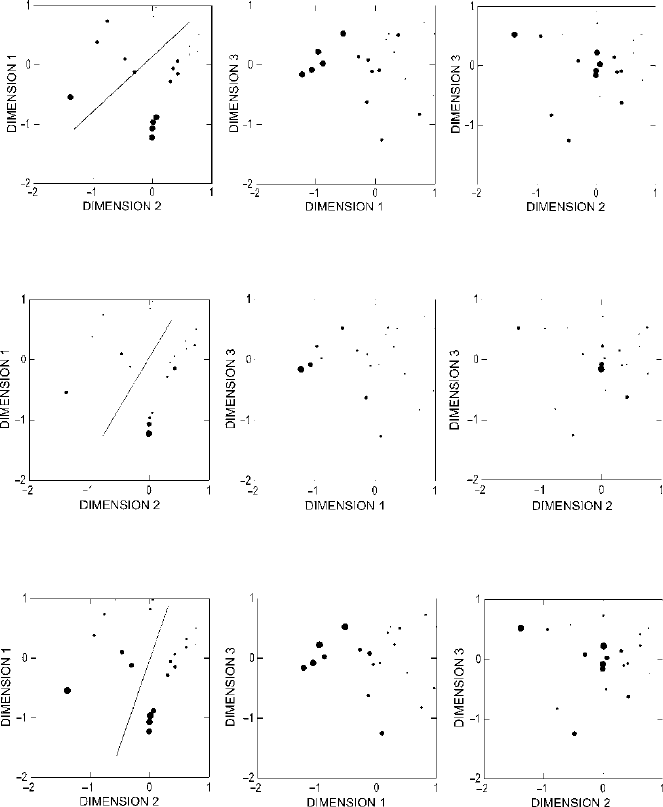
23.4 provides the same kind of illustration of Energy Invested in Burials,

and again we see the same pattern. Households with the highest levels of energy

invested in burials on average appear toward the lower left corner of the plot of

Dimensions 1 and 2. Continuing with Fig.

23.5, we see a pattern for Decoration

as % of Sherds that is not identical, but very similar to that seen for the two vari-

ables shown in Figs.

23.3 and 23.4. Household units with the highest proportions

of decorated ceramics appear toward the bottom and slightly toward the left in the

plot of Dimensions 1 and 2. The Fauna/Sherd Ratio shows the same pattern yet

Figure 23.3. Plots of the three-dimensional scaling of Ixcaquixtla household data (larger circles

indicate higher proportions of bowls).

MULTIDIMENSIONAL SCALING 291

Figure 23.4. Plots of the three-dimensional scaling of Ixcaquixtla household data (larger circles

indicate greater energy investment in burials).

Figure 23.5. Plots of the three-dimensional scaling of Ixcaquixtla household data (larger circles

indicate higher proportions of decorated ceramics).

Figure 23.6. Plots of the three-dimensional scaling of Ixcaquixtla household data (larger circles

indicate higher proportions of faunal remains).

again: higher values toward the bottom and slightly toward the left in the plot of

Dimensions 1 and 2 in Fig.

23.6.

These four variables, then, pattern in the same way in the space deﬁned by the

three-dimensional conﬁguration. Households where the value of one of these vari-

ables is high tend strongly to be households where the values of the others are also

high. The four variables form a gradient running roughly from the upper right to

the lower left in the plot of Dimensions 1 and 2. Values for proportion of bowls,

292 CHAPTER 23

for energy investment in burials, for proportion of decorated ceramics, and for the

ratio of faunal remains to sherds increase in a more or less gradual fashion along

this gradient. None of the other variables, as we shall see, pattern in this way. The

description up to this point is of the patterning to be observed in the dataset, and

it is clearly shown in the plots of these variables in the multidimensional scaling

space. The next step takes us from the realm of ﬁnding patterning through multi-

variate analysis into the realm of interpretation. We might interpret this pattern as

reﬂecting a dimension of economic differentiation at Ixcaquixtla. All four variables

might plausibly be connected to economic well-being or standard of living. All four

pattern in the same way, suggesting a gradient of wealth from low to high.

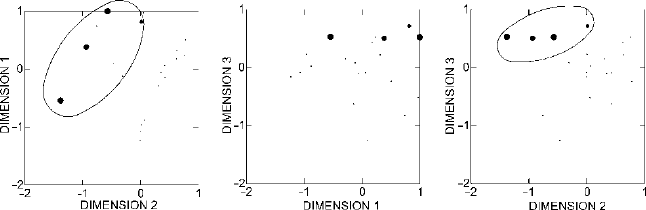
Moving on through the variables, Platform also shows a clear pattern in the plot

of Dimensions 1 and 2 in Fig.

23.7, but it is a distinctly different pattern from the

one we have been seeing. High values for Platform are clustered toward the upper

left. Since Platform is a presence/absence variable, high values (large circles) mean

the code for presence (1) and low values (small circles) mean the code for absence

(0). The other presence/absence variable, Mace Heads, shows a very similar pattern

in Fig.

23.8. Again as the inevitable result of being a presence/absence variable the

pattern looks more like a cluster than a gradient. Closer comparison of Figs.

23.7 and

Figure 23.7. Plots of the three-dimensional scaling of Ixcaquixtla household data (larger circles

indicate house structures built on platforms).

Figure 23.8. Plots of the three-dimensional scaling of Ixcaquixtla household data (larger circles

indicate presence of maces in burials).

MULTIDIMENSIONAL SCALING 293

Figure 23.9. Plots of the three-dimensional scaling of Ixcaquixtla household data (larger circles

indicate higher proportions of marine shell).

23.8 shows that this pattern is actually a bit more like a gradient than it ﬁrst appears.

Farthest off to the upper left are four household units where the house structure is

built on a platform and where mace heads are present in burials. Not so far toward

the upper left are two households with platforms but no mace heads and two with

mace heads but no platforms. At the opposite end of the scale is a larger number of

households with neither platforms nor mace heads. These are toward the lower right

in the plot of Dimensions 1 and 2.

There is, then, another gradient running perpendicular to the one apparent in

Figs.

23.3–23.6. Since they are perpendicular, the two are unrelated to each other.

Some households with platforms and mace heads are toward the wealthier end of

the ﬁrst gradient; others are not. In this way Figs.

23.7 and 23.8 delineate a sec-

ond separate and independent element of patterning in the multidimensional space.

The patterning is again quite clear, although as always open to potentially different

interpretations. We might interpret this second gradient as one of prestige or pos-

sibly political authority, which at Ixcaquixtla seems not to correspond to wealth.

However we interpret these two gradients in the multidimensional space, both their

presence and their independence are clear patterns in the scaling results.

The patterns we have discussed up to this point have been most visible in the

plot of Dimensions 1 and 2. We have not yet needed to look at the cube from any

other angle. A few household units with high proportions of marine shell, how-

ever, can be seen to cluster clearly together in the plot of Dimensions 2 and 3 in

Fig.

23.9. They also form a detectable cluster in the plot of Dimensions 1 and 2,

although this cluster is less clear, since it also includes some households without

high proportions of shell. This pattern simultaneously suggests both some relation

with the gradient identiﬁed in Figs.

23.7 and 23.8 and some independence from it.

A few households with high proportions of obsidian also cluster together in the plot

of Dimensions 2 and 3 in Fig.

23.10, but this cluster is not in the same place as the

cluster of household units with high proportions of shell. The cluster of households

with high proportions of obsidian can also be observed in the plot of Dimensions

1 and 3. Households with high proportions of obsidian also focus in the upper left

of the plot of Dimensions 1 and 2, but they are more mixed there with households

having low proportions of obsidian. If high proportions of marine shell and obsid-