Dougherty С. Introduction to Econometrics, 3Ed

Подождите немного. Документ загружается.

MULTIPLE REGRESSION ANALYSIS

Using (4.5), we can write

∑∑

−−−==

iii

XbXbbYeRSS

33221

)( (4.6)

The first-order conditions for a minimum,

∂

RSS

∂

RSS

, and

∂

RSS

, yield the

following equations:

0)(2

33221

=−−−−=

∂

∑

iii

XbXbbY

RSS

(4.7)

0)(2

332212

=−−−−=

∂

∑

iiii

XbXbbYX

RSS

(4.8)

0)(2

332213

=−−−−=

∂

∑

iiii

XbXbbYX

RSS

(4.9)

Hence we have three equations in the three unknowns,

, and

. The first can easily be

rearranged to express

in terms of

, and the data on

, and

33221

XbXbYb

−−=

. (4.10)

Using this expression and the other two equations, with a little work one can obtain the following

expression for

3232

32332

)],(Cov[)(Var)(Var

),(Cov),(Cov)(Var),(Cov

XXXX

XXYXXYX

−

(4.11)

A parallel expression for

can be obtained by interchanging

and

in (4.11).

The intention of this discussion is to press home two basic points. First, the principles behind the

derivation of the regression coefficients are the same for multiple regression as for simple regression.

Second, the expressions, however, are different, and so you should not try to use expressions derived

for simple regression in a multiple regression context.

The General Model

In the preceding example, we were dealing with only two explanatory variables. When there are more

than two, it is no longer possible to give a geometrical representation of what is going on, but the

extension of the algebra is in principle quite straightforward.

We assume that a variable

depends on

– 1 explanatory variables

, ...,

according to a true,

unknown relationship

MULTIPLE REGRESSION ANALYSIS

+ … +

+ u

. (4.12)

Given a set of n observations on Y, X

, ..., X

, we use least squares regression analysis to fit the

equation

kikii

XbXbbY

+++=

...

221

(4.13)

This again means minimizing the sum of the squares of the residuals, which are given by

kikiiiii

XbXbbYYYe

−−−−=−=

...

221

(4.14)

(4.14) is the generalization of (4.5). We now choose b

, ..., b

so as to minimize RSS, the sum of the

squares of the residuals,

∑

. We obtain k first order conditions

∂

RSS

, …,

∂

RSS

, and

these provide k equations for solving for the k unknowns. It can readily be shown that the first of

these equations yields a counterpart to (4.10) in the case with two explanatory variables:

XbXbYb

−−−=

...

221

. (4.15)

The expressions for b

, ..., b

become very complicated and the mathematics will not be presented

explicitly here. The analysis should be done with matrix algebra.

Whatever Happened to

You may have noticed that X

is missing from the general regression model

+ … +

+ u

Why so? The reason is to make the notation consistent with that found in texts using

linear algebra (matrix algebra), and your next course in econometrics will almost

certainly use such a text. For analysis using linear algebra, it is essential that every ter

on the right side of the equation should consist of the product of a parameter and a

variable. When there is an intercept in the model, as here, the anomaly is dealt with by

writing the equation

+ … +

+ u

where X

is equal to 1 in every observation. In analysis using ordinary algebra, there is

usually no point in introducing X

explicitly, and so it has been suppressed. The one

occasion in this text where it can help is in the discussion of the dummy variable trap in

Chapter 6.

MULTIPLE REGRESSION ANALYSIS

Interpretation of the Multiple Regression Coefficients

Multiple regression analysis allows one to discriminate between the effects of the explanatory

variables, making allowance for the fact that they may be correlated. The regression coefficient of

each X variable provides an estimate of its influence on Y, controlling for the effects of all the other X

variables.

This can be demonstrated in two ways. One is to show that the estimators are unbiased, if the

model is correctly specified and the Gauss–Markov conditions are fulfilled. We shall do this in the

next section for the case where there are only two explanatory variables. A second method is to run a

simple regression of Y on one of the X variables, having first purged both Y and the X variable of the

components that could be accounted for by the other explanatory variables. The estimate of the slope

coefficient and its standard error thus obtained are exactly the same as in the multiple regression. It

follows that a scatter diagram plotting the purged Y against the purged X variable will provide a valid

graphical representation of their relationship that can be obtained in no other way. This result will not

be proved but it will be illustrated using the earnings function in Section 4.1:

EARNINGS =

S +

ASVABC + u. (4.16)

Suppose that we are particularly interested in the relationship between earnings and schooling and that

we would like to illustrate it graphically. A straightforward plot of EARNINGS on S, as in Figure 2.8,

would give a distorted view of the relationship because ASVABC is positively correlated with S. As a

consequence, as S increases, (1) EARNINGS will tend to increase, because

is positive; (2) ASVABC

will tend to increase, because S and ASVABC are positively correlated; and (3) EARNINGS will

receive a boost due to the increase in ASVABC and the fact that

is positive. In other words, the

variations in EARNINGS will exaggerate the apparent influence of S because in part they will be due

to associated variations in ASVABC. As a consequence, in a simple regression the estimator of

will

be biased. We will investigate the bias analytically in Section 7.2.

In this example, there is only one other explanatory variable, ASVABC. To purge EARNINGS and

S of their ASVABC components, we first regress them on ASVABC:

ASVABCccINGSNEAR

(4.17)

ASVABCddS

(4.18)

We then subtract the fitted values from the actual values:

INGSNEAREARNINGSEEARN

−=

(4.19)

SSES

−=

(4.20)

The purged variables EEARN and ES are of course just the residuals from the regressions (4.17)

and (4.18). We now regress EEARN on ES and obtain the output shown.

MULTIPLE REGRESSION ANALYSIS

. reg EEARN ES

Source | SS df MS Number of obs = 570

---------+------------------------------ F( 1, 568) = 21.21

Model | 1256.44239 1 1256.44239 Prob > F = 0.0000

Residual | 33651.2873 568 59.2452241 R-squared = 0.0360

---------+------------------------------ Adj R-squared = 0.0343

Total | 34907.7297 569 61.3492613 Root MSE = 7.6971

------------------------------------------------------------------------------

EEARN | Coef. Std. Err. t P>|t| [95% Conf. Interval]

---------+--------------------------------------------------------------------

ES | .7390366 .1604802 4.605 0.000 .4238296 1.054244

_cons | -5.99e-09 .3223957 0.000 1.000 -.6332333 .6332333

------------------------------------------------------------------------------

You can verify that the coefficient of ES is identical to that of S in the multiple regression in

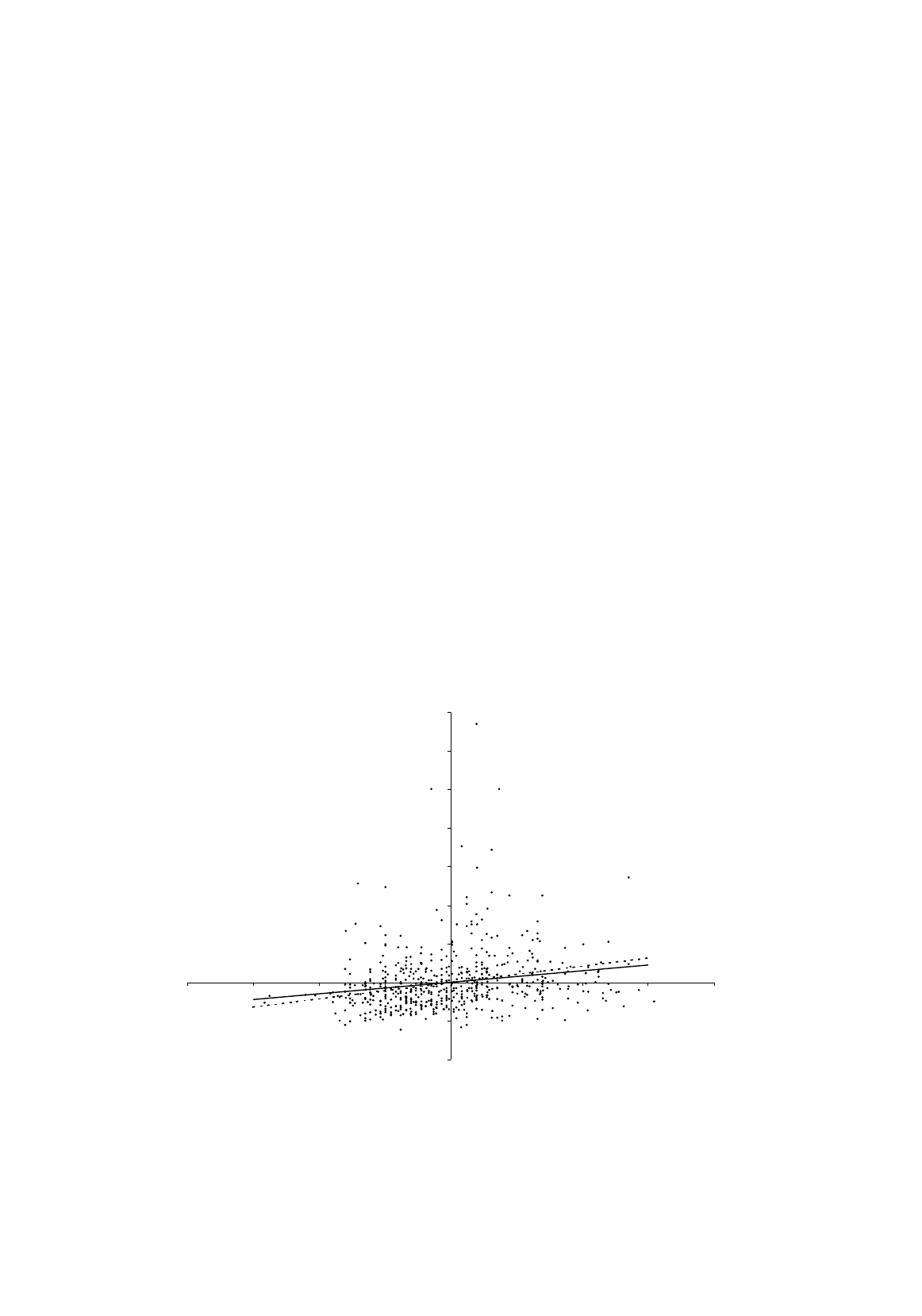
Section 4.1. Figure 4.2 shows the regression line in a scatter diagram. The dotted line in the figure is

the regression line from a simple regression of EARNINGS on S, shown for comparison.

The estimate of the intercept in the regression uses a common convention for fitting very large

numbers or very small ones into a predefined field. e +n indicates that the coefficient should be

multiplied by 10

. Similarly e –n indicates that it should be multiplied by 10

–

. Thus in this regression

the intercept is effectively 0.

Figure 4.2.

Regression of

EARNINGS

residuals on

residuals

-20

-10

-8 -6 -4 -2 0 2 4 6 8

EEARN

MULTIPLE REGRESSION ANALYSIS

Exercises

4.1

The result of fitting an educational attainment function, regressing S on ASVABC, SM, and SF,

years of schooling (highest grade completed) of the respondent’s mother and father,

respectively, using EAEF Data Set 21 is shown below. Give an interpretation of the regression

coefficients.

. reg S ASVABC SM SF

Source | SS df MS Number of obs = 570

---------+------------------------------ F( 3, 566) = 110.83

Model | 1278.24153 3 426.080508 Prob > F = 0.0000

Residual | 2176.00584 566 3.84453329 R-squared = 0.3700

---------+------------------------------ Adj R-squared = 0.3667

Total | 3454.24737 569 6.07073351 Root MSE = 1.9607

------------------------------------------------------------------------------

S | Coef. Std. Err. t P>|t| [95% Conf. Interval]

---------+--------------------------------------------------------------------

ASVABC | .1295006 .0099544 13.009 0.000 .1099486 .1490527

SM | .069403 .0422974 1.641 0.101 -.013676 .152482

SF | .1102684 .0311948 3.535 0.000 .0489967 .1715401

_cons | 4.914654 .5063527 9.706 0.000 3.920094 5.909214

------------------------------------------------------------------------------

4.2

Fit an educational attainment function parallel to that in Exercise 4.1, using your EAEF data set,

and give an interpretation of the coefficients.

4.3

Fit an earnings function parallel to that in Section 4.1, using your EAEF data set, and give an

interpretation of the coefficients.

4.4

Using your EAEF data set, make a graphical representation of the relationship between S and

SM using the technique described above, assuming that the true model is as in Exercise 4.2. To

do this, regress S on ASVABC and SF and save the residuals. Do the same with SM. Plot the S

and SM residuals. Also regress the former on the latter, and verify that the slope coefficient is

the same as that obtained in Exercise 4.2.

4.5*

Explain why the intercept in the regression of EEARN on ES is equal to 0.

4.3 Properties of the Multiple Regression Coefficients

As in the case of simple regression analysis, the regression coefficients should be thought of as special

kinds of random variables whose random components are attributable to the presence of the

disturbance term in the model. Each regression coefficient is calculated as a function of the values of

Y and the explanatory variables in the sample, and Y in turn is determined by the explanatory variables

and the disturbance term. It follows that the regression coefficients are really determined by the

values of the explanatory variables and the disturbance term and that their properties depend critically

upon the properties of the latter.

We shall continue to assume that the Gauss–Markov conditions are satisfied, namely (1) that the

expected value of u in any observation is 0, (2) that the population variance of its distribution is the

same for all observations, (3) that the population covariance of its values in any two observations is 0,

and (4) that it is distributed independently of any explanatory variable. The first three conditions are

MULTIPLE REGRESSION ANALYSIS

the same as for simple regression analysis and (4) is a generalization of its counterpart. For the time

being we shall adopt a stronger version of (4) and assume that the explanatory variables are

nonstochastic.

There are two further practical requirements. First, there must be enough data to fit the regression

line; that is, there must be at least as many (independent) observations as there are parameters to be

estimated. Second, as we shall see in Section 4.4, there must not be an exact linear relationship among

the explanatory variables.

Unbiasedness

We will first show that b

is an unbiased estimator of

in the case where there are two explanatory

variables. The proof can easily be generalized, using matrix algebra, to any number of explanatory

variables. As one can see from (4.11), b

is calculated as a function of X

, X

, and Y. Y in turn is

generated by X

, X

, and u. Hence b

depends in fact on the values of X

, X

and u in the sample

(provided that you understand what is going on, you may skip the details of the mathematical

working):













+++−

+++

∆













+++−

+++

∆

−

),(Cov)],(Cov),(Cov),(Cov),(Cov[

)(Var)],(Cov),(Cov),(Cov),([Cov

),(Cov])[,(Cov

)(Var])[,(Cov

)],(Cov[)(Var)(Var

),(Cov),(Cov)(Var),(Cov

32333322313

3233222212

32332213

3332212

3232

32332

XXuXXXXXX

XuXXXXXX

XXuXXX

XuXXX

XXXX

XXYXXYX

(4.21)

where

∆

is Var(X

)Var(X

) – [Cov(X

, X

)]

. Cov(X

) and Cov(X

) are both 0, using Covariance

Rule 3, because

is a constant. Cov(X

) is

Var(X

), using Covariance Rule 2 and the fact that

Cov(X

, X

) is the same as Var(X

). Similarly Cov(X

) is

Var(X

). Hence

()

[]

),(Cov),(Cov)(Var),(Cov

)],([Cov)(Var)(Var

),(Cov),(Cov),(Cov)(Var)],([Cov

)(Var),(Cov)(Var),(Cov)(Var)(Var

),(Cov)],(Cov)(Var),(Cov[

)(Var)],(Cov),(Cov)(Var[

323322

32332

32322

3233233

322

323323322

32333322

3232322

XXuXXuX

XXXX

XXuXXXXXX

XuXXXXXX

XXuXXXX

XuXXXX

−

∆

−+∆

∆





















−+

−

∆





















−−−

∆













++−

∆

(4.22)

Thus b

has two components: the true value

and an error component. If we take expectations, we

have

MULTIPLE REGRESSION ANALYSIS

3322322

)],(Cov[),(Cov

)],(Cov[)(Var

)(

∆

−

∆

uXEXXuXEXbE

(4.23)

provided that

and

are nonstochastic. (The proof that

[Cov(

)] and

[Cov(

)] are 0 is

parallel to that for

[Cov(

)] being 0 in Chapter 3.)

Efficiency

The Gauss–Markov theorem proves that, for multiple regression analysis, as for simple regression

analysis, the ordinary least squares (OLS) technique yields the most efficient linear estimators, in the

sense that it is impossible to find other unbiased estimators with lower variances, using the same

sample information, provided that the Gauss–Markov conditions are satisfied. We will not attempt to

prove this theorem since matrix algebra is required.

Precision of the Multiple Regression Coefficients

We will investigate the factors governing the likely precision of the regression coefficients for the case

where there are two explanatory variables. Similar considerations apply in the more general case, but

with more than two variables the analysis becomes complex and one needs to switch to matrix algebra.

If the true relationship is

, (4.24)

and you fit the regression line

, (4.25)

using appropriate data,

, the population variance of the probability distribution of

, is given by

)(Var

−

×=

(4.26)

where

is the population variance of

and

is the correlation between

and

. A parallel

expression may be obtained for the population variance of

, replacing Var(

) with Var(

From (4.26) you can see that, as in the case of simple regression analysis, it is desirable for

and

Var(

) to be large and for

to be small. However, we now have the further term )1(

−

and

clearly it is desirable that the correlation between

and

should be low.

MULTIPLE REGRESSION ANALYSIS

It is easy to give an intuitive explanation of this. The greater the correlation, the harder it is to

discriminate between the effects of the explanatory variables on Y, and the less accurate will be the

regression estimates. This can be a serious problem and it is discussed in the next section.

The standard deviation of the distribution of b

is the square root of the variance. As in the

simple regression case, the standard error of b

is the estimate of the standard deviation. For this we

need to estimate

. The variance of the residuals provides a biased estimator:

[]

)(Var

−

(4.27)

where k is the number of parameters in the regression equation. However, we can obtain an unbiased

estimator,

s , by neutralizing the bias:

)(Var

−

(4.28)

The standard error is then given by

)(Var

)s.e.(

−

×=

(4.29)

The determinants of the standard error will be illustrated by comparing them in earnings functions

fitted to two subsamples of the respondents in EAEF Data Set 21, those who reported that their wages

were set by collective bargaining and the remainder. Regression output for the two subsamples is

shown below. In Stata, subsamples may be selected by adding an “if” expression to a command.

COLLBARG is a variable in the data set defined to be 1 for the collective bargaining subsample and 0

for the others. Note that in tests for equality, Stata requires the = sign to be duplicated.

. reg EARNINGS S ASVABC if COLLBARG==1

Source | SS df MS Number of obs = 63

---------+------------------------------ F( 2, 60) = 2.58

Model | 172.902083 2 86.4510417 Prob > F = 0.0844

Residual | 2012.88504 60 33.5480841 R-squared = 0.0791

---------+------------------------------ Adj R-squared = 0.0484

Total | 2185.78713 62 35.2546311 Root MSE = 5.7921

------------------------------------------------------------------------------

EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval]

---------+--------------------------------------------------------------------

S | -.3872787 .3530145 -1.097 0.277 -1.093413 .3188555

ASVABC | .2309133 .1019211 2.266 0.027 .0270407 .4347858

_cons | 8.291716 4.869209 1.703 0.094 -1.448152 18.03158

------------------------------------------------------------------------------

MULTIPLE REGRESSION ANALYSIS

. reg EARNINGS S ASVABC if COLLBARG==0

Source | SS df MS Number of obs = 507

---------+------------------------------ F( 2, 504) = 40.31

Model | 4966.96516 2 2483.48258 Prob > F = 0.0000

Residual | 31052.2066 504 61.6115211 R-squared = 0.1379

---------+------------------------------ Adj R-squared = 0.1345

Total | 36019.1718 506 71.184134 Root MSE = 7.8493

------------------------------------------------------------------------------

EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval]

---------+--------------------------------------------------------------------

S | .8891909 .1741617 5.106 0.000 .5470186 1.231363

ASVABC | .1398727 .0461806 3.029 0.003 .0491425 .2306029

_cons | -6.100961 2.15968 -2.825 0.005 -10.34404 -1.857877

------------------------------------------------------------------------------

The standard error of the coefficient of S is 0.1742 in the first regression and 0.3530, twice as

large, in the second. We will investigate the reasons for the difference. It will be convenient to

rewrite (4.29) in such a way as to isolate the contributions of the various factors:

)(Var

)(s.e.

−

×××=

(4.30)

The first element we need, s

, can be obtained directly from the regression output.

s is equal to the

sum of the squares of the residuals divided by n – k, here n – 3:

RSS

nkn

−

=−×

−

∑∑

)(

)(Var

(4.31)

(Note that

is equal to 0. This was proved for the simple regression model in Chapter 3, and the

proof generalizes easily.) RSS is given in the top left quarter of the regression output, as part of the

decomposition of the total sum of squares into the explained sum of squares (in the Stata output

denoted the model sum of squares) and the residual sum of squares. The value of n – k is given to the

right of RSS, and the ratio RSS/(n – k) to the right of that. The square root, s

, is listed as the Root

MSE (root mean square error) in the top right quarter of the regression output, 5.7921 for the

collective bargaining subsample and 7.8493 for the regression with the other respondents.

ABLE

4.1

Decomposition of the Standard Error of

Component s

nVar(S)r

S,ASVABC

s.e.

Collective bargaining 5.7921 63 6.0136 0.5380 0.3530

Not collective bargaining 7.8493 507 6.0645 0.5826 0.1742

Factor

Collective bargaining 5.7921 0.1260 0.4078 1.1863 0.3531

Not collective bargaining 7.8493 0.0444 0.4061 1.2304 0.1741

MULTIPLE REGRESSION ANALYSIS

The number of observations, 63 in the first regression and 507 in the second, is also listed in the

top right quarter of the regression output. The variances of S, 6.0136 and 6.0645, had to be calculated

from the sample data. The correlations between S and ASVABC, 0.5380 and 0.5826 respectively, were

calculated using the Stata “cor” command. The factors of the standard error in equation (4.30) were

then derived and are shown in the lower half of Table 4.1.

It can be seen that, in this example, the reason that the standard error of S in the collective

bargaining subsample is relatively large is that the number of observations in that subsample is

relatively small. The effect of the variance of S is neutral, and those of the other two factors are in the

opposite direction, but not enough to make much difference.

t Tests and Confidence Intervals

t tests on the regression coefficients are performed in the same way as for simple regression analysis.

Note that when you are looking up the critical level of t at any given significance level, it will depend

on the number of degrees of freedom, n – k: the number of observations minus the number of

parameters estimated. The confidence intervals are also constructed in exactly the same way as in

simple regression analysis, subject to the above comment about the number of degrees of freedom. As

can be seen from the regression output, Stata automatically calculates confidence intervals for the

coefficients (95 percent by default, other levels if desired), but this is not a standard feature of

regression applications.

Consistency

Provided that the fourth Gauss–Markov condition is satisfied, OLS yields consistent estimates in the

multiple regression model, as in the simple regression model. As n becomes large, the population

variance of the estimator of each regression coefficient tends to 0 and the distribution collapses to a

spike, one condition for consistency. Since the estimator is unbiased, the spike is located at the true

value, the other condition for consistency.

Exercises

4.6

Perform t tests on the coefficients of the variables in the educational attainment function

reported in Exercise 4.1.

4.7

Perform t tests on the coefficients of the variables in the educational attainment and earnings

functions fitted by you in Exercises 4.2 and 4.3.

4.8

The following earnings functions were fitted separately for males and females, using EAEF

Data Set 21 (standard errors in parentheses):

males

INGSNEAR

= –3.6121 + 0.7499S + 0.1558ASVABC

(2.8420) (0.2434) (0.0600)