Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry
Подождите немного. Документ загружается.


492 CONFORMAL OPERATORS CHAPTER 16
TRSversorLog log(const TRSversor &V) {
// get rotor part:
rotor X = _rotor( — no << (V * ni));
const float EPSILON = 1e — 6f;
// get scaling part
mv::Float gamma = (mv::Float)::log(_Float(X * reverse(X)));
mv::Float gammaPrime;
if (fabs(gamma) < EPSILON) gammaPrime = 1.0f;
else gammaPrime = gamma / (::exp(gamma) — 1);
scalor S = exp(_noni_t(0.5f * gamma * noni));
// get rotation part
rotor R = _rotor(::exp( — 0.5f * gamma) * X);
// get translation part:
translator T = _translator(V * reverse(S) * reverse(R));
vectorE3GA t = _vectorE3GA( — 2.0f * (no << T));
if (_Float(norm_e2(_bivector E3GA (R))) < EPSILON * EPSILON) {
if (_Float(R) > 0.0f) { //R=1
// no rotation, so no rotation plane
return _TRSversorLog((0.5f * ( — gammaPrime * (t ^ ni) + gamma * noni));
}
else { //R=—1
// We need to add a 360 degree rotation to the result.
// Take it perpendicular to ’t’:
bivectorE3GA I; // Get a rotation plane ’I’, depending on ’t’
if (_Float(norm_e_2(t)) > EPSILON * EPSILON)
I = _bivectorE3GA(unit_e(t << I3));
else I = _bivectorE3GA(e1^e2); //whent=0,anyplane will do
return _TRSvectorLog(0.5f * (
— gammaPrime * (t ^ ni) +
gamma * noni +
2.0f * (
float) M_PI * I));
}
}
else {
// get rotation plane, angle
bivectorE3GA I = _bivectorE3GA(R);
mv::Float sR2 = _Float(norm_e(I));
I = _bivectorE3GA(I * (1.0f / sR2));
mv::Float phi = — 2.0f * (mv::Float)atan2(sR2, _Float(R));
Continued

SECTION16.10 PROGRAMMING EXAMPLES AND EXERCISES 493
(continued)
// form bivector log of versor:
normalizedTranslator Tv = _normalizedTranslator(
1.0f — 0.5f * inverse(1.0f — (mv::Float)::exp(gamma)*R*R)*
(t << I) * reverse(I) * ni);
return _TRSversorLog(0.5f * ( — gammaPrime * (t^I) * reverse(I) * ni +
( — gammaPrime * (t^I) * reverse(I) * ni +
Tv*(—phi*I+gamma * noni) * reverse(Tv)));
}
}
Figure 16.15: Logarithm of scaled rigid body motion (Example 2). This function returns the logarithm of normalized
translate-rotate-scale (TRS) versors.
We will show in Chapter 22 that for a ray-tracing application, the speed of an efficiently
implemented conformal model is the same as for the homogeneous coordinate approach.
Therefore, criteria such as expressibility of the operations or ease of programming can be
the deciding factors.
16.10.2 LOGARITHM OF SCALED RIGID BODY MOTION
The code for computing the logar ithm of a TRSversor (t ranslate-rotate-scale-versor)
is shown in Figure 16.15. It is a straightforward implementation of the pseudocode in
Figure 16.5 in Section 16.3.4. The function resides in
c3ga_util.cpp. Note that the func-
tion returns the
TRSversorLog type, which is a specialized multivector type (the basis
blades are
e1∧e2, e1∧e3, e2∧e3, e1∧ni, e2∧ni, e3∧ni, and no∧ni). The example itself
just tests the
log() code by repeatedly generating random TRS versors V and checking
that
V = exp(log(V)).
16.10.3 INTERPOLATION OF SCALED RIGID BODY MOTIONS
We now revisit the interpolation examples from Sections 10.7.1 and 13.10.4, this time
adding the scalability. We interpolate from one random TRS versor to the next. The ran-
dom versors are created as follows:
void initRandomDest() {
// get two random translators, a random rotor and a random scalor:
normalizedTranslator T1 = exp(_freeVector(randomBlade(2, 3.0f)));
normalizedTranslator T2 = exp(_freeVector(randomBlade(2, 3.0f)));
rotor R = exp(_bivectorE3GA(randomBlade(2, 100.0f)));
mv::Float s1 = (mv::Float)(1 + rand()) / (mv::Float)(RAND_MAX/2);
scalor S1 = exp(_noni_t(0.5f * log(s1) * noni));
494 CONFORMAL OPERATORS CHAPTER 16
// return a random TRS versor:
g_destVersor = _TRSversor(T1 * S1 * T2*R*inverse(T2));
}
Using the log() function from the previous example, the interpolation code requires
little change compared to previous version:
TRSversor interpolateTRSversor(const TRSversor &src, const
TRSversor &dst, mv::Float alpha) {
// return src * exp(alpha * log(inverse(src) * dst));
return _TRSversor(src * exp(_TRSversor(alpha *
log(_TRSversor(inverse(src) * dst)))));
}
16.10.4 THE SEASHELL
This example code reproduces Figure 16.3. You can drag the outermost circle and sphere
around to produce variations of the figure. A screenshot is shown in Figure 16.16. The
code to draw the shell is
// Create versor that generates the sea shell:
TRSversor V = _TRSversor((1.0f — 0.25f * e3ni) *
exp(_bivectorE3GA((e1^e2) * 0.4f)) *
exp(_noni_t( — 0.05f * noni)));
// Take 1/5st of the versor:
V = exp(0.2f * log(V)); // take only 1/5st of the versor
// precompute inverse of the versor:
TRSversor Vi = _TRSversor(inverse(V));
// get the circle:
circle C = g_circle;
// draw the circles:
const int NB_ITER = 200;
for (int i = 0; i < NB_ITER; i++) {
draw(C);
// update circle such that we draw a ’trail’ of circles
C=V*C*Vi;
}
// get the sphere:
sphere S = g_sphere;
// draw spheres:
for (int i = 0; i < NB_ITER; i++) {
draw(S);
// update sphere such that we draw a ’trail’ of spheres
S=V*S*Vi;
}
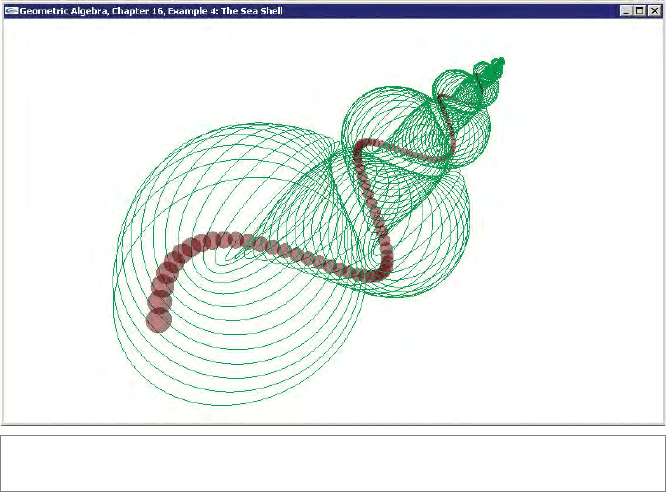
SECTION16.10 PROGRAMMING EXAMPLES AND EXERCISES 495
Figure 16.16: Screenshot of Example 4.
17
OPERATIONAL MODELS
FOR GEOMETRIES
Now that we have the conformal model of Euclidean geometry and have seen its
effectiveness, it is useful to take a step back and look in a more abstract manner at
what we have actually done and why it works so well. That will provide a tentative
glimpse of future developments in this way of encoding geometries.
17.1 ALGEBRAS FOR GEOMETRIES
A geometry (affine, Euclidean, conformal, projective, or any kind) is characterized by
certain operators that act on the objects of the geometry. These objects can range from
geometrical entities such as a triangle to properties such as length, so they may have
various dimensionalities (which we call grades). The operators in the geometry change
these objects in a covariant manner, preserving their structure in the following sense. The
transformation V[A ◦ B]ofanobjectconstructedfromA and B as A ◦ B (using some
constructor product ◦) should transform to V[A] ◦ V[B]:
covariance: V[A ◦ B] = V[A] ◦ V[B].
(17.1)
These essential operators defining the geometry are sometimes called symmetries.
A convenient algebraic system encodes the operators so deeply into its framework that
such covariant identities hold trivially. Conversely, only elements that transform in this
497
498 OPERATIONAL MODELS FOR GEOMETRIES CHAPTER 17
manner deserve to be considered as objects in the geometry. Other elements fall apart
under the transformations, and thus have no permanence of their defining properties.
Geometric algebra offers a method to produce such an automatically covariant
representation system. Two features are essential for this:
•
The two-sided versor product preserves the geometric product structure
V (XY) V
−1
= (VXV
−1
)(VYV)
−1
.
Since the geometric product encodes the metric, a versor represents an orthogonal
transformation.
•
All geometrical constructions can be expressed in terms of the geometric product,
both for objects and operators. (This can be done as linear combinations, or by
grade selection; we have used both.)
In order to use this structural capability for a given geometry, we need to find a good rep-
resentational space of which we then use the geometric algebra. In this representational
space, the symmetries should become isometries. Isometries are distance-preserving trans-
formations; they are the orthogonal transfor mations in the representational space that
can be represented by versors in the corresponding geometric algebra.
We can call such a model of geometry an operational model, since it is fully designed
around the operational symmetry that defines the geometry. An operational model is
automatically structure-preserving, so the quest for a good representation of a geometry
amounts to setting up an appropriate representational space with the proper metric to
represent the symmetry invariants of the geometry.
We have seen some examples of this process in this book, and some more are known.
•
Algebra of D irections. In the vector space model of Chapter 10, we considered
the geometry of oriented and weighted directions. The basic operations in this
geometry are the rotations, which can transform between directions. The metr ic
of the directional space is Euclidean, so that different directions can be compared in
weight (interpretable as length, velocity, area, volume, etc.). The versors we found
are reflections and rotors (the latter are n-dimensional quaternions).
•
Euclidean Geometry. Euclidean symmetries preserve Euclidean distances of points
and the point at infinity. The operational model takes this to define the metric
of the representational space. As we have seen, an isometric representation of the
Euclidean geometry is reached by embedding in a space of two more dimensions
and a Minkowski metric. One of the dimensions is used to encode the point at infin-
ity. The other is used to represent the weight of elements, a somewhat unexpected
aspect of geometry necessary for linearity of the basic operations in their algebraic
representation.
•
Conformal Geometry. In conformal geometry in general, the invariance of some
set representing the points at infinity is important. In Euclidean geometry, this is
a point; in hyperbolic geometry, a real unit sphere; and in spherical geometry, an
SECTION 17.1 ALGEBRAS FOR GEOMETRIES 499
imaginary unit sphere. The representational space that (dually) represents these
sets as vectors is the conformal model. Its distance measures are related to the
inner product through its translation versor.
•
Image Geometry. Koenderink [35] has recently proposed an image algebra for the
geometrical symmetries of images. These involve not only the spatial geometry of
the image plane, but also the transformations on the value domain, and the inter-
action between the two. This induces a combined model with a mixed geometry,
for 2-D gray value images the representation space is
R
4,2
,stratifiedasaconfor-
mal model
R
2+1,1
for the Euclidean geometry in the base plane and a conformal
model
R
1,1
for the scalar value dimension. The versors of this model give a basis for
developing spatial smoothing operators.
•
Projective Geometry. Unfortunately, there is not yet an operational model for
projective geometry. That would have projective transformations as versors
(rather than as linear transformations, as in the homogeneous coordinate
approach). The metric of the representation space should probably be based on
the cross ratio. Its blades would naturally represent the conic sections. Initial
attempts [15, 48] do not quite have this structure, but we hope an operational
projective model will be developed soon.
•
Contact Geometry. There are more special geometries that might interest us in com-
puter science. For instance, collision detection requires an efficient representation
of contact. In classical literature, symplectic geometries have been developed for this
based on canonical transformations (or contact transfor mations) [15]. It would be
very interesting to compute with those by means of their own operational models,
hopefully enabling more efficient treatment of problems like collision detection and
path planning.
•
And More. The more we delve into the mathematical literature of the 19th century,
the more geometries we find. They all make some practical sense, but only projective
geometry (and its subgeometries such as affine and Euclidean geometry) appears to
have become part of mainstream knowledge. With the common representational
framework of geometric algebra, we find that this obscure literature has become
quite readable. As we begin to read it, we find it disconcerting that many aspects
of the conformal model of Euclidean geometry pop up regularly (for instance, in
[9, 10]). We could have had this all along, and it makes us wonder what else is already
out there ...
We hope to have convinced you in Part II that the structural properties of an operational
model are nice to have. Not only do they permit universal constructions and operators,
but the y also make available the quantitative techniques of interpolation and estimation.
Linear techniques applied at the right level of the model (for instance, on the bivectors that
are the logarithms of the rotors) provide more powerful results than the same techniques
applied to the classical vectors or the matrix representations acting upon them.
It remains to show that such models are not only structurally desirable, but also efficient
in computation. We do this in Part III.
18
IMPLEMENTATION
ISSUES
In the first two parts of this book, we have given an abstract description of geometric
algebra that is mostly free of coordinates and other low-level implementation details.
Even though we have provided many programming examples, this may still have left
you with a somewhat unreal feeling about geometric algebra, and an impression that any
implementation of geometric algebra would be computationally prohibitive in a practical
application. To address these concerns, Part III gives details on how to create an efficient
numerical implementation of geometric algebra.
We describe the implementation of all products, operations, and models that were used
in the preceding parts. The description is from the viewpoint of representing multivectors
as a weighted sum of basis blades, an approach that was already hinted at in Section 2.9.4.
This is by far the most common way of implementing geometric algebra, although other
approaches are also possible. We briefly mention alternatives in Section 18.3.
Our ultimate goal is efficient numerical implementation, not symbolic computer alge-
bra. An efficient geometric algebra implementation uses symbolic manipulations only to
bootstrap the implementation, and not during actual run-time computations. We have
tried to keep the implementation description independent of any particular implemen-
tation, although Chapter 22 is basically a high-level description of how
Gaigen 2 works.
Gaigen 2 is the implementation behind the GA sandbox source code package that you
have used in the programming examples and exercises.
503

504 IMPLEMENTATION ISSUES CHAPTER 18
18.1 THE LEVELS OF GEOMETRIC ALGEBRA
IMPLEMENTATION
All multivectors can be decomposed as a sum of basis blades. An example of a basis for a
3-D geometric algebra is
1
scalars
, e
1
, e
2
, e
3
vector space
, e
1
∧ e
2
, e
2
∧ e
3
, e
3
∧ e
1
bivector space
, e
1
∧ e
2
∧ e
3
trivector space
.
The number of k-blades in a geometric algebra over an n-dimensional space is
n
k
,so
there are a total of
n
k=0
n
k
= 2
n
basis elements required to span the entire geometric algebra. On such a basis we can
represent any multivector A as a column vector [[ A]] with 2
n
elements, containing the
coefficients of A on the basis. A can be retrieved by a matrix multiply of a symbolic row
vector containing the basis elements. For the 3-D example above, this would be
A = [[ 1 , e
1
, e
2
, e
3
, e
1
∧ e
2
, e
2
∧ e
3
, e
1
∧ e
3
, e
1
∧ e
2
∧ e
3
]] [[ A]] .
A k-blade only contains elements of grade k, and therefore has many zero entries in its
coefficient vector [[ A]] , making the representation by 2
n
elements rather wasteful. This
effect becomes stronger in higher dimensions.
We should therefore explore the idea to make a more sparse representation of the elements
of geometric algebra. It can still be based in this sum of basis blades principle, just executed
with more sensitivity to the essential structure of geometric algebra.
With the sum of basis blades implementation as our core approach, a geometric algebra
implementation naturally splits into four levels:
1. Selecting the basis blades and implementing the basic operations on them;
2. Implementing linear operations for multivectors;
3. Implementing nonlinear operations on multivectors;
4. The application level.
The following chapters first describe the first three levels, then continue to provide addi-
tional detail on efficiency and implementation, and finally talk about the fourth level, as
follows:
•
Implementing Basic Operations for Basis Blades (Chapter 19). Clearly, it pays
to consider the lowest implementation level in detail. We introduce a convenient
SECTION 18.1 THE LEVELS OF GEOMETRIC ALGEBRA IMPLEMENTATION 505
representation of basis blades and show how the elementary operations have
a satisfyingly Boolean nature when considered on the basis. This will deepen
your understanding of them and leads to efficient algorithms for the most basic
computations.
•
The Linear Middle Level (Chapter 20). We then use those basic capabilities to estab-
lish the middle level. Many operations of geometric algebra are linear and distribu-
tive. This property makes their implementation quite simple, given that we can
already compute them for the basis blades. We consider implementation of this
level through matr ices (most directly exploiting the linear nature of the operators)
or by looping over lists of basis blades (which more naturally leads to an efficient
implementation).
•
The Nonlinear Level (Chapter 21). Geometric algebra contains some important
operations that are elementary, but not linear or distributive (examples are inver-
sion,
meet and join, and exponentiation). As a consequence, the approach used in
the middle-level implementation cannot be used here. These operations are imple-
mented using specialized algor ithms, which are actually largely independent of the
middle-level implementation. Only for efficiency reasons do we sometimes need
direct access to the multivector representation (e.g., to find the largest coordinate
in a numerically stable factorization algorithm).
•
Our Reference Implementation (Online). To better illustrate the implementation
ideas, we have written an accompanying reference implementation in Java based on
the list of basis blades approach. It is available at http://www.geometricalgebra.net.
This reference implementation was written for educational purposes, and it is not
the same as the GA sandbox source code package. The difference is that in our ref-
erence implementation we have favored simplicity and readability over efficiency,
so we do not recommend using it for computationally intensive applications.
•
Efficient Implementation (Chapter 22). We show how to specialize the implemen-
tation according to the structure of geometric algebra to obtain high run-time
efficiency. We also present benchmarks that illustrate that the performance of
geometric algebra can be close to traditional (linear-algebra-based) geometry
implementations, despite the much higher dimensionality of 2
n
for its internal
algebra. It describes techniques applied in
Gaigen 2, which is the efficient soft-
ware behind the GA sandbox source code package, and what we use in our
applications.
•
The Application Level (Chapter 23). You could consider the actual use of geometric
algebra in your own application the fourth implementation level. In Chapter 23 we
give an example of such practical use, in the form of the description of a ray tracer
that was implemented using the conformal model. We describe the equations of the
ray tracer in actual code and highlight decisions such as picking the right confor-
mal primitive to represent a particular concept. The benchmarks of Chapter 22 are
based on this ray tracer.
