Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

472 CONFORMAL OPERATORS CHAPTER 16

16.3.3 POSITIVELY SCALED RIGID BODY MOTIONS

The combination of a translation T, a rotation R, and a positive scaling S (all with arbitrary

center) can always be brought in the standard form TRS. This is most easily shown by

considering swapping the rotors pairwise, as follows:

•

The swapping law for translation and rotation is

R = RT

−1

t R

as we saw in (13.12).

•

Rotation and scaling in the origin commute,

I␾

= S

I␾

since their generating bivectors do.

•

Scaling and translation do not commute, but satisfy

= S

−γ

You can derive this algebraically or conﬁrm it by the simple sketch of Figure 16.4.

Because of these commutation properties, we can always convert any sequence of rotors S,

R, and T into the standard order TRS, with suitable adaptation of the rotor parameters.

These rotors generate a logarithmic spiral; in 3-D. This can be used to generate a snail shell

from a well-chosen circle, as in Figure 16.3. Note that this direct application to the 3-blade

Figure 16.3: A positively scaled rigid body motion rotor repeatedly applied to a circle and a

point (both displayed in light colors) generates an escargoid (snail shell).

SECTION 16.3 SCALING 473

−

x + t

x + e

−

× e

Figure 16.4: Swapping the order of a scaling rotor and a translation rotor implies that the

translation needs to be rescaled.

of the circle implicitly uses the structure preservation of the rotor, and is therefore typical

of the conformal model. In the ﬁgure, we have also applied the same rotor to a small

sphere to give a better impression of the 3-D nature of the shell.

16.3.4 LOGARITHM OF A SCALED RIGID BODY MOTION

Reﬁning the step size in the generation of transformations like Figure 16.3 should be done

through interpolation of the rotor, completely analogous to the interpolation of rigid

body motions in Section 13.6 and of rotations in Section 10.3.4. Correspondingly, we

need a logar ithm for this type of rotor to enable the computation of the required V

1/N

perform the rotor V in N steps, as exp



log(V )/N



To determine the logar ithm of the positively scaled rigid body motion V = TRS,we

collate some partial results ﬁrst.

•

We have already determined the logarithm of the rigid body motion part TR,in

(13.15).

•

Scaling and rotation commute, so the logarithm of a rotor of the form RSis easy to

determine:

log(R

I␾

) = log(R

I␾

) + log(S

) = −I ␾/2 + γ o ∧∞/2,

the sum of the logarithms of the commuting rotors.

474 CONFORMAL OPERATORS CHAPTER 16

•

The really new combination is that of a rotor of the type TS. This can be determined

to be

log(T

) = log(T

t γ/(e

−1)

) + log(S

) = −

− 1

t∞/2 + γo ∧∞/2, (16.4)

as you can verify by exponentiation and convenient grouping of terms into power

series. If γ = 0, the fractional coefﬁcient should take its limit value 1.

For the general positively scaled rigid body motion rotor in the form V = TRS,we

decompose the rotor into known elements by applying the earlier factorization in the

log for a rigid body motion of Section 12.5.3. We split off the part perpendicular to the

plane of R,towriteV = T

I␾

−v

) S

. The translation over w = (t ∧ I)/I is not

affected by the rotation and therefore interacts with the scaling as (16.4). The other part

should be descr ibed as the translation of a rotor of the type RS, so we need to look for its

center, as the location c satisfying

I␾

c − v] + v = c,

which solves to c = (1−R

)

−1

(1−R

) v = (1−R

)

−1

(tI)/I (where we used (13.13)).

Relative to this center, the motion V is in standardized form RS, and its logarithm can be

taken. That then needs to be translated to the correct in-plane location and composed

with the remaining w component. Combining all these ingredients produces the rather

intimidating

log(T

I␾

) =

1 − e

((t ∧ I)/I) ∞/2 + T

(1−e

)

−1

(tI)/I

[−I␾/2 + γ o ∧∞/2].

To apply this formula, you need to retrieve the parameters occurring in it from the total

rotor V. This is done by observing that −o(V∞) = −o(Re

γO/2

∞) = Re

γ/2

. Employing

the additional demand on the normalization of the rotor R



R = 1,weﬁndR and γ. Divid-

ing out these rotors from V gives the rotor T. The parameters of R and T are computed

as in Section 7.4.4. As we did there, if R = 1, you can set I = 1 and ␾ = 0.Ifγ = 0 (so

that S = 1), the fractional coefﬁcient of (t ∧ I)/I should take its limit value for small γ,

which is −1 (this is automatic if you rewrite it in terms of a sinch function). The resulting

function is indicated in Figure 16.5. The exceptions for R are similar to the earlier rigid

body motion logarithm of Figure 13.5.

Having the logarithm gives us the tool we need to interpolate these motions in the usual

manner, and it was used to generate the stepwise transformation of the elements in

Figure 16.3.

Theversorofanegatively scaled rigid body motion is not a rotor. It cannot be written

in exponential form and does not have a logarithm. Since you cannot do such a motion

piecewise anyway, you should not want to interpolate it.

SECTION 16.4 TRANSVERSIONS 475

log(V){

X = −o(V∞)

γ = log(X



if (γ == 0) then (no scaling)



= 1

else



= γ/(e

− 1)

endif

S = e

γo∧∞/2

R = Xe

−γ/2

T = V



t = −2 oT

if (R

== −1) return (“no unique logarithm”)

if (R

== 1) (no rotation, so no I)

log = −γ



t ∞/2 + γ o ∧∞/2

else

I = R

/R



␾ = −2 atan2(R

,R

)

= 1 − (1 − e

)

−1

(tI)/I ∞/2

log = −γ



(t ∧ I)/I ∞/2 + T

(−I␾/2 + γo ∧∞/2)



endif

}

Figure 16.5: Computation of the logarithm of a positively scaled rigid body motion rotor V.

One may improve subsequent numerics by making sure to return a bivector through taking

the grade-2 part log

16.4 TRANSVERSIONS

In the classical literature on conformal operations, one introduces the operation of

transversion. This may be deﬁned as the triple composition of an inversion in the unit

sphere, followed by a translation, followed by another inversion in the unit sphere. It is

easy to compute its rotor, which simpliﬁes nicely:

(o −∞/2) (1 − t∞/2)(o −∞/2) = 1 + o t = e

The two inversions make it a handedness-preserving operation, a proper conformal trans-

formation represented by an even versor, which is even a rotor. You might prefer to use

476 CONFORMAL OPERATORS CHAPTER 16

the analogy with the introduction of a Euclidean rotation as the reﬂection in two planes

with a common line, and deﬁne the transversion as the reﬂection in two spheres with a

common point (use structural exercise 5 to show that this is essentially the same as the

deﬁnition above).

From its form, the transversion clearly completes our types of primitive rotors in the con-

formal model using the last remaining factor of the bivector basis for its exponent (after

−t∧∞/2 for translations, γ o ∧∞/2 for scaling, and a Euclidean −I␾/2 for rotations). The

full list is in Table 16.1.

Table 16.1: Basic operations in the conformal model and their versors. The improper

transformations have vector versors, and change handedness. The reﬂection in the origin is

an even versor, but not a rotor, and it has no exponential form. The proper conformal trans-

formations are composed from even unit versors and can be written as the exponentials of

bivectors. The table shows that all elements in the bivector basis are associated with a speciﬁ-

cally named operation.

Type of Operation Explicit Form Exponential Form

reﬂection in origin plane n none

reﬂection in real unit sphere c −∞/2 none

reﬂection in origin o ∧∞ none

rotation over ␾ in I-plane cos(␾/2) − sin(␾/2) I e

−␾I/2

translation over t 1 − t∞/2 e

−t∧∞/2

scaling by e

cosh(γ/2) + sinh(γ/2) o ∧∞ e

γo∧∞/2

transversion over t 1 + o t e

o∧t

SECTION16.6 GENERAL CONFORMAL TRANSFORMATIONS 477

Table16.2: Common proper transformations of some of the standard elements of the conformal model. The entry marked

“Involved” is just the product of the transversions of ∞ and E.

Translation Rotation Scaling Transversion

Element e

−t∞/2

R e

γ o∧∞/2

ot/2

o t = o + t +

∞ o e

−γ

o o

∞ ∞ ∞ e

∞ t



≡∞+ 2t + 2t

E −(E∞)t RE



R E E + o(2tE)

E∞ E∞ (RE



R)∞ e

E∞ Inv olved

o ∧ E ∧∞ (o + t) ∧ E ∧∞ o ∧ (RE



R) ∧∞ o ∧ E ∧∞ o ∧ E ∧ (∞ + 2t)

o −∞/2 t −∞/2 o −∞/2 e

−γ

(o − e

2γ

∞/2) o − t



A closed-from solution to the logarithm of a general conformal transformation also

involving a transversion is not yet known.

16.5 TRANSFORMATIONS OF THE STANDARD BLADES

It is convenient to have a table with the most used transformations in standard form

applied to the elements in standard form. This is Table 16.2.

Contemplating this table, it is striking how the same versor operation leads to very differ-

ent explicit forms for the various elements. In actual computations, it is of course often

simpler to compute with the versors as long as possible, converting to explicit form only

at the end—if at all. This applies both to computations done by hand and by using a

computer. The use of versor products keeps the software clear and reduces errors. Only

in very time-critical applications would you write things out—and even then, geometr ic

algebra is useful since it provides the code generator with the automatically correct way

of transforming arbitrary elements.

16.6 GENERAL CONFORMAL TRANSFORMATIONS

With the reﬂections and the complete suite of rotors, we can make any conformal trans-

formation. The usefulness of these still needs to be explored, for although they are familiar

in mathematics, they are rather new to computer science. In the framework of geometric

algebra, they can of course be applied to any element, and that leads to interesting

operations.

478 CONFORMAL OPERATORS CHAPTER 16

(a) (b)

Figure 16.6: Loxodromes generated by applying the rotor exp



(o ∧ e

− e

∧∞)/10



multiple

times to a circle: (a) in the e

∧ e

-plane, (b) in 3-D space.

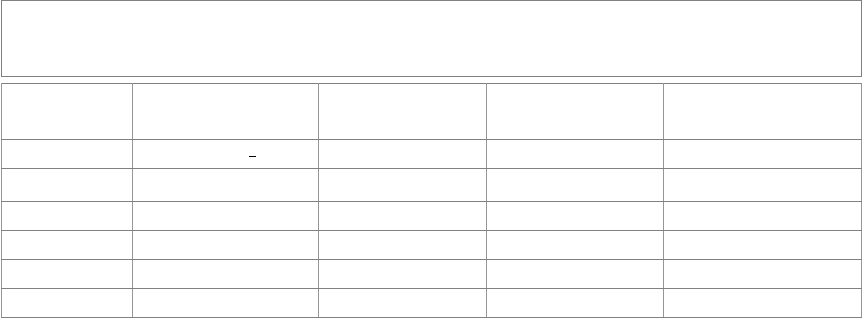
16.6.1 LOXODROMES

Figure 16.6(a) shows what we get when applying the rotor

L ≡ e

o∧e

−e

∧∞

(16.5)

to a circle multiple times. (We actually applied L

1/N

to show its action piecewise.) This

is a loxodromic transformation, known from the study of the conformal group in two

dimensions. As the ﬁgure suggests, it has two special points, a source and a sink, and it

scales, translates, and rotates elegantly between them.

The geometric algebra characterization of this transformation extends the classical treat-

ment in two ways: it makes the transformation easily applicable to arbitrary basic elements

such as ﬂats and rounds (and the circle example gives a lot more insight in the structure of

the mapping than merely transforming a point would have done). Also, there is no reason

to limit the space to two dimensions; the same rotor works to transform n-dimensional

space. The strange 3-D wormlike ﬁgures that result are best appreciated by an interactive

software package such as

GAViewer [18]; Figure 16.6(b) shows a rendering.

SECTION16.6 GENERAL CONFORMAL TRANSFORMATIONS 479

A rich class of shapes can be generated in this manner. Their simple expressibility means

that they are easily reﬁned, which is what one would wish from graphics primitives, so

they may be useful to solid modeling. But this remains to be explored.

16.6.2 CIRCULAR ROTATIONS

More immediately useful are circular rotations, which have rotation orbits not around

a line (as in Figure 15.5) but around a circle K. Such a circular rotation is of the form

exp(K

∗

). Each element p ∧ K

∗

= (pK)

∗

is a circle, curving around the circle K,asin

Figure 16.7. You can use this to your advantage to compactly generate a torus given its

two generator curves (a dual line and a dual circle). You may explore this in structur al

exercise 7, which generates the torus in Figure 16.12.

The mere fact that circles can be used as basic descriptors to rule objects can already save

a lot of memory and computation to manipulate them. This also remains to be explored.

16.6.3 M

OBIUS TRANSFORMATIONS

The usual way to study conformal transformations in mathematics is by means of M

obius

transformations, so we mention that brieﬂy. This technique, developed for 2-D, represents

a vector as a complex number z and a conformal transformation as the mapping

Figure 16.7: The circular orbits of a circle K, of the form p ∧ K

∗

480 CONFORMAL OPERATORS CHAPTER 16

z →

az+ b

cz+ d

By choosing the complex numbers a, b, c, and d appropriately, one can generate inversions,

translations, rotations, and the other conformal transformations.

Since ratios are important, it makes sense to introduce complex homogeneous coordi-

nates in the complex plane. Then the M

obius transformations admit a matrix representa-

tion: multiplication of the transformations is the same as multiplying the complex-valued

matrices





For instance, the conjugated inversion in the unit circle at the origin is represented by the

matrix





, and a translation over t by



1 t



(where t is the complex number corre-

sponding to t). Such representations allow one to compute products of conformal trans-

formations easily.

All this is very clever, but also very limited. The matrix description of conformal trans-

formations is very much point-based and, because of its use of complex numbers, tied to

2-D space. No such restr ictions are felt when treating conformal transformations using

the rotors of the conformal model. As we have seen before when discussing rotations and

quaternions, there is no need to go to complex numbers to get an algebra that properly

encodes the geometry.

16.7 NON-EUCLIDEAN GEOMETRIES

The conformal model can also be used for the description of other geometries. Hyperbolic

and elliptic geometry ﬁnd a natural home. We brieﬂy mention the connection; more may

be found in [15].

16.7.1 HYPERBOLIC GEOMETRY

In Euclidean geometry, we kept the null vector ∞ invariant, because we wanted it to

represent the point at inﬁnity. We can model hyperbolic geometry in the conformal

model by keeping the vector e = o −∞/2 invariant instead. This is the (dual) unit

sphere, and we obtain in this manner the Poincar

e disk model of hyperbolic geometry.

Or rather, a Poincar

e hyperball, for the conformal model is not limited to 2-D. By

letting the spherical border play the role of inﬁnity, the whole metric of the space must

adapt in precisely the right manner.

We brieﬂy indicate the parallel with Euclidean geometry, for convenience of terminology

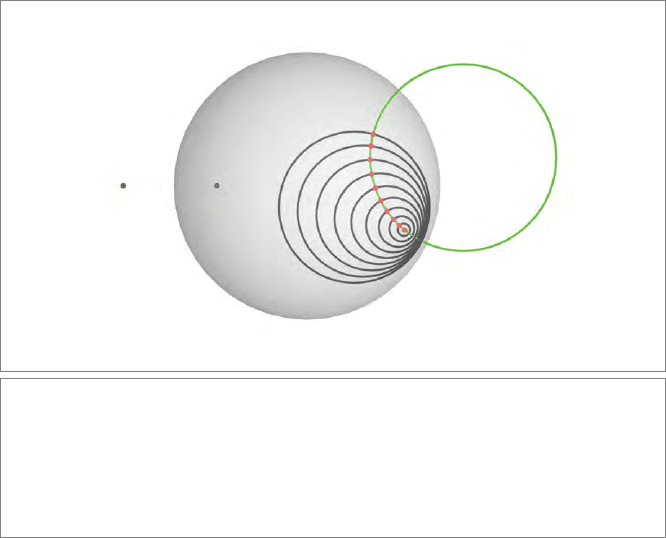
and depiction taking the 2-D case as in Figure 16.8. We are used to our lines of

in direct

representation to be represented as 3-blades with a factor ∞; in 2-D hyperbolic geometry,

SECTION16.7 NON-EUCLIDEAN GEOMETRIES 481

the corresponding special elements must contain a factor e.Asaconsequence,theydonot

plunge into the point at inﬁnity ∞, but into the unit sphere e. In the Poincar

e depiction,

they look like circles, as depicted in Figure 16.8.

Translations took place along Euclidean straight lines; in hyperbolic geometry, they

must go along the hyperbolic lines. The translation along the line L in Euclidean space

is by a rotor with exponent −∞L/2; in hyper bolic space, this becomes the rotor

exp(−eL/2) .

That has a strange consequence. Because of the null nature of the translation bivector

in the Euclidean case, distance was clearly additive in the usual Euclidean sense. In the

hyperbolic case, additivity of the translation bivector generates a metric that looks rather

distorted on the Poincar

e disk. In Figure 16.8 we have indicated circles with the same

center and increasing radii. Near the circle at inﬁnity e, distances apparently become very

large, and the points inside cannot escape the disk.

Hyper bolic motions can be made with versors that preserve e, and these can be generated

by vectors of the form n + δ

e. The conformal representation for this geometry can then

run completely parallel to how we handled Euclidean geometry in Chapter 13.

Figure 16.8: 2-D hyperbolic geometry in the conformal model. By considering the real dual

unit circle e = o −∞/2 as inﬁnity, the hyperbolic lines become circles in the plane that meet

the unit circle perpendicularly. (One such line is indicated as the green circle.) Translations

are deﬁned as moving elements along spherical lines. We show translated points at equal

increments of hyperbolic distance, and the corresponding hyperbolic circles. This gives an

impression of the hyperbolic metric on the Poincar

e disk. A ﬂat point in the hyperbolic plane

consists of a point and its (unreachable) reﬂected twin outside the disk, indicated in blue.