Дорожинський О.Л., Тукай Р. Фотограмметрія
Подождите немного. Документ загружается.

Професор І. Антіпов довів, що цього негативного явища можна позбутись,
якщо до рівнянь взаємного орієнтування додається умова рівності координат
зв'язкових точок.
2.7.5. Сумісне визначення елементів взаємного орієнтування та
передавання масштабу для двох суміжних моделей
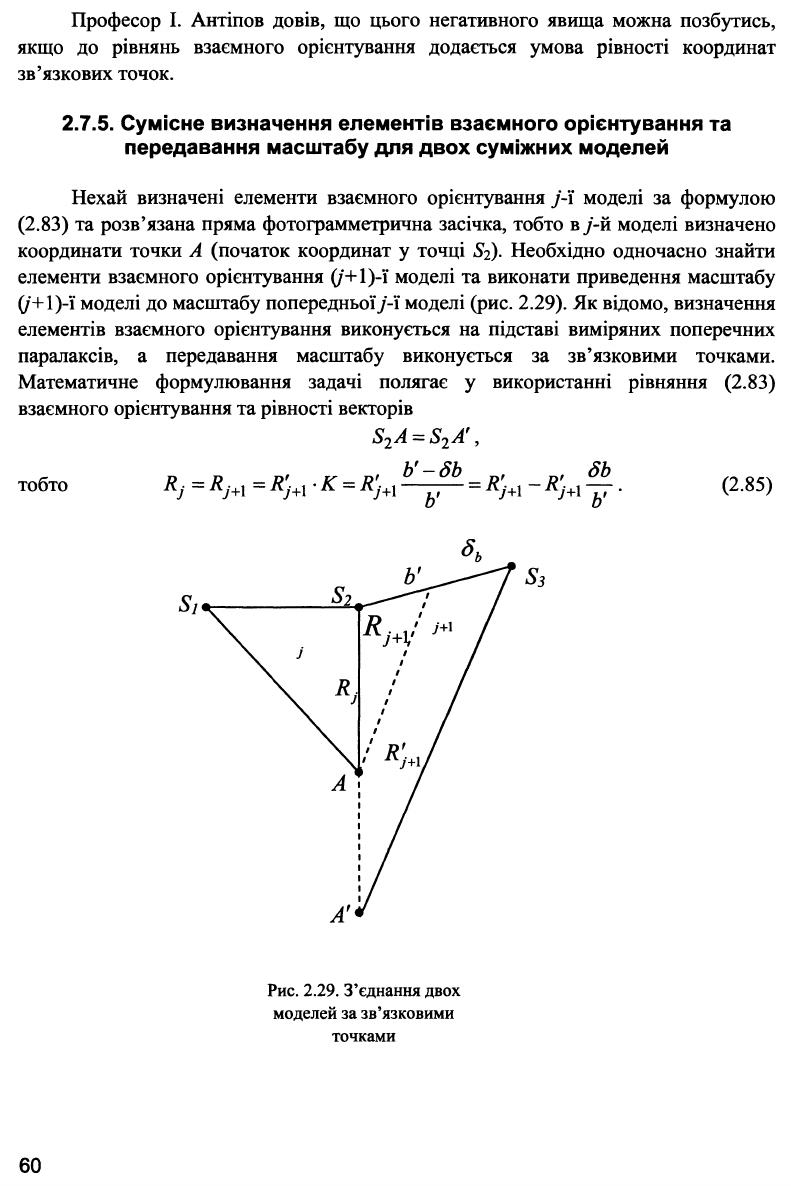
Нехай визначені елементи взаємного орієнтування j-ϊ моделі за формулою
(2.83) та розв'язана пряма фотограмметрична засічка, тобто
в у-й
моделі визначено
координати точки А (початок координат у точці S
2
). Необхідно одночасно знайти
елементи взаємного орієнтування (/+1)-ї моделі та виконати приведення масштабу
(/+1)-ї моделі до масштабу попередньоїу-ї моделі (рис. 2.29). Як відомо, визначення
елементів взаємного орієнтування виконується на підставі виміряних поперечних
паралаксів, а передавання масштабу виконується за зв'язковими точками.
Математичне формулювання задачі полягає у використанні рівняння (2.83)
взаємного орієнтування та рівності векторів
S
2
A
—
S
2
A!,
тобто
(2.85)
Si
А'
S
3
Рис. 2.29. З'єднання двох
моделей за зв'язковими
точками
60

Строго кажучи, рівняння (2.85) є нелінійним відносно шуканих елементів
г, ν, Δα, Δ БА, ΔΑ:, Δ6 І тому треба було б застосувати описаний вище прийом
лінеаризації (розклад функції у ряд Тейлора).
З практичного погляду, враховуючи, що \R\»|z| та те, що розв'язання задачі
відбувається ітеративно, перепишемо (2.85) так:
^Sb
+
Zj - Zj
+
i
=
v
b
, (2.86)
або a
b
-Sb + l
b
=Vb. (2.87)
Отже, для всіх точок (/+1)-ї стереопари складається система рівнянь (2.83), до
неї долучаються рівняння (2.87), записані для зв'язкових точок, і одночасно
розв'язується система нормальних рівнянь з 6 невідомими
Χ
=
[δτ δν δΑα δΑω δΑκ 0bf. (2.88)
У разі застосування МНК послідовність розв'язання така:
1. Для кожної зв'язкової точки розв'язують пряму фотограмметричну засічку
у 7-й моделі.
2. Задаються наближеними значеннями елементів взаємного орієнтування та
базису в (/+1)-й моделі ν°, Δα
0
, Αω°, Акb° .
3. Для кожної пари виміряних точок обчислюють коефіцієнти та вільні члени
(2.74), (2.75).
4. Для кожної зв'язкової точки розв'язують пряму фотограмметричну засічку
у (/+1)-й моделі, використовуючи спочатку наближені (а потім уточнені) параметри
(елементи взаємного орієнтування та базис).
5. Для кожної зв'язкової точки складають рівняння (2.87).
6. Складають нормальні рівняння, отримують розв'язок (2.88).
7. Обчислюють уточнені значення невідомих
Γ = + (<fr)
(0
,
V
= v° + (δν)Μ,
Δα = Δα
0
+ (<5Δα)
(,)
, Αω
=
Αω°
+
(δΑω)
(ί)
, (2.89)
ΔΑ:
= ΔΑ:
0
+ (δΑκ)
{ί
\ b
=
b° + .
8. Перевірка ітераційного процесу на збіжність аналогічна до (2.81), тільки
додається перевірка
9. Оцінка точності розв'язання задачі аналогічна до (2.82), тільки в
знаменнику стоятиме величина (п-6).
61

Зазначимо, що геометричну сутність рівнянь (2.85) вперше використав проф.
А. Скірідов, назвавши їх "умовою бокових сторін". Він також запропонував
використати цю умову для уточнення кутового орієнтування моделі на
універсальних стереоприладах.
Як вже зазначалось, проф. І. Антіпов застосував цю саму умову у побудові
мережі маршрутної фототріангуляції методом залежних моделей. Таке одночасне
розв'язання задачі визначення елементів взаємного орієнтування та передавання
масштабу принципово змінило проблему "невизначеності елементів взаємного
орієнтування". Оскільки детермінант сукупної системи нормальних рівнянь
відрізняється від нуля, то розв'язок задачі є завжди стабільним.
2.7.6. Геодезичне орієнтування фотограмметричної моделі
У результаті розв'язання прямої фотограмметричної засічки, описаного в
п. 2.7.1, отримують просторові координати точки А моделі об'єкта (рис. 2.25). Якщо
система SXYZ є абсолютною (геодезичною), і кути нахилу знімків та базису
визначені в цій системі, то зрозуміло, що модель будується в абсолютній системі
координат.
Проте найчастіше система SXYZ є відносною, і тому треба знайти елементи
геодезичного орієнтування моделі:
υ = [х
0ф
γ
0φ
Ζ
0φ
а
0
ω
0
к
0
t]
T
. (2.90)
З геометричного погляду ця задача складається з трьох дій (рис. 2.24):
- перенесення початку координат з центра О
Φ
у центр О;
- "поворот простору";
- зміна масштабу моделі, тобто приведення його до величини t.
Формули перетворення координат є такими:
Yr
=
+ A
Y
ζ
Оскільки функції (2.91) є нелінійними відносно вектора (2.90), то приведемо
їх до лінійного вигляду:
Я А + b
x
5Yo + с
х
&
0
+ d
x
Sa
0
+ β
χ
δω
0
+ f
x
Stc
0
+ g
x
St + /, = ν,,
a
y
SX
0
+ b
y
SY
0
+ c
y
5Z
0
+ d
y
Sa
0
+ e
y
Sa>
0
+ /
у
3к
0
+ g
y
8t + l
y
=v
y9
(2.92)
a
z
SX
Q
+ b
z
SY
0
+c
z
SZ
0
+ d
z
Sa
0
+ β
ζ
δω
0
+ /
ζ
δκ
0
+g
z
5t + l
z
= v
z
.
62

Тут:
а
х=1
ь
х
=0>
с
х=°>
а
у
= 0, Ь
у
=
1,
с
у
=0,
а
2
= 0, b
z
= 0, c
z
=l,
d
x
= -ΔΖ, = -Δ7sin a
0
, f
x
= (a
2
X -
a
x
Y)t,
=
AX,
d
y
=0, e
=
-AYtgco
0
—Ζ
· U
f
y
= Φ
2
Χ -
b,
Y)t, g
y
=
AY,
7
COS^o
d
z
=AX, e
z
=A7cosa
0
, /
z
=(c
2
X-q7V, g
z
=AZ,
AX
=
(a
x
X
+
a
2
Y
+
a
3
Z)t, l
x
=X
0
+AX-X
r
,
AY
=
(b
l
X
+
b
2
Y
+
b
3
Z)t, l
y
=Y
0
+AY-Y
r
,
AZ
=
(c
x
X
+
c
2
Y
+
c
z
Z)t, /
z
=Ζ
0
+ΔΖ-Ζ
Γ
.
У рівняння (2.92) входять сім невідомих. Для однозначного розв'язання задачі
треба мати дві планово-висотні опорні точки (вони дають шість рівнянь) та одну
висотну (дає одне рівняння). Тоді задача розв'яжеться без контролю.
Найчастіше беруть чотири планово-висотні точки, розташовані по кутах
стереопари, і розв'язують задачу, використовуючи МНК.
Знаходження вектора (2.90) є ітераційним і принципово не відрізняється від
описаного у п. 2.7.2 чи 2.7.4.
Метод придатний до застосування за будь-яких значень елементів
геодезичного (абсолютного) орієнтування моделі.
2.8. Геометричні перетворення, вживані у фотограмметри
У фотограмметрії доводиться оперувати такою математичною категорією, як
перетворення простору. Найуживанішим є проективне перетворення дво- або
тривимірного простору. Подамо в стислій формі найпоширеніші у фотограмметрії
типи перетворень.
1. Проективне; має вигляд:
у'
=
А
т
у, (2.93)
де А - матриця перетворень, (detv4*0); у - вектор початковий; у - вектор
перетворений.
2. Афінне; має вигляд:
х' = Ах + Ь, (2.94)
де А- матриця перетворення; х,х\Ь- вектори-стовпчики.
Ї
і
63

Властивості цього перетворення: площина, лінія і відрізок переходять
відповідно у площину, лінію і відрізок; не порушується паралельність прямих і
площин; зберігається метрика векторів; трикутник переходить в трикутник.
Особливий випадок цього типу перетворення:
x'
=
RAx
+
b, (2.95)
за умови, що
А~
1
=А
Т
,
тобто А - ортогональна матриця, а вектор R є діагональною матрицею, тобто
R =
Rn
R
22
(2.96)
R
mr?
3. Афінне у разі збігу осей координат; має вигляд:
χ*
=
Ах, (2.97)
дейсїА
4. Афінне зі збереженням подібності; має вигляд:
х' = кАх + Ь, (2.98)
д,ек>0,А~
1
=А
т
.
Властивості цього перетворення:
- кути зберігаються;
- зберігається подібність фігур;
- зберігається пропорційність відрізків;
- не порушується перпендикулярність векторів.
5. Афінне подібне середнє:
х'
=
кАх, (2.99)
тобто отримане з (2.98) за умови Ь=0. У цьому разі зберігається початок системи
координат.
6. Гомотетія:
x
f
=
Ax, (2.100)
тобто з (2.99) к=1.
7. Ізометрія:
х' = Ах + Ь. (2.101)
Тут зберігаються довжини векторів.
64

8. Ізометрія середня:
х' = Ах. (2.102)
Тут збігаються початки систем координат.
9. Поворот простору:
х'
=
Ах, (2.103)
де A~
l
=A
T
, det = 1.
10. Перенесення:
х' = х + Ь, (2.104)
А
=
Е,к
=
1.
Властивість: Змінюється початок системи координат.
11. Симетричне відображення:
= (2.105)
А-Е, к = 1, випливає з (2.99).
Властивість: Змінюється орієнтування у просторі.
12. Ідентичне перетворення:
X' =
JC,
(2.106)
тут зберігаються всі елементи.
Звернемо тепер увагу на деякі аспекти геометричних перетворень. Спочатку
розглянемо перетворення площини Ε у площину Ρ (рис. 2.30).
Для визначення положення точки а на площині Ρ прийнята довільна (не
прямокутна) система координат 0'х
х
х
2
. Для так званих невласних точок (перетин
двох паралельних прямих) ці координати не дають змогу визначити їхнє
розміщення. Тому у проективній геометрії положення точки визначається його
напрямком. Напрямок вектора визначається співвідношенням його складових к:т.
Для будь-якої точки а (рис. 2.30) визначальним є відношення:
Уі'У
2
-Уз=
х
і-
х
2
:1
- (2-107)
Έ
65

Координати y
l9
у
2
, у
3
називають однорідними координатами точки а у
системі О'Х\Х
2
·
Співвідношення (2.107) означає пропорційність складових к.
Для кожної точки площини можна записати
к
Уі
:к
у2
:к
у
^
=
х
х
:х
2
Л. (2.108)
Звідси можна зробити висновок, що системі однорідних координат у (л+1)-
вимірному просторі може відповідати довільна система координат и-вимірного
простору.
З (2.107) маємо:
jc
1
=A
5
jc
2
=^-. (2.109)
Уз Уз
Для тривимірного простору необхідно взяти чотири числа, тобто (2.107)
запишеться так:
Уі'>У2
:
Уз
:
У4=
х
і
:х
2
:х
з
:1
> (2.110)
к
у
х
'· ку
2
:
ку
3
:
ky
4
= х
\ '·
х
2
'·
х
з
:
1
·
Якщо врахувати (2.93) - лінійне перетворення, то для четвірки чисел
запишемо:
= а
\\
Х
1
+ а
\2
х
2
+ α
13*3
+
а
\4
х
4>
к
у
2
=
а
2\
х
\
+
α
22
χ
2 +
а
23*3
+
*24*4>
(2-111)
ку
3
=
ЛзЛ
+
а
32
х
2
+
а
33
х
3
+
а
34
х
4
,
к
ул
=
а
4х
х
х
+
а
42
х
2
+ а
43
л;
3
+
а^х
4
.
З (2.111) та (2.110) легко отримуємо формули для обчислення координат при
геометричних проективних перетвореннях.
Для тривимірного простору:
к
У\
=
а
\\
х
\
+ **12*2
+
+ ^14*4
к
у4
#41*1 + ^42^2 +
а
43
х
3
+ а
44
Х
4
к
У2
=
а
2\
х
\ +
д
22*2 +
а
23
х
3
+
а
24
х
4
ку
4
а
4\
х
\
+
а
42
х
2
+ а
43
х
3
+ а
44
х
4
к
УЗ
=
а
3\
х
\
+
а
32
х
2
+ **33*3 + **34*4
ку
4
а
4\
х
\
+ а
42
х
2
+ а
43
х
3
+ а
44
х
4
Ставиться вимога, щоб для матриці перетворень det
А
* 0.
(2.112)
66

Рівняння (2.112) можна спростити, розділивши чисельник і знаменник у
(2.112) на 044*4.
Ввівши позначення для величин
α44 Л44 Х
4
Q44
χ
4
-Μ-
=
Α
η
ζ іт.д., (2.113)
отримаємо:
^A
xx
x
+
A
l2
y
+
A
x3
z
+
A
i4
Уі
A
4X
x
+
A
42
y
+
A
43
z
+
l
у =
AllX + Лг2У + + Аі4
, (2.114)
А
41
х + А
42
у + Α
43
Ζ +1
_А
зх
х
+
А
32
у
+
Α
33
ζ
+
А
34
у
3
—
.
А
41
х + А
42
у + Α
43
Ζ +1
Для двовимірного простору (перетворення площини на площину) маємо
у
3
= 0, ζ = 0 і відповідно
А
хх
х
+
А
х2
у
+
А
хз
·
А
4Х
х + А
42
у +1
у2==
А
21
х
+
А
22
у
+
А
2 3 (2п5)
А
4Х
х
+
А
42
у
+
\
Для одновимірного простору (перетворення прямої на пряму) відповідно
запишемо:
(2Л16)
А
2Х
Х
+
1
Серед описаних вище перетворень назвемо декілька найвживаніщих.
Перетворення тривимірного простору на тривимірний (3D * 3D) у випадку
евклідового простору (прямокутної системи координат). У цьому разі матриця А з
(2.103) є ортогональною, а величини у
4
та х
4
з (2.112) відсутні. Тоді (2.103)
запишеться так:
у
х
=а
хх
х
х
+а
Х2
х
2
+a
X3
x
3
,
Уг =
а
2\
х
\
+
а
22
х
2
+ ^23*3 >
(
2 л 17
)
у
3
=а
31
х
х
+а
32
х
2
+а
33
х
3
.
67

Матриця
а
и
°12
а
п
А =
а
21
а
22 °23
_°31 °32
а
33
(2.118)
є матрицею напрямних косинусів і описує поворот однієї системи координат
відносно іншої.
Про цю матрицю ми вже подали відомості у π. 2.3.2. За формулами (2.7)
обчислюють компоненти матриці напрямних косинусів, а позначення літерами
може бути таке, як в (2.8) або в (2.118).
Перетворення тривимірного простору на двовимірний (3D * 2D) (англ.
Direct Linear
Transformation —
DLT).
Тоді уз з (2.114) відсутнє і маємо
Уі =
_А
п
Х + A
n
Y + A
l3
Z + A
l4
А
41
Х
+
A
42
yY
+
A
43
Z +1
_ А
2
\Х + a
22
Y + A
23
Z + А
2
4
" А
41
Х
+
А
42
у Υ
+
Α
43
ζΖ +1
Це перетворення з 11 невідомими параметрами.
(2.119)
Перетворення площини на площину (2D * 2D) як афінне перетворення зі
збереженням подібності (2.98).
Тоді маємо, якщо к=1
у
{
=
а
п
Х
+
a
l2
Y
+
l\
у
2
=
a
2l
X
+
α
22
Υ
+ Ь
2
.
(2.120)
—і τ
Оскільки А =А , то матриця А є матрицею напрямних косинусів і є
функцією тільки одного кута κ повороту системи координат. У такому разі
а
п
= а
2
2, а
2
\ = -а
і2
і бачимо, що це є перетворенням з чотирма невідомими
параметрами.
Перетворення площини на площину (2D *2D) з незбіжністю масштабів за
осями
координат.
Це перетворення описується рівняннями (2.95) - (2.96). Тоді
y^R^X
+
a^
+ by
y
2
=R
2
(a
2l
X
+
a
22
Y)
+
b
2
або ж, якщо
R\=R
2
=l
у
х
-а
п
Х
+
a
X2
Y
+
Уг =a
2l
X
+
a
22
Y
+
b
2
і це є перетворення з шістьма параметрами.
(2.121)
68

Перетворення Гельмерта описується рівняннями
0 1 2
(2.122)
у
=
Ь
0
+ а
2
Х
+ α{Υ
і є чотирипараметричним двовимірним перетворенням, виконує зміну масштабу,
"поворот простору (площини)" та паралельне перенесення.
Нелінійні перетворення у двовимірному просторі (зокрема такі, що
використовуються у цифровій фотограмметрії при допасуванні оптичних
щільностей для пікселів -
див.
т. зв. операція Resampling).
Одним з них є білінійне перетворення типу
х
=
аь+ОуХ
+
a
2
Y
+
α
3
ΧΥ,
і
y
=
b
0
+b
l
X
+
b
2
Y
+
b
3
XY.
Це перетворення з 8 невідомими параметрами.
Інші типи нелінійних перетворень (кубічна інтерполяція, поліном Лагранжа,
сплайн-інтерполяція) подано у п. 4.6.
2.9. Математичні моделі похибок фотограмметричних вимірів.
Вплив кривини Землі
2.9.1. Моделі похибок фотограмметричних вимірів
Фотограмметричні вимірювання супроводжуються значним впливом різних
за своєю природою чинників, які викликають похибки у вимірах. У загальному
вигляді виділимо такі основні групи чинників:
1) що спричиняють відхилення реальної моделі центральної проекції від
ідеальної;
2) що супроводжують вимірювання фотокоординат;
3) нестрогого математичного оброблення (використання нестрогих
функціональних залежностей, апріорні допущення про ймовірну природу
похибок).
Всі ці похибки доволі добре вписуються у гіпотезу адитивної структури
похибок, запропоновану Ю.В. Кемніцом [8] (адитивна - дослівно "отримана
підсумовуванням"):
£ = Θ + Δ, (2.124)
де Є- повна, Θ - систематична, Δ - випадкова похибки.
Кожна з вищеназваних трьох груп наявна як у векторі похибок©, так і у
векторі похибок Δ.
Проаналізуємо кожну з цих груп окремо.
69
