Дорожинський О.Л., Тукай Р. Фотограмметрія
Подождите немного. Документ загружается.


Класичним прийомом розв'язання задачі є приведення нелінійних
залежностей до лінійного виду розкладанням у ряд Тейлора, обмежуючись
частинними похідними першого порядку.
Перепишемо (2.25) у вигляді:
F
x
=x
=
~f
a
{
{X-X
s
)
+
b
x
(Y-Y
s
)
+
c
x
(.Z-Z
s
)
a
3
(X-X
s
)
+
b
3
(Y-Y
s
)
+
c
3
(Z-Z
s
)
F
a
2
(X-X
s
)
+
b
2
(Y-Y
s
)
+
c
2
(Z-Z
s
)
' ^
J
a
3
(X-X
s
)
+
b
3
(Y-Y
s
)
+
c
3
(Z-Z
s
)
Розкладання в ряд Тейлора дає:
(2.48)
F
y -
F
0y +
dF
x
dX
s
dX
s
+
dF
x
dY
s
dY
s
dF
x
+——
Ms
dZ
s
dF
x
+ —-
da
. dF
x
dF
x
da
+
—-dm
+
—-άκ
dm дк
dF
y
dX
s
•dX
s
dF
y
+ —-
dY
s
•dY
s
dFy
+ —-
•dZ
s
dFy
+ —-
da
dF dF
v
-da
+
——άω
+
—
L·
dκ
dm дк
(2.49)
Переходячи від нескінченно малих приростів dXs до кінцевих SX
s
..., позначаючи частинні похідні
dF
x
dX*
—
а
х
вільні члени F
0x
=
l
x
, F
0y
=
l
y
та
допускаючи, що виміряні величини х, у супроводжуються похибками, з рівнянь
(2.49) отримаємо рівняння поправок:
Тут
a
x
SX
s
+
b
x
SY
s
+
c
x
SZ
s
+
d
x
Sa
+
β
χ
δω
+
/
χ
δκ
+
Ι
χ
=ν
χ
>
a
y
SX
s
+
b
y
SY
s
+
c
y
SZ
s
+
d
y
5a
+
e
y
Sco
+
/
у
3к
+
I
y
= v
y
°
x+
°
y = +
b
r
+
b
3
x\ b
y
=
\-(b
2
f
+
l^y),
R
1
> R
1
(2.50)
c
*
+Cy =
Έ^
+
d
x
=£[c
l
(X-X
s
)-a
l
(Z-Z
s
)]
+
±[c
3
(X-X
s
)-a
3
(Z-Z
s
)],
Κ κ
e = -/ sin
K
+
X
tgd)
+
Y-Ys"
Rcosco;
(2.51)
fx
= У>
f
v
=
-x,
50

d
y
=£[c
2
(X-X
s
)-a
2
(Z-Z
s
)]
+
^[c
3
(X-X
s
)-a
3
(Z-Z
s
)],
e =-f
COSK
+у
tgco +
Y-Y
s
^
R coso);
l
x
=F
0x
l
y =
F
0y
R
=
a
3
(X-X
s
)
+
b
3
(Y-Y
s
)
+
c
3
(Z-Z
s
).
Як відомо з математики, застосування (2.49) дає змогу отримати остаточний
розв'язок за допомогою послідовних наближень (ітерацій). Рівняння (2.50) записані
для однієї точки; якщо ж таких точок декілька, то (2.50) запишеться у вигляді
системи рівнянь поправок (у матричному представленні)
AX
+
L
=
V.
(2.52)
Тепер до системи (2.52) можна застосувати метод найменших квадратів
(МНК).
У такому разі (застосування МНК) послідовність розв'язання задачі така.
1. Задаються наближеними значеннями елементів зовнішнього орієнтування:
у0
ν
0
Ύ
0 0 Jb
*s
9
^s9 α
9
ω
9
κ .
(2.53).
2. Для кожної опорної точки (їхня кількість дорівнює ή) обчислюють
коефіцієнти
а
Х9
Ь
х
та вільні члени І
х
, І
у
. У результаті цих дій формується матриця
коефіцієнтів
А =
2 и,6
а
і
л
х
\
л
ч
л
°Уп Κ
л
л
/д
1
Λ
Λι
/д
/»
(2.54)
та матриця вільних членів
А=['
ч
'л U ·
2и,1
Уп •
3. Складають систему нормальних рівнянь
A
T
AX
+
A
T
L
=
0
(2.55)
та знаходять розв язок
51

де
X
=
-(A
T
Ay
l
A
T
L,
Χ
=
[δΧ
5
SY
s
SZ
s
δα δω δκ]
Τ
4. Обчислюють уточнені значення шуканих невідомих
κ
=
κ°+δκ
(ί)
+·
Тут індекс (і) означає номер наближення (ітерації).
5. Перевіряють ітераційний процес на збіжність:
\δχ¥-δΧ^\<ε
Χ3
,
\δΥ<^-δ^\<ε
Υ5
,
\δα^-δα^\<ε
α
,
\δω
(ί)
-δω
(Μ)
\<ε
ω
,
(2.56)
(2.57)
(2.58)
(2.59)
де ε - задані допуски.
Якщо всі умови (2.59) задовольняються, то процес наближень вважається
завершеним
і
за остаточне значення вектора невідомих приймають величини (2.58).
У протилежному випадку переходять до пункту 2.
6. Оцінюють точність отриманого розв'язку так. Обчислюють середню
квадратичну похибку одиниці ваги:
Σ(
ν
χ
+ν
ν)
1
/(2и-6),
(2.60)
де
v
X9
v
y
знаходять за (2.50), підставляючи в ці рівняння знайдені остаточно значення
невідомих.
52

У пункті 3 з розв'язку системи нормальних рівнянь одержана обернена
матриця
Q
=
(A
T
A)~
l
. (2.61)
Діагональні коефіцієнти матриці Q дають змогу обчислити середні
квадратичні похибки елементів зовнішнього орієнтування:
m
Xs
=
М>І0п>
rn
Y
s=MyiQ
2
2>
(262)
т
а = М^ОМ*
т
со = Му/ОН*
т
к = W&6'
Викладений метод придатний для знімків з довільними елементами
орієнтування. Для отримання стійкого розв'язку необхідно виконати дві такі
головні умови:
- опорних точок необхідно мати не менше від трьох і вони не повинні
розташовуватись на одній прямій;
- наближені значення елементів зовнішнього орієнтування повинні бути
відомі з певною точністю, інакше розв'язання буде тривати або дуже довго, або
ітераційний процес взагалі стане неможливим; на практиці для лінійних елементів
зовнішнього орієнтування Xs, Ys наближені значення можна визначити за картою
або сумістити з координатами однієї з опорних точок, a Z^ =
Z
7
+ /
· m
(де Z, -
висота будь-якої опорної точки; т - знаменник масштабу знімка; / - фокусна
віддаль знімка); якщо виконувалось планове аерофотознімання, то наближені
значення кутів нахилу знімка приймають такими, що дорівнюють нулю.
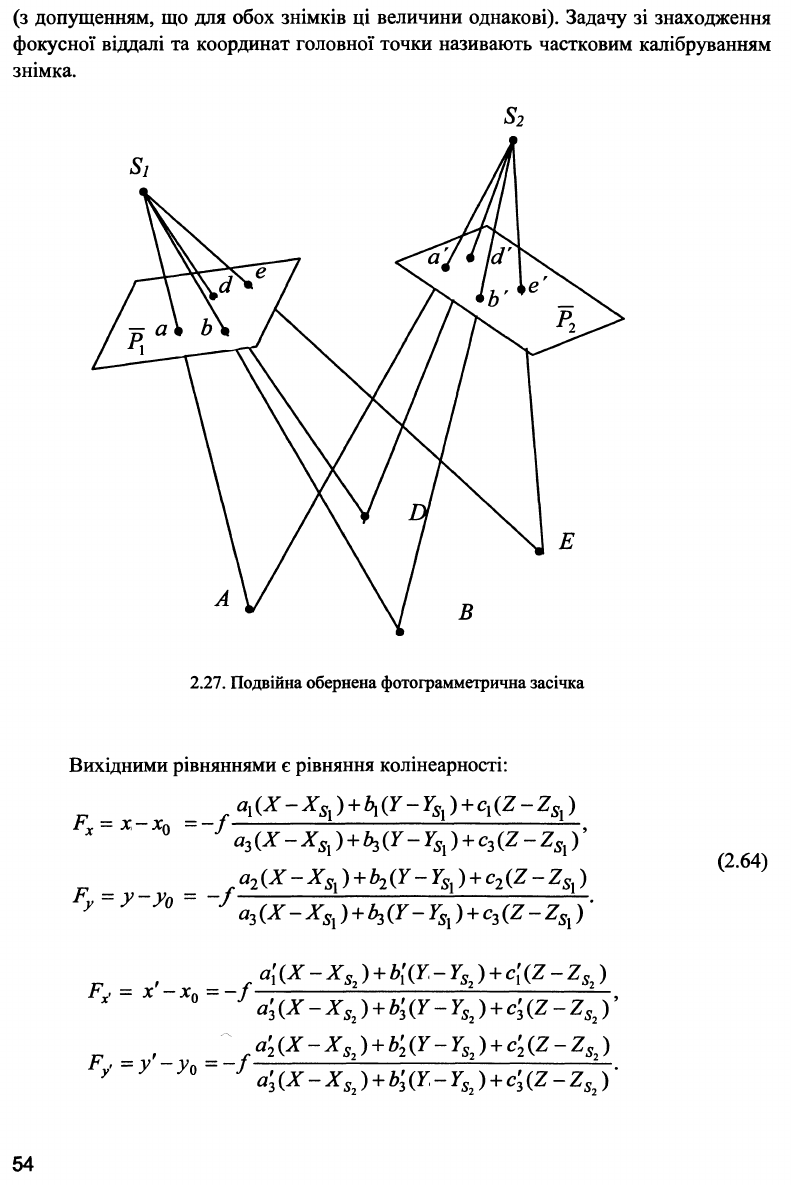
2.7.3. Подвійна обернена фотограмметрична засічка
Ця задача відрізняється від попередньої тим, що тут беруть участь два знімки
Р
х
і Р
2
(рис. 2.27).
Нехай на місцевості задано опорні точки А, В, D, Ε з відомими
координатами Х
9
Υ, Ζ. На знімках Р
х
і Р
2
ці точки зобразились в a,a\b
9
b\ ;
для них виміряні координати х
9
у, х, у'. Теоретично допустимо, що деяка опорна
точка зобразилась тільки на одному зі знімків.
Необхідно знайти елементи зовнішнього орієнтування для обох знімків та
елементи внутрішнього орієнтування, тобто вектор невідомих такий:
X
=
[
X
S
X
Y
S
X
Z
S
X
<*\
X
S
2
Y
S
2
Z
S
2
a
2
ω
2 *2 *0 Уо fj·
(2.63)
Як бачимо, задача порівняно з π. 2.7.2 поширена на два знімки. Окрім цього,
вектор (2.63) розширений на знаходження елементів внутрішнього орієнтування
53
(з допущенням, що для обох знімків ці величини однакові). Задачу зі знаходження
фокусної віддалі та координат головної точки називають частковим калібруванням
знімка.
&
Вихідними рівняннями є рівняння колінеарності:
х Х Х
° •
/
a
3
(X-X
5l
) + 03(7-7
5l
) + c
3
(Z-Z
Sl
)'
У
У Уо J
а
3
(Х-X
S{
)
+
b
3
(Y-Y
Si
)
+
с
3
(Ζ-Z
Sl
)'
F = χ'-χ f
a
'
,(X+ b[{Y+ C
'
(Z
">
' * a',(X-X
s
J
+
b',(Y-Y
S2
)
+
c^Z-Z
SI
Y
, a'
2
(X-X
S2
)
+
b'
2
(Y-Y
S2
)
+
c'
2
(Z-Z
S2
)
F
,
= ν
— Vn
=
—
f = —.
' a'
3
(X-X
S2
)
+
bUY-Y
S2
)
+
c'
3
(Z-Z
S2
)
54

Рівняння поправок порівняно з (2.50) є розширеними:
a
x
Sx
s
x
+b
x
5Y
s
x
+c
x
Sz
s
x
+d
x
Sa
x
+е
х
5щ +/
χ
δκ
λ
+g
x
Sf
+
h
x
Sx
0
+s
x
Sy
Q
+l
x
=v
x
,
a
y
SX
S{
+b
y
5Y
Sy
+c
y
SZ
Sx
+d
y
Sa
l
+e
y
So)
l
+/
у
6к
х
+
g
y
Sf
+
h
y
Sx
Q
+s
y
Sy
Q
+l
y
=v
y
,
(2.65)
djx
h
+СҐМ +
g
'
x
<r+a>
0
+s>
0
+/; =v;,
dJSC^ +b'
y
SY
Si
+J
y
8Z
Si
+d'
y
Sa
1
+f
y
SK
2
+g'
y
$-+h'
y
3c
0
+s'
y
fy
0
+l'
y
=v'
y
;
тут всі вирази є такими самими, як і в (2.51), а для частинних похідних при
δf, δχ
0
, Sy
0
маємо:
g
x
h
x
=h'
x
=l,s
x
=s'
x
=l, (2.66)
g
y
=^,h
y
=h'
y
=l,s
y
=s'
y
=l.
Структура рівнянь графічно виглядає так:
X
S\
Y
S\
Z
S\ αι ύ>ι κι Xs
2
Y
s
2
Z
S
2
α
2
tih κ
2
f х
0
У о Ixy V
xy
Точ
ка а
точ
ка
а'
точ
ка Ь
точ
ка
У
Подальше розв'язання принципово збігається з описаним в п. 2.7.2.
Відмінність полягає лише в порядку системи нормальних рівнянь: якщо в
попередній задачі кількість невідомих дорівнювала 6, то тут маємо 15 невідомих.
Тому (2.59) розширяються до 15 перевірок. Для формул оцінки точності маємо
замість (2.60) і (2.62) такі:
μ
2
=jl(
v
*
2
+ vj +vj)j/(*-15), (2.67)
де η - загальна кількість рівнянь поправок (2.65);
55

m
Xs,
=
UyfQu >
m
Ys,
m
Zs
t
т
щ
=
VyjQss »
66'
m
Xs
2
™Ys
2
m
Zs
2
=
ΜΛΙΩ99 >
"«ι
=
M-^Qmo >
m
r
2
=
/*TJQ\212
'
m
f
=
MTJQUII »
=
МУ1<2Ш4,
т
Уо
=
M^Q1515 »
Формально мінімальна кількість опорних точок повинна становити чотири, і
вони повинні зобразитись на двох знімках. Тоді кількість рівнянь «=16. Ці точки не
повинні розміщатись на одній прямій.
Введення в задачу невідомих елементів внутрішнього орієнтування дещо
впливає на стабільність розв'язку. Для усунення цього недоліку необхідно, щоб
перепад висот між опорними точками був значним. У разі рівнинної місцевості
система рівнянь є погано зумовленою, і, як наслідок, точність визначення елементів
внутрішнього орієнтування є низькою.
2.7.4. Розв'язання задачі взаємного орієнтування
Рис. 2.28. Компланарність
векторів для роз'язання задачі взаємного
орієнтування
Нехай дана пара аерофотознімків,
отримана з базису фотографування SjjS
n
(рис. 2.28). Необхідно знайти елементи
взаємного орієнтування у
базисній
системі
а
л
, а
п
, к
л
, к
п
, ω
η
. В основу
розв'язання покладемо умову ком-
планарносіі. На підставі рівняння
скалярно-векторного
добутку
запишемо:
B-(R
X
XR
2
) = 0 .
(2.69)
Спроектувавши ці вектори на
осі координат, рівняння (2.43) подамо
у вигляді детермінанта (враховуючи,
що В
Х
=В, В =Β
Ζ
= 0):
В
0 0
γ;
Ά
X
2
η
3
= 0, (2.70)
або після розкладання по першому рядку маємо:
Β\Υ[Ζ
2
0
56

F = γ;ζ'
2
-
Y{Z[
= Ο. (2.71)
r r
Компоненти векторів R
x
та R
2
є функціями координат точок а
л
та а
п
знімків
та елементів взаємного орієнтування і описуються рівняннями (2.16).
Використовуючи ці формули для лівого знімка, треба враховувати, що ω
Λ
=0.
Рівняння (2.71) є нелінійним стосовно величин а
л
, л:
л
, а
п
, ω
η
, к
п
.
Використаємо прийом лінеаризації розкладанням (2.71) в ряд Тейлора:
г г0
dF . dF . dF . dF .
F
=
F" + da
n
+ άκ
Λ
+ da
n
+ dco
n
+ άκ
η
. (2.72)
да
л
дк
л
да
п
дсо
п
дк
п
З (2.72) одержимо рівняння поправок:
αδα
Λ
+
Ь8к
л
+
с8а
п
+
άδω
η
+
βδκ
η
+1 = ν, (2.73)
a
=
-X{Yi, b
=
Z'
2
B-Y{C, c
=
Υ{Χ
2
,
d
= Υ{Ε'
- Z[F\ e
= Y{C'
- Z{B'
E'
=
Y
2
cosa'
n
, C
=
c
2
x
x
-c
x
y
x
, B
=
b
2
x
l
-b
l
y
l
, f (2.74)
C
=
c
2
x
2
-c'y
2
, B'
=
b
2
x
2
-b[y
2
,
F' = x
2
b
3
sinκ'
η
-y
2
bcosK
r
n
+
/cos^,
/
=
Y{Z
2
-Z[Y
2
. (2.75)
Якщо в рівнянні (2.75) зробити певні спрощення за умови, що елементи
взаємного орієнтування - малі величини, то отримаємо:
І
= Я =
У\-Уі> (2.76)
де q - поперечний паралакс.
Нагадаємо про геометричний зміст задачі. Для визначення елементів
взаємного орієнтування необхідно на стереопарі виміряти поперечні паралакси q не
менше ніж в п'яти точках (парах точок), які розташовані у стандартних (або
близьких до стандартних) зонах стереопари. Для підвищення точності розв'язання
задачі вимірювання виконують при кількості точок більше ніж п'ять. Тому рівняння
поправок (2.73) утворять систему, аналогічну до (2.52).
У разі застосування МНК послідовність розв'язання задачі така.
1. Задаються наближеними значеннями елементів зовнішнього орієнтування
Λ:
0
а
0
ω° к°
Л
'
>
и
п '
ш
п
>
·
57

2. Для кожної пари виміряних точок (їхня кількість дорівнює п) обчислюють
коефіцієнти (2.74) та вільні члени (2.75). У результаті цих дій формується
матриця коефіцієнтів
А =
Я,5
а
\ Ь\
с
\
d
\
а
2
С
2
d
2
а
п Κ
с
п
d
n
е
п.
та матриця вільних членів
L=[l
x
/,
/7,1
u
(2.80)
3. Складають систему нормальних рівнянь
A
T
AX
+
A
T
L
=
0
та знаходять розв'язок
Χ
=
[δα„ δκ
Λ
δα„ δω
η
δκ
η
]
τ
.
4. Обчислюють уточнені значення шуканих невідомих
α
η
=αΙ+δαψ, α„=α°
η+
δα^,
κ
Λ
=κ«+δκ«\ κ
η
=κ°
η+
δ4\
ω
η
=ωΙ
+
δω^\
і - номер ітерації.
5. Перевіряють ітераційний процес на збіжність:
\δα?-δα^\<ε
α
,
\δα?-δα^\<ε
α
,
\δω?-δω^\<ε
ω
,
\δκ"-δκ™\<ε
κ
,
де ε - задані допуски.
У разі виконання всіх умов (2.81) ітераційний процес завершено. Якщо хоча б
одна з умов (2.81) не задовольняється, то переходять до пункту 2.
(2.81)
58

6. Після закінчення ітераційного процесу проводять оцінку точності. Середня
квадратична похибка одиниці ваги дорівнює
μ
2
=
2У
V і У
/("-5),
(2.82)
а середні квадратичні похибки елементів взаємного орієнтування обчислюють за
формулами аналогічними до (2.68).
У разі використання лінійно-кутової системи визначуваними елементами
взаємного орієнтування є величини г, ν, Δα, Αω, А/с (рис. 2.22). Відмінність від
попередньо розглянутого полягає в тому, що замість рівняння поправок (2.73) та
коефіцієнтів (2.74) маємо відповідно:
а -δτ
+
b δν
+
οδΑα
+
άδΑω
+
β SA/c
+
l
=
v, (2.83)
а
=
-{x\Z'
2
+
fX
2
)
sec2 τ
- (
χ
ι
γ
2 ~ У\
х
2
s
i
n
τ/cos
2
r,
b = (x{Y{ " У\Х2)
sec2 v
t
cos
r
>
С
= (У\-х№)Х'г +(ytgr
+
>'
1
tgi//cosr)Z2,
d
=
-{Jig τ + y
x
tg ν / cos г)[я
3
(X
2
sin ΔΑ: + y
2
cos ΔΑ:) - / sin ΔΑ sin ΔΦ] +
+(/ +
x
\
TG
v/cos г)[із (x
2
sin
ΔΑ:
+
Y
2
cos ΔΑ:) + / cos ΔΦ] + (2.84)
+(>>! -JC
1
TGR)[C3(X
2
SINAIR + ^2 COSAA:) + /cosAasinAtfj],
e
=
(figT
+
y
l
tgv/cosr)(a
l
y
2
-a
2
x
2
)-(f
+
x
x
tgv
!
cosT)(l\y
2
-b
2
x
2
)-
-(У\-*№)(С\У2-
с
2
х
2)·
Послідовність розв'язання задачі така сама, як і для елементів взаємного
орієнтування в базисній системі.
Аналіз розв'язання задачі показує, що точність взаємного орієнтування
залежить прямо пропорційно від фокусної віддалі знімків - для короткофокусних
аерофотокамер точність є кращою. Кути а
л
со
п
визначаються точніше порівняно
з кутами к
Л) п
; для лінійно-кутової системи елементи ν, Δα, Αω визначаються
краще ніж кутиг, ΔΑ:.
Задача взаємного орієнтування розв'язується погано або зовсім не
розв'язується, якщо сфотографована поверхня близька до поверхні циліндра, твірна
якого паралельна до базису фотографування. Це так звайа "умова невизначеності
взаємного орієнтування". Тоді детермінант матриці нормальних рівнянь є або
нулем, або близький до нуля.
59
