Должанський І.З., Загорна Т.О. Бізнесплан: технологія розробки

Подождите немного. Документ загружается.

Модуль 2. Зміст основних розділів бізнес%плану

нв

— витрати на освоєння нових виробів;

— сума цехових витрат;

— сума загальновиробничих витрат.

Основні виробничі фонди.

Коефіцієнт придатності основних фондів обчислюється за фор"

мулою:

= (С

— СЗ) : С

, (2.18)

де С

— первісна (балансова) вартість основних виробничих фондів;

СЗ — сума зносу основних виробничих фондів за весь період

експлуатації.

Загальну норму амортизації основних виробничих фондів розра"

ховують за формулою:

А = (С

+ В

кр

+ В

— С

) : С

Т, (2.19)

де В

кр

— витрати на капітальний ремонт;

— витрати на амортизацію основних виробничих фондів;

— витрати, пов’язані з ліквідацією основних виробничих

фондів;

Т — амортизаційний період років.

Фондовіддача — випуск продукції на 1 грн. (1000 грн.) вартості

виробничих фондів визначається відношенням обсягу випущеної

(товарної, валової, реалізаційної) продукції за певний період до за"

гальної (сумарної) середньорічної вартості усіх виробничих основ"

них і оборотних фондів.

Повна фондоємність продукції визначається відношенням серед"

ньорічної вартості основних виробничих фондів і оборотних коштів

до обсягу випущеної товарної (валової, реалізаційної) продукції за

певний період.

Виробнича потужність — максимально можливий річний обсяг

випуску продукції [5].

Коефіцієнт використання виробничої потужності визначається за

формулою:

= П

ср

*К

осв

: 100, (2.20)

де П

ср

— середньорічна виробнича потужність, що вводиться до дії

в поточному році;

Частина I. Теоретичні аспекти розробки бізнес%плану

осв

— коефіцієнт освоєння потужності, яка буде вводиться у по"

точному році.

Виробнича потужність цеху (ділянки), оснащеного однотипним

устаткуванням, визначається шляхом множенням нормативної річної

продуктивності однієї машини (агрегату) — П

, з урахуванням се"

реднього коефіцієнта перевиконання норм К

п/н

на число машин (аг"

регатів) — n:

= П

*К

п/н

*n. (2.21)

Виробнича потужність цеху (ділянки), оснащеного різним устат"

куванням, визначається продуктивністю парку ведучих груп устат"

кування. До ведучих груп належить устаткування, що виконує ос"

новний обсяг роботи (за складністю, трудомісткістю) з виробництва

основної (профільної) продукції.

Оборотні кошти.

Середня тривалість обігу оборотних коштів (оборотність у днях)

за рік, квартал визначається відношенням добутку середнього залиш"

ку оборотних коштів — О

сер

і кількості днів у періоді — Д до суми

реалізації — В

за цей період, тобто:

N = (О

сер

Д) : В

, (2.22)

або

N = О

сер

: (Вр : Д). (2.23)

При визначенні показників оборотності коштів кількість днів у

періоді приймається рівною за: рік — 360, півріччя — 180, місяць —

30. Оборотність може визначатися як у цілому для всіх оборотних

коштів, так і для окремо для нормованих і ненормованих.

Число оборотів оборотних коштів — n, коефіцієнт оборотності виз"

начається відношенням суми реалізованої за даний період продукції —

до середнього залишку оборотних коштів у цьому ж періоді:

сер

: n = В

: О

ср

. (2.24)

Цей показник так само характеризує розмір реалізованої про"

дукції, що приходиться на 1 (1000) грн. оборотних коштів.

Оборотні фонди.

Норма виробничих запасів матеріалів (загальна) визначається в

натуральному і грошовому вираженні:

Модуль 2. Зміст основних розділів бізнес%плану

Нзп = З

+ З

, (2.25)

де З

і З

— норма наявного і відповідно підготовчого запасу мате"

ріалу

— страховий (гарантійний ) запас матеріалу.

Норма незавершеного виробництва:

нв

= Т

нв

, (2.26)

де Т

— тривалість виробничого циклу, днів;

нв

— коефіцієнт наростання витрат.

Середньодобова потреба підприємства в матеріальних ресурсах

розраховується за формулою:

= М / Д

, (2.27)

де М — потреба в даному виді ресурсу на планований період (рік,

квартал) у натуральному вираженні;

— число календарних днів у періоді [25].

Прибуток і рентабельність.

Прибуток від реалізації продукції основної діяльності визначаєть"

ся за формулою:

= В + В

з.т.п.

+ В*

з.т.п.

— С

, (2.28)

де В — річний обсяг товарної продукції;

з.т.п.

і В*

з.т.п.

— вартість залишків товарної продукції відповідно

на кінець базисний і планований роки;

— собівартість реалізованої продукції.

Рентабельність виробу визначається відношенням прибутку, одер"

жуваного від цього виробу — П

— до повної собівартості його — С

—

і виражається у відсотках:

R = П

/С

100. (2.29)

Загальна рентабельність виробництва — R

заг

— визначається ча"

сткою від ділення суми загального балансового прибутку від промис"

лової діяльності — П — на повну середньорічну вартість основних

виробничих фондів Ф

осн

і нормованих оборотних коштів — Ф

об

— і

виражається у відсотках.

Рентабельність — показник ефективності виробництва, який ха"

рактеризує співвідношення між кінцевими результатами виробничо"

Частина I. Теоретичні аспекти розробки бізнес%плану

господарської діяльності і витратами на виробництво продукції. У

практиці планової роботи розраховується загальна рентабельність

виробництва і рентабельність продукції. [25] Перша обчислюється

як відношення балансового прибутку до середньорічної вартості ос"

новних виробничих фондів і нормованих оборотних коштів, тобто:

об

= 100П

: (Ф

осн

+ Ф

об

), (2.30)

де П

— балансовий прибуток;

осн

і Ф

об

— середньорічна вартість відповідно основних вироб"

ничих фондів і нормованих оборотних коштів.

Рентабельність окремих видів продукції розраховується як відно"

шення прибутку, отриманого від реалізації даного виду продукції —

— до собівартості — С, тобто:

= П

/ С

100. (2.31)

Цей показник характеризується ефективністю використання по"

точних витрат на виробництво і використовується для порівняння

результатів і витрат за конкретними видами продукції. Розрахунко"

ва рентабельність визначається як відношення балансового прибут"

ку (за винятком плати за фонди, трудові та природні ресурси, пла"

тежів за банківський кредит) до середньорічної вартості основних

виробничих фондів і нормованих оборотних коштів. Рентабельність

виробництва значною мірою залежить від ефективності просування

товару до споживача.

Цей процес у маркетингу одержав назву «просування товару» або

«рух товарів». Воно здійснюється двома основними способами: са"

мостійно або з використанням послуг посередників.

Для одержання вихідної інформації, за допомогою якої розроб"

ляються показники, необхідно застосовувати різні джерела і методи

одержання інформації.

Розрахунок беззбитковості та графік беззбитковості.

Розрахунок ведеться на підставі прибутків і витрат і рівня ціни

на одиницю продукції. Ціль розрахунку — визначення критичного

обсягу виробництва і запасу «Фінансової міцності» підприємства.

Критичний обсяг виробництва (V

кр

) визначається за формулою:

кр

= УПВ/(Ц — УППВ), (2.32)

де УПВ — сума умовно"постійних витрат, грн;

Модуль 2. Зміст основних розділів бізнес%плану

Ц — ціна одиниці продукції, грн;

УППВ — сума умовно"перемінних витрат на одиницю продукції, грн.

«Запас фінансової міцності» визначається як різниця між плано"

ваним розміром виторгу і розміром граничного виторгу і відображає

розмір, до якого можна знижувати обсяг виробництва або ціну про"

дукції для того, щоб виробництво не виявилося збитковим.

«Зіставленням критичного обсягу виробництва з планованим

випуском продукції визначається дата, з якої проект почне приноси"

ти прибуток. Для побудови графіка беззбитковості варто скласти

рівняння наступного виду:

= ах,

= а

+ а

х, (2.33)

де у

— виторг, грн;

— витрати (повна собівартість) на виробництво продукції, грн;

а — ціна одиниці продукції без ПДВ, грн/од.;

х — планований обсяг реалізації продукції, од.;

— сума умовно"постійних витрат (УПВ), грн;

— сума умовно"перемінних витрат на одиницю продукції

(УППВ), грн/од.» (3).

Обґрунтування фінансово"економічної доцільності реалізації пла"

нованого виробництва можна дати на основі приведених нижче по"

казників, за якими визначається ліквідність, платоспроможність,

фінансова незалежність, стійкість і стабільність підприємства, а го"

ловне — очікуваний строк окупності проекту (табл. 2.19).

Розрахунок коефіцієнтів здійснюється за даними прогнозного

балансу активів і пасивів підприємства, за даними розділу «План

виробництва» бізнес"плану.

Коефіцієнт абсолютної ліквідності (К

а.л

) розраховується за фор"

мулою:

а.л

= Кошти/Короткострокові пасиви. (2.34)

Рекомендоване значення К

а.л.

= 0,2.

Коефіцієнт швидкої ліквідності (К

) розраховується за формулою:

ш.л.

= (Кошти + Дебіторська заборгованість) / Короткострокові

пасиви (2.35)

Критичне значення К

ш.л

= 1.

Частина I. Теоретичні аспекти розробки бізнес%плану

Коефіцієнт покриття балансу (К

п.б

) розраховується за формулою

ДО

п.б

= Оборотні активи / Короткострокові пасиви. (2.36)

Рекомендоване значення К

п.б

= 2.

Загальний коефіцієнт автономії (К

об

) розраховується за формулою:

об

= Капітал і резерви / Баланс. (2.37)

Рекомендоване значення К

об

> 0,6.

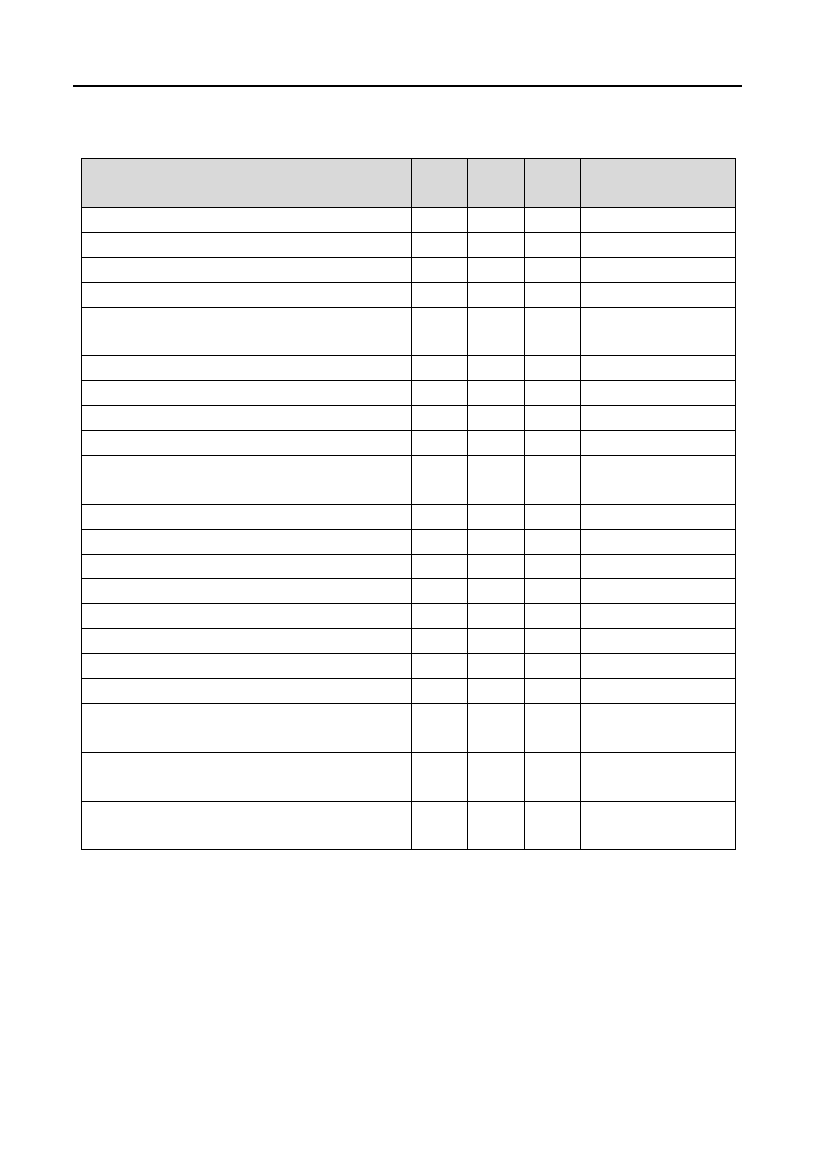
Таблиця 2.19

Фінансово%економічні результати діяльності підприємства

Коефіцієнт 1й

рік

2й

рік

3й

рік

Середній показ

ник по галузі

Коефіцієнти ліквідності

– коефіцієнт швидкої ліквідності 1,0

– коефіцієнт абсолютної ліквідності 0,2

– коефіцієнт покриття балансу 2,0

Коефіцієнти фінансової незалеж"

ності і стійкості

– загальний (коефіцієнт автономії) > 0,6

У частині формування запасів > 0,7

– коефіцієнт фінансової стійкості 1,25

Коефіцієнти ділової активності

Тривалість оборотності, днів Кращий по

галузі

а) запасів

б) дебіторської заборгованості

в) кредиторської заборгованості

г) операційного циклу (а + б)

д) фінансового циклу (г – в)

Фондовіддача основних коштів, грн

Коефіцієнти прибутку

– рентабельність продажів, %

– рентабельність основної діяль"

ності, %

– рентабельність авансованого ка"

піталу, %

Термін окупності проекту, років Нормативний

термін окупності

Модуль 2. Зміст основних розділів бізнес%плану

У частині формування запасів (К

зап

) розраховується за фор"

мулою:

зап

= (Капітал і резерви + Довгострокові пасиви — Позаоборотні

активи) / Запаси. (2.38)

Рекомендоване значення К

зап

>0,7.

Коефіцієнт фінансової стійкості (К

ст

) розраховується за фор"

мулою:

ст

= Капітал і резерви/(Довгострокові пасиви + Короткостро#

кові пасиви). (2.39)

Рекомендоване значення К

ст

> 1,5.

Тривалість обороту запасів (Д

об.с

) у днях розраховується за фор"

мулою:

об.с

=З*360/N, (2.40)

де З — середньорічна вартість оборотних коштів,

N — виторг від реалізації продукції.

Тривалість обороту дебіторської заборгованості (Д

д.з

) у днях роз"

раховується за формулою:

д.з

= ДЗ*360/N, (2.41)

де ДЗ — середньорічний розмір кредиторської заборгованості.

Тривалість обороту кредиторської заборгованості (Д

к.з

) у днях

розраховується за формулою:

к.з

=КЗ*360/S, (2.42)

де КЗ — середньорічний розмір кредиторської заборгованості;

S — повна собівартість.

Фондовіддача основних коштів (Ф

) розраховується за форму"

лою:

= N/ОФ, (2.43)

де ОФ — середньорічна вартість основних фондів.

Рентабельність продажів (R

) розраховується за формулою:

= П/N*100%, (2.44)

де П — балансовий прибуток.

Частина I. Теоретичні аспекти розробки бізнес%плану

Види ризиків Негативний вплив на прибуток

Нестійкість попиту Падіння попиту із зростанням цін

Поява альтернативного продукт

Зниження попиту

Зниження цін конкурентів Зниження цін

Збільшення виробництва в

конкурентів

Падіння продажів або знижен"

ня цін

Збільшення податків Зменшення чистого прибутку

Зниження платоспроможності

споживачів

Падіння продажів

Зростання цін на сировину, ма"

теріали, перевезення

Зниження прибутку через зро"

стання цін на сировину, мате"

ріали, перевезення

Залежність від постачальників,

відсутність альтернативи

Зниження прибутку через зро"

стання цін

Нестача оборотних коштів Збільшення кредитів або зни"

ження обсягу виробництва

Рентабельність продукції (R

пр

) розраховується за формулою:

пр

= (П/S)*100%, (2.45)

де S — повна собівартість і реалізація продукції.

Рентабельність авансованого капіталу (R

а.к.

) розраховується за

формулою:

ак

= (П /АК) *100%. (2.46)

Термін окупності проекту (Т) розраховується за формулою:

Т = (Статутний капітал — Довгостроковий кредит) / П. (2.47)

Якщо планується здійснення проекту за рахунок кредиту, то

нормативний термін окупності проекту дорівнює термінові, на який

визначається кредит.

2.8 Аналіз ризиків реалізації бізнесплану

Значення розділу полягає в оцінці небезпеки того, що цілі, по"

ставлені в плані, не можуть бути досягнуті цілком або частково.

Складається перелік простих ризиків, з яких обираються най"

більш важливі для даного проекту. Особливої уваги приділяється

фінансово"економічним ризикам.

Модуль 2. Зміст основних розділів бізнес%плану

Ризик через утрату прибутку (падіння рентабельності) у резуль"

таті нестійкості попиту (положення на новому ринку) на плановану

продукцію може бути розрахований з використанням статистичних

методів.

Сутність статистичного методу оцінки ступеня ризику ґрунтується

на теорії імовірності розподілу випадкових величин. Це положення

означає, що, маючи достатню кількість інформації про реалізацію

певних видів ризику в минулих періодах для конкретних видів

підприємницької діяльності, будь"який суб’єкт господарювання здат"

ний оцінити імовірність реалізації їх у майбутньому. Дана ймовірність

і буде ступенем ризику.

Статистичний метод з визначення ризику проекту використовуєть"

ся для обчислення очікуваної тривалості кожної роботи і проекту в

цілому. Суть цього методу полягає в тому, що для розрахунку ймовір"

ностей виникнення втрат аналізуються всі статистичні дані, що стосу"

ються результативності здійснення розглянутих операцій. Частота ви"

никнення деякого рівня втрат визначається за наступною формулою:

обш

(2.48)

де f — частота виникнення деякого рівня втрат;

К — число випадків настання певного рівня втрат;

заг

— загальне число випадків у статистичній вибірці.

Для побудови кривої ризику і визначення рівня втрат уводиться

таке поняття як область ризику.

Для розрахунку ступеня певного виду ризику необхідно знати

закон його розподілу, тобто володіти інформацією про те: при наяв"

ності яких умов він може бути реалізований; як його реалізація буде

відбита на діяльності господарського суб’єкта.

Математичне чекання даного відбивання являє собою суму до"

бутків усіх можливих значень на імовірність їхнього виникнення:

М(Х) = Х

+ Х

+...+ Х

, (2.49)

де М(Х) — математичне чекання;

, Х

— значення, що може приймати досліджуваний пара"

метр залежно від конкретних умов;

, Р

— імовірність прийняття цих значень.

100

Частина I. Теоретичні аспекти розробки бізнес%плану

Таким чином, імовірнісний зміст математичного чекання конк"

ретного параметра від проведення підприємницької діяльності поля"

гає в тому, що воно приблизно дорівнює середньому арифметично"

му його спостережуваних (можливих) значень.

Однак математичне чекання ще не є повною характеристикою

випадкової величини. Для більш повної її характеристики необхідно

використовувати й інші числові характеристики. Так, для того, щоб

оцінити, яким чином будуть розсіяні значення обраного параметра

(наприклад, прибутку) від його середнього прогнозованого значення

(тобто від математичного чекання) доцільно використовувати таку

характеристику, як дисперсія. Теорія ймовірностей визначає диспер"

сію як математичне чекання квадрата відхилення

(())

()

XMX n

−

∑

. (2.50)

Величина, за допомогою якої можна оцінювати розсіювання

(відхилення) можливих значень випадкової величини від її середнь"

ого значення, називається середньоквадратичним відхиленням. Се"

редньоквадратичне відхилення являє собою квадратний корінь з

дисперсії.

Середнє очікуване значення відхилення прибутку від його серед"

ньоочікуваного значення (середньоквадратичне відхилення) s роз"

раховується за формулою:

(())

МХ n

−

∑

(2.51)

де X — величина прибутку в кожному окремому випадку;

п — загальне число випадків.

Таким чином, економічний зміст середньоквадратичного відхи"

лення з погляду теорії ризиків полягає в тому, що воно є характери"

стикою конкретного ризику, що показує максимально можливе ко"

ливання певного параметру від його середньоочікуваного значення.

Дане положення дозволяє використовувати середньоквадратичне

відхилення як показник ступеня ризику з погляду імовірності його

реалізації. Причому, чим більша величина середньоквадратичного

відхилення, тим ризикованіше дане управлінське рішення і, відпо"

відно, більш ризикований даний шлях розвитку підприємства.