Doktorov E.V., Leble S.B. A Dressing Method in Mathematical Physics

Подождите немного. Документ загружается.

3.4 Elementary and tw ofol d Darboux transformations. General case 79

and the remaining ones are subsequently found:

−1

=(λ − μ)

−1

=(λ −μ)

−1

= ξ

−1

. (3.48)

Now the twofold transformations and the respective DT theorem can be

written and formulated. We introduce the twofold transformation as a se-

quence of two elementary ones in conjugate spaces. The ﬁrst one is made by

the inverse operator to E with the spectral parameter μ and the relevant so-

lution ϕ of the direct problem. The second map is generated by the r esultin g

function χ

expressed in the same way but from a linearly independent seed

solution χ of the equation (3.44) with the parameter ν. Another po ssibili ty

exists for the opposite order of actions. The formulation of the results is given

by Theorem 3.15:

Theorem 3.15. If the scalar product

(ζ,ϕ)

= pζϕp ∈ A

(3.49)

and c

∗i

are invertible in the subalgebra A

,andP is deﬁned by

P = ϕ(χ, ϕ)

−1

χ, (3.50)

then the twofold DTs for solutions of the direct ZS problem and for the con-

jugate one (3.29) with D

∗

= −D are given by the following equalities:



p +



−1

∗i





ψ +

ν − μ

λ − ν

Pψ



(3.51)

= ζ

(κp + σ

(

ζ −

ν − μ

κ − μ

ζP

)



p +



−1

∗i



. (3.52)

The p otentials a re given by



p +



−1

∗i



(u +(ν − μ)[J, P ])



p +



−1

∗i



. (3.53)

Note that the operator P is a projector.

The proof of covariance of the ZS equations can be performed by substitu-

tion of σ

from formulas for the conjugate problem analogous to (3.46) with

u → u

and φ → χ

. The structure of the twofold DT (3.51)–(3.53) in the

Abelian case and for c

= p

resembles the known results [354]. This means

that the iterated bDTs give a solution of the Riemann–Hilbert problem with

zeros. The iterations are generated by combinations of (3.51) and (3.52). By

the direct computation, the product of them provides

(ζ

,ψ

)=pζ

p =(ζ,ψ)+

(ν − μ)(κ − λ)

(κ − μ)(λ − ν)

ζφ(χφ)

−1

χψ . (3.54)

This formula fac il i tates the iteration process.

80 3 From elementary to twofold elementary Darboux transformation

One of the main purposes for the introduction of the twofold DT directly

is concerned with the problem of reductions [331]. The properties of the ZS

problem a nd its conjugate allow us to establish a class of reductions solving the

simple conditions for the eDT parameters that enter the binary combination

[280, 278, 281, 433] or go to the Lie algebra level [181, 361]. Combinations of

the twofold DTs were used to obtain multisolitons and other solutions of the

three-level Maxwell–Blo ch equations [449]. A straightforward generalization

can be obtained by replacing matrix elements by appropriate matrices. The

most promising applications of the technique are relat ed to operator rings.

Such an example was developed in [265].

3.5 Schlesinger transformation as a special case

of elementary Darboux transformation. Chains

and closures

We begin with recalling the deﬁnition of the eDT and its combinations. The

form we choose [265] combines results of the n ×n matrix representation with

a somewhat abstract extension of it based on the existence of idempotents and

the respective division r ing (skew ﬁeld) B in the associative diﬀerential ring

A over the ﬁeld K.LetD be a diﬀerentiation map on A and two idempotents

(projectors) p, q = e−p, e =id∈ A be ﬁxed by p = p

, pq = 0. The projectors

are rather general and all we should know about them is that both do not

depend on the parameters o f the theory and commute with D.

Consider the ZS problem L

ψ =(D+λJ −u)ψ =0, where λ ∈ K,u, ψ ∈ A,

connected with the element J = a

p + a

q, a

−a

= a = 0. The general eDT

ψ → ψ[1] = Eψ =(λp −σ)ψ is deﬁned by the element σ ∈ A via intertwining

relation EL

= L

u[1]

E. Analyzing the operator equations that follow from the

intertwining relation, one arrives at the important consequence qσq = c.It

can be shown that within this choice of the eDT (another eDT appears if one

interchanges p → q in the deﬁnition of the operator E) the element qσq = c

commutes with D; therefore, c is a constant. Denote

puq = u

= v

,qup= u

= w

. (3.55)

Here the index n marks the iteration number. We will consider equations

(3.55) as determining the chain equations. This chain is inﬁnite; therefore,

the choice of origin (n = 0) is arbitrary. Suppose there is a solution of the ZS

problem φ ∈ A

= pAp ⊕qAp, pφ= φ

∈ B, that corresponds to the spectral

parameter μ; suppose next that ∃φ

−1

and the gauge c = qeq are adopted.

The transforms

n+1

= acξ

+ μ

+ v

− Dv

n+1

= aξ

, (3.56)

and the additional “Miura” equation

Dξ

= −ξ

− μ

aξ

+ w

(3.57)

3.5 Schlesinger transformation. Chains and closures. 81

form a closed set of connections deﬁning the chain. It is enough to substi-

tute the eDT connections (3.56) into the Miura links (3.57) and express the

potentials v

via ξ. We obtain the potentials

= aξ

−1

n−1

−1

− aξ

−1

− ξ

−1

(Dξ

)ξ

−1

= aξ

n−1

, (3.58)

which yield the chain equation

aξ

−1

n+1

−1

n+1

− aξ

−1

n+1

− ξ

−1

n+1

(Dξ

n+1

)ξ

−1

n+1

= acξ

+ μ

[aξ

−1

n−1

−1

− aξ

−1

− ξ

−1

(Dξ

)ξ

−1

]

+[aξ

−1

n−1

−1

− aξ

−1

− ξ

−1

(Dξ

)ξ

−1

]ξ

× [aξ

−1

n−1

−1

− aξ

−1

− ξ

−1

(Dξ

)ξ

−1

]

− D[aξ

−1

n−1

−1

− aξ

−1

− ξ

−1

(Dξ

)ξ

−1

] . (3.59)

Remark 3.16. A straightforwa rd consequence of (3.58) and (3.59) leads to

a deﬁnite li nk between elements of the potential u. The link permits only

such constraints that are compatible with the deﬁnitions of ξ and φ.The

use of the second eDT (p ↔ q) immediately allows us to put constraints

with the whole powerful set of algebraic to ols [181] based on automorphisms

of the underlying Lie algebra [331] with grading [361]. It is obvious that

the scope of the whole theory is much broader than what we can present

here.

The Schlesinger transformation for nonzero elements of the potential is

deﬁned by the limiting case qσq = 0; this condition is degenerate for the

initial system of intertwining relations. Therefore one should solve the seed

equations from the very beginning [278, 289]. The advantage of employing the

Schlesinger transformation consists in the fact that in this case there is no

need to use the solu t ion of the auxiliary ZS problem, since the transformed

potential u

is expressed via the seed potential u only. Finally, the elements

of u are transformed by the Schlesinger transformation as

=(D

− Du

−1

− u

)(ac

)

−1

= −ac

−1

(3.60)

Suppose the inverse element u

−1

exists. The 2×2 matrix ZS problem enters the

KdV and nonlinear Schr¨odinger (NLS) theories together with the appropriate

choice of the second (covariant) Lax operator. As an illustratio n d enote u

v, u

= w.Afterthenth iteration we arrive at the chain system

n+1

=[v

′′

+(v

′

)

− v

]/ac

n+1

= ac

−1

. (3.61)

Reductions for the KdV and NLS theories are given by w

=1andv

= w

respectively. The simplest heredity condition v

n+1

= w

n+1

closes the chain

for the NLS case:

′′

− (v

′

)

/v = v

− ac

/v .

82 3 From elementary to twofold elementary Darboux transformation

This equation is integrated by the substitution v

′

= F (v). In terms of s = F

we have

/2 − s = v

− a

Integrating, we arrive at

′

+ a

+ c

where c

and c

are constants. The resulting diﬀerential equation is integrated

in elliptic functions. The study of a compatible Lax pair, e.g., for the NLS

equation, demands a “time” variable, additional to x. Let the “time” depen-

dence be deﬁned via the second Lax equation of the same (ZS) form as the

spectral equation. Then one arrives at the t-chain equation of the form (3.61)

but with diﬀerent constants. Combining both chains gives equations of a hy-

drodynamic type.

In the richer case of three projectors p, q,ands, we redeﬁne J as J = a

q + a

s. General equations for the eDT with the same form of intertwining

relations lead again to the constant elements qσq = c, sσs = d. In the generic

case of nonzero c and d the eDT transforms are determined in [269].

Consider now the Schlesinger transformations with restrictions to the po-

tential given by σ

= c =0, but σ

= 0. The covariance theorem has the

following formulation:

Theorem 3.17. Let σ

=0and assume u

−1

and σ

−1

exist and the condition

[c, σ

]=0holds. Then the equations for σ can be solved directly and the

transform of the potential of the ZS oper ator L

u → u

is determined by

=(Du

/a + σ

− u

/b)c

−1

= −abcu

−1

/(a − b) ,u

= −bσ

= −[(bσ

−u

−bDu

/a)u

−1

/a+u

/b−Dσ

]/σ

=(1− a/b)σ

−1

=[(1− a/b)σ

+ cu

−1

where

=(Du

+ u

−1

/b , σ

= bcu

−1

/(a − b) ,

and σ

is found fr om the equation

−1

Dσ

= −





−1

1 −

−1

In general, where there are more than two projectors, we have the additional

possibility of nonzero σ

The chain equations with the new possibilities to further construct solu-

tions may be derived by the algorithm that is described at the beginning of

this section and leads to the analog of (3.59). The simplest applications con-

cern 3 × 3 matrix problems with known reductions to N -wave, KdV–MKdV,

Hirota–Satsuma, and Oikawa–Yajima equations [211, 269, 278, 458].

3.6 Twofold Darboux transformation and Bianchi–Lie formula 83

3.6 Twofold Darboux transformation

and Bianchi–Lie formula

We have introduced the twofold transformation as a sequence of two elemen-

tary ones in conjugate spaces. The ﬁrst transformation is performed by the

inverse operator to E with the spectral parameter μ and the corresponding

solution of the direct problem ϕ. The second map is generated by the resulting

functions χ

= E

−1

χ expressed in the same way but from a linearly indepen-

dent seed solution χ of the conjugate ZS equation with the parameter ν.The

ﬁnal form of the transformation is written as [269]

= ψ + βϕ

(

χ, ϕ)

−1

χψ , β =

ν − μ

λ − ν

. (3.62)

The analog of a scalar product is introduced by

(χ, ϕ)

= pχϕp ∈ A

= pAp

and the inverse exists in A

. It is easy to check that the transform of the

potential may be rewritten in terms of the idempotent P = φ(χ, ϕ)

−1

χ as

= U +(ν − μ)[J, P ] ,

for example,

= u

+ aϕ

(χ, ϕ)

−1

(ν − μ) .

Remember that J = a

p + a

q, a

− a

= a = 0. An analog of the position

vector at the ring under consideration can be deﬁned as before. Let us denote

γ(λ)=(λ −μ)(λ −ν)

−1

and s = ψ

−1

Pψ. Then the solutions obtained by the

twofold transformations (3.62) yield

= r +

∂γ(λ)

∂λ

−1

The element s is determined by the seed solution only. This formula generalizes

the Bianchi–Lie transformation for the non-Abelian entries. The existence of

the inverse element ψ

−1

is supposed and the identity (1 + βP)

−1

=1− βP/

(β + 1) is taken into account.

As for the complete set of projectors, the form



ABp

=(A, B)=

(B,A) is symmetric; therefore, it may be regarded as an analog of the Killing–

Cartan metrics. The length of the vector s is then unity. The transform may

be generalized further for the case of the iterated twofold DTs as

r[n]=r +



i,λ

s[i]/γ

We conclude with the remark that dealing with a few projectors [269] may

produce various versions of the Schlesinger transformation whose non-Abelian

version seems interesting from the point of view of quantum problems.

84 3 From elementary to twofold elementary Darboux transformation

3.7 N -wave equations: example

The general dressing by the DT allows us to solve non-Abelian three-wave

systems when a linear term is added. Among these systems there is the matrix

equation that goes after reduction to the classical N-wave systems with linear

terms. The linear terms can account for such an important phenomenon as

asynchronism. In this case the so-called inclined solitons occur, with a loss o f

symmetry between the leading and back wavefronts [269, 272], see the next

subsection for pictures. The classical (Abelian) three-wave system is discussed

in Sect. 8.5.

3.7.1 Twofold DT of N -wave equations with linear term

Let us consider the set of n idempotents p

. The elements a

∈ K deﬁne

combinations

M =



,N=



If elements of the ring are functions of parameters t and y, for arbitrary Ψ ∈ A

the internal derivative ad

Ψ =[x, Ψ] may deﬁne the ﬁrst-order problem v ia

the combined diﬀerential op erators D

t,y

. The general idea of the twofold DT

as a symmetry of a nonlinear system is demonstrated by two linea r equations

called the Lax pair (3.63) for an auxiliary matrix function Φ(t, y),

Φ = −λMΦ +



H, M



Φ, (3.63)

Φ = −λNΦ +



H, N



Φ,

with the following deﬁnitions of matrices (n = 3):

M =diag{a

},N=diag{b

R =diag{r

},S=diag{s

}..

Matrix elements of the oﬀ-diagonal matrix H are identiﬁed as being propor-

tional to the components of the wavetrain envelopes. Operators D

and D

are deﬁned as

Φ = Φ

+ R



x, Φ



, (3.64)

Φ = Φ

+ S



z,Φ



(3.65)

with the constant diagonal matrices x and z. The compatibility condition for

the Lax pair (3.63) is the following (matrix) equation:





−







H, M





H, N



−



RH, N





SH, M



(3.66)

3.7 N-wave equations: example 85

which repr e sents the g e n eral N-wave system. If, for N = 3, we use the (unre-

duced) system of equations (3.66), we get six equations. Assuming that matrix

H is Hermitian, the desired reduction to three equations is obtained. Finally,

− b

21,t

+(a

− a

21,y

=[a

− b

)+a

− b

)

− b

)]H

∗

+[r

− b

)(x

− x

) − s

− a

)(z

− z

)]H

−b

31,t

+(a

−a

31,y

=[a

−b

)+a

−b

)+a

−b

)]H

+[r

− b

)(x

− x

) − s

− a

)(z

− z

)]H

, (3.67)

− b

32,t

+(−a

+ a

32,y

=[a

− b

)+a

− b

)

(−b

+ b

)]H

∗

+[r

− b

)(x

− x

) − s

− a

)(z

− z

)]H

Equations (3.67) have the form o f the three-wave system with asynchronism.

3.7.2 Inclined soliton by twofold DT dressing

of the “zero seed solution”

Plugging (3.64) and (3.65) into (3.63), we can write the Lax pair for (3.67):

+ R[x, Φ]=−λMΦ +[H, M]Φ, (3.68)

+ S[z,Φ]=−λN Φ +[H, N]Φ.

Taking into account the explicit forms of matrices R, S, x,andz,weobtain

ij,t

+ r

− x

)φ

= −λa

+(a

− a

, (3.69)

ij,y

+ s

− z

)φ

= −λb

+(b

− b

where φ

are matrix elements of Φ. The general formula for the twofold DT

(the dressing formula) takes the form

H[1] = H +(μ + μ

∗

)χ, (3.70)

where χ

= φ

∗

/(φ, φ) is built from the columns φ

of the matrix Φ and

(φ, φ) is a scalar product. With H = 0 as a trivial solution of the three-wave

system, i.e., “zero seed solution,” the “dressed” solution of (3.69) is given by

= D

exp [−λ(a

t + b

y) − r

− x

)t − s

− z

)y] , (3.71)

where D

are constants.

We get a soliton solution using the ﬁrst column of Φ:

= D

exp [−λ(a

t + b

y) − r

− x

)t −s

− z

)y] . (3.72)

86 3 From elementary to twofold elementary Darboux transformation

-10

-5 5

-10

-5 5

-10

-5 5

-10

-5 5

0.2

0.4

0.6

0.8

1.2

1.4

Fig. 3.1. Generation of the third wave with account for asynchronism for the time

t =0, 1, 2, 3 (in dimensionless units)

When we have a solution of the t wofold DT in the form of

=(λ + λ

∗

)

∗

(φ, φ)

we can numerically analyze the three-wave interaction. Because the matrix H

is Hermitian it is enough to consider only the coeﬃcients H

, H

,andH

Taking the parameters as λ =1,a

= −1, a

=1,a

=0,b

=1,b

= −1,

=0,r

=0.2, r

= −0.5, r

=0.6, s

=1,s

=0.5, s

=0,x

=0.45,

=0.1, x

=0.6, z

= −0.54, z

=1,andz

=0.6, we get a simulation

of the three-wave interaction in one dimension by the explicit formula (3.72)

(Fig. 3.1). Here y stands for the propagation direction.

It is worth noting that the most important parameter to determine

the properties of the solution is λ, the spectral parameter. P hysically, λ has

the meaning of an amplitude. Much smaller contributions are provided by the

other coeﬃcients (a

, b

, r

, z

, x

,ands

). Let us stress once again that the

interaction without asynchronism pro d u ces only symmetric envelope pulses.

For more details see [272].

3.7.3 Application of classical DT to three-wave system

Let us compare the above results with those that can be obtained by the

method in the previous chapter. Consider an n ×n matrix set {A} and choose

n projectors p

= p

∈{A}, p

=0,i, k =1, 2,...,n. The simplest example

3.7 N-wave equations: example 87

of such a matrix is a diagonal one with the only ith nonzero element that is

equal to 1. A choice of numb ers a

deﬁnes matrices

M =



,N=



The representation of this form is convenient for generalizations to the op-

erator case [267]. The nonlinear equations for interacting waves appear as a

compatibility condition if we start from the pair of ZS equations of the form

= MDΨ +[H, M]Ψ,

= NDΨ +[H, N]Ψ, (3.73)

where the operator D can play the role of abstract diﬀerentiation, realized here

as the commutator with some constant matrix x: DΨ =[x, Ψ]. In analogy

with [354] we represent the potentials of the ZS equations as commutators

[H, M]and[H, N]. Consider ﬁrst the standard DT [324]. The existence of the

classical DT may restrict the choice of the matrices x, M ,andN. For elements

= p

and the obvious choice x =



, we obtain the system

− a

ik,y

− (b

− b

ik,t

(3.74)

=[(a

−a

)(b

−b

)−(b

−b

)(a

−a

)]H

−(H

−x

)(b

−a

) ,

which diﬀers from (3.67) in the last (linear) terms for non-Abelian matrix

elements. The solutions of the system may be constructed by means of the

following proposition [272]:

Proposition 3.18. The system (3.74) is integrable by means of the matrix

Ψ[1] = DΨ − (DΦ)Φ

−1

Ψ,

if Φ and Ψ are solutions of (3.73), when the equality MN = NM holds.

The DT of the matrix H in combination with some gauge transformation is

written as

H[1] = H +(DΦ)Φ

−1

+ A, (3.75)

where A is a matrix that commutes with both matrices M and N. This matrix

is the gauge one guar a nteeing H

[1] = 0. The po ssible choic e of A for diagonal

matrices M and N consists of

A = −diag(DΦ)Φ

−1

Proof. The standard transforms for the potentials [H, M]and[H, N]are

[H, M]+[(DΦ)Φ

−1

,M]and[H, N]+[(DΦ)Φ

−1

,N], with the obvious pos-

sibility to add A to H.

88 3 From elementary to twofold elementary Darboux transformation

If one treats the simplest three-wave case, the compatibility condition

(3.74) is written with more detail. For example, the ﬁrst equation is

12,t

− v

12,y

= n

− k

and similar expr essions exist for the others, with group velocity v

=(b

−b

−a

) and nonlinear constant n

=[(a

−a

)(b

−b

)/(a

−a

)−(b

−b

)].

The coeﬃcient k

=(x

−x

)(b

−a

)/(a

−a

) either deﬁnes attenuation

or can be identiﬁed with the asynchronism parameter ∆k = k

− k

[266, 358]. The last term seems to b e interesting for N-wave systems even in a

matrix case. For example, such a linear term may account for the stimulated

Brillouin scattering/stimulated Raman scattering eﬀects and phase diﬀerences

of waves that appear from the wave asynchronism. Some damping may be

accounted for as well.

The physical systems mentioned appear if the reduction constraint is cho-

sen as H

= H. To preserve the reduction constra i nt during the process

of iterations, we should provide the existence of the hereditary prop erty of

iterations. In other words, Φ should b e chosen to satisfy the condition

x − x

= ΦxΦ

−1

− (Φ

)

−1

. (3.76)

For the unitary matrix Φ

Φ = I, the condition (3.76) simpliﬁes:

x − x

= Φ(x − x

)Φ

−1

, (3.77)

whichissatisﬁedwhenthematrixx is Hermitian. If, further, DΦ = ΦΛ, then

H[1] = H + ΦΛΦ

−1

+ A. (3.78)

Another choice of the matrix Φ is possible via stationary solutions o f the basic

Lax equations with a matrix sp ectral parameter Λ =diag{λ

,...,λ

} so that

= ΦΛ.

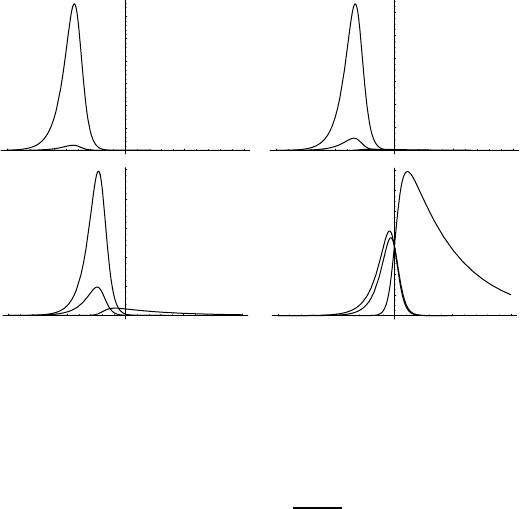
The one-step transformation generates solutions that ar e illustrated by

Figs. 3.2 and 3.3, which give H

(t) for diﬀerent values of the parameters x

3.8 Inﬁnitesimal transforms for iterated Darboux

transformations

The linear dependence on the spectral parameter diﬀerence δ = μ − ν [see

(3.53)] oﬀers an interesting possibility to generate new hierarchies of a com-

bined nonlinear system of potentials and eigenfunctions. The corresponding

equations are obtained by the limiting procedure δ → 0, e.g.,

=[J, P

] ,Ψ

λ − μ

,ζ

ζP

κ − μ

, (3.79)