Додонов А.Г., Ландэ Д.В. Живучесть информационных систем

Подождите немного. Документ загружается.

5.2. Моделирование информационных потоков

161

причем доказано, что оно соответствует решению приведенной

выше системы уравнений для



. Придавая множителю Лагранжа

0 0

log

P e









информационный смысл, можно получить «основ-

ную теорему естественного отбора» Фишера:







Кроме того, доказано, что множитель



пропорционален

«энергопотреблению» популяции.

Таким образом, исходя из эвристического принципа минималь-

ной неожиданности протекания эволюционного процесса, получены

результаты, описывающие динамику отбора в дарвиновских системах,

которые полностью идентичны уравнениям, выводимым из кинетики

размножения и конкуренции, а множители Лагранжа, использующие-

ся для решения вариационной задачи, вполне осмыслены и имеют

прогностическую ценность.

Принцип максимума параметра Мальтуса

Пусть информационное пространство состоит из w информаци-

онных систем. Информационное пространство может быть описано

численностями составляющих его информационных систем

. Пусть

x x





— суммарное количество элементов информационного про-

странства. Допустим, что в течение некоторого локального интервала

времени

-я информационная система характеризуется мальтузиан-

ским параметром

( )



из уравнения

/ .

i i i

dx dt x



 Пусть

i i

p x x



— относительная доля

-й информационной системы в информаци-

онном пространстве. Тогда набор

1 2

{ , ,..., }

p p p p

 назовем струк-

турой информационного пространства; величину

( , )

 



— сред-

ним мальтузианским параметром (

1 1 2 2

( , ) ...

w w

p p p p

   

    ), а

динамика развития размера информационного пространства описыва-

ется уравнением

dx dt x





5. Информационные потоки и вопросы живучести

162

В основе данного подхода постулируется принцип максимума

среднего мальтузианского параметра, т.е. то, что сообщество взаимо-

действующих информационных систем эволюционирует таким обра-

зом, что его средний мальтузианский параметр всегда возрастает, дос-

тигая в устойчивом равновесии своего максимума. В работе [87]

структуры разделяются на вероятные и маловероятные, а также опре-

делены условия, при которых в процессе адаптации из сообщества

элиминируются все популяции, кроме одной или ни одна из популя-

ций не покидает сообщества (в нашем случае информационного про-

странства).

5.3. Нелинейные динамические модели

Известно, что если состояние системы не изменяется во време-

ни, ее называют статической, в противном случае — динамической.

Понятно, что в плане изучения информационных систем основной ин-

терес представляют именно динамические системы: в первую очередь

нас интересуют происходящие изменения, а статические системы ни-

каких изменений не порождают. В свою очередь, динамические сис-

темы делятся на два класса: линейные и нелинейные. Линейными на-

зывают системы, характеристики которых зависят от изменения со-

стояний этих систем. И наоборот, характеристики нелинейных систем

зависят от таких изменений.

Очень часто нелинейные социальные системы проявляют себя,

прежде всего, несоразмерностью отклика на внешнее воздействие.

Хорошо известно, что такие системы могут поразительно легко и без

последствий переносить тяжелые потрясения, и вместе с тем мгновен-

но «пойти в разнос» от малозначимого события или влияния. Именно

информационные операции (инструментом и объектом которых явля-

ются информационные системы) могут рассматриваться как подобное

влияние или воздействие.

Модели, используемые применительно к нелинейным системам,

также называют нелинейными, так как модель — это тоже система, и

она, естественно, может быть нелинейной. Нелинейность модели мо-

жет быть формально выражена в структуре используемых уравнений,

а их решение в некоторых случаях может быть вполне осуществимой

задачей, по меньшей мере, в числовом виде.

5.3. Нелинейные динамические модели

163

Основной акцент при построении нелинейных конкурентных

моделей информационных процессов в настоящее время делается на

анализе принципиальных внутренних взаимодействий динамических

систем на основании логистических моделей. Моделирование дина-

мики развития на основе дифференциальных логистических уравне-

ний широко используется для моделирования самых разнообразных

как естественных, так и информационных процессов.

Естественно, перед применением математических моделей не-

обходимо обосновать их адекватность. Для этого используются хоро-

шо известные методики, в частности, ретроспективный анализ.

Чаще всего для моделирования сложных систем применяют

дифференциальные уравнения, описывающие динамику изменения со-

стояний таких систем. Как правило, это система уравнений первого

порядка, имеющая вид [89]





/ ,

i i

dx dt f X a

 ,

где





,...,

X X X

 — вектор переменных, характеризующих состоя-

ние социальной системы;

— вектор параметров системы;

— время.

Решения приведенной системы уравнений обычно представляют

в виде траекторий в фазовом пространстве. Если фиксировать значе-

ния всех параметров, т.е. выбрать точку в параметрическом простран-

стве, то решения приведенной системы дифференциальных уравнений

будут зависеть только от начальных условий. Однако для качествен-

ного подхода важны не столько частные решения, сколько по возмож-

ности наиболее полное описание поведения системы во всем динами-

ческом пространстве [90].

Эта общая картина будет преимущественно зависеть от значе-

ний, к которым стремяться решения при

 

или при

 

Наиболее важные для рассматриваемой предментой области асимпто-

тические решения такого типа — стационарные точки и предельные

циклы. При этом наибольший интерес представляет специальный вид

устойчивости системы: устойчивость по отношению к изменениям

параметров системы. Система, общий динамический характер которой

не изменяется при малых изменения параметров называется грубой

или «жесткой» (англ. — hard). В противном случае системы называ-

ются «мягкими».

5. Информационные потоки и вопросы живучести

164

Первым шагом при исследовании приведенной выше системы

дифференциальных уравнений является определение стационарных

точек, т.е. решение системы уравнений:





, 0

f X a



Вторым шагом исследований является определение характера

особых точек. Для этого переходят к новым переменным — отклоне-

ниям от координат стационарной точки:

i i i

u x x

 

Вблизи стационарной точки правые части исходных уравнений

системы можно разложить в ряд Тейлора:

0 0

...

i i

i j k l

j k l

m m

f f

u u u u

x x x

x x

 

  

  



Поскольку вблизи

выполняется:



то во многих слу-

чаях можно ограничиться исследованием линейной системы:

i j ij j

u u a u



 





В качественной теории это исследование сводится к определе-

нию собственных значений матрицы коэффициентов

, т.е. к реше-

нию уравнения

ij ij

 

 

В случае, когда все собственные значения



различны и имеют

отличные от нуля действительные части (



), существует «грубая»

5.3. Нелинейные динамические модели

165

стационарная точка. Если все



не равны нулю, то используются

следующие теоремы:

1. Если все

Re 0





, то стационарная точка асимптотически

устойчива.

2. Если хотя бы одно

Re 0





, то стационарная точка неустой-

чива.

Вопрос об устойчивости стационарной точки можно решить

также на основании критерия Гурвица, без непосредственного вычис-

ления собственных значений. Для этого характеристическое уравне-

ние переписывается в виде

1 2 3

0 0 1 1

... 0,

n n n n

a b a b

   

  

    

где

=1.

Матрицей Гурвица называется матрица

-го порядка:

0 1 2 1

0 1 2

0 3

...

0 ...

0 0 ...

. . . . .

b b b b

a a a a

b b b

a a a

b b





Миноры матрицы

(от первого до

-го порядка) называются

определителями Гурвица. Критерий Гурвица заключается в следую-

щем: для того чтобы все

Re 0





, необходимым и достаточным ус-

ловием является положительность всех определителей Гурвица. В ре-

зультате общее исследование характера особых точек исходной сис-

темы может быть основано на приведении ее матрицы к жордановой

форме.

В простейшем случае для системы второго порядка исходное

уравнение может быть записано в виде

 

   

5. Информационные потоки и вопросы живучести

166

где

11 22, 11 22 12 21

a a a a a a



    

Тогда

1,2

4 .

2 2



 

   

В данном простейшем примере ограничимся рассмотрением

лишь грубых стационарных точек. Если ни один из параметров





не равен нулю, то качественная картина фазового пространства в ок-

рестности стационарной точки зависит только от линейных членов и

стационарная точка является грубой. Существуют три грубые поло-

жения равновесия:

1. Стационарная точка типа «узел» (рис. 31, а): собственные зна-

чения



действительные, одного знака,

0 , 0.



   

При





узел устойчивый, при





— неустойчивый.

2. Стационарная точка типа «седла» (рис. 31, б): собственные

значения



действительные, разных знаков,

0, 0.



  

3. Стационарная точка типа «фокус» (рис. 31, в): собственные

значения



комплексные,

, 0.



  

При





— устойчи-

вый фокус, движение около стационарной точки носит характер зату-

хающих колебаний. При





фокус неустойчивый, возникают коле-

бания нарастающей амплитуды.

Рис. 31. Фазовые портреты грубых особых точек

5.3. Нелинейные динамические модели

167

Анализ фазовых траекторий позволяет сделать заключение о ха-

рактере эволюции системы, определять области ее детерминированно-

го поведения и области бифуркаций (т.е. области значений парамет-

ров, при которых возникает неустойчивость и происходит изменение

вида решений уравнения, описывающего поведение системы).

Сложные системы часто имеют несколько устойчивых состоя-

ний (аттракторов), в одном из которых они рано или поздно оказыва-

ются. В этих случаях пути эволюции не дискретны: возможен лишь

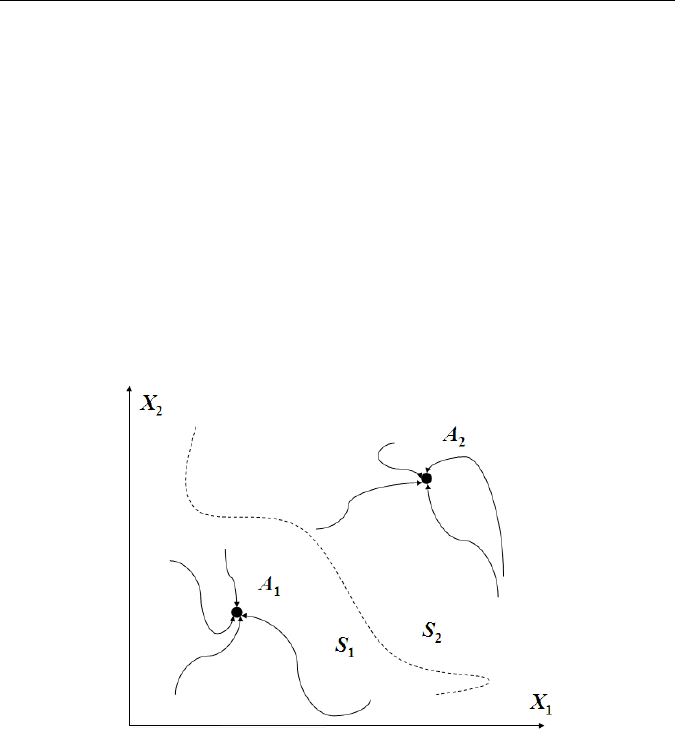
определенный набор путей, соответствующих аттракторам (рис. 32).

При этом переходы от одного аттрактора к другому не могут произой-

ти самопроизвольно, для этого необходимо изменение внешних усло-

вий или свойств системы. В частности, в социальных системах именно

для этого применяются информационные операции.

Рис. 32. Пример фрагмента фазового пространства динамической системы

(плоскостной срез по двум координатам Х

и Х

(А

и А

— аттракторы,

и S

— соответствующие области притяжения аттракторов)

Из синергетики известно, что переход системы из одного со-

стояния в другое проходит фазу хаоса при ослаблении структурообра-

зующих процессов. В информационных системах хаос обеспечивает

систему первоначальным набором вариантов дальнейшего развития —

аттракторами. В периоды хаоса, кризисов, когда возникают возмож-

5. Информационные потоки и вопросы живучести

168

ности многовариантного развития, информационные операции приоб-

ретают решающую роль. В эти периоды социальные и информацион-

ные системы наиболее уязвимы относительно информационных воз-

действий, которые могут сыграть решающую роль в дальнейшем раз-

витии событий [89], выборе того или иного аттрактора.

Таким образом, можно констатировать, что на разных стадиях

эволюции информационные системы обладают различной чувстви-

тельностью и уязвимостью к внешним воздействиям — информаци-

онным операциям, которые становятся наиболее опасными в периоды

хаоса — кризисов. В этих случаях даже не слишком интенсивные ин-

формационные воздействия могут задать направление развития сис-

темы и повлиять на характер ее последующей эволюции. Безусловно,

как и для эффективного проведения информационных операций, не-

обходимо знать структуру имеющихся аттракторов, а также владеть

набором приемов перевода системы от одного аттрактора в другой.

Рассмотрим конкретные нелинейные модели динамики инфор-

мационных систем, начиная с простейшей модели роста (

x kx





), ко-

торая была предложена Мальтусом для расчета динамики численно-

сти населения Земли. Эта модель ведет, как было показано выше, к

экспоненциальному возрастанию населения

во времени; она может

быть применима, например, к развитию информационных систем на

начальном этапе. Решением приведенного уравнения, как известно,

является экспонента.

Очевидно, ни один реальный процесс — ни физический, ни ин-

формационный, не может развиваться по экспоненциальному закону

неограниченное время. Действительно, начиная с некоторого момента,

зависимость слишком быстро стремится к бесконечности, которая в

природе, по понятным причинам, не реализуется. Следовательно, при-

ходится признать, что рано или поздно, и скорее рано, чем поздно,

произойдет некоторая катастрофа, которая изменит характер зависи-

мости и вернет ее в рамки допустимого интервала значений.

В более или менее стабильных системах всегда присутствует

элемент самосогласованности, в силу чего на значительных проме-

жутках времени зависимость динамики их развития описывается бо-

лее сложными уравнениями, содержащими обратные связи. Поэтому

характер зависимости со временем изменяется, причем изменения

происходят не тривиальным образом. В результате возникают сле-

дующие типичные случаи:

5.4. Взаимодействие информационных систем

169

— зависимость достигает насыщения, и система переходит в

статическое (или, возможно, гомеостатическое) состояние;

— зависимость имеет локальный максимум, за которым следует

убывание (в том числе и до нуля);

— устанавливается колебательный режим (обычно затухающий,

но возможен и автоколебательный).

В реальной жизни, как правило, динамические системы облада-

ют достаточно эффективными обратными связями, позволяющими

корректировать характер происходящих в них процессов и тем самым

удерживать их в определенных рамках. Информационные операции,

корректируя эти обратные связи в определенные периоды эволюцион-

ного процесса, могут достаточно эффективно повлиять на характер

поведения всей системы.

Как и в случае информационных потоков, используется широко

применяемое обобщение закона Мальтуса, известное как логистиче-

ская модель.

5.4. Взаимодействие информационных систем

Логистическое уравнение описывает динамику одной информа-

ционной системы, взаимодействующей только с окружающим инфор-

мационным пространством. В теории популяционной динамики раз-

работана классификация различных форм такого взаимодействия по-

пуляций [91–93], в нашем случае — информационных систем.

К основным информационным системам относятся следующие:

— нейтрализм (отсутствие прямого воздействия популяций друг

на друга);

— конкуренция (взаимное подавление популяций);

— амменсализм (одностороннее подавление одной популяции);

— хищничество (уничтожение особями одной популяции осо-

бей другой);

— симбиоз (продуктивное сосуществование популяций).

В динамике взаимодействующих популяций выделяются две ка-

тегории воздействий, отличающиеся временным характером:

— фазовые (однократные);

— параметрические (постоянные).

Логистическая модель позволяет вполне удовлетворительно

описывать и динамику

взаимодействующих между собой популя-

5. Информационные потоки и вопросы живучести

170

ций. В общем случае это осуществляется с помощью уже приведенной

для случая информационных потоков системы уравнений, но с не-

сколько иным смыслом параметров:

( )

( )[ ( )],

(0) .

i i ij j

i i

dn t

n t p q n t

n n



 





Тип процесса, описываемого этой системой уравнений, опреде-

ляется значением и знаком коэффициентов

. Следует также

учитывать, что в каждом уравнении диагональные члены

( ) ( )

i j

n t n t

описывают внутривидовое взаимодействие, а перекрестные

( ) ( )

i j

n t n t

— межвидовое.

Иными словами, диагональные члены описывают влияние на

популяцию внешней среды, в том числе исчерпание доступных ресур-

сов, а перекрестные — воздействие одной популяции на другую (по-

ложительные значения соответствуют благоприятному влиянию, от-

рицательные — неблагоприятному). Коэффициенты

имеют смысл

скоростей увеличения соответствующих популяций при отсутствии

взаимодействия.

Важным моментом является также поведение популяции при

заданных значениях параметров и в отсутствии взаимодействия (на-

пример, ее рост ограничен сам по себе).

Приведенная выше система уравнений в принципе может опи-

сывать широкий спектр зависимостей, и это, в определенном смысле,

является проблемой, так как при желании из ее решений можно «вы-

тащить» все что угодно. Поэтому работа с ней требует взвешенного и

ответственного отношения.

Однако решения, характеризующие реальные процессы, обычно

относятся к одному из следующих режимов:

— стационарному;

— автоколебательному;

— квазистохастическому.