D?m?si P., Nehaniv C.L. Algebraic Theory of Automata Networks. An Introduction
Подождите немного. Документ загружается.


6.3. Homomorphic Completeness
Under
the
Primitive
Product
1 81
letter
=
(z
1
,...,
Z6n)
€ X^, and t (=
1,...,
18ns)',
we
have
It
is
easy
to
check that
N is a
primitive power
of
.A;
moreover, whenever
, (1 t
18ns)
really depends
on its
input variable, then
it may
additionally depend only
on its tth
state variable
and at
most
one
other state variable. Therefore,
N has the
properties required
by
Proposition
6.3 for the
last component
of M.
Denote
by S
N
the
transition
function
of N and
consider
the
automaton
C
given
in
Lemma 6.12. Observe that whenever
N is in the
state having
the
form
(w
\
1
,...,
w\
x
,
by
the
effect
of
words
having
the
form
if
and
only
if
Therefore,
using
the
short notation
bk
for
the
state
b
k
of
N, by
Lemma 6.12
we
have that there exists
a
pos-
itive integer
m
having
the
following property.
For
every transformation
v on
{b
1
,
...,b
n
],
there exists
a
word
such
that
for
all
Every
n-state automaton
£ is
isomorphic
to a
subautomaton
of an
n-state automaton
D
with
the
following properties:
(1)
For
each transformation
r of the n
states
of D,
there
is an
input letter
X
Y
inducing
y.
(2)
There
are at
least
as
many distinct letters
of D
that induce
r as
there
are
that induce
y
in .
Thus,
to
complete
the
proof,
it
suffices
to
establish
the
result
for the
following
n-
state automaton having these properties whose states
are a
subset
of
those
of N. Let
D = (D,
X
D
),
<$
D
)
D =
{b
1
,...,
b
n
], where
b
k
, k =
1,...,n,
are the
states
of N
discussed
before.
For
each transformation
r of
\b\,...,
b
n
} let
there
be an
input letter
X
Y
of D
having
D(b
k
,
X
y
)
= r
(b
k
),
k =
1,...,
n.
Furthermore,
let
there
be at
least
as
many
letters
of D
which
induce each given transformation
r as
there
are in £.
We
shall show that
D can be
represented homomorphically
by a
primitive power
of
A.
Clearly,
{8D(b
k
,
x) I b
k
D, x X
D
] = D.
To
each length
ms
input word
p =
x\...
x
ms
of D, we
associate
the
transformation
v
n
induced
bv
this word
on the set D = (b
1
b
n
}.
Define,
following Lemma 6.12,
The
mapping
n
>
• ""
»»*•
satisfies

1
82
Chapter
6.
Primitive
Products
and
Temporal
Products
For
every
d > 0 and a a
state
of N, (p, q) € R ,d, P €
(XD)
ms
,
we
clearly have,
whenever
N(a,
q) D,
that
8D(8N(a,
q), p) =
8j^f(a,q
(p))
D).
Furthermore,
by
taking
t to be a
letter
of X
D
inducing
the
identity under
$
D
(that
is, S
D
(bi,
t) =
b
i
{
for all
b(
D) and
letting
q be (
(t
m5
))
;
with
msj <
ms+d
and p =
L
d
-
ms(j-1)
implying
(p, q)
R
t
d, we
derive
8
D
D(8
N
(b
i
,q),
p) =
<5p(b
i
,,
p) = b
t
.
Therefore,
D =
[8
D
(8
N
(a,
q), p) \
a a
state
of
N,(p,q)
R ,d,
(a,q)
D}.
This shows that conditions
(1) and (2) of
Lemma 6.11 hold.
For
every
i (=
1,...,
6n),
define
:
(XD)
ms
A
ms
as
follows:
for
each
1
j ms, the jth
letter
of
,(/?)
( €
(XD)
mj
)
is
equal
to the ith
component
of the jth
letter
=
(Zj,i,
• •.,
Zj,6n)
of
(/>). Therefore,
as in
Lemma 6.11 (taking
i and n of
the
lemma
to be 6n and ms,
respectively),
we can
construct
the
product
V = R
i!
x
•
• • x R
r6n
x
N(X
D
,
{,...,
(
6n
,
n+i) which homomorphically represents
D.
By
Lemma 6.9, given
an
integer
d
|X
D
|
ms
,
for
each
i =
1,...,
6n, we
obtain
a
primitive power
Mi
of
A
such that apart
from
its
last one,
its
feedback functions
do not
depend
on the
last state variable,
and
furthermore,
Mi
v-represents
.
|
.
)
.
Now
set
^fi(m\,...,
m
6n
,
m
6n+1
,
x) = x for
each
i =
1,...,
6n and
6n+1
(m1,
..., m
6n
,
m6n+1,x)
=
(z1,...,
Z6n)>
where
x € XD,
zi,
is the
state
of the
last
factor
of Mi
(which
represents
i
,d)
for 1 i 6n, and m
6n+i
is the
state
of N. By
Proposition
6.8
(considering
, X
D
, 6n to be M, X, m of the
proposition),
we
obtain
M = M\ x • • • x
M6n
x
A/"(XD,
1,
...,
6/i+i)»
which homomorphically represents
V,
hence
,
hence
.
On
the
other hand, observe that
we
have
the
conditions
of
Proposition
6.3 for the
product
M
(taking
, X
D
, 6n to be
M
n+1
,
X, n of the
proposition).
By
Proposition 6.3,
M is
isomorphic
to a
primitive power
P of A
Therefore,
8 is
homomorphically represented
by
the
primitive power
P.
This completes
the
proof.
Corollary 6.14.
Let K. be a
class
of finite
automata.
If
1C
satisfies
Letichevsky's crite-
rion,
then
K, is
complete with
respect
to
homomorphic
representations
under
the
primitive
product.
By
the
Letichevsky decomposition theorem (Theorem 2.69),
a
class
of finite
automata
is
complete with respect
to
homomorphic representations under
the
Glu§kov product
if and
only
if it
satisfies Letichevsky's criterion. Therefore,
one
obtains
the
following statement.
Theorem
6.15.
Suppose
that
1C
is a
class
of finite
automata.
Then
the
following
statements
are
equivalent:
(1)
satisfies
Letichevsky's
criterion.
(2)
1C
is
complete with
respect
to
homomorphic
representations
under
the
Gluskov
prod-
uct.
(3) k is
complete with
respect
to
homomorphic
representations
under
the a
i
,
-product
for
all
i 2.
(4) k is
complete with
respect
to
homomorphic
representations
under
the a
i
,
-product
for
some
i 2.
(5)
1C
is
complete with
respect
to
homomorphic
representations
under
the
V
j
-product
for
all j 3.
(6)
1C
is
complete with
respect
to
homomorphic
representations
under
the
Vj-product
for
some
j 3.
(7) k is
complete with respect
to
homomorphic representations under
the
-Vj-product
for all 2, j 3.
(8)
1C
is
complete with respect
to
homomorphic representations under
the
a
i
-V
j
-product
for
some
i 2, j 3.
(9) K, is
complete with respect
to
homomorphic representations under
the
primitive
product.
Remark.
Theorem 3.36 implies that there exists
no finite
class
of
automata which
is
complete
with respect
to
homomorphic representations under
the a
\
-product.
Therefore,
by
Theorems
2.69
and
5.9, there
is a
class
of finite
automata
satisfying
Letichevsky's criterion which
is
complete with respect
to
homomorphic representations
for
neither
the
a
1
-product
nor the
V2-product.
This shows that
the
above result
is
sharp.
6.4
Temporal
Products
Let A = (A, Y, 8) be an
automaton
with
Y = X
k
for
some
nonempty
finite set X and
positive
integer
k. We say
that
A is a
k-channel automaton (with
respect
to X). If
there
exists
a
(one-
channel)
automaton
A' = (A, X, )
such that
for
every
pair
a € A,
(x
1
,...,
x
k
) X
k
, we
haveS(a,
(x
1
,..
.,x
k
))
=
S'(a,
x
1
..
.X
k
);ihenitissaidthatAhas
a
one-channel analog
A.
Thus
A'
isomorphically
simulates
A in
equal
lengths
under
( , ),
where
\ : A A and
T2
: X
k
X* are
defined
by (a) = a,
2((xi,...,
X
k
) = x
1
...x
k
.
If .
A'
is a
product
of
automata,
then
.A is a
simple
type
of
temporal
power
of
this
product
(defined
below).
In
this
case,
the
components
of
this
structure
A are fixed
during
its
work.
In the
general
case
of
tem-
poral
products,
the
internal
structure
of
A
will
be
allowed
to
change
cyclically
as it
operates.
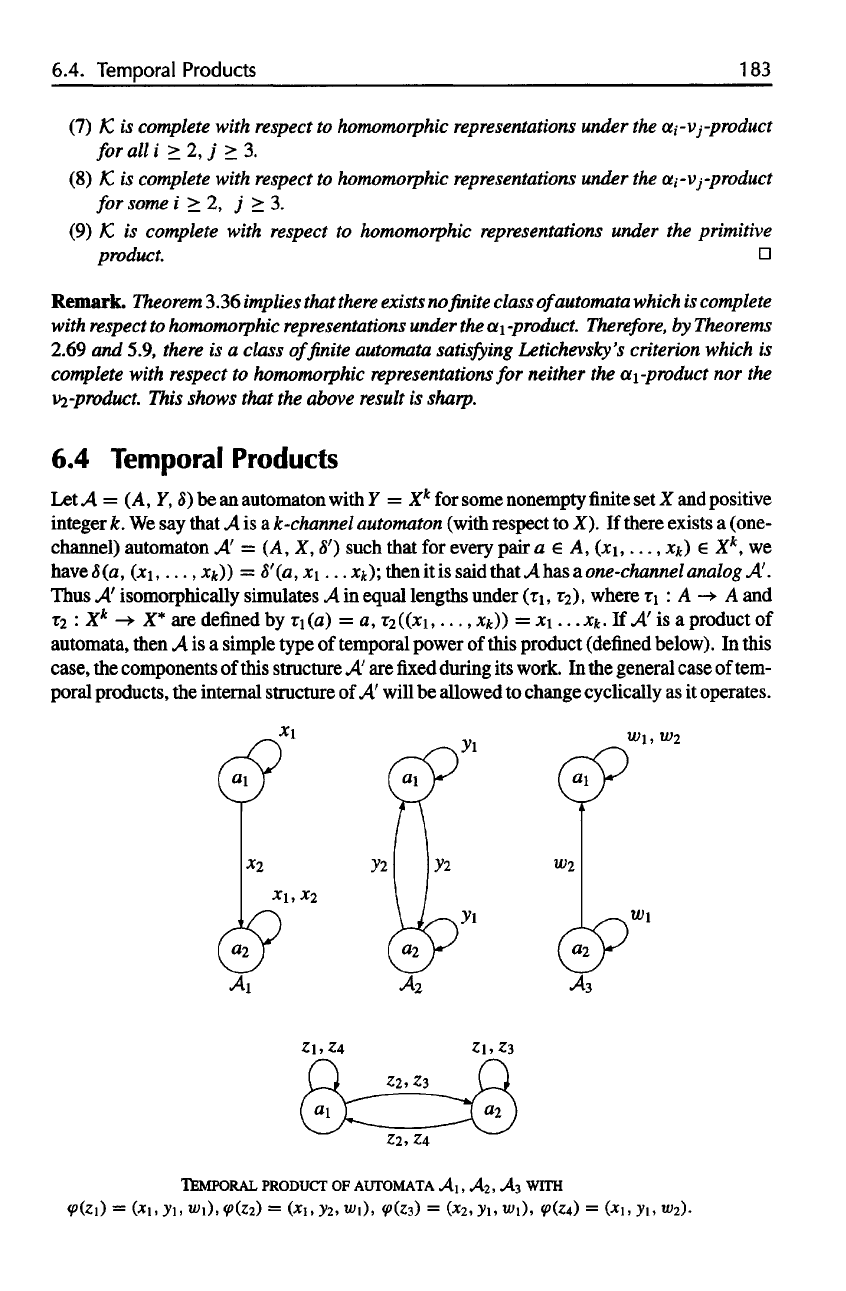
TEMPORAL
PRODUCT
OF
AUTOMATA
A
1
,A
2
,
A
3
WITH
184
Chapters. Primitive
Products
and
Temporal
Products
We
will
see
that
the
temporal compositions
of the
general product
and the
cascade
product
can be
represented
by
very simple models
of finite
automata networks which
are
cyclically able
to
modify
their inner structures.
We
will show that, despite their simplicity,
they
have
a
very strong completeness property.
Let
A
t
=
(A
t
, X
t
,8
t
),t
= 1, 2, be
automata having
a
common state
set A (= AI =
A
2
).
Take
a finite
nonvoid
set
X
and a
mapping
of
X
into
X\ x X
2
.
Then
the
automaton
A =
(A, X, 8) is a
temporal
product
(t-product)
of
A
I
by A
2
with respect
to X and ( if for any a
A and x X,
8(a,
x) =
8
2
(8
1
(a,
x\), x
2
),
where
(x\,
x
2
) =
(x).
The
concept
of the
tem-
poral
product
is
generalized
in the
natural
way to an
arbitrary
finite
family
of n > 0
automata
A
t
(t =
1,...,
n), all
with
the
same
state
set A, for any
mapping
( : X "=1 X
t
by
defining
8(a,
x) = 8
n
( • •
82(8
1
(
a
,
x
\
),
x
2
),...,*„)
when
(x} =
(x\,...,
x
n
).
In
particu-
lar,
a
temporal product
of
automata with
a
single
factor
is
just
a
(one-to-many)
relabeling
by
X
of the
input
letters
of
some input-subautomaton
of its
factor
or,
equivalently,
a
quasi-direct
product with just this factor. Note that
the
formation
of the
temporal product
is
associative.
We
apply
the
notation -product
for
each
of the
following concepts, respectively:
g-product, -product, q
i
-product, o-product, t-product. Given
a
class
1C
of
automata,
the
notions
(k), H(k), s(k),
P (k)
stand
for the
class
of all
isomorphic images
for
k, all
homomorphic images
for k, all
subautomata
for k, and all
-products
for k, re-
spectively.
We
define
the
(left)
multiplication
of
these operators
as
usual
in the
literature.
For
any
sequence
O
\
,...,O
n
of the
discussed operators
we
write
O\...
O
n
(k) instead
of
O
1
(O
2
(...
O
n
(k)...)).
Moreover,
we use the
short notion
T for S
P
t
IPp.
Let us first
consider some simple examples:
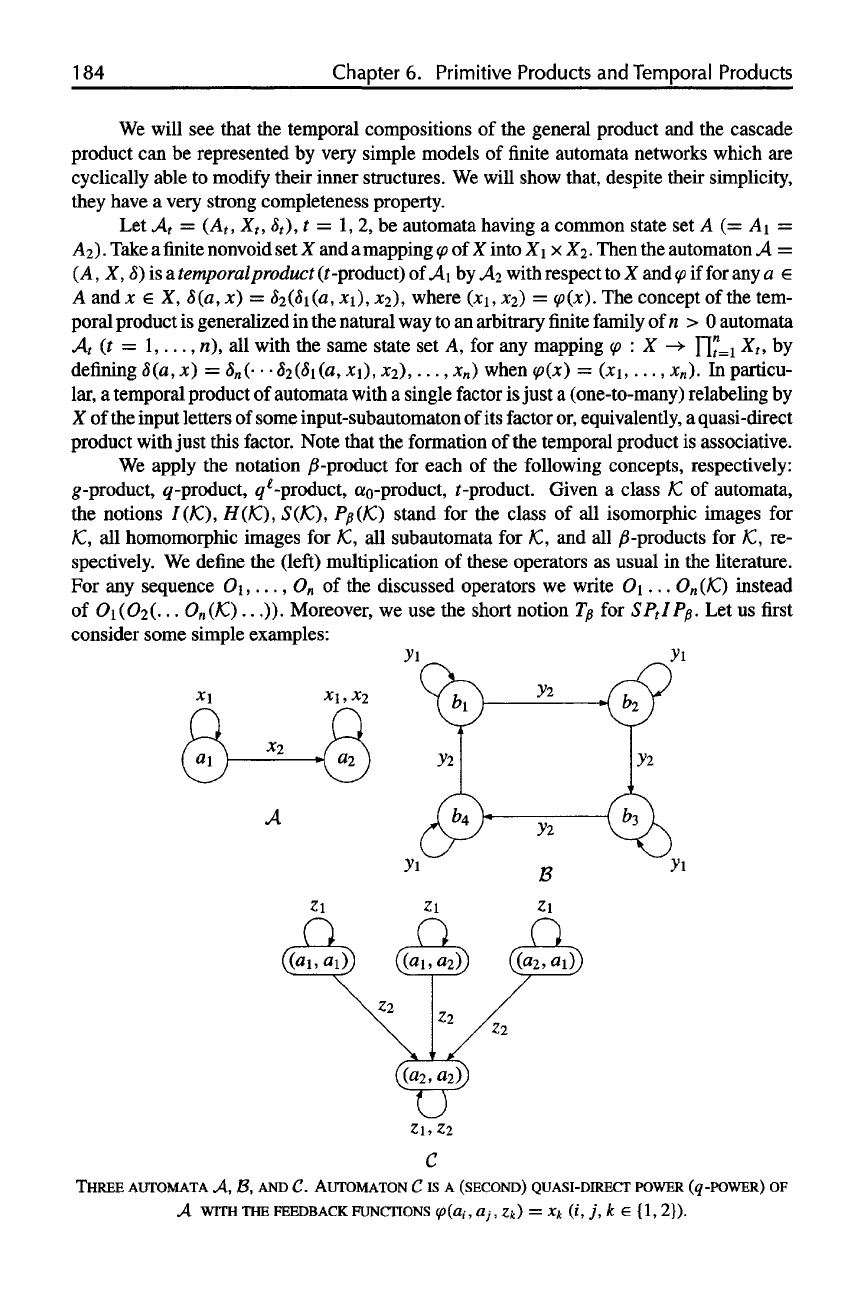
THREE
AUTOMATA
A. B.
AND
C.
AUTOMATON
C is A
(SECOND) QUASI-DIRECT POWER a-POWER)
OF
A
WITH
THE
FEEDBACK
FUNCTIONS
6.4.
Temporal
Products
1 8 5
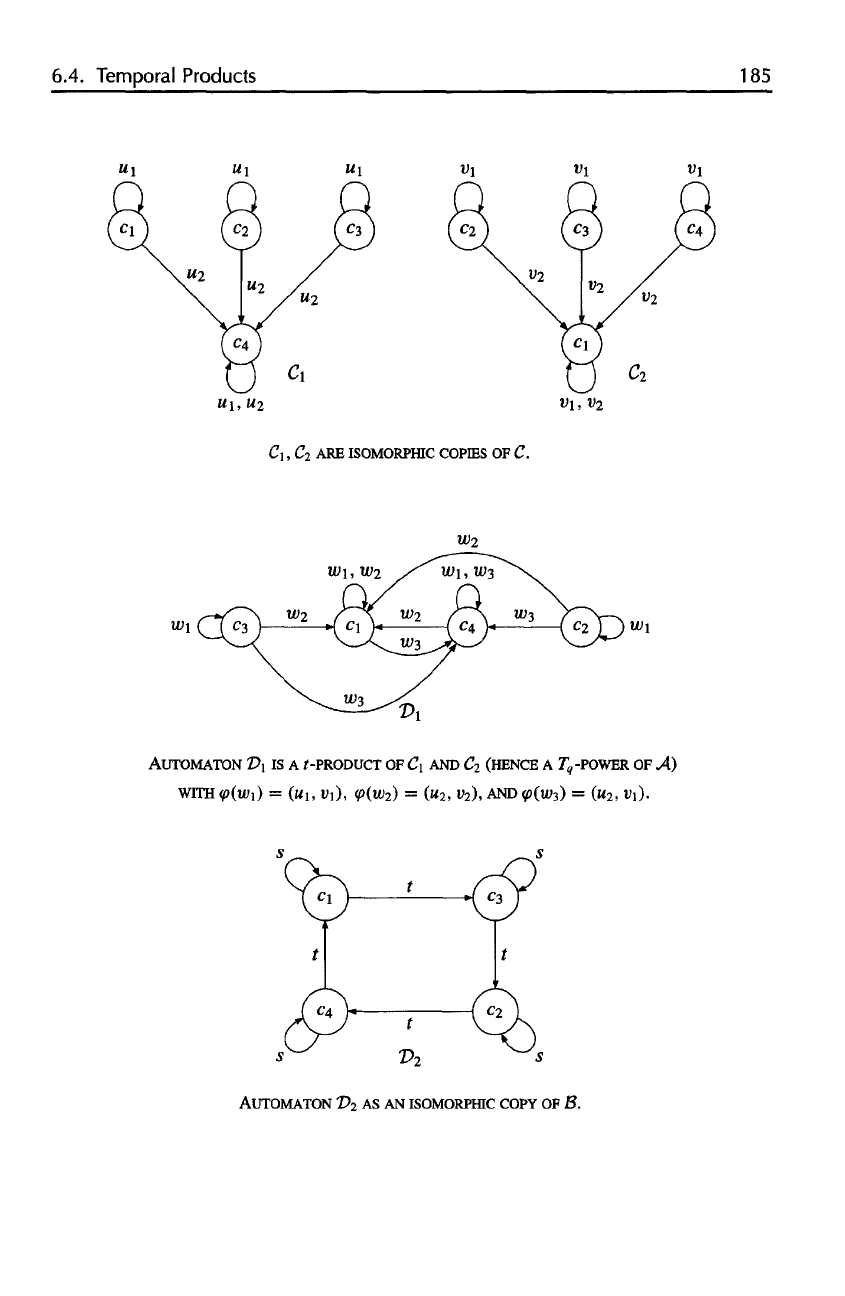
C
\
,
C-
2
ARE
ISOMORPfflC COPffiS
OF C.
AUTOMATON
D
1
is A
t-PRODUCT
OF C
\
AND
C-
2
(HENCE
A T
a
-POWER
OF A)
WITH
,
AND
AUTOMATON
D
2
AS AN
ISOMORPHIC COPY
OF B.

186
Chapter
6.
Primitive Products
and
Temporal Products
t-PRODUCT
OF D
2
BY
D
\
(HENCE
A T
q
-PRODUCT
OF A
AND
B)
WITH*
AND
BI
IS A
q-PRODUCT
OF A
\
, A
2
WITH
THE
FOLLOWING VALUES
OF ITS
FEEDBACK FUNCTION
AND
B
2
IS
AN
ISOMORPfflC COPY
OF B.
6.4.
Temporal
Products
1 8 7
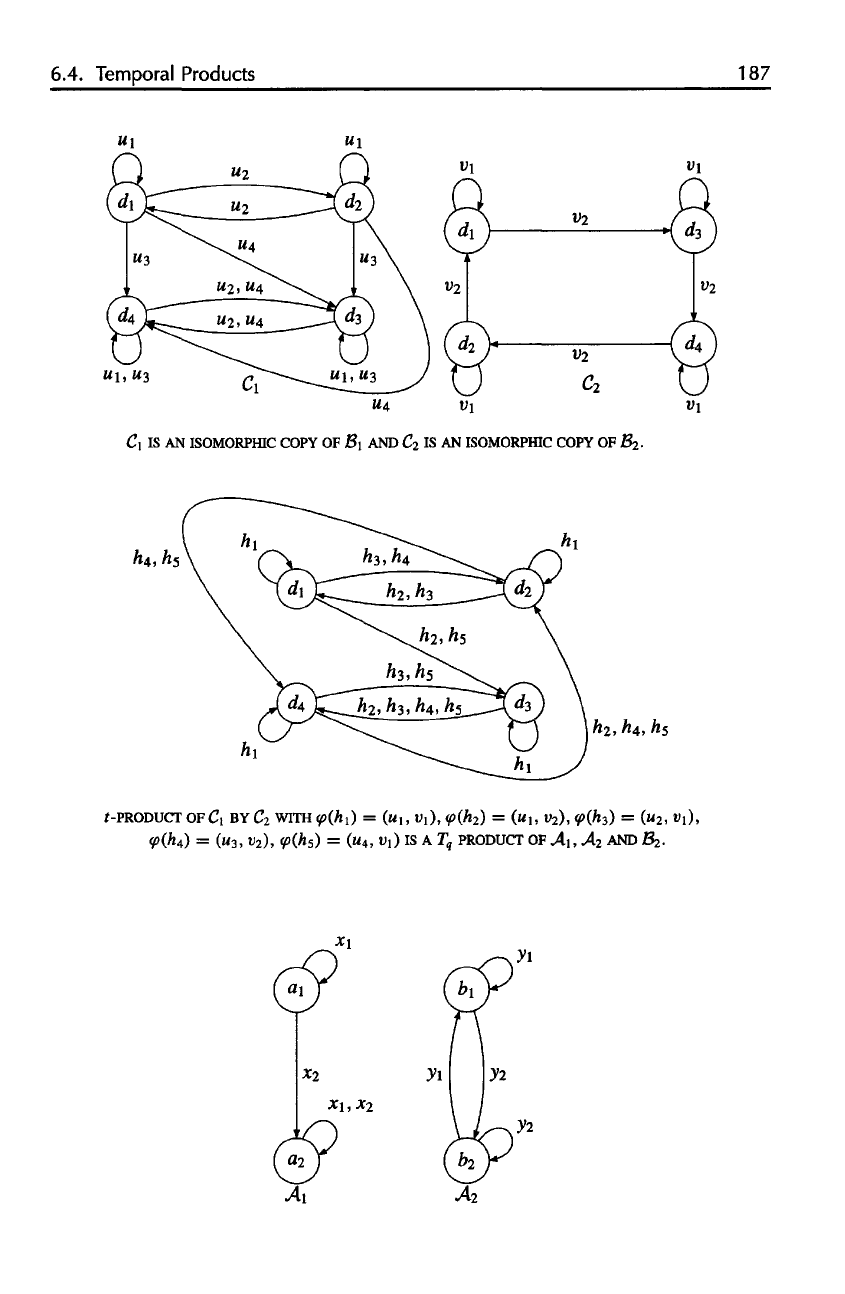
C\ IS AN
ISOMORPfflC COPY
OF B
\
AND C
2
IS AN
ISOMORPfflC COPY
OF B
2
.
t-PRODUCT
OF C
1
BY C
2
WITH
PRODUCT
OF
A
\
, A
2
AND
B
2.
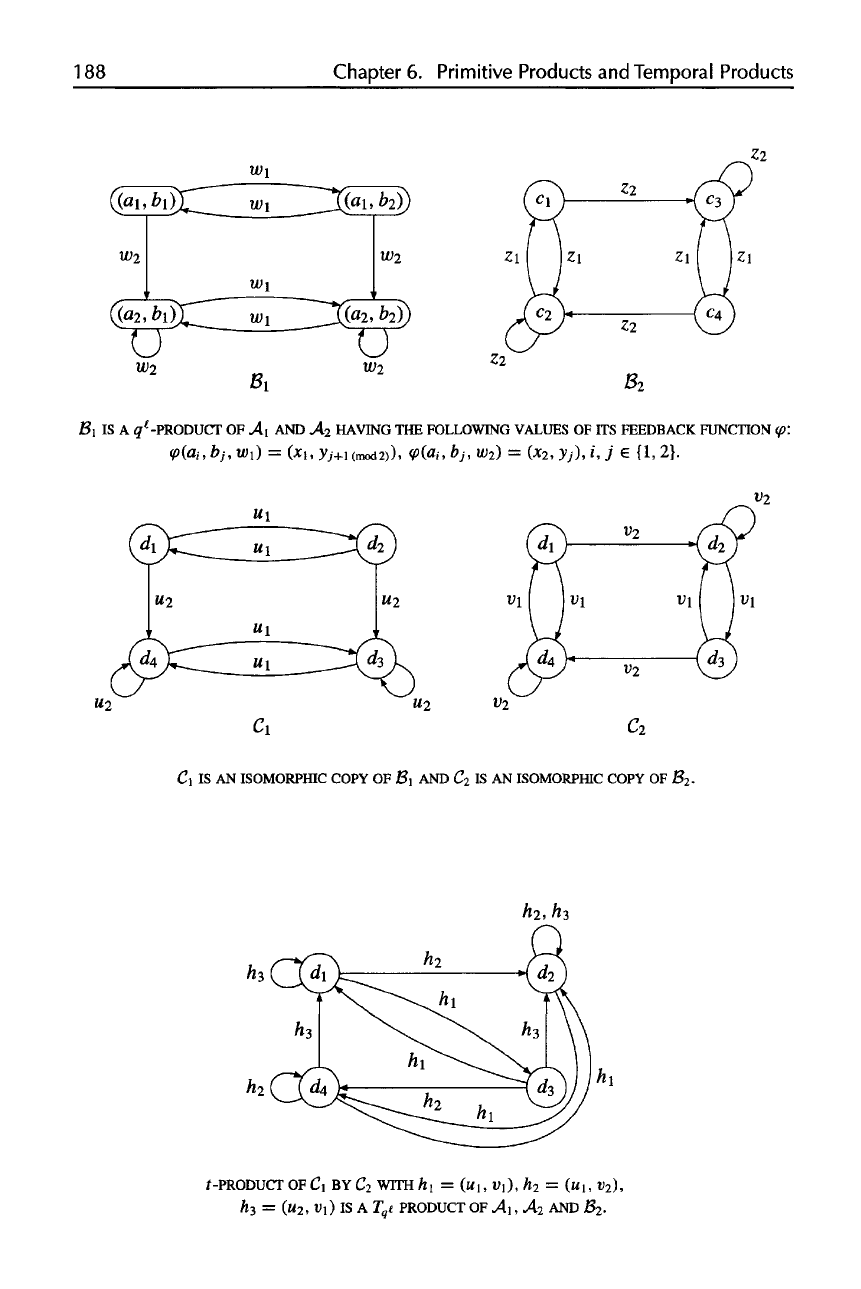
188
Chapter6.
Primitive Products
and
Temporal Products
BI
IS A
q
e
-PRODUCT
OF A\ AND
A
2
HAVING
THE
FOLLOWING VALUES
OF ITS
FEEDBACK FUNCTION
C\
IS AN
ISOMORPHIC
COPY
OF
B
}
AND
C
2
IS AN
ISOMORPHIC
COPY
OF
B
2
.
f-PRODUCT
OF C\
BYC
2
WITH/I
i
=
(HI,
t>i),
h
2
=
(MI,
t^),
h
3
=
(U
2
,
U])
IS A
T
q
t
PRODUCT
OF
A\,
A
2
AND
B
2
.

6.4. Temporal Products
189
Let K,
again
be a
class
of
automata.
We say
that
the
automaton
A is a T
B
-product
of
automata
from
K if A E
7>(K)
(= S
PtIP
B
K
).
It is
said that
K. is
complete with respect
to
homomorphic
(resp.,
isomorphic) represen-
tations under
the
T
B
-product
if
HT
B
(K)
(resp.,
7^(K))
is the
class
of all
(finite) automata.
(Note that
/S7>(K)
=
T
B
(K)
and
HST
B
(K
=
#7>(K)
hold
for
every
class
of
automata.)
Now
we
study
the T
-product.
Theorem
6.16.
The
following statements
are
true:
(1) An
arbitrary
T
-product
of
autonomous automata
is an
autonomous automaton.
(2) An
arbitrary
T
-product
of
permutation automata
is a
permutation automaton.
(3) An
arbitrary T
q
-product
of
reset automata
is a
reset automaton.
Let A — (A, X, 8) be an
automaton
and
define
for any x E X the
automaton
A
x
=
(A,{x
0
,x},
x
)
such
that
X
0
x is an
arbitrary
symbol;
moreover,
8
x
(a,
X
0
)
= a and
x
(a,x)
= (a, x) (a € A).
Lemma
6.17.
Let
1C
be a
class
of
automata which contains
an
automaton
B
with
A
x
6
SP
t
({B}),
X E X.
Then
A &
SP
t
(K).
Proof.
Let M
x
= (M,
{X
0
,X},
S'
x
)
€
P
t
(B),
x e X, be
automata with
A
x
e
S({M
X
}).
Moreover,
let
x
1
,...,
x
n
be an
arrangement
of the
elements
of X.
Take
the
temporal product
M = M
Xl
x • • • x
M
Xn
(X,
)
such that
for any x
t
E X,
(x
t
)
=
(z
1
,
x
,,...,
z
n
,
x
,),
where
z
1
,
x
,
= • • • =
z
t
-i,
x
,
=
z
t
+i,
x
,.
•.
z
n
,
x
,
=
XQ
and
z
t
,
x
,
= x
t
. It is
clear
that
A is a
subautomaton
of M
Lemma
6.18.
Let
1C
be a
class
of
automata having
a
(not necessarily
different)
pair
A
t
=
(A
t
,
X
t
,
t
),t
=
1,2,
of
elements with
the
following properties:
(1)
There
is a
pair
a € AI, x e X\
with
a
1(a,
x).
(2)
There
is a
triplet
a
1
, a
2
€ A
2
, y € X
2
with
a
1
a
2
and
($2(01,
y)
82(a
2
,
y).
Then
for any
positive integer
m
there
can be
found
an
automaton
M = (N, X, 8)
€
P
q
(JC),
pairwise
disjoint
sets
B\,...,
B
2m
_
m
C N, and
(not necessarily
different)
inputs
yi,
y2,xi,...,x
s
€ X,s > 1,
such that
B
m+t
=
{b
m+t
,b
m+t
(l)
...
,b
m+l
(s)
},8(b
(K)
+t
,x
k
)
=
b
m+t
,
k=l,...,s,
b
m+t
[b
(1)
m+1
,...,
b
(s)
+t,},
t =
1,...,
m.
Moreover,
(la)
if
1C
contains
a
nonautonomous automaton, then
for any t =
1,...,
m,
(b
t
,yi)
(b
t
,
3*2)
(and thus,
yi
y
2
);
(2a)
if
1C
contains
a
nonpermutation automaton, then
y
2
= x\ = • • • = x
s
, s = m +
1,
\B
m+t
\
= m + 2, t =
1,...,
m; and
(3a)
if
1C
is a
class
of
permutation automata which
has a
nonautonomous automaton, then
s
=
2,*i
=yi,x
2
=
y2,xi
/ x
2
,
B
m+t
\
= 3,t =
1,...
,m.
Proof.
For a
suitable
system
V\,...,
Dr €
AC
of
automata construct
a
quasi-direct product
D
1
x • • • x
D
r
(X,
<p)
and
suppose that
r is a
sufficiently
great
number
for the
properties
as
we
define
in the
following
investigations.

190
Chapter
6.
Primitive
Products
and
Temporal
Products
First
we
prove that
for a
suitable
M
there
are
pairwise disjoint sets
B\,...,
B
2m
^ N
such
that
b
t
(b
t
,
yi
),8(b
t
,y
2
)},8(b
(
V
+t
,x
k
)
=
b
m+t
,
b
m+t
i
{b
(
»
+t
,...
,b%>
+t
},t
=
1,...,
m, k =
1,...,
s.
(Note that
the
special cases
y\ = y
2
and s = 1 are
allowed.)
Let
T>\
= AI and
Cc')
= x, x' e X. (If
there
is no
danger
of
confusion, then
we
omit
the
arguments
of any
feedback
function
on
which
it
really does
not
depend.) Then
for
an
arbitrary
(a, d
2
,
...,d
r
)
e N and x' e X, the first
component
of
8((a,
d
2
,...,
d
r
),
x') is
8i(a,
x).
Thus,
if we
suppose that
for
every pair
b' e
{b
u
}(J(B
m+u
\
{b
m+u
}),
u =
1,...,
m,
b"
e (B
v
\
{b
v
})
U
{b
m+v
},
v =
1,...,
m, the first
component
of the
vector
b' is
equal
to
a
and the first
component
of the
vector
b" is
equal
to
8i(a,
x),
then
we
obtain
b' b".
Since
D
1
= A\ and
(x'}
= x, x' e X,
this assumption does
not
lead
to a
contradiction
even
if
8(b',
x') = b" for an x' e X (by u = v and b', b" € B
u
or b', b" e
B
m+M
).
Therefore,
for a
suitable
W and
B
1
,...,
B
2m
c
AT
we get
that [b
u
,
b
(
1)
v
,...,
b
(s)
+v
}
and
[8(b
u
,
x'),
8(bn+v,
x'),...,
8(b^
+v
,
x')},
x' e X, u, v =
1,...,
m, are
pairwise disjoint
sets.
(In
particular,
if u = v,
then
we
also have this
fact.)
Thus,
if we
prove that there
are
pairwise disjoint sets
B\,...,
B
2m
c N
having these properties, then
the first
part
of
our
lemma
is
shown. (Naturally,
yi = y
2
and s = 1 are
possible.)
If b' —
b
m+u
,
b" =
bm+v,
1 < u < v < m,
then suppose
the
existence
of an
appropriate
z e
{1,...,
r}
for
which
D
z
= A
2
,
{d
z
,
d'
z
}
=
{8
2
(ai,
y),
8
2
(a
2
, y)}, where
d
z
and d'
z
denote
the zth
components
of
b' and b",
respectively. Then
we
obtain
b' b" by
(2).
It
remains
to
study
the
case
b'
e
{b
u
}\J(B
m+u
\{b
m+u
}),b"
e
{b
v
}\J(B
m+v
\{b
m+v
}),
1 < u < v < m.
Thenassumethe
existence
of an
appropriates
6
{1,...,
r} for
which
D
z
= A
2
,
{d
z
,d'
z
}
=
{a
1
,a
2
},
where
d
z
and
d'
z
denote
the zth
components
of b' and b",
respectively. Then
we
obtain again
b' ^ b"
by
(2).
For
every
x' € X, let
z
(x'}
= y in
both
of the
above
cases.
Thus,
for
every pair
b'
e{b
u
}(J (B
m+u
\
{b
m+u
}),
b" e
{b
v
}
U
(B
m+v
\
{*„,+„}),
1 < u < v < m, and x', y' 6 X,
we
get
8(b',
x')
8(b",
y').
In
accordance with
8(b
+
t
,Xk)
=
b
m+t
,
k =
1,...,
5, and
b
m+t
{b
(
m+
t
, •••,
m+fK
t =
l,...,m,
let,
for any z e
{1,...,
r}, the zth
component
of
b
m+t
be
equal
to
8
2
(d{,
y), i = 1, 2,
with
D
z
= A
2
if and
only
if, for
every
k €
{1,...,
s},
the
zth
component
of
b
(K)
+t
is
equal
to a,.
We
allowed
5 = 1
(apart
from
cases
(la)-(3a),
which
we
shall study soon
after
the
general case). Thus,
in the
case
b' e
{b
(
^
+t
,...,
b(+
t
]
or b" e
[b
1
.
t
,...,
&£+,},
the
assumption {d
z
,
d'
z
]
=
{a
1
,
a
2
}
does
not
contradict
our
restrictions holding
for the
structure
on
fli,..., B
2m
c N.
There
is no
problem
if
(b
t
,
yi) =
8(b
t
, y
2
),
too.
(In
this case
we
may
get the
appropriate sets
by yi =
y
2
.)
Then, apart
from
cases
(la)-(3a),
we
obtained
b' b" for all
possible
cases
of b' 6 B
u
and
b" e B
v
.
Thus
the
required sets
B\,...,
B
2m
can be
constructed.
Now
suppose that
/C
contains
a
nonautonomous automaton,
i.e.,
for an A
3
=
(A
3
,
Xi,
83),
in
KC,
we
have
a € A
3
, x, y e X
3
with
3
(a,
x) ^
3
(a,
y).
Then
let yi, y
2
€ X be
given
with
yi y
2
and
suppose that
t
= A3 and
t
(y
1
)
= x,
t
(y
2
)
= y
hold
for
some
t €
{2,..., r}.Ifa
€ A
3
is the tth
component
of
every vector
&
r
,
t =
1,...,
m,
then
we get
(la).
