D?m?si P., Nehaniv C.L. Algebraic Theory of Automata Networks. An Introduction
Подождите немного. Документ загружается.


5.3.
The
Beauty
of
Letichevsky's
Criterion
1 61
Theorem 5.24.
Let n be a
positive
integer;
moreover,
let A be an
automaton
having
Letichevsky's
criterion
with
s-length
control
words.
Consider
the
digraph
D = (V, E)
with
V
=
{1,...,
ks},
E =
{(i,
i - 1
(modfks))
| i V} U
{(i,
i) | i
V]
U
{(1, .s),
(s,
ks)},
where
k =
[log
2
(n
+
1)1-
Every
n-state automaton
can be
simulated
isomorphically
by a
D-power
of
A
using
s-length
words
for the
simulation.
We
observe that
the
D-power
of A
considered
in the
previous result
is an
a
2
-v
2
l
-power
of
A.
Thus
we
receive
the
next theorem.
Theorem 5.25.
A
class
k
of
automata
is
complete
with
respect
to
homomorphic
or
iso-
morphic
simulations
under
the
a
2
-v
l
2
-product
of
automata
if
and
only
if
it is
complete
with
respect
to
homomorphic
representation
under
the
general
product.
We
will show later
a
generalization
of
this statement.
Now we
give
a
proof
of the
following
classical result.
Theorem 5.26.
A
class
K,
of
automata
is
complete
with
respect
to
homomorphic
represen-
tations
under
the
a
2
-product
if
(and
only
if)
it is
complete
with
respect
to
homomorphic
representations
under
the
general
product.
Therefore,
1C
has
these
properties
if
and
only
if
it
is
satisfies
Letichevsky's
criterion.
Proof.
It is
evident that every «2-product
is a
general product. Thus
the
necessity
of the first
part
of our
statement
is
trivial.
Proof
of the
necessity
of the
second
part. Assume that
K, is a
complete
class
of
automata
with respect
to
homomorphic representations under
the
general product. Then
we
can
also assume that every automaton
A can be
simulated homomorphically
by a
general
product
B
of
factors
in k. Let A be a
noncommutative strongly connected automaton. Then,
by
Proposition 2.76,
B
should
satisfy
Letichevsky's criterion. Using Proposition 2.71,
B
will have
a
factor
in K,
having
Letichevsky's
criterion.
(We
note that
an
automaton satisfies
the
Letichevsky criterion
if
either
one of its
homomorphic images
or one of its
subautomata
has
this property.
By
this
fact,
we can
also derive
the
second part
of the
necessity
of our
statement using Proposition 2.71.)
Proof
of
the
sufficiency
of
both
parts.
Let us
consider
the
following facts.
By
Proposition
5.17, there
exists
an
m-automaton
as a
single-factor product
of A.
Proposition 5.18 implies that
for
every counter
C,
there exists
a
loop power
of a
single-factor
product
of A
which homomorphically represents
C.
Having
Corollary 5.23,
the
two-state reset automaton
can be
simulated isomorphically
by
an
a
\
-power
of A
(having
s
factors).
Using Theorem 5.24, every automaton
can be
simulated isomorphically
by an a
2
-
powerof
A.
Therefore,
the
class
M. of
a
2
-powers
of A has all of the
properties
of k in
Theorem
3.28.
By
Proposition 2.51,
M. is a
complete class
of
automata with respect
to
homomorphic
representations under
the
cascade
product.
The
proof
is
complete.
We
note that,
by
Theorem 3.35,
we can
derive
a
simpler proof
of the
sufficiency.
In
addition, observe that reset automata have
the
properties
of the
automaton
A
given
in

1
62
Chapter
5.
Letichevsky's
Criterion
Theorem 2.68. Therefore,
we can
also derive
the
proof
of the
sufficiency
of
both parts
of
our
theorem
by
Theorem 2.68, Lemma 3.34,
and
Proposition 5.18.
By
Theorem 5.26
it is
proved that Letichevsky's criterion
can be
used
to
describe
those classes which
are
complete with respect
to
homomorphic representations under
the
a2-product.
On the
basis
of
this result,
the
next statement shows that
for i = 2, and
thus
for
every
i 2, the
a
i
,,-product
is
homomorphically
as
general
as the
Glu§kov product.
Theorem 5.27
(Esik-Horvath
characterization theorem).
For
every
automaton
A and
class
1C
of
automata,
A can be
represented
homomorphically
by an
a
2
-product
of
automata
from
1C
if
(and
only
if)
A can be
represented
homomorphically
by a
Gluskov
product
of
automata
from
k.
Proof.
If k
satisfies Letichevsky's criterion, then
we
apply Theorem 5.26.
If
1C
satisfies
the
semi-Letichevsky criterion, then
we
consider Corollary 4.15.
It
remains
to
study
the
case
when
1C
does
not
have Letichevsky's criterion. Then
we
consider Theorem 4.48.
The
proof
is
complete.
Of
course,
the
Letichevsky decomposition theorem (Theorem 2.69)
can be
derived
from
the
above result.
We
remark
it is now
easy
to see
that
a
direct proof
of the
Letichevsky
decomposition theorem
can be
generated
in the
following way.
Proof
of
Letichevsky decomposition theorem.
The
necessity
of
Letichevsky's criterion
directly comes
from
Proposition 2.71.
As to
sufficiency,
we
observe that reset automata
have
the
properties
of the
automaton
A
given
in
Gluskov's theorem (Theorem 2.68). There-
fore,
we can
derive
the
direct proof
of the
sufficiency
by
Theorem 2.68, Lemma 3.34,
and
Proposition 5.18.
5.4
Bibliographical
Remarks
Section
5.1. Lemmas
5.5 and 5.7 and
Theorem
5.9 are
given
in
Domosi
and
Esik [2002].
All
other results
in
this section were developed
in
Domosi
and
Esik [2001].
Section
5.2.
The
results
of
this section
are
presented
in
Domosi
and
Nehaniv
[2000].
Section53.
Lemmas 5.19
and
5.20
are
new. Theorem5.21
was
proved
by P.
Domosi [1994].
Proposition 5.22, Corollary 5.23,
and
Theorem 5.24
are new
observations. Theorem 5.25
is
a
strengthened version
of the
main result
in
Domosi
[1996].
Theorem 5.26
is a
well-known
result
of Z.
Esik [1985].
It
highly improves
the
main result
of P.
Domosi [1983].
The
Esik-
Horvath
theorem (Theorem 5.27), i.e.,
the
fact
that
the
a
2
-product
is
homomorphically
equivalent
to the
general product,
was
proved
by
Esik
and Gy.
Horvath [1983].
A
nice
explanation
of
this statement
and
Theorem 5.26
is
given
by
Gecseg
[1986].

Chapter
6
Primitive
Products
and
Temporal
Products
In
this section,
one
of
our
fundamental concepts
is
that
of the
primitive
product.
Why is
it
important?
A
primitive
product
is a
composition
of
a finite
sequence
of finite
automata
such that feedback
is
limited
to no
further than
the
previous factor. Furthermore,
the
input
to
each factor depends
only
on the
global input
to the
system
and the
states
of
at
most three
factors (including
the
factor
itself).
Conversely,
the
state
of
a
factor
may
directly
influence
only
at
most three factors (including
the
factor
itself).
Thus,
the
number
of the
possible
local links
is
also strongly restricted.
We
show that
the
primitive
product
is one of the
simplest
type
of
products that preserve
the
completeness properties
of
the
general product.
The
primitive
product
is
general
in the
sense that exactly those classes
are
complete
with
respect
to
homomorphic representation under
the
primitive
product which
are
complete with
respect
to
homomorphic representation under
the
general product (i.e., with unrestricted
networking).
On the
other hand,
we
will
see
that
the
primitive
product
is a
special
type
of
the
a
o
1-v
l
2
'product
such that
it has a
strong restriction
on the
permitted number
of
local
links.
By our
results
in
Chapters
3, 4, and 5, we can
establish that
an
a
i
-Vj-product
or
an
a
i
-v
l
k
-product with
i<2 or j 2 or k < 2
cannot preserve
the
generality
in the
considered
sense.
Therefore,
we
would lose
the
generality
of the
primitive
product
if
we
tried
to
give
further restrictions
on the
structure
of
permitted links. Additional conditions
guarantee
a
strongplanarity property
(outerplanarity),
which
is
desirable
in the
engineering
of
sequential circuits.
Also
studied
in
this chapter
is the
temporal
product
This
is a
model
for
multichannel
automata networks, where
the
network
may
cyclically change
its
internal structure during
its
work
on
each channel.
We
will
see
that this concept
may be
much stronger with respect
to
homomorphic
or
isomorphic representation than
the
general product.
Therefore,
the
study
of
automata networks which
can
modify
their inner structure during their work
may
prove
very
important from
the
point
of
view
of
many applications.
1 63
164
Chapter
6.
Primitive
Products
and
Temporal
Products
6.1
Primitive Products
Take
the
above considered general product
A = A
\
x • • • x
A
n
(X,
\
, • • •,
n
) and its
underlying
graph
D = (V, E). For any t V,
denote
by
i(t)
and
o(t)
the
sets
of
incoming
and
outgoing edges
of t,
respectively,
and
assume that
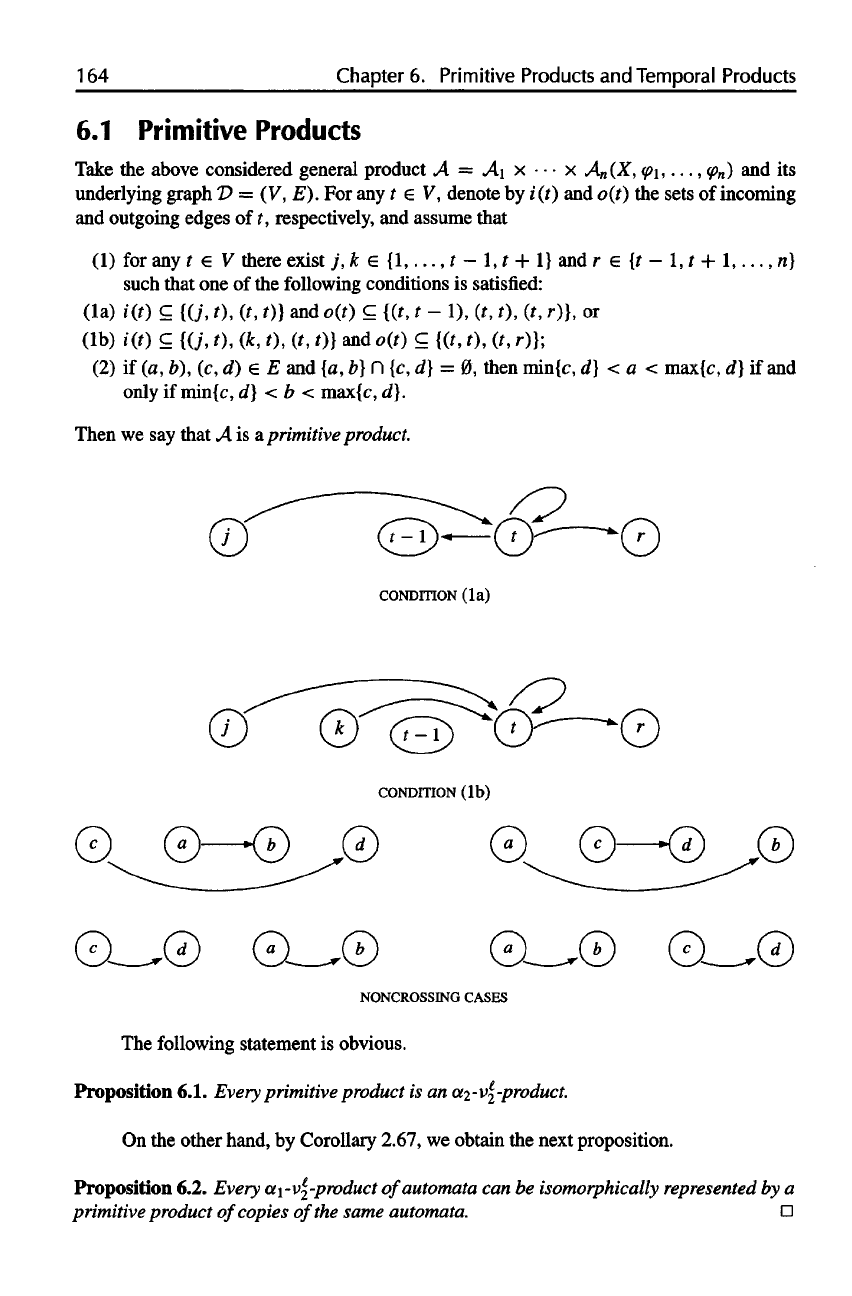
(1)
for any t V
there exist
7, k
{1,...,
t - 1, t + 1} and r € {t - 1, t +
1,...,
n]
such
that
one of the
following conditions
is
satisfied:
and
and
if
and
then
min
max{c,
d} if and
only
if
mini
max{
Then
we say
that
A is a
primitive product.
The
following statement
is
obvious.
Proposition
6.1.
Every
primitive product
is an
a
2
-V
2
-product.
On
the
other hand,
by
Corollary 2.67,
we
obtain
the
next proposition.
Proposition
6.2.
Every
a
1
-v
l
2
-product
of
automata
can be
isomorphically
represented
by a
primitive
product
of
copies
of
the
same automata.

6.1. Primitive
Products
165
For any
class
/C of
automata,
let us
consider
the
class P(k)
of
primitive products
having
factors
from 1C. It is
easy
to see
that
P(P(k))
P(k) does
not
hold
in
general.
However,
we
have
the
following.
Proposition
6.3.
Let M = M \ x • • • x
M
n
+i(X,
» • • •.
+i).
n I, be a
product
of
primitive
products
M
i
=
MI,\
x • • • x
M
I,Ji
,
(X,•,
i,...,
ij,),
ji 2, i =
1,...,
n + l,
having
the
following
properties,
1
,...,
n
may
really
depend
only
on
their
input
variables.
Moreover,
.i,...,
j-i,
i =
,...,n,
really
do not
depend
on
their
last
(ji)th-state
variables,
and,
if
some
n+1,k
(k
=
1••>
j
n+1
)
really
depends
on its
input
variable,
then
it may
additionally
depend
only
on its kth
state variable
and at
most
one
other state
variable,
and,
simultaneously,
there
exists
at
most
one
n+1k,'
( ' = 1
•••jn+1)
jn+1)
with
k k
f
depending
on its kth
state variable. Furthermore,
the
input
set
of
M
n
+i
is
X
n+
i
=
MI1
}
x
M
2
,J
2
x • • • x
M
n
j
n
,
where
Miji.
,i =
1,...,
n,
denotes
the
state
set
of
the
last
factor
of
the
product
MI, and
each
n
+1,k
(k =
I,...,
j
n
+1)
may
depend
at
most
on one
component
of
X
n+1
,
and, moreover n+1.
and
+1,k+'
do not
depend
on the
same
component
of
X
n+l
fork
k' (k, k' =
1,...,
7n+i).
If
n+i
has
the
form
n+
i(mi,
...,m
n
,
m
n
+1,
x) = (m1
,...,
m
n
j
n
)
X
n
+\,
where
m,
is the
state
of
Mi and
m,
>;(
the
state
of
Mi's last
factor,
then
M is
isomorphic
to a
primitive
product
of
M
i
j, i =
1,...,
n + 1, j =
1,...,
ji.
Proof.
Let P be an
arbitrary permutation over {1,..., n}.
34
Considering
the
short notation
N
e
=
M
e
,\
x • • • x
Mt,j
t
(t =
1,...,
n + 1), by
Proposition 2.50,
we can
construct
the
product
with
u — ji + • • • +
jn+i
such that
M! is
isomorphic
to M..
Denote
n+
i
.s
1
.
• • •
n+i,s
r
with
s\ < • - • < s
r
to be all
feedback
functions
of the
product
M
n+
i
depending
on at
least
one
component
of the
input
set
X
n+
\
= M
1,j1
x
M
2
j
2
x • • • x
M
n
j
n
.
From
our
assumptions
it
follows that
r < n.
Suppose that
for
every
l
{1,...,
r], P(n — l + l) = t,
whenever
n
+1,
St
depends
on the tth
component
of
X
n+
\. Clearly, then
M'
forms
a
primitive product
of
the
Mij,
i =
1,...,
n + 1, ; =
1,...,
ji.
Lemma 6.4.
Let D = (V, E) be the
underlying
graph
of
a
primitive product
of
automata.
Then
D has the
ordered
cycle
property.
Proof.
The
nodes
of D are
already integers,
so we
consider
D
under
its
natural labeling.
Claim.
Take
any
pair
of
undirected paths i
\
...
i
m
,
j\...
j
n
consisting
of
nodes
in D,
with
ji < ii < j
n
and
suppose either
i
m
< ji or j
n
< i
m
.
Then
the
paths contain
a
common
point.
Proof
of
Claim.
Assume that
the
claim
is
false; then there
is a
minimal counterexample,
with
all
nodes distinct
and n + m
least.
Consider
i
m
-\:
if
i
m
-\
< j\ or j
n
<
i
m
-\, then
the
path i\... i
m
-\ would yield
smaller counterexample unless
m = 2. If on the
other hand
71 <
i
m
-\
< j
n
,
then
i
m
-ii
m
34
In
other
words,
let P be a
bijective mapping
of
{1,...,
n}
onto itself.

1 66
Chapter
6.
Primitive
Products
and
Temporal
Products
yields
a
shorter counterexample unless
m = 2. So m = 2 for a
minimal counterexample.
Now,
consider
the
path
j
\
• • • j
n
. If i
2
< j
1
then
i
2
< 71 < i'i < j
n
. In
this case,
by
(2),
i
2
< j
2
< i
1
must
hold,
and
thus,
72 • • • j
n
yields
a
shorter counterexample until
n = 2. If
y
n
< i
2,
then
ji < i\ < j
n
< i
2
-
Then,
by
(2),
i\ <
j
n
-\
< i
2
must hold,
but in
this case
ji • • •
jn-i yields
a
shorter counterexample.
We
have established that
n = m = 2 in any
least counterexample. Thus,
i
2
< ji <
i
1
< J
2
or ji < i\ < J2 < i
2
now by
condition
(2) of the
definition
of
primitive product,
since
j\ =
minjji,
72}
< i\ <
max{j\,
72}
= 72, we
have
j\ < i
2
< 72, a
contradiction.
Therefore,
no
least counterexample
can
exist. This establishes
the
claim.
Now
let c\
denote
the
least
node
in the
real cycle.
It is
connected
by
edges
in the
real
cycle
to two
other nodes.
Now
these
two
nodes
and c\ are
pairwise distinct.
Let c
2
denote
the
lesser
of the two and let c
k
denote
the
greater.
We
have
c\ < c
2
< c
k
.
Proceeding
around
the
real cycle
in the
direction
from
c\ to c
2
denote
the
nodes
c
3
, c
4
,
etc., until
we
reach
c
k
. We
assert that
C
k
is the
greatest node
in the
real cycle;
if
not,
let c
i
be the
node
with
least
i
such that
c, > c
k
.
Note that
i 3. By
leastness
of i,
ci_1
< c
k
, and so it
must
be
that
c
i
, > C
k
>
c
i
,-1
> c\, but
then
the
path
C
k
C\
and the
path
c,C
i
_i
would comprise
a
counterexample
to the
claim. Hence,
c
k
must indeed
be the
greatest node.
Furthermore,
it
must
be
true
for
each
i =
1,...,
k
—
1
that c
i+
\
> c
i
: If
not, take
an
i
such that c
i+
\
< c
i
.
Then
we
have
i
{\,k
—
1], and so c
\
<
c
i+
\
< c,
<c
k
.
But
then
c
r+1
...
C
k
is a
path disjoint
from
the
path c
\
... c
t
•,
and we
would have contradiction
to
the
claim.
We
have established that
c\ < c
2
< • • • < c
k
for the
nodes
c
\
,
c
2
,...,
c
k
met in
sequence traced
as we go
around
the
cycle starting
in the
direction
from
c\ to c
2.
Corollary
6.5.
The
underlying
graph
of
any
primitive product
is an
outerplanar
graph.
Proof.
A
graph
is
outerplanar
if and
only
if it
contains
no
subdivision
of K
4
, the
complete
graph
on
four
nodes,
and no
subdivision
of the
complete bipartite graph K
2,3
- However,
such
a
subdivision cannot have
the
ordered cycle property established
in the
lemma, since
if
it
did, then
by
restriction
the
property would hold also
for K
4
or
£2,3-
But it is
easy
to
check that
K
4
and
k
2,3
do not
have this property.
Remark
1. As we see
from
the
proofs
of
Lemma
6.4 and
Corollary
6.5,
every
product
of
automata whose
underlying
graph
satisfies
condition
(2) in the
definition
of
primitive
product
has the
ordered
cycle
property
and an
outerplanar
underlying
graph.
Remark
2.
From
the
engineering point
of
view
of
circuit wiring,
outerplanarity
is an
extremely
desirable
property,
since
a
circuit whose
components
and
wires
comprise
the
nodes
and
edges
of
an
outerplanar
graph
may be
realized
on
aflat
surface.
Moreover,
new
wires
can be run
from
a
point
outside
the
circuit
to any or all
nodes
of
the
circuit
without
crossing
each other
or any
of
the
existing
wires.
6.2
Primitive
Products
and
Letichevsky's
Criterion
We
constructively show that
if A is a finite
automaton
satisfying
Letichevsky's criterion,
then
any finite
automaton
can be
homomorphically represented
by
(i.e.,
is a
homomorphic

6.2.
Primitive
Products
and
Letichevsky's
Criterion
167
image
of a
subautomaton
of or,
equivalently,
is a
letter-to-letter (length-preserving) divisor
of)
a
primitive product
of
copies
of A.
Take
two
alphabets
X and 7. Let n = is (l > 1) be a fixed
integer
and
consider
a
mapping
: X
n
Y
n
having
the
property
{
(/?)
| p X
n
} {w | w {u,
v}
£
}
for
some
fixed
words
u. v € Y
s
. We
shall denote
the
reverse
of ( ) bv
(p}.
Set
Define
to
be the
automaton,
where
d is a
positive integer,
R
r
,H,d
=
{(k,
p,q)
€
(1,...,n}
x X* x Y
+
\
k+\q\
=n+d,
\p\ (0, k}, is a
prefix
of a
word
in H
(pp'
H for
somep' X*),and,
furthermore,
q —
q'q", where
q'' is a
suffix
of u or v and q" {u,
v}*}, and,
for
arbitrary
(k,
p, yq) € R
,
H
,d
(y { , v
t
\ t =
1,...,
s}) and x X,
To
simplify
the
proof
of the
next result,
we
introduce some auxiliary notions.
Let
A = (A, X
A
, 8
A
) be an
automaton satisfying Letichevsky's criterion,
and let
u
\
...
u
s
, v\
... v
s
be any
pair
of its
control words.
For any
w\...w
s
with
w
t
{u
t
,
v
t
} (t =
1,...,
s)
we
shall
use the
short notation
w.
Consider
a
word
a
\...
a
n
A
+
and an
integer
k (= 1,
...,
n). We
will denote
by
c(a
\
...a
n
,
k) the (k +
l)th
cyclic permutation
of
a
\...
a
n
.
In
more detail,
let
In
addition,
for any
pair
t, k
with
t
let
and for any
integer
r,
denote
by
the
reverse
of
c(a\...
a
n
, r).
Let
M
be an
automaton with
moreover,
let B
be a
subautomaton
of M.
having
a
homomorphism
onto
such
that
implies
.
Then
we say
that
M
y-represents
R
,H,d
(with respect
to
We
have
the
following.
Lemma 6.6.
Let A = (A, X
A
, 8
A
) be an
automaton
satisfying
Letichevsky's
criterion
and
let
u
\...
u
s
,
v
\
...
v
s
be
any
pair
of
its
control
words.
Consider
an
alphabet
X, a
multiple
n
of
s
with
n = is, l > 1, a
word
r X
n
, and a
mapping
: X
n
A
n
having
the
property
(p)
€ {u,
v}+l
for
each
p X
n
.
Then
there
exists
a
primitive power
M.
of
A
such that
R
,M,i
is
y-represented
by M. In
addition,
apart
from
the
feedback
functions
for the
last
factor,
the
feedback
functions
of
the
factors
of
M.
really
do not
depend
on
their last state
variable.
1
68
Chapter
6.
Primitive
Products
and
Temporal Products
Proof.
For the
proof
of our
statement,
first we are
going
to
define
a
product
N =
having
the
following structure:
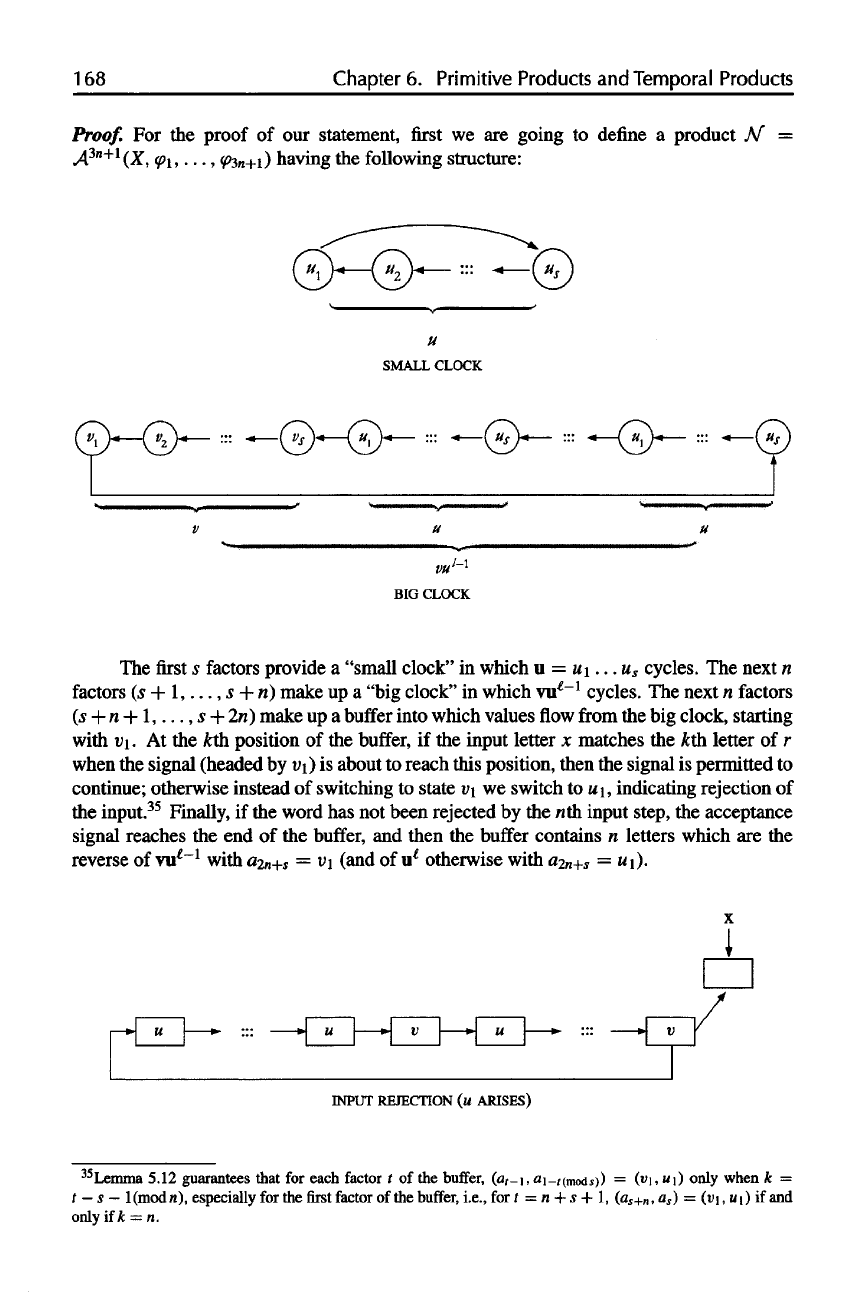
The
first s
factors provide
a
"small
clock"
in
which
u =
u\...
u
s
cycles.
The
next
n
factors
(s +
1,...,
s + n)
make
up a
"big
clock"
in
which
vul
-1
cycles.
The
next
n
factors
(.s+n
+
l,...,.s
+ 2n)
make
up a
buffer
into which values
flow
from
the big
clock, starting
with
v
1
. At the kth
position
of the
buffer,
if the
input letter
x
matches
the kth
letter
of r
when
the
signal (headed
by v
\
) is
about
to
reach this position, then
the
signal
is
permitted
to
continue; otherwise instead
of
switching
to
state
v\ we
switch
to u
I
,
indicating rejection
of
the
input.
35
Finally,
if the
word
has not
been rejected
by the nth
input step,
the
acceptance
signal reaches
the end of the
buffer,
and
then
the
buffer
contains
n
letters which
are the
reverse
of
vu
l-1
with
a
2n+s
= v\
(and
of u
£
otherwise with
a
2n+s
=
u
1
).
35
Lemma
5.12
guarantees
that
for
each
factor
t of the
buffer,
(ar-1,«i-r(modj))
=
(v
\
,
u
1
)
only when
k =
t
—
s
—
l(modn),
especially
for the first
factor
of the
buffer,
i.e.,
for t = n + s + 1,
(a
s+n
,
a
s
) =
(v
\
,
u
1
) if and
only
if k = n.

6.2.
Primitive
Products
and
Letichevsky's
Criterion
1 69
In the
next step,
the
buffer
cycle starts again, while
in the
last
n — s + 1
factors
(2n
+ s +
1,...,
3n + 1), the
coded word
(r)
begins
to
take
form
if the
signal
has
arrived.
Now
(r) =
w
1
...
w
l
,
where each
w
j
{u, v}. For
each
j =
1,...,
I
with
w
l_+1
= v
in
this step
v1
simultaneously enters
factor
2n + js + 1,
while
for the j
with
w
l
-
j+1
= u
and
u
1
enters
this factor.
It is
important
to
observe
that
(r) can be
fully
recovered
from
the
states
of
these
t
nodes
at
this time,
as
follows
from
u
\
v
\
and the
form
of (r) {u,
v}
£
.
In the
next
s — 1
steps,
the
letters
in
these
factors
shift
to the
next highest factor
and the
respective letters
of u and v flow in.
Thus, this last part will contain
(r)
except
for its first
.s
—
1
letters,
as
a2n+s+1•
• •,
a
3n+1
after
s
steps. Observe that
the
letters
of (r)
appear
as
n
successive states
a
3n+\
of
A
3nn+1
,
which
is the
last
factor.
If
the
signal
did not
arrive,
the
above transition rules imply that
u
1
will
be in the
buffer
after
n
input letters
and
will then
flow
through
and out of the
next part.
We
will
use the
fact
that, except
for the
last
(3n +
l)th
factor,
the
feedback
function
(p
t
of the tth
does
not
depend
on its
last state
factor
a
3n+1
•
As to the
mapping onto
R
T
,{
r
},d,
take
a
triplet
(k, p, yq)
R,{
r
},\
(y
{u
t
,
v
t
\
t
=
1,...,*}).
We
represent this triplet
(k, p, yq) by an
appropriate state
b
=
c(u,
k)c(vu
l
~
l
,
k)c(zu
l
~
l
,
k -
\)e\...
e
n
-
s+1
of N. The
number
k is
represented
by
the
value c(vu
l
~
l
,
k) and
c(zu
l
~
l
,
k — 1), z =
z
1
...
z
s
represents
p
with
z
i
,
{u
i
, v
i
,},
i
=
1,...,
s.
Namely,
if
z\ = u
1
,
thenp
= is
assumed,
and
if
z\ = z
\
,
then
p is
understood
as
the
k:-length
prefix
of r. In
other words,
z\ = v
\
means
r = pp' for
some
p' X*
(with
\p\
= k). And z\ =
MI
means
p = .
Setting y
1
...
y
n
{u,
v}
£
, assume
Then
k and the
mirror image
of e\
obvious
considering
the
structure
of
l > 2,
then
the
mirror image
of e\
i
represents
If
then
this
is
representing
(Observe that
k and
unambiguously
determine
moreover,
for anv
unambiguously determines
We
have
similar
consequences
for
and
l = 2. The
motivation
for
this representation should
be
clear
from
the
explanation
of the
buffer
cycle discussed above.
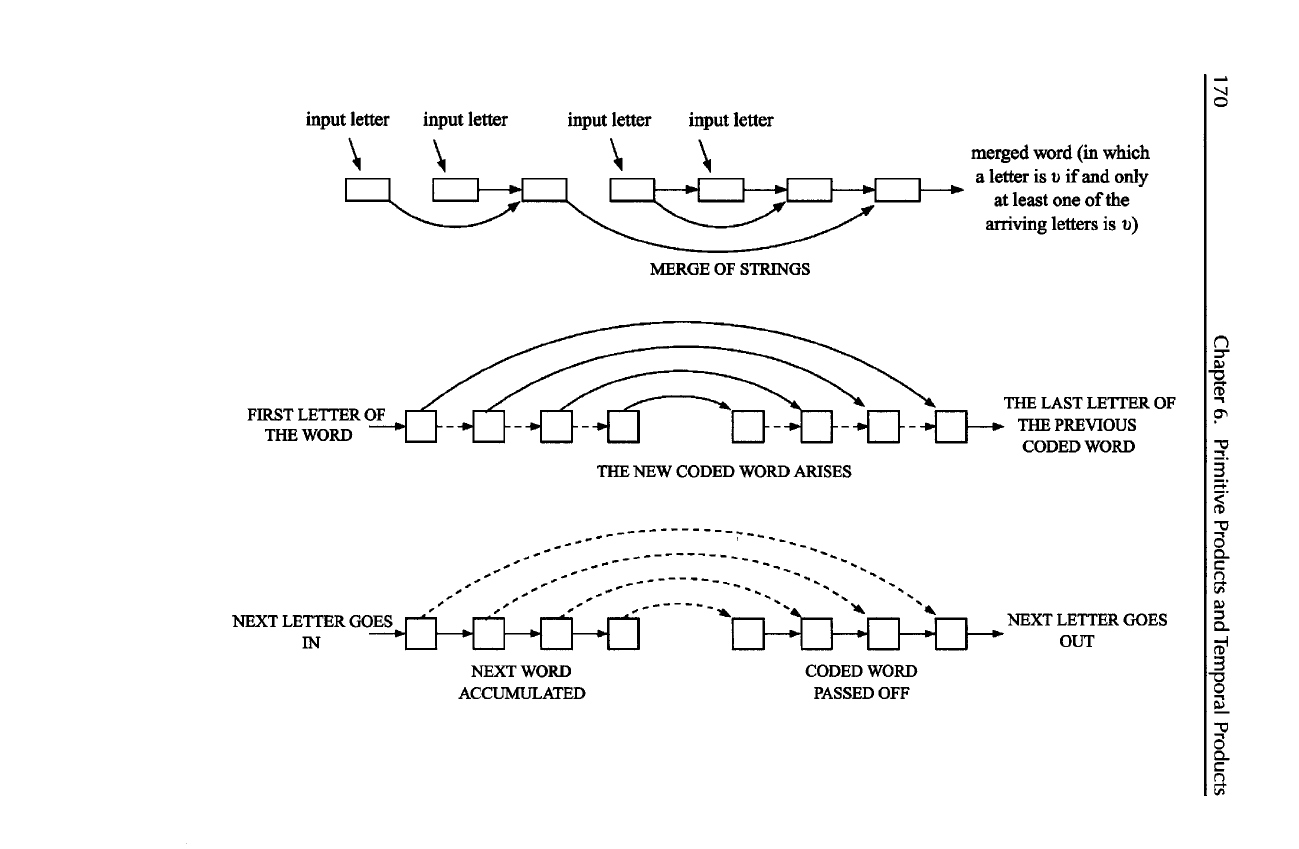
input
letter
input
letter
input
letter
input
letter
merged word
(in
which
a
letter
is if and
only
at
least
one of the
arriving letters
is )
MERGE
OF
STRINGS
FIRST
LETTER
OF
THE
WORD
THE
LAST LETTER
OF
THE
PREVIOUS
CODED WORD
THE NEW
CODED WORD ARISES
NEXT LETTER GOES
IN
NEXT LETTER GOES
OUT
NEXT
WORD
ACCUMULATED
CODED
WORD
PASSED
OFF
