D?m?si P., Nehaniv C.L. Algebraic Theory of Automata Networks. An Introduction
Подождите немного. Документ загружается.


7.1 .
State-Homogeneous Networks
and
Some
Technical
Lemmas
201
Then
for
arbitrary,
pairwise
distinct
i, j, k e [I, . . . , n} we get
Proof.
Although
it is
simple
and
elementary,
we
give
a
detailed
proof
of our
statement
to
make
the
matter more understandable.
In
particular,
we
prove
our
statement
by the
following
computations:
202
Chapter
7.
Finite State-Homogeneous
and
Asynchronous
Automata Networks
Lemma 7.2. Given
a finite
group
G and a
pair
of
relatively
prime
integers
m, n
with
\ <m < n, let us
define
for
every
t e
{1,...,
n}, the
transformations
T
{
: G
n
—>
G",
7Ti
(k)
: G
n
-+ G", k = 1, 2,
3,4,
as
follows:
Then
for any fixed
Proof.
For
every
Thus
we
shall show onl)
clear that
by the
simple
fact
that every permutation
is a
composite
of
transpositions and,
moreover, transformations
can be
generated
by
permutations
and
elementary collapsings,
using
the
notation
in
Lemma 7.1,
we
obtain
On
the
other hand,
{{r
(0)
,
if | k =
Thus,
it is
enough
to
prove that
for
every
1,2,3,4,1
=
!,...,«}).
Using
= 0,
1,...,
by an
inductive application
of
Lemma 7.1,
We
have
^•_
m
_i(
mo
dn)
)I
-+./m-l
(modn)
{l,...,n,},y=0,l...).
Therefore, because
m and n are
relatively prime,
we
receive
Moreover,
we
also have
F^
(luui
applying Lemma
7.1
again,
we
obtain
L
i, j 6
{1,...,
n}, and
thus, having
F^ c
the
proof
is
complete.
We
shall
use the
following lemma.
Hence,
|K
=
1,2,3,4}).
k
=
1,2,3,4).
L,2,3,4,l
= 1,
k
=
1,2,3,4,l
= I,

7.1
.
State-Homogeneous Networks
and
Some
Technical
Lemmas
203
Lemma
7.3.
Given
a
positive
integer
n, let G — {g}
denote
a finite
nontrivial
cyclic
group
with
a
generator
g € G.
There
exists
an
arrangement
a
1
, . . . , a
m
(m =
|G|
n
)
of
the
elements
in the nth
direct
power
G
n
ofG
such
that
for
every
i = 1, . . . , m — 1
there
is
a j e [I, . . . , n}
with a,-
+1
€
{(gi,
. . . ,
g,-_i,
g/g
-1
,
gj+i,
. . . ,
g,,),
(gi,
. . . ,
g
;
-i,
g;g,
g
j+
i,
...,
g
n
)}, whenever
a
i
,
=
(gi,
. . . , g
n
) (e
G").
Proof.
If n = 1 ,
then
our
statement
is
trivial.
Now let us
suppose that
our
statement holds
for
n
> 1 and let ai, . . . , a
m
be a
suitable arrangement
of G".
Then
(g,
a\),
(g,
02),
. . . , (g,
a
m
)>
(g
2
,
flm),
(g
2
,
flm-i), • • • ,
(g
2
,
fli),
(g
3
,
fli),
(g
3
,
a
2
),
• • • ,
(g
3
, a
m
),
• • • ,
(*
|G|
,
flr),
where
f
= 1
(resp.,f
=
m)if
|G| is
even (resp., odd)
is a
suitable arrangement
of
the
(n+l)th
direct
power
G
n+1
of G,
where (g
K
, a,-)
=
(g
k
,
g
1
. . . ,
g
n
), whenever,
a,- =
(gi,
. . . , g
n
)
(fc
=
1,
. . . ,
|G|,
i =
l,...,
m). The
result
now
follows
by
induction.
Given
a
nonvoid
set Y, a
positive integer
w, let 7y
denote
the
full
transformation
semigroup
of all
functions
from
Y to Y. In
addition,
for
every subset
H 7y , let
(H
)
denote
the
subsemigroup
of 7y
generated
by H.
Moreover,
for any finite set X
with
|X| > 1 and
positive
integer
n > 1 ,
denote
by
Tx,
n
the
subsemigroup
of
all
transformations
of 7x
having
theformF(jci,...,j:
n
)
=
(A:
f
(i),...jr
t
(
n
)),
(*!,...,*„)
€X
n
,t
\ {1,
...,n}
-»
{!,...,«},
and
let
where
/ : X
2
-» X, i, 7 € (1, . . . , n},
(jci,
. . . ,
jc
n
)
e
X
n
}.
(It is
understood that
the
case
i = j is
allowed
in the
above definition
of
FX»
.)
Define
the
elementary
collapsing
tj,
k
: {1, . . . , n} -+ {1, . . . , n} for 1 < j k < n,
Moreover,
as
usual
we say
that
U
jk
: {1,
...,n}->
{1,...,
n} for 1 < j k < n is a
transposition
if
where
(x\,,..,
*„) e X
n
similarly
as in the
previous lemma.
In the
following,
we
shall
identify
X in a fixed but
arbitrary
way
with
the
group
of
residue classes
of
integers modulo
q =
\X\.
Now
we are
ready
to
prove
the
following
key
lemma.
Lemma
7.4.
For any fixed t e
{!,...,n},
Tx
n
is
generated
by the
union
of
{{r<°>,
Te
(k)
| k =
1,...,4}}
and the set
of
all
Junctions
F : X
n
-> X
n
having
the
form
F(XI,
...,*„)
=
(*i,...,
*/_i,
f(x
it
...,
x
n
),
^+1,...,
*„),
/ : X
n
-» X,
w/iere
X\, . . . , X
n
€ X.
Finally,
define
u
i,j
: X
n
-» X
n
by

204
Chapter
7.
Finite State-Homogeneous
and
Asynchronous
Automata Networks
Proof.
We can
take
out of
consideration
the
trivial case
\X\ = 1.
Thus
we
assume
\X\ > 1.
It
is
clear that without
loss
of
generality
we may
suppose
I = 1. On the
other
hand, using Lemma
7.2,
{£/,,,
| i,j e
{!,...,«}}
C
({T
(0
\T^
\ k =
1,...,4).
Thus
it is
enough
to
prove that
the
union
of
{U
f
j
\ i, j e
{!,...,«}}
and the set of
all
functions
F : X
n
-* X"
having
the
form
F(x
1
,
...,*„)
=
(f(x\,
. . . ,
*„),
x
2
, . . . ,
x
n
)
generates
7x«
.
For
every pair
i e {1, . . . , n}, f : X
n
->• X,
define
the
function F
iif
: X
n
-> X
n
with
F
it
f(xi,
...,*„)
=
(xi,...,Xi-i,f(xi,...,x
n
),x
i+
i,...,x
n
),
(XI,...,X
H
e X).
Thus,
by
letting
/' = Uij o /, we
have FJ,f
= U
{
j o
F
it
f
o
U
f
j.
So for
every pair
i
€
{!,...,«},
/ :
X
n
'->
X,
F
itf
€
(T
x
,
n
U{F
: X"' -» X
n
\
F(*i,
...,*„)
=
(f(xi,
...,
x
n
),
x
2
, *
3
,
...,*„),/:
X
n
^ X, *i,
...,*„
e
X}).
Let us
identify
X
with
a
nontrivial
finite
cyclic group with generating element
g
e X.
Thus
we
also have that
for any c\, . . . , c
n
e X,
F
(1)
e>J;
(
C
,,...
>Cn
),
F
(2)
€i;i(cli
...
;Cn)
€
(Tx,
n
V{F
: X
n
^ X
n
\
F(JCI,...,x
n
)
=
(/(jti,
. . .
,x
n
),x
2,X3
,'.
. .
,x
n
),
/ :
X»"
-»
X,
x =
(jci,
. . . ,
jc
n
)
€
X"}), whenever
€ e {1,
-1),
otherwise,
where
x =
(x\,...,
x
n
) e X
n
. On the
other hand,
by
Lemma
7.3,
there exists
an
arrange-
ment
GI,
...,
a
m
of X
n
such that
for
every
k =
1,...,
m — 1, ;?* e
{^
(1)
e
7 (ci c«) I
6
6
{-1,1},
j e
{!,...,
n},
Cl
,...,c
n
€ X}, tk €
{F(\
;
.,
(cl)
...,
Cn)
| 6 e
{-1,1},'7
e
{!,...,
n},
ci,...,
c
n
€ X},
where
But
then
p\,...,
p
m
-\
is a set of
transpositions such that
{p\,...,
p
m
~i} generates
all
permutations over
X
n
.
Furthermore,
t1,...,
t
m
-\
is a set of
elementary collapsings over
X
n
.
Thus
by the
well-known
fact
that
for
every
j =
1,...,
m — 1,
(p\,..., p
m
-\,
tj}
generates
all
transformations over
X
n
, the
proof
is
complete.
D
Lemma
7.5.
T
x
,
n
£
(IV).

7.1
.
State-Homogeneous
Networks
and
Some
Technical
Lemmas
205
Proof.
Using Lemma
7.1,
we
have that
for any
pair
i ^ j
{1,...,«},
Ujj e
(r
x
«).
On the
other hand,
[F$ \ i, j € {
,...,«}}
C
(IV)
holds
by
definition.
Re-
call that
Uij
transposes
the
elements
in the ith and yth
positions
and
that
F
(3)
-
replaces
the
yth
entry
by the
ith.
Therefore,
by the
simple
fact
that every permutation
can be
composed
as
a
product
of
transpositions
and,
moreover, transformations
can be
generated
by
permu-
tations
and
elementary collapsings,
we
obtain
the
inclusion
of our
statement. Finally,
it is
trivial that
FX«
\
Tx,
n
is
nonvoid.
D
Lemma
7.6.
Given
an
alphabet
X and a
positive
integer
n >
We
have
F^
<-,_,)
e
<r
x
«).
Proof.
If n = 2,
then
our
statement holds
by
definition. Otherwise,
n > 2 and for
every
b
e X,
define
where
For
every
where.
where
x =
(x
1
,...,
x
n
) e
X").
It is
clear that
F ) = F . On the
other hand,
for
every
i
e
{2,...,
n - 1},
Fta.,,...,^,)
=
C/f-Ln-i
o F£> o
tf,-_i,
B
_i
o
F
(c
.
Cn
_
0
. Simultaneously,
we
have
by
definition that
F
(0)
€ r
x
»
holds
for
every
z €
{2,...,
n — 1}.
Moreover,
by
Lemma
7.5 we
have
i,j e (IV
)•
Thus
we get our
result
by
induction.
Lemma
7.7.
Given
an
alphabet
X and a
positive
integer
n
_i)
is
allowed)
and let
Then
we
have
Fl
Proof.
We
have
c € X
arbitrary with
c d, and set
,
and

206
Chapter
7.
Finite
State-Homogeneous
and
Asynchronous
Automata Networks
where
jc =
(*i,...,
JC
M
)
e X
n
;
moreover,
define
F(
Cli
...
iC(1
_,)
as in
Lemma
7.6.
In
addition,
let
and
for
every
a e X, let
((x
1
,
...,x
n
)
€
X").
It is
clear that F
c
(3)
,
F
d
F
(5)
,
F
a
(6)
€
Y
X
n.
Next
we
show that
F
(cL.,c
n
-,),(d,
4,-,)
€
<
r
x">-
Indeed,
by an
easy computation
we get F^.
Cn 0
(t/]
^_
i}
=
fy,....A-,) o F®, o
f/
n
_2,
n
-i
o
F
c
^
2
o
f/
n
_
3>n
-i
o • • • o
U
2
,
n
-i
o
F^
6
>
o
f/
lin
_,
o F«> o
t/i,
n
_i
o
^2,«-i
o • • • o
U
n
_
2
,n-i-
On the
other hand,
by
Lemma
7.7 we
have
Utj e
(fx").
But
then
C.,c,-,),(«
*-,)
=
f
c
<3>
o
F^.....
c
..,,,
tf
„._,,
o Ff
implies
fg»...
A
.
l)>w
„._,,
€
(Tx"}-
It
remains
to
prove that
F,
(1)
. ^ /j ^ ^ e
(Fy
n
).
This connection,
com-
pleting
the
proof, comes
from
Let
JF
xn
-i
x{rf}
be the
semigroup
of
functions
{F e 7x« I
F(^i,...,
*„) e X
n l
x
{rf},
jci,...,
x
n
e X,
where
F is
really independent
of
x
n
}.
By the
above statement
we get the
following
result.
Lemma
7.8. Fx
n-1
-'xw
£
(IV).
Proof.
For
every pair
(ci,...,
c
n
_i),
(rfi,...
,d
n
-\)
e
X
n-1
,
let us
define
the
mappings
F^
Cn i} (di dn i}
, F^
Cn i} (d[ dn i}
as in
Lemma
7.7.
Observe that
F(c?
C
B
_!)
(dj
4_i)
acts
as a
transposition
in the
permutation group over
the set
X
n-1
x
{d},
while
Ffa
Cn
_
{
)
(fH
d
n
-\)
acts
as an
elementary collapsing
in the
transformation semigroup
over
the set
X
n-1
x
{d}.
By
Lemma
7.7 we
obtain that
all of
these transpositions
and el-
ementary collapsings
are in
{Fx«>.
It is
well known that
the set of all
transpositions
and
elementary collapsings
on a set
generates
all
mappings
on
that
set,
so any map
taking
X""
1
x {d} to
itself
may be
written
as the
restriction
to
X""
1
x {d} of a
composite
of the
above functions.
A
moment's reflections shows that
the set of all
these
F^
c
, ,
d d
.,
F(CI
.
c
n
-i)
(di
d
n
_
1
)infactgeneratesallof^
:
x»-
1
x{d}.sinceafunctioninthelatterisuniquely
determined
by its
behavior
on
X""
1
x
{d}.
In
addition,
it is
clear that
FX«
\
Fx»-
l
x{d}
is
nonvoid. This completes
the
proof.
D
Now
we are
ready
to
prove
the key
lemma.
Lemma
7.9.
7x
n
is
generatedby
the
union
ofTX«
and the set
of
all
functions
F : X
n
->• X"
having
the
form
F(x\,...,
x
n
) =
(/(*i,
• • •,
x
n
),
x
2
,
x^,...,
*„),
/ : X" ->• X,
where
X\,
. .. ,
X
n
€ X.
Proof.
We can
take
out of
consideration
the
trivial
case
|X| = 1.
Thus
we
assume
|X| > 1.
For
every pair
i e
{1,...,
n}, / : X
n
-+ X,
define
the
function
F/,/
: X" ->• X"
with

7.2. Network
Completeness
for
Digraphs Having
All
Loop
Edges
207
F
it
f(xi,
...,*„)
=
(xi,...,
xt-i, f(xi,...,
x
n
),
x
i+
i,
...,*„)
(x\,
...,x
n
eX).
Thus,
by
letting
/' =
Ui
j o /, we
have
F/ / =
t/,
;
o F,
/>
o
C7,
;
.
So for
every pair
i e
{1,...,
n},
/ : X* -» X,
F,,/
e
{r
x
«U{F
: X» -> X" |
F(JCI,
...',
JC
B
)
=
(/(^i,...,
*,,),
*
2
, *
3
, • • •,
*»),
/
:X"-^X,*i,...,jc
B
€X}).
Let us
identify
X
with
a
nontrivial
finite
cyclic group with
a
generating element
g
e X.
Thus
we
also
have that
for any
whenever
otherwise,
where
x =
(x
1
,...,
x
n
) e X
n
. On the
other hand,
by
Lemma 7.3, there
exists
an
arrange-
ment
a\,...,
a
m
of X"
such that
for
every
where
But
then
p\,...,
p
m
-\
is a set of
transpositions such that
{p\,...,
p
m
-\} generates
all
permutations over
X
n
. At the
same time,
t\,...,
t
m
-\
is a set of
elementary collapsings
over
X
n
.
Thus
by the
well-known fact that
for
every
j =
1,...,
m
—
1,
(p\,..., p
m
-\,
t
}
;,}
generates
all
transformations over
X
n
, the
proof
is
complete.
7.2
Network
Completeness
for
Digraphs Having
All
Loop
Edges
We
start with
the
following.
Lemma 7.10.
Let D= (V, E) be a
strongly
connected
digraph
containing
all
loop
edges.
Using
the
notation
of
Lemma
7.1,
let
F
itj
: X
n
-> X
n
denote
any
of
F$, F$, F$, or
Utj,
where
i, j e V.
Then
Thus
F-- and F
t
j (i, j e V) are
composites
of
Junctions
in FX«
that
are
compatible with
the
graph.

208
Chapter
7.
Finite State-Homogeneous
and
Asynchronous
Automata Networks
Proof.
For
Fi(4)
}
this
is
clear.
We first
establish that
if
there
is a
directed walk
on
digraph
D
from
i to j,
then Fi,j
is a
composite
of
functions
compatible with
the
graph, where
€
e {1, 2, 3}.
Since
by
Lemma
7.1
£/,-,_,•
is a
composite
of
such,
the
result will then follow.
We
shall proceed
by
induction
on the
length
L
(the number
of
edges counting repetitions)
of
the
walk.
For L = 0, we
have
i = j and by
definition
FJJ
is
compatible with
D.
Also
when
i = j or L = 1,
clearly
F
f
j is
compatible with
X>.
Now
suppose that
i j, L > 1,
and
that
we
have
a
walk length
L + 1
from
vertex
i to
vertex
j.
Denote
the
penultimate
vertex
on the
walk
by v. If v = j,
then
Fij =
F
itV
,
or, ifv = i, F
{
j —
F
v
j.
In
either case,
we
have
a
shorter walk connecting
the
vertices
so
Fij
;
has the
required property. Otherwise
i, j, and v are
pairwise distinct,
so by the
previous lemma F,ij
is the
composite
of F's
whose
subscripts
are
among
(i, v), (v, j), j and i, and
which have
the
required property
by
induction hypothesis.
Recall that
(where
the
case
i = j is
allowed
hi the
above definition).
We
have
the
following direct
consequence
of the
above lemma.
Proposition
7.11. Consider
the
subsemigroup {Tx"}
of 7x
n
generated
by the
elements
of
TX»-
For any
strongly
connected
graph
on n
vertices containing
all
loop
edges,
this
subsemigroup
is
also generated
by a
subset
of Y
x
«
consisting
of
some
maps
compatible
with
the
graph.
Let
A =
(Z
n
,
X, 8), B =
(Z
m
,
Y,
<$')
be
networks (having
the
same basic
set Z). We
say
that
B
simulates
A by
projection
if
there exists
an H c
{!,...
,m}
such that every
8
X
: Z" ->
Z
n
(x
€ X) is an
//-projection
of a
mapping
S'
p
: Z
m
-> Z
m
(p e
Y
+
).
If
there
exists
a
X>-network
B
which simulates
a
given network
A by
projection, then
it is
said that
A can be
simulated
on V by
projection.
A
digraph
D is
called n-complete with
respect
to
simulation
by
projection
if
every network
of
size
n can be
simulated
on D by
projection.
The
following statement
is
obvious.
Proposition
7.12. Given
a
positive
integer
n > 1, a
digraph
is
n-complete with
respect
to
simulation
by
projection
if
and
only
if
it has a
strongly
connected
subdigraph
having this
property.
Consider
a
digraph
V = (V, E) and a
D-network
A =
(Z
n
,
X, 8). If (i, i) £ V for
some
i e V,
then
we
obviously have that
the ith
component
of 5
does
not
depend
on its
i
th-state variable.
In
this case
the
I'th component-automaton
of the
network must
be a
reset
automaton
without
identity.
(B = (B, X&, SB) is
called reset automaton without identity
if
for
every input letter
x e X,
{&&(b,
x) \ b e B} is a
singleton.)
On the
basis
of
this
fact,
it is
clear that
an
important special case
of the finite
automata networks
is
when
the
communication link
has all
loop edges.
In
this case
all
components
of the
network
may
depend
on
their
own
states, too.
We
shall
use the
characterization
as
follows.

7.2. Network Completeness
for
Digraphs
Having
All
Loop Edges
209
Theorem 7.13.
Given
a
positive
integer
n > , a
digraph
of
order
n
having
all
loop
edges
is
n-complete
with
respect
to
simulation
by
projection
if
and
only
if
it is
strongly
connected
and
centralized.
Proof.
Sufficiency
of the
condition follows directly
from
Proposition 7.11
and
Lemma 7.9,
since
the
members
of r
x
« are
composites
of
compatible maps
and
centralization (without
loss
of
generality
at
vertex
1)
implies that
all of 7x» is
generated
by
maps compatible
with
the
digraph.
For
necessity, obviously
T>
must clearly
be
strongly connected.
Let
q —
\Z\,
and
identify
the
elements
of Z in a fixed but
arbitrary
way
with
the
elements
{0,1,...,
q — 1} of the
modulo
q
residue
ring of
integers. Suppose
F e
7z», such that
the
image
of F
excludes exactly
one
element
of Z":
|Im
F\ = q
n
- 1,
where
Im
F
=
(F(z)
| z =
(zi,...,
z
n
)
e
Z
n
}.
Clearly,
if F is a
written
as a
composite
of
functions
on Z
n
,
then
at
least
one of
them also
has q" — I
elements
in its
image. Thus
it is
enough
to
show that such
a
function
cannot
be
a
transition
function
of a
network which
is not
centralized.
For
such
a
function
F —
(/!,...,/«)
there exist unique
a =
(a
1
,...,
«„) and
b =
(bi,...,b
n
)
such that
F
-1
(d)
= 0 and
\F
-1
(b)\
= 2.
Since
we
identify
Z
with
the
elements
of the ring of
integers modulo
q, one has the sum
(*).
Notice that
for a
bijective
F'
=
(//,..., /„')
one has
X^ez™
//(z)
=
Ec,
6
z4
n-1
~
lc
«'
hence,
it
follows, since
F is
"almost"
bijective,
Since
a ^ b,
this
sum is
nonzero
for at
least
one
component
i.
Now
suppose that
the
network
is not
centralized.
Then
for
each
i, the
component
function
/} of F
depends
on
only
j
variables with
j < n. (Of
course,
the
exact value
of
j
may
depend
on i.)
Suppose, without
loss
of
generality, these variables
are zi,
•..,
Zj. It
follows
that
the
cardinality
of
f
{
~
1
(f
{
(z\,...,
Zj•,
0,...,
0)) is a
multiple
of
q
n-j
. Thus,
for
all
components
i.
This contradicts
(*) and a ^ b, so no
such
F may be a
transition
function
of the
network.
2
Chapter
7.
Finite State-Homogeneous
and
Asynchronous
Automata Networks
Using
the
above theorem
and the
preliminary results above,
we
recover
the
following
characterization.
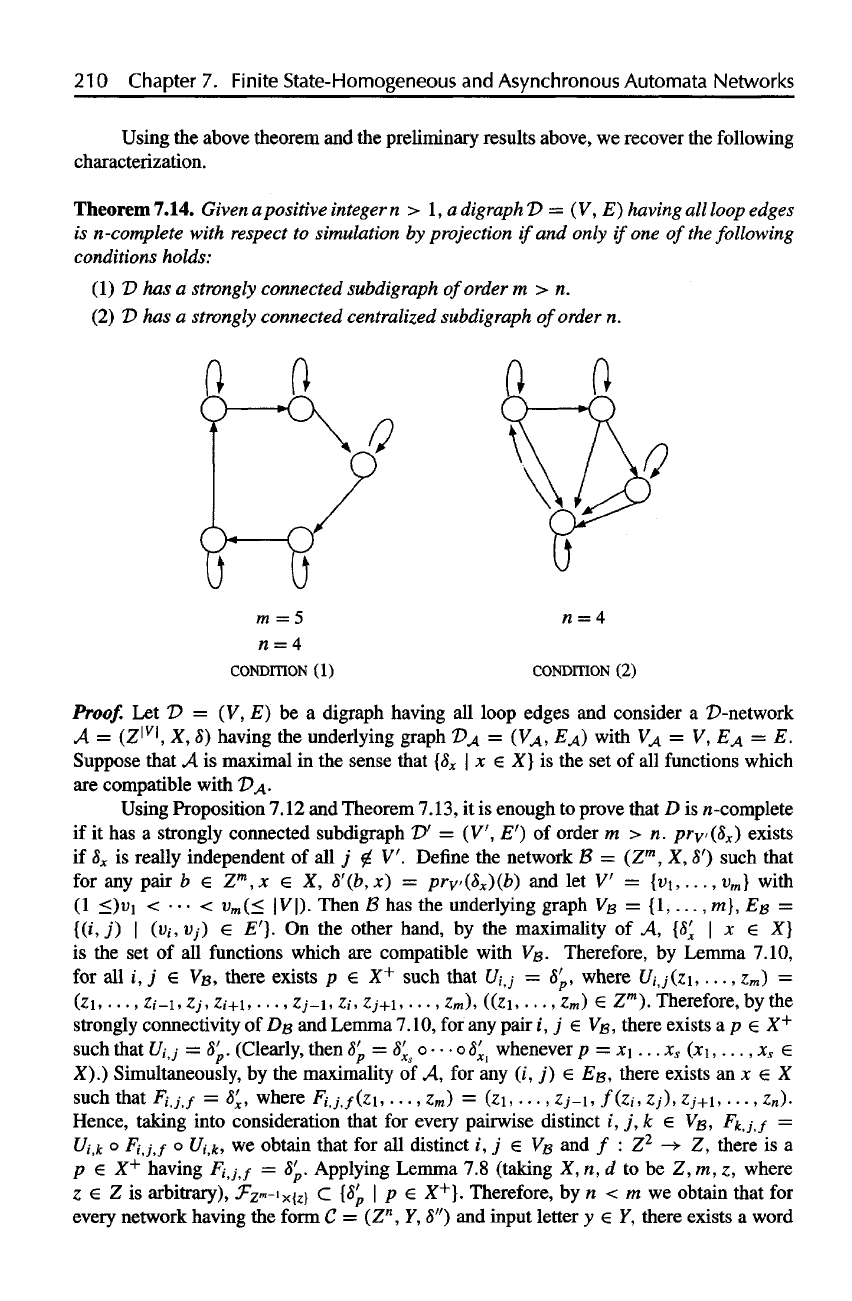
Theorem
7.14. Given
a
positive
integer
n > 1, a
digraph!)
= (V, E)
having
all
loop
edges
is
n-complete with
respect
to
simulation
by
projection
if
and
only
if
one of the
following
conditions
holds:
(1)
P has a
strongly
connected
subdigraph
of
order
m > n.
(2) D has a
strongly
connected centralized
subdigraph
of
order
n.
Proof.
Let £> = (V, E) be a
digraph having
all
loop
edges
and
consider
a
D-network
A =
(Z
|V|
,
X, 5)
having
the
underlying graph
D
A
=
(V
A
,
E
A
)
with
V
A
=
V,E
A
= E.
Suppose that
A is
maximal
in the
sense that
{8
X
\ x e X} is the set of all
functions which
are
compatible with
D
A
.
Using
Proposition
7.12
and
Theorem 7.13,
it is
enough
to
prove that
D is
n-complete
if
it has a
strongly connected subdigraph
D'
= (V, E') of
order
m > n.
pr
V
'(8
x
)
exists
if
S
x
is
really independent
of all ; & V.
Define
the
network
B =
(Z
m
,
X, 8')
such that
for
any
pair
b €
Z
m
,x
e X,
8'(b,x)
=
pr
V
'(8
x
)(b)
and let V =
{vi,...,v
m
}
with
(1
<)t>i
< • • • <
v
m
(<
|
V|). Then
B has the
underlying graph
VB =
{!,...,
m}, EB =
{(i,
j) I
(vi,Vj)
e
E'}.
On the
other hand,
by the
maximality
of A,
[8'
x
\ x e X}
is the set of all
functions which
are
compatible with
VB-
Therefore,
by
Lemma
7.10,
for
all i, j € VB,
there
exists
p e X
+
such that
U{j =
8'
p
, where
Uij(zi,...,
z
m
) =
(zi,...,
zt-i,
Zj,
Zi+\,...,
Zj-i,
Zi,
Zj+i,...,
z
m
),
((zi,...,
z
m
) €
Z
m
). Therefore,
by the
strongly
connectivity
of DB and
Lemma 7.10,
for any
pair
i,j e VB,
there exists
a p e X
+
such that
Ufj
=
8'
p
. (Clearly, then
8'
p
=
8'
Xs
o • • • o
8'
Xi
whenever
p = x\
...x
s
(x\,
...,x
s
€
X).) Simultaneously,
by the
maximality
of A, for any (i, j) e E&,
there exists
an x e X
such
that
F
iijt
f
=
S'
x
, where
F
ijtf
(zi,...,
z
m
) =
(zi,...,
Zj-i,
f(z
f
,
Zj),
z
j+
i,...,
z
n
).
Hence, taking into consideration that
for
every pairwise distinct
i, j, k e VB,
Fkj,/
=
Ut,k
o
Fij
t
f
o UM, we
obtain that
for all
distinct
i, j e VB and / : Z
2
-> Z,
there
is a
p
e X
+
having
Fjj
t
f
=
8'
p
. Applying Lemma
7.8
(taking
X, n, d to be Z, m, z,
where
Z
e Z is
arbitrary),
Fz
m
-
l
x{z}
C
{8'
p
\ p e
X
+
}.
Therefore,
by n < m we
obtain that
for
every network having
the
form
C =
(Z
n
,
Y, 8") and
input letter
y E Y,
there exists
a
word
