Дипломная работа - Асимптотические методы исследования нестационарных режимов в сетях случайного
Подождите немного. Документ загружается.


Просуммируем левые и правые части уравнений системы (2.7) и
получим равенство
0
,
2
,
2110
x
x
RRRR
x
. (2.8)
С учетом того, что
1210102
102110
2
RRRRRRGR
RGRGRRRR
равенство (2.8) принимает вид
0
,,
1
x
x
R
x
. (2.9)
Уравнение (2.9) является однородным линейным уравнением с
частными производными первого порядка. Для того чтобы его решить
составим уравнение
1
1 R
dxd
,
его решение
dssRsCx
0
1
, тогда
.
0
1
dssRsxC
Общее решение уравнения (2.9) имеет вид
dssRsxx
0
1
,
, (2.10)
где
- произвольная дифференцируемая функция, аналитическое
выражение которой найдем из начальных условий.
Пусть распределение в начальный момент времени
,xq 0,x
где
xq
некоторая плотность распределения. Тогда
,0, xxx q
следовательно
dssRsxx
0
1
, q
. Возьмем в качестве начальной
плотности распределения
0
x-xxq
, где
- дельта-функция Дирака, а
00
ix
,
0
i
- число заявок в источнике повторных вызовов в начальный
момент времени.
21
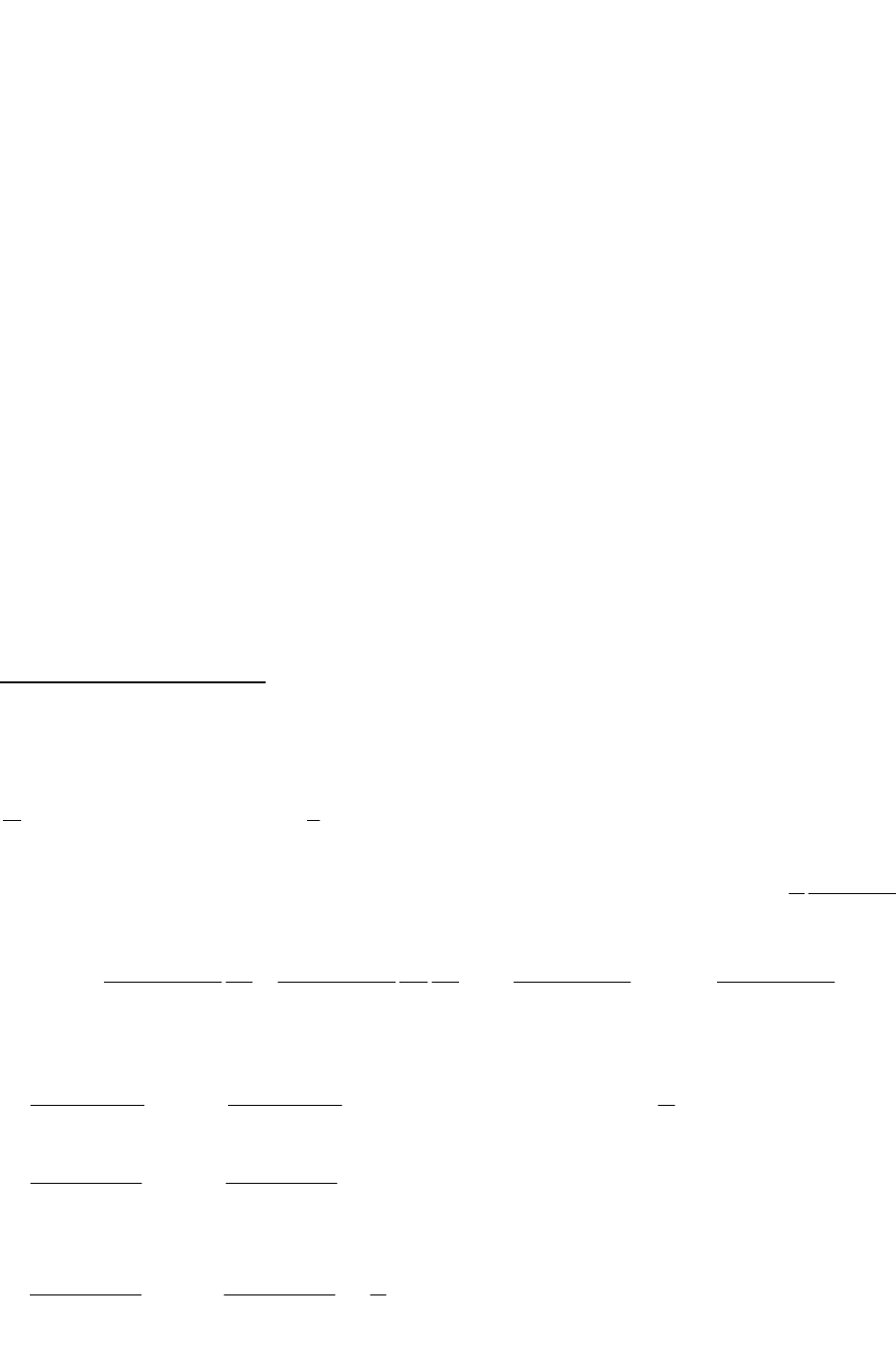
Таким образом
dssRsxxx
0
10
,
, из свойств функции
Дирака следует, что
dssRsxx
0
10
.
То есть мы получили, что
xx
,
x
имеет смысл асимптотического
среднего.
Из приведенных рассуждений вытекает еще одно важное следствие, а
именно
10:
имеет место
1
R
, тогда
0x
(отрицательная функция
x
противоречит смыслу задачи). В нашем случае
1
R
совпадает с
пропускной способностью системы.
Перейдем ко второму приближению, в котором будем искать
распределение отклонения от асимптотического среднего.
Второе приближение
В исходной системе уравнений (2.1) сделаем замену переменных
,,,
1
,,,
1
222
ytiPyxit
T
kk
.
Заметим, что в новых обозначениях производная по времени
t
tiP
k
,1
равна
y
y
x
y
t
y
y
y
t
y
kkkk
,,,,,,,,
2
. С
учетом этого система (2.1) примет вид
,,,
1
,,,,
,,,,
210
00
2
y
a
yyG
y
y
x
y
,,,
,,,,1
,,,,
0
01
11
2
y
yyG
y
y
x
y
(2.11)
.,,,,
,,2,,
1,,,,
21
12
22
2
yy
yy
ay
y
x
y
22

Решение системы уравнений (2.11) аналогично решению системы (2.2),
но проводится в три этапа.
1 этап . В системе дифференциальных уравнений (2.13) сделаем предельный
переход при
0
и предположим, что
,,,lim
0
yy
kk
, получим
,,
1
,,
210
y
a
yyG
,,,1
01
yGyG
(2.12)
,,
1
12
yGy
a
.
Решим эту систему аналогично тому, как решили систему уравнений
(2.3). Введем функцию
2
0
,,
k
k
yy
и выразим через нее
,y
k
,
получим
,,
12
1
,
2
0
y
GaG
G
y
,,
12
,
2
1
y
GaG
G
y
(2.13)
,,
12
,
2
2
2
y
GaG
aG
y
где
,y
асимптотическая плотность распределения отклонения числа
заявок в источнике повторных вызовов от асимптотического среднего.
2 этап . Функции
,,y
k
будем искать с точностью до
в форме
.,,,, oyhyRy
kkk
(2.14)
Найдем вид функций
,
0
yh
,
,
1
yh
и
,
2
yh
. Для этого в системе
дифференциальных уравнений (2.11) все функции с аргументом
2, yy
разложим в ряд по приращению аргумента
y
, ограничимся слагаемыми
порядка
. Получим
,,,
1
,,,,
,,
210
0
y
a
yyG
y
y
x
y
y
yGyG
y
y
x
,,
,,),,(1
,,
0
01
1
(2.15)
23
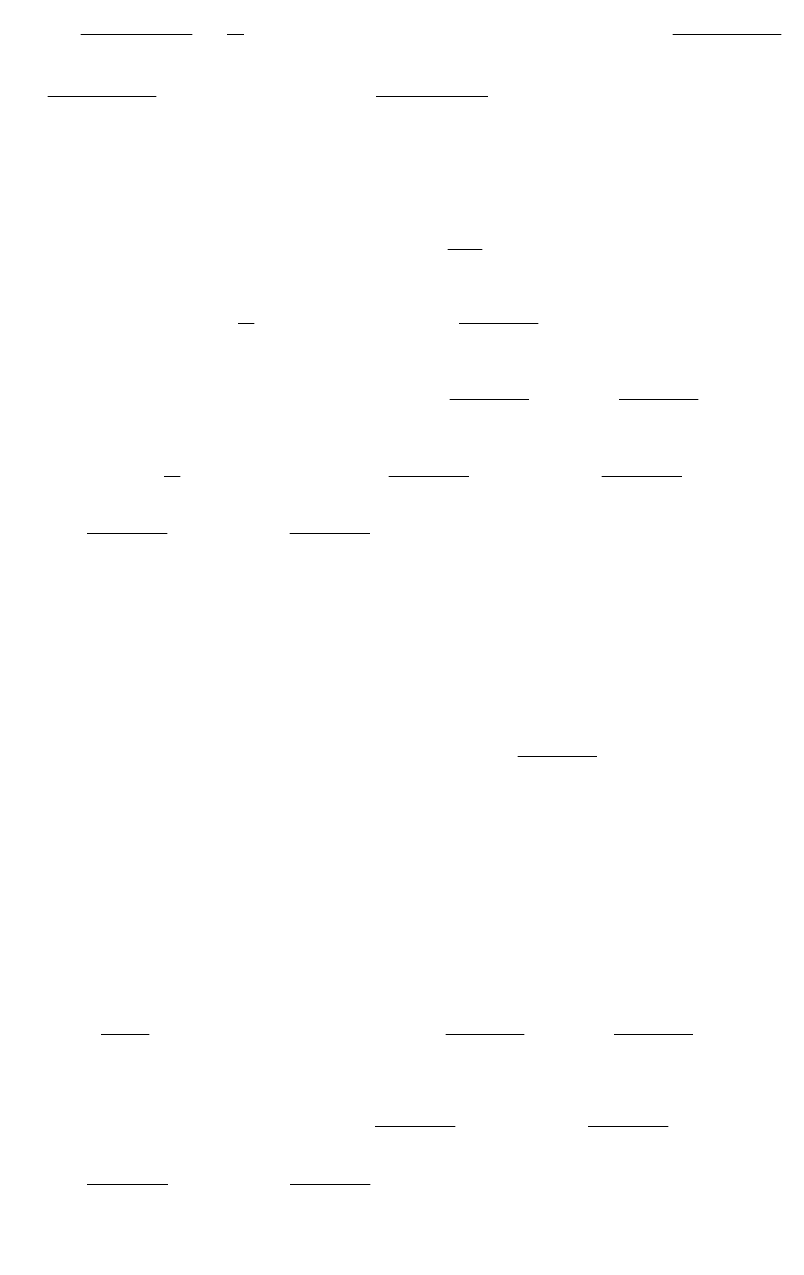
.
,,
,
,,
,,
2,,,,
1,,
2
2
1
1
12
2
y
y
y
y
y
y
y
yGy
ay
y
x
В уравнения (2.15) подставим
,,y
k
в форме (2.14), приведем
подобные и получим систему неоднородных линейных алгебраических
уравнений относительно
2,0,, kyh
k
вида
y
y
Rxyh
a
yhyhG
,
,
1
,,
0210
,
y
y
R
y
y
RxyhGyhG
,,
,1,
0110
, (2.16)
.
,,
,
2
,
,
1
,
21
1221
y
y
R
y
y
R
y
y
R
y
y
Rxyh
a
yhG
Нетрудно увидеть, что между уравнениями этой системы есть
зависимость и ранг матрицы системы равен, следовательно, чтобы решение
уравнений (2.16)существовало, необходимо выполнение равенства
.0
,
1
y
y
Rx
(2.17)
Из однородного линейного уравнения с частными производными
первого порядка (2.9) мы знаем, что
1
Rx
. Таким образом, можно
сделать вывод, что система (2.16) разрешима. При условии, что функция
,
1
yh
известна, решение можно записать в виде
y
y
R
y
y
RxyhG
G
yh
,,
,1
1
,
0110
,
.
,,
,
2
,
,,
21
1212
y
y
R
y
y
R
y
y
R
y
y
RxyhGayh
(2.18)
Теперь все готово, для того, чтобы найти функцию
,y
. Перейдем к
третьему этапу.
24
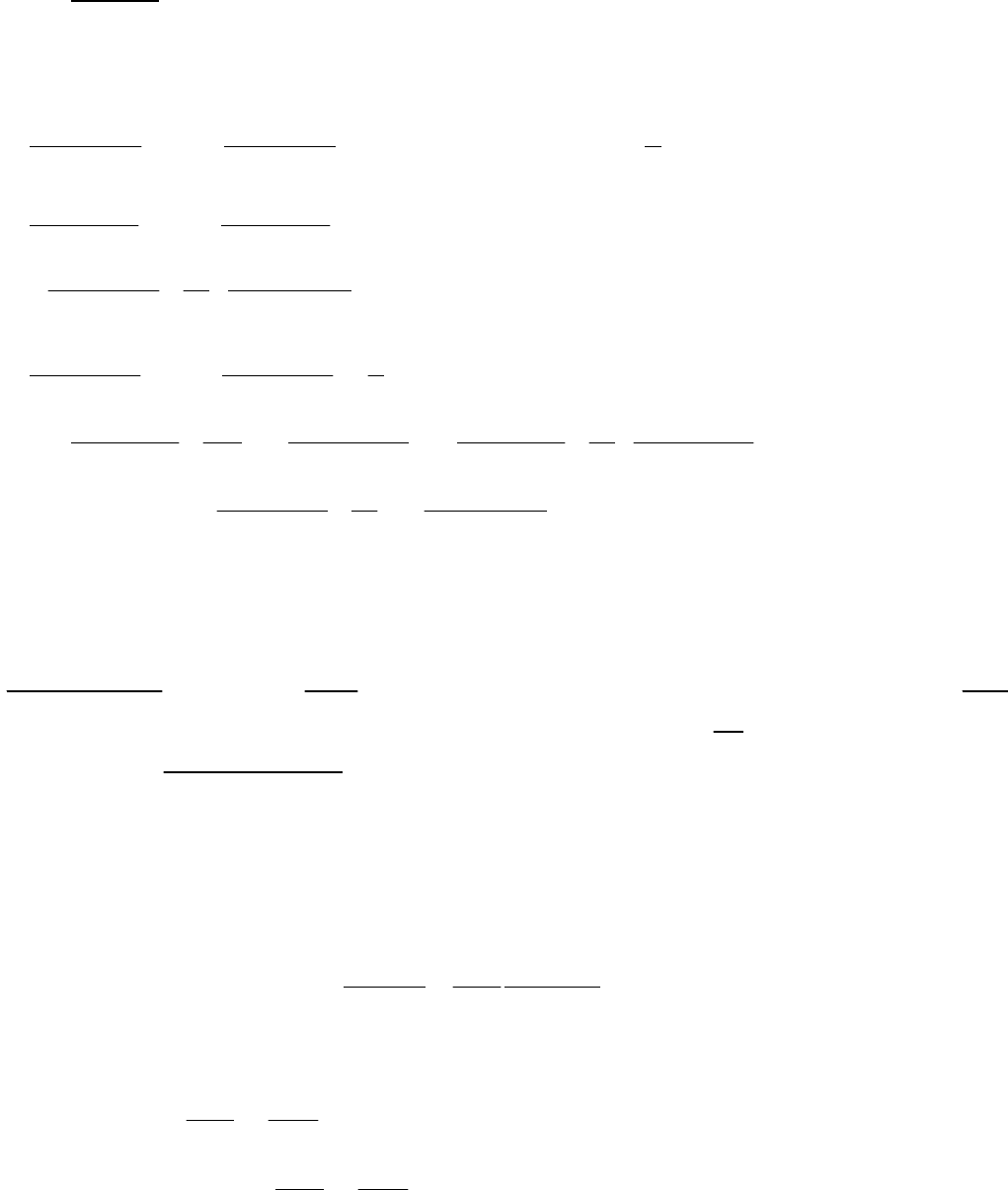
3 этап . В системе дифференциальных уравнений (2.11) все функции с
аргументом
2, yy
разложим в ряд по приращению аргумента
y
,
ограничиваясь слагаемыми порядка
2
, получим
,,,
1
,,,,
,,,,
210
00
2
y
a
yyG
y
y
x
y
,
,,
2
,,
,,,,1
,,,,
2
0
22
0
01
11
2
y
y
y
y
yGyG
y
y
x
y
(2.19)
.
,,
2
,,
,
,,
2
,,,,
2
4,,
2
,,,,
1,,,,
2
2
22
2
2
2
1
22
1
2
1
22
1
12
22
2
y
y
y
y
y
y
y
y
y
y
y
y
y
yGy
ay
y
x
y
Теперь подставим в уравнения (2.19)
,,y
k
в форме (2.14) и
просуммируем левые и правые части уравнений, будем иметь
.
,
4
2
1
,,,
2,,,,
,
2
2
2
10211
0210
y
y
R
RRyhyhyh
yh
y
yhyhyh
y
x
y
(2.20)
Подставляя вместо
,
0
yh
и
,
2
yh
их выражения, полученные на
втором этапе получим для
,y
уравнение Фоккера-Планка
2
2
,
2
,
y
yAу
, (2.21)
где
.42
22
22
2
1
0211
2
01
2
112
01
RRRRaRaRa
Rxa
G
R
G
R
xRa
RaRaRxa
G
R
G
R
xxA
Нормированным решением полученного одномерного уравнения
диффузии [8] является плотность нормального распределения вероятностей с
нулевым средним и дисперсией
25

0
2
dssA
. (2.22)
26
3. Исследование нестационарной сети случайного доступа со
статическим протоколом в условиях большой задержки
Исследуем сеть связи, функционирование которой изложено в разделе
1, в условиях большой задержки. В этом случае удобнее рассматривать
случай, когда интенсивность каждой заявки в ИПВ равна
. Структура такой
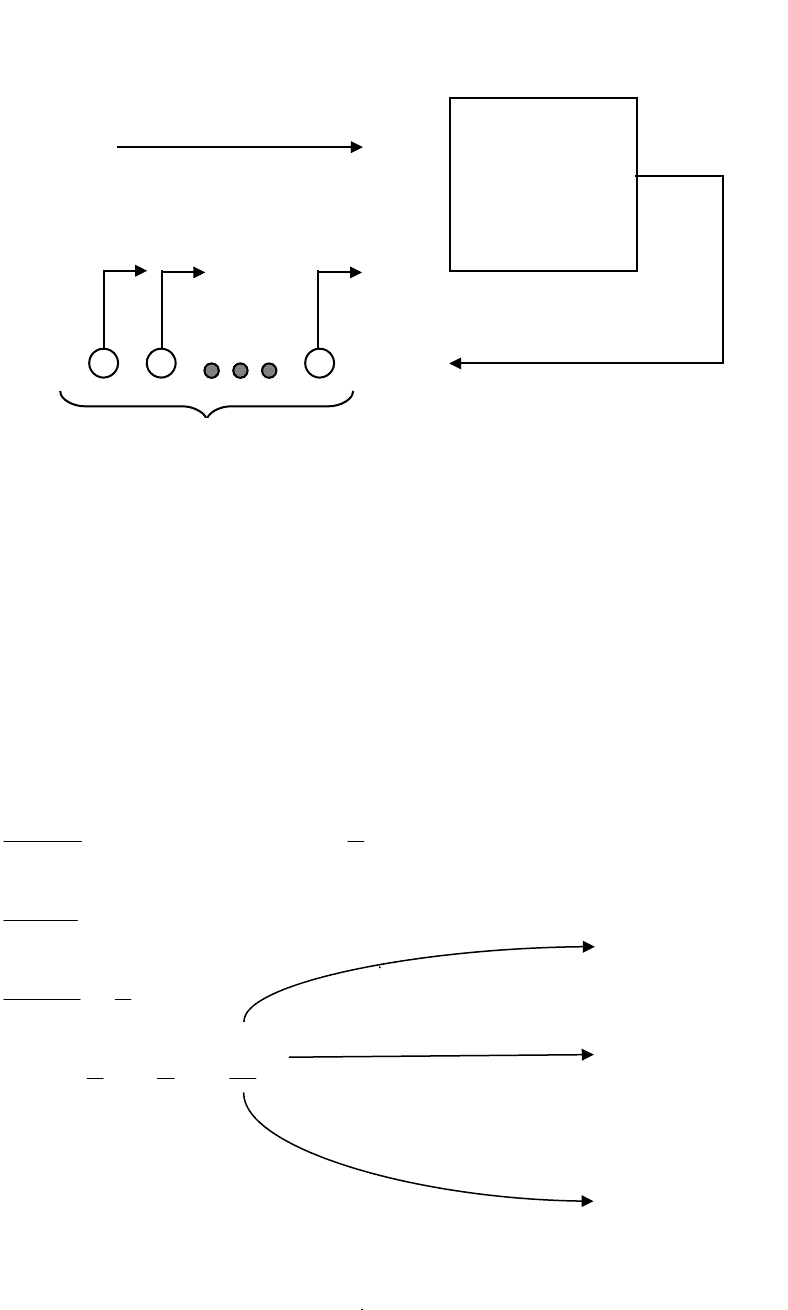
СМО имеет вид рис. 3.1.
Рис. 3.1 – Модель системы массового обслуживания
Вероятности переходов из состояния системы
11
,ki
в произвольный
момент времени t в состояние
22
,ki
за бесконечно малый интервал времени
t
показаны на рис. 3.2, рис. 3.3, рис. 3.4.
Выпишем уравнения статистического равновесия для нестационарного
распределения процесса
tkti ,
, описывающего функционирование сети
,,
1
,,
,
210
0
tiP
a
tiPtiPi
t
tiP
,,11,,1
,
001
1
tiPitiPtiPi
t
tiP
(3.1)
,,1,11,2,
1,
2112
2
tiPtiPitiPtiP
at
tiP
где
.1,,,
1
a
27
tot
0,i
1,i
toti
toti 1
0,i
1,1i
λ
1
i
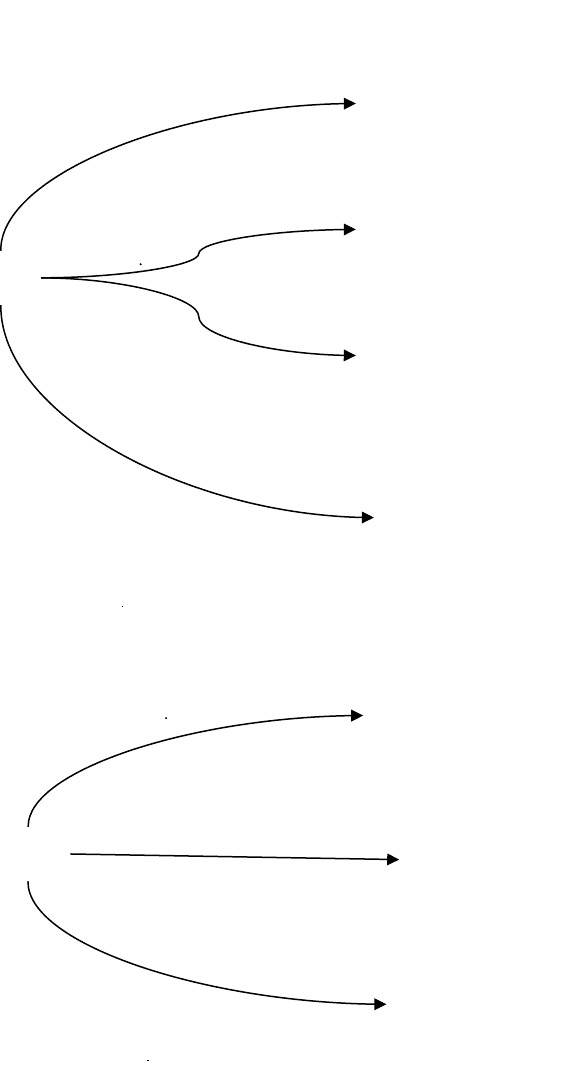
Рис. 3.2 – Возможные переходы из состояния
0,i
Рис. 3.3 – Возможные переходы из состояния
1,i
Рис. 3.4 – Возможные переходы из состояния
2,i
28
tot
1,i
2,2i
toti
toti 1
1,i
2,1i
0,i
tot
2,i
2,1i
tot
tot
1
tot
1
1
2,i
0,i

Найти точное аналитическое решение системы (3.1) практически
невозможно, но можно решить асимптотически в условиях большой
задержки, то есть при
0
.
Первое приближение
Для асимптотического решения системы (3.1) сделаем замену
переменных
,,,
1
,,, xtiPxit
kk
. В результате замены
производится переход от дискретной переменной
...,2,1,0i
к
непрерывной переменной
0xx
.
В новых обозначениях
,,,,,1 x
t
x
t
tiP
kkk
. Тогда
система (3.1) примет вид
,,,
1
,,,,
,,
210
0
x
a
xxx
x
,,,,,,,1
,,
001
1
xxxxx
x
(3.2)
.,,
,,,,2,,
1,,
2
112
2
x
xxxx
a
x
Получим вид решения системы (3.2), которую будем решать в два
этапа.
1 этап. Считая
0
и предполагая, что
,,,lim
0
xx
kk
, будем иметь
,,
1
,,
210
x
a
xxx
,,,1
01
xxxx
(3.3)
,,
1
12
xxx
a
.
Выразим
,x
k
через функцию
2
0
,,
k
k
xx
и получим
,,
12
1
,
2
0
x
xGxaG
xG
x
29

,,
12
,
2
1
x
xGxaG
xG
x
(3.4)
,,
12
,
2
2
2
x
xGxaG
xaG
x
где
,xxG
,x
- асимптотическая плотность нормированного числа
заявок в источнике повторных вызовов.
Обозначим
.
12
,
12
,
12
1
2
2
2
2
1
2
0
xGxaG
xaG
xR
xGxaG
xG
xR
xGxaG
xG
xR
(3.5)
Заметим, что из системы (3.3) следуют равенства
,
2
10
a
xR
xRxRxG
,1
01
xRxGxRxG
(3.6)
xRxG
a
xR
1
2
.
Осталось найти вид функции
,x
. Для этого перейдем ко второму
этапу.
2 этап . В системе (3.2) разложим функции по приращению аргумента
x
,
ограничиваясь слагаемыми порядка
, получим систему
,,,
1
,,,,
,,
210
0
x
a
xxxG
x
,,,,,,,1
,,
001
1
xx
x
xxGxxG
x
(3.7)
.
,,
,,,,
,,
2,,,,
1,,
2
21
1
12
2
x
x
xxx
x
x
x
xxGx
a
x
Просуммируем полученные уравнения, поделим на
и перейдем
0
lim
. Тогда будем иметь
,2
,
2110
xxRxxRxRxxR
x
x
. (3.8)
С учетом того, что
30
