Дипломная работа - Асимптотические методы исследования нестационарных режимов в сетях случайного
Подождите немного. Документ загружается.

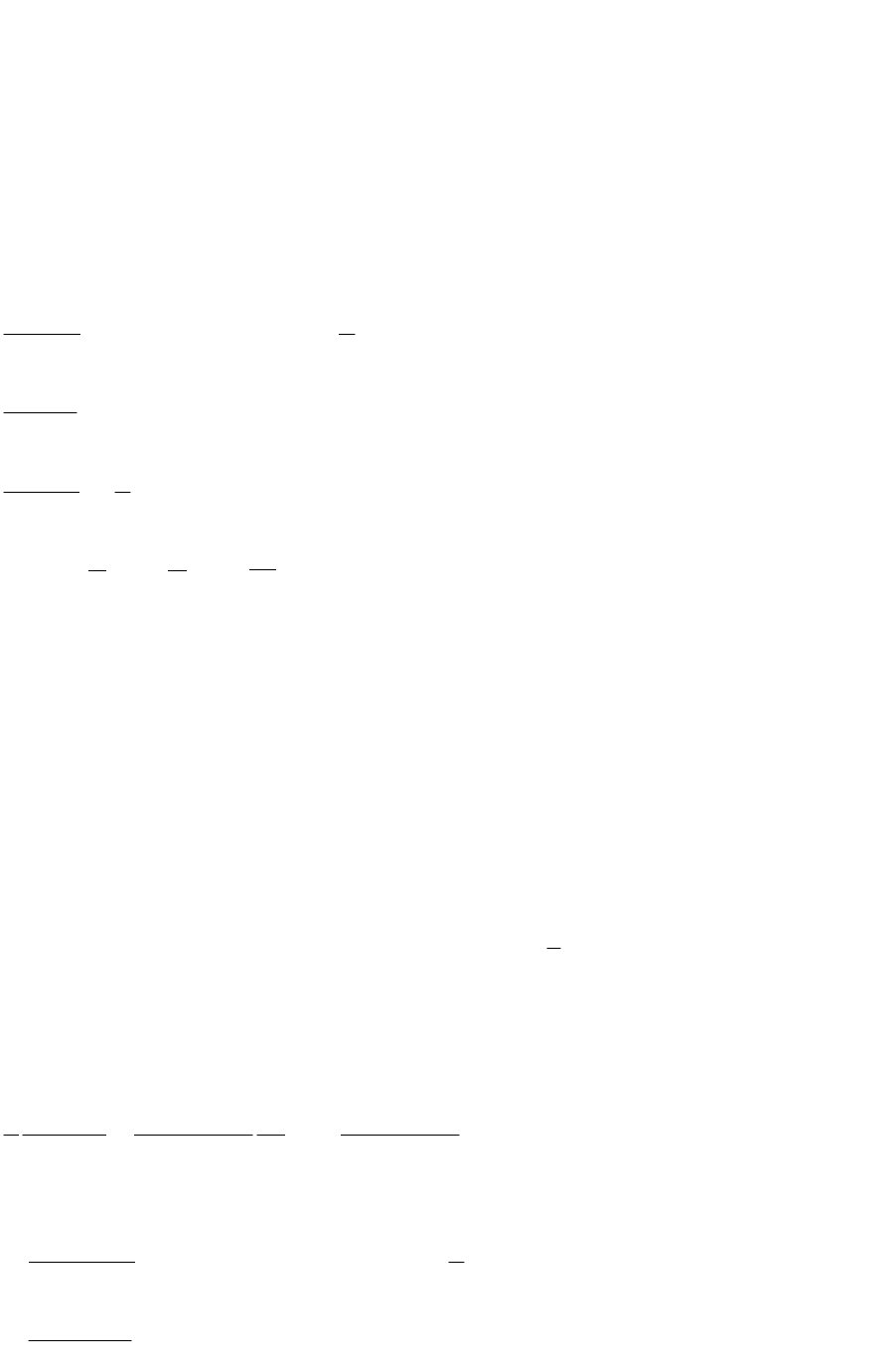
Таким образом, можно записать систему конечно-разностных
уравнений для вероятностей
tiP
k
,
состояний системы:
1,,1,,,
02110
itotiPttitPtitPttiP
0,,1,,,
1001
itotiPttitPtitPttiP
2,,1,1,2,
21112
itotiPttitPtitPttiP
следовательно, в нестационарном режиме, эти вероятности удовлетворяют
системе дифференциально-разностных уравнений
tiP
a
tiPtiP
t
tiP
,
1
,,
,
210
0
,
tiPtiPtiP
t
tiP
,1,,1
,
001
1
, (1.1)
tiPtiPtiPtiP
at
tiP
,1,1,2,
1,
2112
2
,
где
,
,
,
1
a
1
,
решить которую практически невозможно, но можно решить асимптотически
в условиях «большой загрузки», т.е. при
S
,
S
, где
S
пропускная
способность исследуемой сети связи (верхняя граница множества тех
значений загрузки
, для которых в системе существует стационарный
режим).
Рассмотрим исходную систему уравнений (1.1) и произведем в ней
замену переменных:
S
,
2
t
,
xi
,
,,,
1
xtiP
kk
. В результате
замены производится переход от дискретной переменной
...,1,0i
к
непрерывной переменной
0xx
. В новых обозначениях производная равна
,,,,,1
2
x
t
x
t
tiP
kkk
.
Тогда систему (1.1) перепишем
,,
1
,,,,
,,
210
0
2
x
a
xx
x
,
,,,,,,1
,,
001
1
2
xxx
x
, (1.2)
11

.,,
,,,,2,,
1,,
2
112
2
2
x
xxx
a
x
Получим вид решения системы (1.2), которую будем решать в три
этапа.
1 этап. В уравнениях (1.2) устремим
0
и обозначим
,,,lim
0
xx
kk
,
заметим что,
S
0
lim
. Будем иметь
,
1
,,
210
x
a
xxS
,
,,1
01
xSxS
, (1.3)
,,
1
12
xSx
a
.
Выразим
,x
k
через
2
0
,,
k
k
xx
и получим
,
12
1
,
2
0
x
GaG
G
x
,
,
12
,
2
1
x
GaG
G
x
, (1.4)
,
12
,
2
2
2
x
GaG
aG
x
.
где
,SG
,x
– асимптотическая плотность распределения
вероятностей нормированного числа заявок в ИПВ.
Введем обозначения
,
12
,
12
,
12
1
2
2
2
2
1
2
0
GaG
aG
R
GaG
G
R
GaG
G
R
(1.5)
(
k
R
- это асимптотическая вероятность того, что обслуживающий прибор
находится в состоянии k). Из системы (1.3) следуют равенства, связывающие
0
R
,
1
R
,
2
R
и выглядят так
,
2
10
a
R
RGR
,1
01
GRRG
(1.6)
12
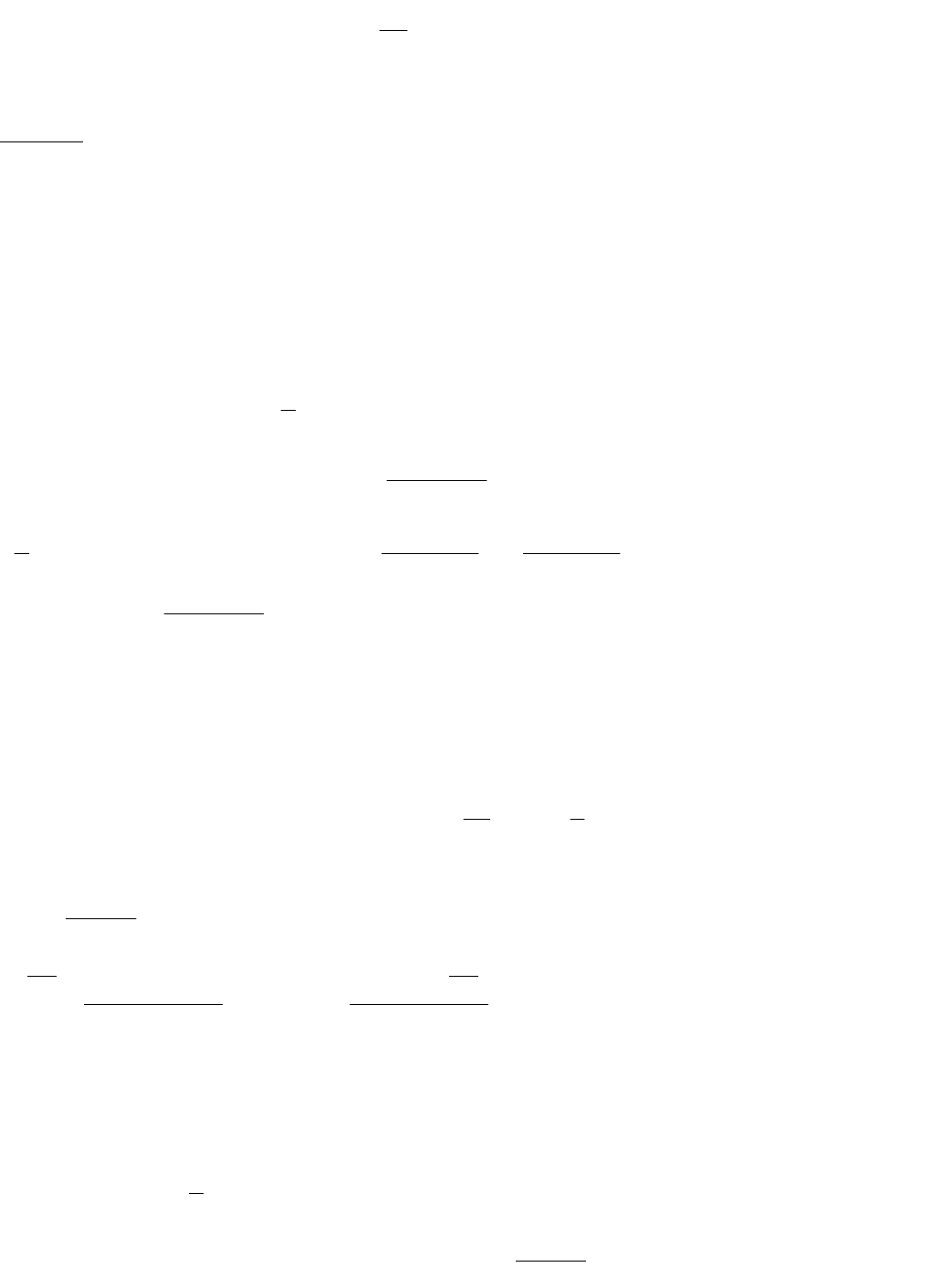
1
2
GR
a
R
.
Найдем вид функции
,x
. Для этого перейдем ко второму этапу.
2 этап . Неизвестные функции
,,x
k
будем искать с точностью до
в
следующем виде
oxhxRx
kkk
,,,,
, (1.7)
Определим вид функций
,xh
k
, для этого в системе уравнений (1.2)
разложим функции с аргументом
2, xx
в ряд по приращению
аргумента
x
(ограничиваясь двумя слагаемыми), будем иметь
,,
1
,,,,
210
x
a
xx
,
x
x
xx
,,
,,,,1
0
01
, (1.8)
.
,,
,,
,,,,
2,,,,
1
2
2
11
12
x
x
x
x
x
x
x
xx
a
В полученные уравнения подставим
,,x
k
в форме (1.7), заменим
разностью
S
, сумму
S
на G и не учтем слагаемые, имеющие
порядок
2
. Получим
,,,,,,
2
2
1100
xh
a
x
a
R
xhxRxGhxRG
,
,
,
,,,1,1
0
0011
x
x
R
xGhxRGxhGxRG
(1.9)
.
,
,,
,,
2,,,
1
,
1
22211
1122
x
x
SRxShxRS
x
x
R
x
x
R
SxGhxRGxhS
a
xRS
a
Теперь приведем подобные слагаемые, учтем равенства (1.6), и
получим неоднородную линейную систему алгебраических уравнений для
нахождения неизвестных функций
,,,,,
210
xhxhxh
такого вида
,,
1
,,
0210
xRxh
a
xhxGh
,
x
x
RxRxRxhGxGh
,
,,,1,
01010
, (1.10)
13

.
,,,
2,,
1
,
211121
x
x
SR
x
x
R
x
x
SRxRxh
a
xGh
Нетрудно заметить, что ранг матрицы однородной системы
алгебраических уравнений, соответствующей (1.10) равен двум.
Следовательно, для того, чтобы система была разрешима, необходимо, чтобы
ранг расширенной матрицы этой системы был равен двум, т.е. чтобы
выполнялось следующее равенство
0
,
2
2110
x
x
SRRSRR
. (1.11)
С учетом того, что
,
2
1
210102102110
SR
RRRSRRGSRRSGRSGSRRSRR
равенство
(1.11) принимает вид
0
,
1
x
x
SR
. (1.12)
Равенство нулю производной противоречит смыслу задачи,
следовательно
1
RS
, т. е. пропускная способность исследуемой сети связи
равна асимптотической вероятности того, что обслуживающий прибор
«обслуживает», на рис. 1.5 продемонстрирован этот результат.
14
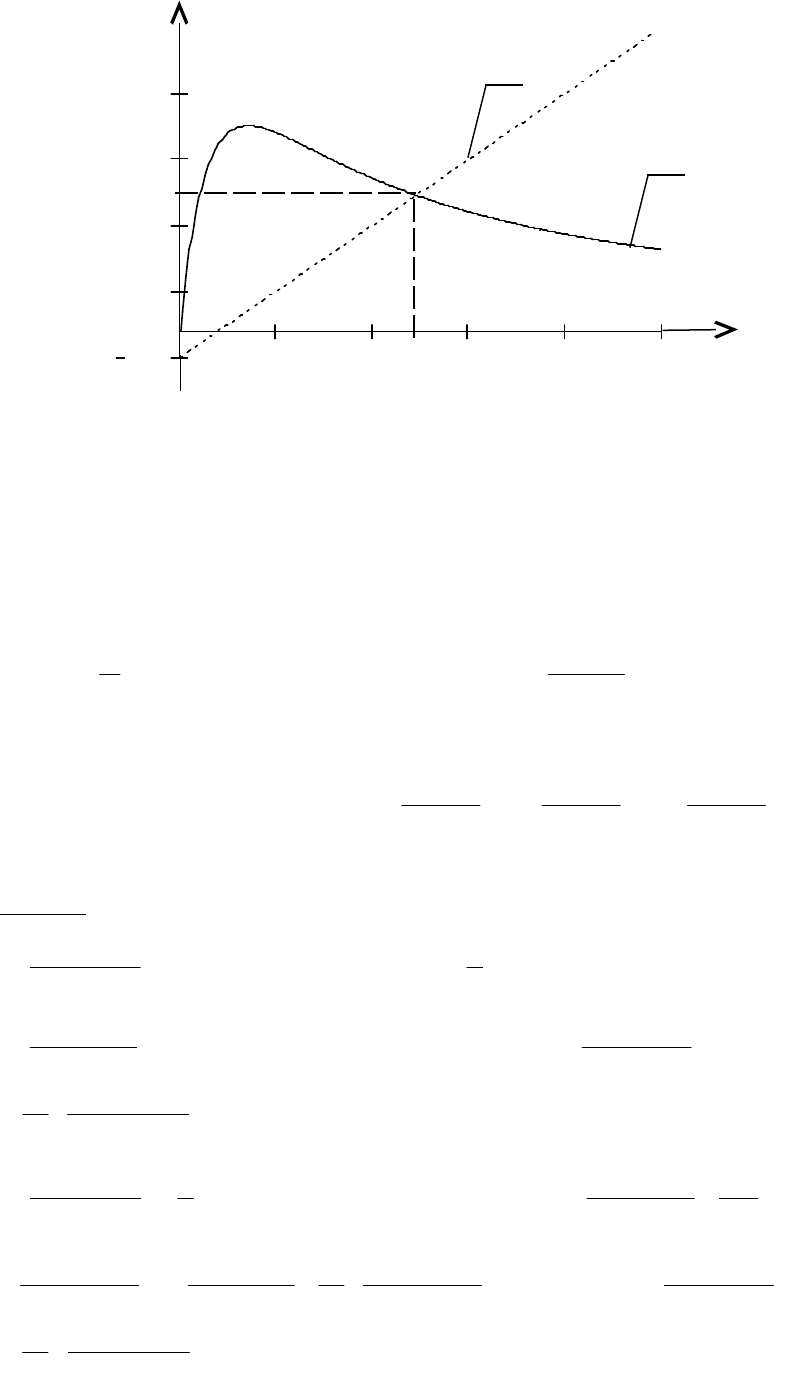
0 1 2 3 4 5
0.027
0.04
0.11
0.17
0.24
Рис. 1.5
Таким образом, мы выяснили, что система (1.10) разрешима. Ее
решение можно записать так
x
x
RxRxRxhG
G
xh
,
,,,1
1
,
01010
,
,
1
xh
- произвольная функция, (1.13)
x
x
SR
x
x
R
x
x
SRxRxGhaxh
,,,
2,,,
211112
.
Перейдем к третьему этапу.
3 этап . Запишем уравнения системы (1.2) с точностью до
2
, получим
,,
1
,,,,
,,
210
0
2
x
a
xx
x
,
,
,,
2
,,
,,,,1
,,
2
0
22
0
01
1
2
x
x
x
x
xx
x
(1.14)
2
4,,
2,,,,
1,,
2
1
12
2
2
x
x
xx
a
x
.
,,
2
,,
,,
,,
2
,,,,
2
2
22
2
2
2
1
22
1
2
1
2
x
x
x
x
x
x
x
x
x
x
x
15
S
G
*
G
1
R
G
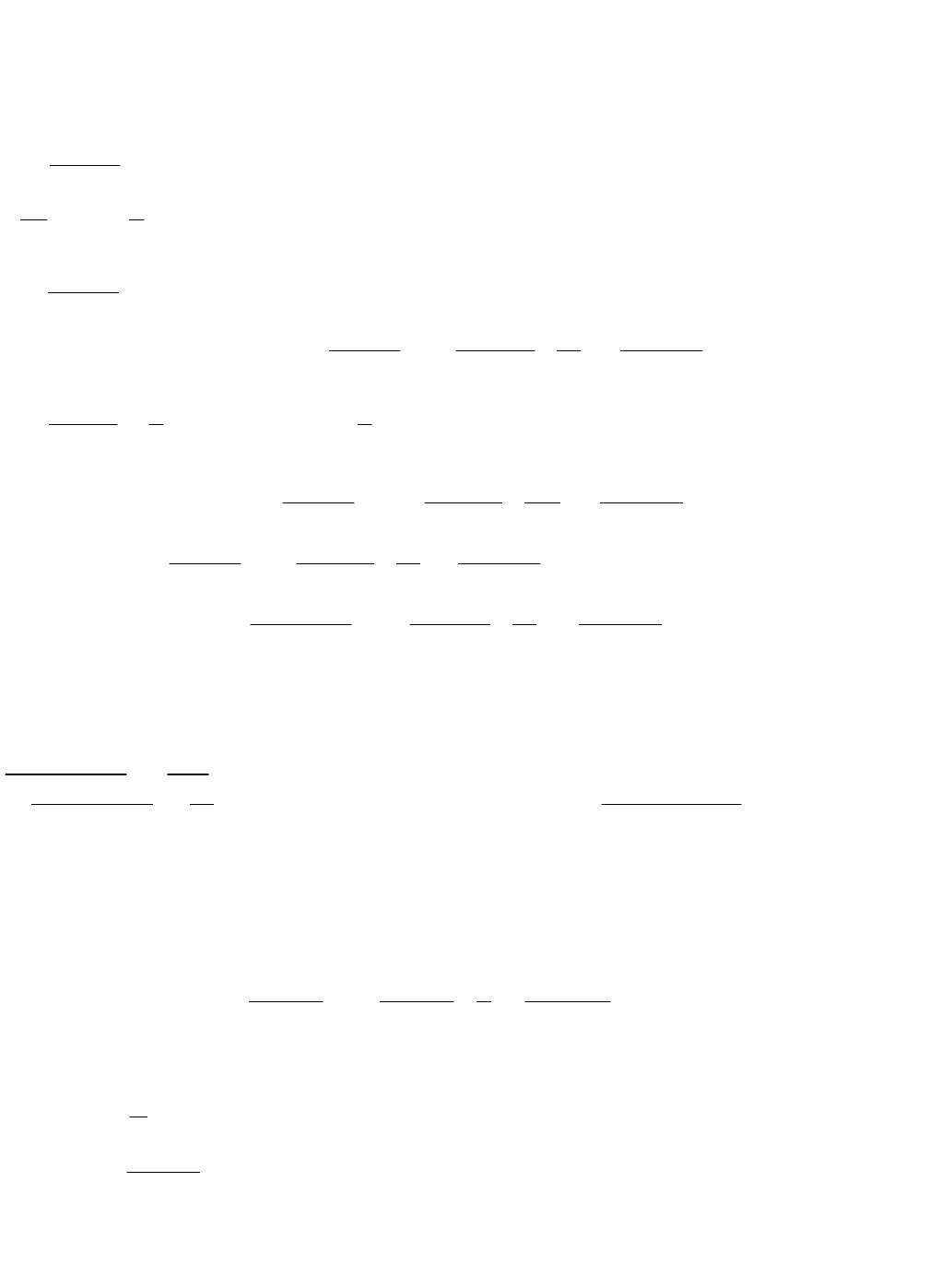
Как и на втором этапе в полученные уравнения подставим
,,x
k
в
форме (1.7), заменим
разностью
S
, сумму
S
на G и не учтем
слагаемые, имеющие порядок выше
2
, получим
,,,
,,,,
,
2
2
11000
2
xh
a
x
a
R
xhxRxhGxRG
x
R
,
,
2
,,
,,
,),(1,1
,
2
2
0
2
0
2
000
0111
2
x
x
R
x
xh
x
x
RxhxhS
xRGxhGxRG
x
R
(1.15)
,,
1
,
1,
1222
2
xRGxhS
a
xRS
a
x
R
.
,
2
,,,
,
,
,
2
,,
,
,
2
4,
2
,
2,
2
2
2
2
2
2
2
2
2
2
2
1
2
1
2
11
2
2
1
2
1
2
11
x
x
SR
x
xh
S
x
x
SxhS
xRS
x
x
R
x
xh
x
x
Rxh
x
x
SR
x
xh
S
x
x
RSxhS
Просуммировав все уравнения системы (1.15), получим равенство для
нахождения
,x
.
,
4
2
1,
2,,,2,
,
2
2
2110
212110
x
x
SRRSRR
x
x
RRxShxhxShxh
x
x
(1.16)
Подставляя выражения для
,xh
k
, найденные на втором этапе, для
,x
получим уравнение Фоккера-Планка
2
2
2
,
2
1,,
x
x
B
x
x
A
x
, (1.17)
где
.422
,211
2110210
2
2
1
SRSRRRSGSRRSGSaR
G
SG
B
R
G
S
A
Решим уравнение (1.17) с помощью преобразования Лапласа по x.
Левую и правую части уравнения умножим на
xexp
и проинтегрируем.
16
С учетом обозначения
,e,
0
dxx
x
и свойств этой функции
уравнение (1.17) приобретет вид
.
,0
2
,0
2
,
2
,
22
2
2
x
BB
A
B
A
d
d
(1.18)
Таким образом, мы перешли от уравнения Фоккера-Планка с
постоянными коэффициентами к обыкновенному дифференциальному
уравнению, решение которого с точностью до неизвестных
C
,
,0
и
,0
записывается следующим образом
.e
,0
2
,0
2
ee,
2
2
2
2
2
2
2
0
22
22
ds
s
sB
s
B
AC
s
B
A
B
A
B
A
(1.19)
Для того чтобы получить окончательное решение уравнения (1.17)
нужно провести дополнительное исследование, которое бы показало
поведение исследуемого процесса в окрестности нуля. Используя
асимптотику
S
, это не удается сделать.
Предположим, что сеть связи функционирует в стационарном режиме,
тогда (1.17) перепишется в виде
.02
22
2
dx
xd
B
A
dx
xd
(1.20)
Следовательно, в стационарном режиме асимптотическое
распределение вероятностей нормированного числа заявок в источнике
повторных вызовов подчиняется экспоненциальному закону с параметром
2
2
B
A
и
x
имеет вид
.0,2exp2
22
x
B
A
B
A
x
(1.21)
17
2. Исследование неоднородной нестационарной сети случайного
доступа с динамическим протоколом в условиях перегрузки
Рассмотрим сеть связи, описанную в разделе 1, в которой
интенсивность входящего потока зависит от времени и равна
T
t
, где Т –
некоторый интервал времени, в течение которого функционирует сеть связи.
Структура сети изображена на рис. 2.1.
Рис. 2.1 – Модель системы массового обслуживания
В нестационарном режиме распределение
...,1,0,2,0,,, ikktkitiPtiP
k
удовлетворяют системе дифференциально-разностных уравнений вида
,,
1
,,
,
210
0
tiP
a
tiPtiP
T
t
t
tiP
,,1,,1
,
001
1
tiPtiP
T
t
tiP
T
t
t
tiP
(2.1)
,,1,1,2,
1,
2112
2
tiP
T
t
tiPtiP
T
t
tiP
T
t
at
tiP
где
T
t
T
t1
,
,
1
a
,
1
.
18
i
i
1
i
i
T
t
λ
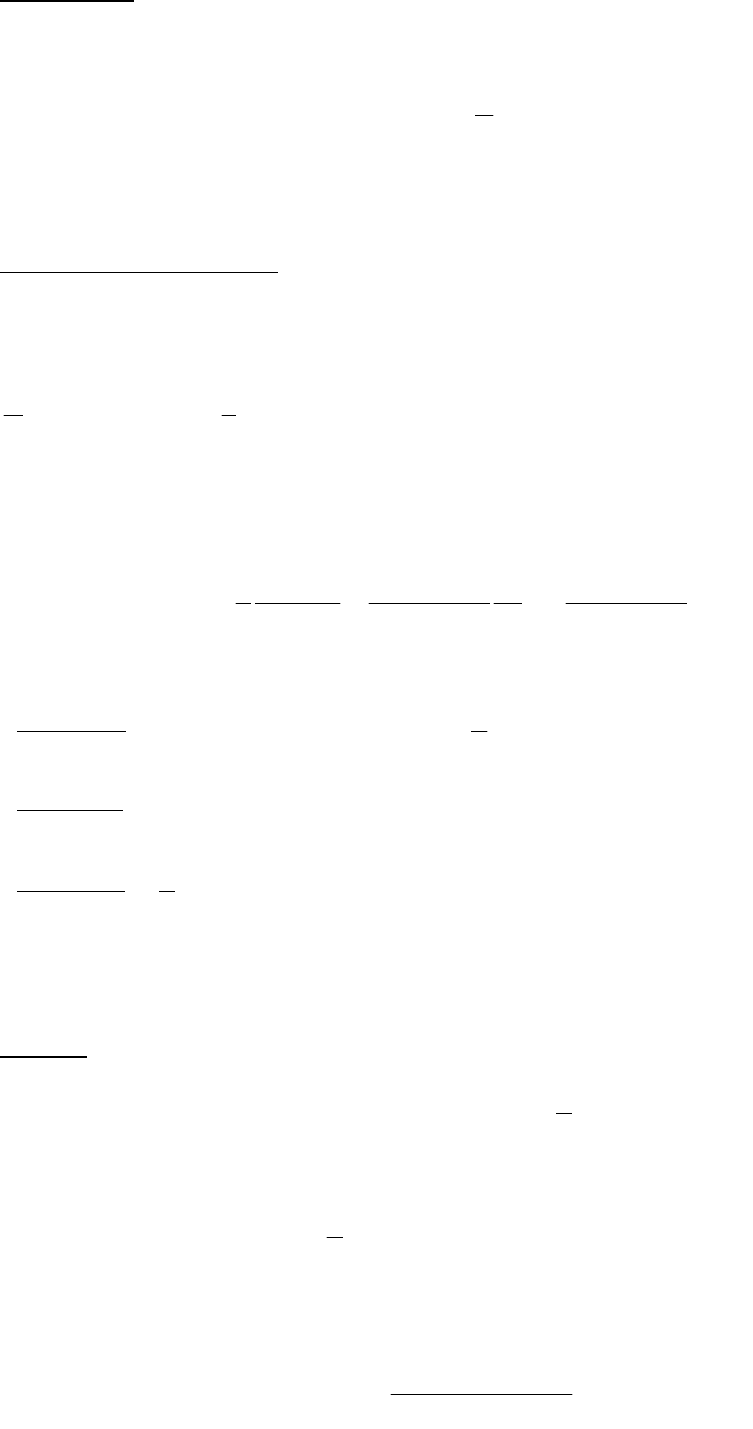
Замечание: система уравнений (2.1) получена аналогично системе уравнений
(1.1). Вероятности переходов для состояний системы совпадают с
точностью до замены
T
t
.
Систему (2.1) будем решать в условиях перегрузки, то есть при
T
.
Первое приближение
В системе уравнений (2.1) произведем замену переменных:
,,,
1
,,,
1
xtiPxit
T
kk
. В результате такой замены производится
переход от дискретной переменной
...,2,1,0i
к непрерывной переменной
0xx
, от t перешли к
, причем
такое, что
10
. После замены
производная равна
,,,,,1 x
t
x
t
tiP
kkk
.
Тогда уравнения (2.1) перепишем
,,,
1
,,,,
,,
210
0
x
a
xx
x
,,,,,,,1
,,
001
1
xxx
x
(2.2)
.,,
,,,,2,,
1,,
2
112
2
x
xxx
a
x
Решим систему уравнений (2.2) в два этапа.
1 этап. Считая
0
и предполагая, что
,,,lim
0
xx
kk
будем иметь
,,
1
,,
210
x
a
xx
,,,1
01
xx
(2.3)
,,
1
12
xx
a
.
Выразим
,x
k
через функцию
2
0
,,
k
k
xx
и получим
,,
12
1
,
2
0
x
GaG
G
x
19
,,
12
,
2
1
x
GaG
G
x
(2.4)
,,
12
,
2
2
2
x
GaG
aG
x
где
,G
,x
асимптотическая плотность распределения
нормированного числа заявок в источнике повторных вызовов.
Обозначим
,
12
,
12
,
12
1
2
2
2
2
1
2
0
GaG
aG
R
GaG
G
R
GaG
G
R
(2.5)
(
k
R
- это асимптотическая вероятность того, что обслуживающий прибор
находится в состоянии k). Заметим, что из системы (2.3) следуют равенства
связывающие
0
R
,
1
R
и
2
R
,
2
10
a
R
RRG
,1
01
RGRG
(2.6)
1
2
RG
a
R
.
Найдем вид функции
,x
, для этого перейдем ко второму этапу.
2 этап . В системе дифференциальных уравнений (2.2) все функции с
аргументом
2, xx
разложим в ряд по приращению аргумента
x
,
ограничиваясь слагаемыми порядка
, получим
,,,
1
,,,,
,,
210
0
x
a
xxG
x
,
,,
,,,,1
,,
0
01
1
x
x
xGxG
x
(2.7)
.
,,
,,
,,
,,
2,,,,
1,,
2
2
1
1
12
2
x
x
x
x
x
x
x
xGx
a
x
20
