Денисенко Н.В., Корзюк А.Ф. Учебно-методическое пособие. Линейная алгебра и математический анализ + примеры решения типовых задач
Подождите немного. Документ загружается.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Белорусский государственный экономический университет
Н.В.Денисенко, А.Ф.Корзюк, И.В.Рыбалтовский, Е.И.Шилкина
ЛИНЕЙНАЯ АЛГЕБРА И МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Учебно-методическое пособие
Для студентов Высшей школы управления и бизнеса
МИНСК 2006
Печатается в авторской редакции
Р е ц е н з е н т доктор физико-математических наук, профессор
И.В.Белько
Р е к о м е н д о в а н о кафедрой высшей математики
У т в е р ж д е н о Научно-методическим советом университета
Линейная алгебра и математический анализ: Учебно-методическое
пособие / Н.В.Денисенко, А.Ф.Корзюк, И.В.Рыбалтовский,
Е.И.Шилкина. – Мн.: БГЭУ, 2006. – 35 с.
© Н.В.Денисенко, А.Ф.Корзюк,
И.В.Рыбалтовский, Е.И.Шилкина, 2006
© Белорусский государственный
экономический университет, 2006
I. ЛИНЕЙНАЯ АЛГЕБРА
1.1. Решение систем линейных неравенств в
2
R
Пусть задано некоторое линейное относительно переменных и
неравенство:
1
x
2
x
bxaxa
≤
+
2211
, (1.1)
где заданные действительные числа.
−baa
,21
,
Решением неравенства называется такая пара действительных чисел
, которые удовлетворяют неравенству (1.1). Если трактовать и
как координаты точек пространства
(
21
, xx
)
1
x
2
x
2
R
, т.е. плоскости , то областью
решений неравенства называется совокупность всех точек плоскости, ко-
ординаты которых удовлетворяют неравенству (1.1). Областью решений
линейного неравенства является одна из полуплоскостей, на которые гра-
ничная прямая
21
xOx
bxaxa
=
+
2211
делит плоскость .
21
xOx
Пусть требуется определить область решений системы m линейных
неравенств вида (1.1):
(1.2)
⎪
⎪
⎭
⎪
⎪
⎬
⎫
≤+
≤+
≤+
.
.......,....................
,
,
2211
2222121
1212111
mmm
bxaxa
bxaxa
bxaxa
Системы вида (1.2) возникают при моделировании многих экономи-
ческих задач. Решением системы (1.2) является пересечение решений каж-
дого из неравенств. Оно представляет собой либо выпуклый многогранник,
либо выпуклую неограниченную область, либо пустое множество точек.
Одной из экономических интерпретацией неравенства (1.1.) является
бюджетное множество, которое определяется как множество наборов то-
варов в количествах и соответственно (первого и второго ви-
да), которые можно приобрести по ценам и за единицу товара, имея
заданную сумму b денежных единиц.
(
21
, xx
)
1
x
2
x
1
a
2
a
Пример 1.1. Построить на плоскости область решений систе-
мы линейных неравенств:
21
xOx
⎪
⎭
⎪
⎬
⎫
≥≥
≥+
≤
+
.0,0
,1
,623
21
21
21
xx
xx
xx
(1.3)
Решение. Построим граничные прямые:
3

()
121
623 lxx =+
;
(
)
221
1 lxx =+
;
(
)
31
9 lx
=
;
(
)
42
0 lx
=
. Прямые и
()
1
l
(
)
2
l
строим по двум точкам, а именно, точкам пересечения с осями координат.
Построим прямую :
()
1
l 623
21
=
+
xx
. Если
0
2
=
x
, то ,
6023
1
=⋅+x 2
1
=
x
,
значит, прямая пересекает ось в точке А (2; 0); если
()
1
l
1
xO 0
1
=
x
, то
, , значит, прямая
6203
2
=+⋅ x 3
2
=x
(
)
1
l
пересекает ось в точке
2
xO
В (0; 3). Аналогично устанавливаем, что прямая
(
)
2
l
пересекает оси и
в точках С (1; 0) и D (0; 1) соответственно. Прямые и задают
уравнения осей координат и соответственно.
1
xO
2
xO
()
3
l
()
4
l
2
xO
1
xO
Каждая из построенных прямых разбивает плоскость на две полу-
плоскости, одна из которых (ее направление укажем стрелкой) является
решением неравенства, соответствующего граничной прямой. Для того,
чтобы узнать, какая именно из двух полуплоскостей является решением
неравенства, в неравенство, соответствующее рассматриваемой граничной
прямой, подставим координаты точки, не лежащей на этой прямой, напри-
мер, для и подставим точку О (0; 0): ,
()
1
l
()
2
l
60203 ≤⋅+⋅
(
)
1
l
;
, . Получим числовые неравенства
10101 ≤⋅+⋅
()
2
l
60
≤
, которое является
истинным, следовательно, стрелка направлена от прямой в полуплос-
кость с точкой О (0; 0) и 1, которое является ложным, следовательно,
стрелка направлена от прямой
()
1
l
0 ≥
(
)
2
l
в полуплоскость, не содержащую точку
О (0; 0). Неравенство задает полуплоскость, лежащую правее прямой
; а неравенство задает полуплоскость, лежащую выше прямой
. Пересечение отмеченных полуплоскостей (четырехугольник АСDВ) и
есть область решений системы неравенств (1.3):
0
1
≥x
()
1
l 0
2
≥x
()
2
l
2
x
1
x
()
3
l
()
1
l
(
)
4
l
()
2
l
В
D
А С
3
2
1
0 1 2 3
Рис. 1.1.
4

1.2. Задача 1 для контрольной работы
Построить на плоскости область решений системы линейных
неравенств:
21
xOx
1.1. 1.2.
⎪
⎩
⎪
⎨
⎧
≥≥
≤+
≤−
.0,0
,84
,62
21
21
21
xx
xx
xx
⎪
⎩
⎪
⎨
⎧
≥≥
≤+
≤
+
.0,0
,63
,63
21
21
21
xx
xx
xx
1.3. 1.4.
⎪
⎩
⎪
⎨
⎧
≥≥
≤+
≤+
.0,0
,8
,122
21
21
21
xx
xx
xx
⎪
⎩
⎪
⎨
⎧
≥≥
≥+
≤
+
.0,0
,62
,12
21
21
21
xx
xx
xx
1.5. 1.6.
⎪
⎩
⎪
⎨
⎧
≥≥
≥+
≤+
.0,0
,2
,632
21
21
21
xx
xx
xx
⎪
⎩
⎪
⎨
⎧
≥≥
≥+
≤
+
.0,0
,1
,1243
21
21
21
xx
xx
xx
1.7. 1.8.
⎪
⎩
⎪
⎨
⎧
≥≥
≥+
≤+
.0,0
,42
,63
21
21
21
xx
xx
xx
⎪
⎩
⎪
⎨
⎧
≥≥
≥+
≤
+
.0,0
,3
,1052
21
21
21
xx
xx
xx
1.9. 1.10.
⎪
⎩
⎪
⎨
⎧
≥≥
≥+
≤+
.0,0
,62
,10
21
21
21
xx
xx
xx
⎪
⎩
⎪
⎨
⎧
≥≥
≥+
≤
+
.0,0
,3
,84
21
21
21
xx
xx
xx
1.3. Решение систем линейных уравнений матричным методом
Пусть задана система n линейных уравнений с n неизвестными:
(1.4)
⎪
⎪
⎭
⎪
⎪
⎬
⎫
=+++
=+++
=+++
.
,........................................
,
,
2211
22222112
11212111
nnnnnn
nn
nn
bxaxaxa
bxaxaxa
bxaxaxa
…
…
…
Матрица
()
njniaA
ij
,1;,1, ===
, называется матрицей системы (1.4). Ес-
ли ее определитель
A
de
t
=Δ отличен от нуля, то система (1.4) имеет един-
ственное решение
, (1.5)
BAX
1−
=
5

где матрица-столбец неизвестных,
(
−
′
=
n
xxxX ,,,
21
…
)
()
−
′
=
n
bbbB ,,,
21
…
матрица-столбец свободных членов;
−
−1
A
матрица, обратная матрице А,
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
Δ
=
−
nnnn
n
n
AAA
AAA
AAA
A
…
…………
…
…
21
22212
12111
1
1
, (1.6)
()
−−=
+
ij
ji
ij
MA 1 алгебраические дополнения элементов матрицы А,
определитель (
n – 1)-го порядка, полученный из матрицы А вычерки-
ванием
i-ой строки и j-го столбца.
ij
a
−
ij
M
Рассмотрим экономическую иллюстрацию системы (1.4). Если пред-
приятие из m видов ресурсов , имеющихся в количествах
производит
n видов продукции и
норма расхода
i-го ресурса на производство единицы продукции j-го
вида, то матрица
mi
PPPP ,,,,,
21
……
mi
bbbb ,,,,,
21
……
nj
ПППП ,,,,,
21
……
−
ij
a
()
njmiaA
ij
,1;,1, ===
с неотрицательными элементами
называется
матрицей норм расхода или технологической матрицей.
Тогда, если запланировать к производству по единиц
продукции , то произведение
i-ой строки матрицы А
на матрицу-столбец
Х, равное
ij
a
nj
xxxx ,,,,,
21
……
nj
ПППП ,,,,,
21
……
ninjijii
xaxaxaxa +
+
+
+
+
……
2211
равно рас-
ходу
i-го ресурса на производство плана Х. Предполагая полное использо-
вание всех ресурсов и равенство
m = n, получаем, что для поиска такого
плана производства надо решить систему (1.4).
Пример 1.2. Пусть для производства трех видов продукции
расходуется три вида ресурсов , имеющихся в количе-
ствах единиц соответственно. Норма расхода ресурсов
3
ППП ,,
21 3
PPP ,,
21
321
,, bbb
(
)
ij
a , их
количества представлены таблицей:
Таблица 1.1.
Требуется записать в математической форме условия, которым дол-
жен удовлетворять план выпуска продукции каждого вида, при
321
,, xxx
j
П
i
P
1
П
2
П
3
П
1
P
2
P
3
P
1
2
2
1
3
1
1
4
3
9
13
11
Запасы
()
i
b
6
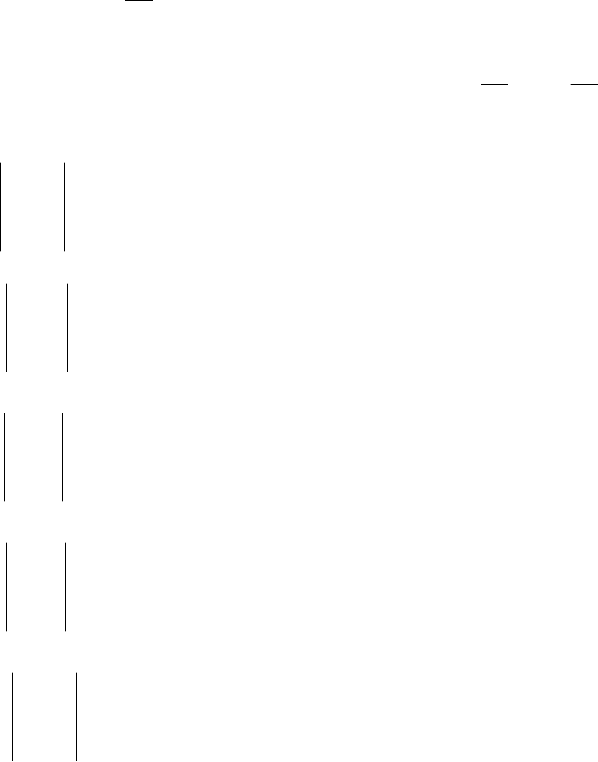
условии, что предполагается полное использование всех ресурсов и найти
этот план.
Решение. Составляем систему уравнений
⎪
⎩
⎪
⎨
⎧
=++
=++
=++
.1132
,1343
,92
321
321
321
xxx
xxx
xxx
Матрица . Находим ее определитель по правилу треугольни-
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
312
431
112
A
ка: Δ = 2 · 3 · 3 + 1 · 1 · 1 + 1 · 4 · 2 – 2 · 3 · 1 – 1 · 1 · 3 – 1 · 4 · 2 = 18 + 1 + 8 –
– 6 – 3 – 8 = 10. Поскольку Δ = 10 ≠ 0, то обратная матрица
1−
A
существует
и, согласно (1.6), имеет вид:
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
−
332313
322212
312111
1
10
1
AAA
AAA
AAA
A
, (1.7)
Находим алгебраические дополнения
(
)
ij
ji
ij
MA
+
−= 1, 3,1;3,1 == ji . Име-
ем:
()
54133
31
43
1
11
11
11
=⋅−⋅=+=−=
+
MA
;
() ()
583
32
41
1
12
21
12
=−−=−=−=
+
MA
;
()
561
12
31
1
13
31
13
−=−=+=−=
+
MA
;
() ()
213
31
11
1
21
12
21
−=−−=−=−=
+
MA
;
()
426
32
12
1
22
22
22
=−=+=−=
+
MA
;
7
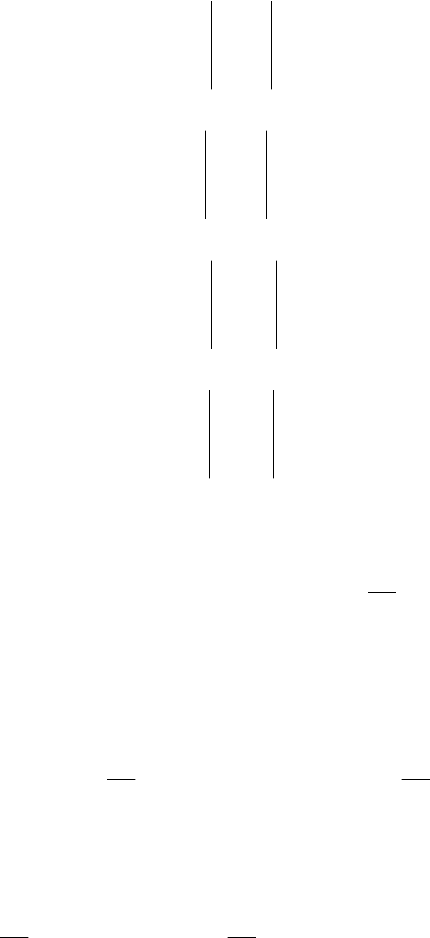
() ()
022
12
12
1
23
32
23
=−−=−=−=
+
MA
;
()
11341
43
11
1
31
13
31
=⋅−⋅=+=−=
+
MA
;
() ()
71142
41
12
1
32
23
32
−=⋅−⋅−=−=−=
+
MA
;
()
51132
31
12
1
33
33
33
=⋅−⋅=+=−=
+
MA
.
Тогда, по (1.7), имеем:
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
=
−
505
745
125
10
1
1
A
,
значит, по (1.5)
(
)
()
()
.
1
2
3
10
20
30
10
1
55045
775245
112645
10
1
11513095
11713495
11113295
10
1
11
13
9
505
745
125
10
1
3
2
1
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
++−
−+
+−
=
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅+⋅+⋅−
⋅−+⋅+⋅
⋅+⋅−+⋅
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
x
x
x
X
Ответ: надо запланировать к производству
3
1
=
x
единицы продукции
единицы продукции и
2,
11
=xП
2
П 1
3
=
x
единицу продукции вида .
3
П
1. 4. Задача 2 для контрольной работы
Предприятие выпускает три вида продукции , расходуя при
этом ресурсы , имеющиеся в количествах единиц соответст-
321
,, ППП
321
,, PPP
321
,, bbb
8

венно. Нормы расхода ресурса на производство единицы продукции
заданы матрицей
i
P
j
П
()
3,1,3,1, === iiaA
ij
. Предполагая полное использование
ресурсов, записать в математической форме условия, которым должен удов-
летворять план выпуска продукции каждого вида соответственно и
решить полученную систему уравнений любым из известных методов реше-
ния систем линейных алгебраических уравнений.
321
,, xxx
2.1. . 2.2. .
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
8
13
7
,
311
254
132
BA
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
17
20
21
,
215
143
217
BA
2.3. . 2.4. .
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
13
12
8
,
243
432
321
BA
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
9
8
5
,
213
312
211
BA
2.5. . 2.6. .
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
11
9
8
,
321
123
212
BA
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
10
19
27
,
211
323
515
BA
2.7. . 2.8. .
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
16
24
14
,
513
254
151
BA
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
18
19
13
,
421
213
112
BA
2.9. . 2.10. .
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
19
10
29
,
213
121
215
BA
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
17
11
14
,
413
221
321
BA
9

II. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
2.1. Предел функции
Число а называется пределом последовательности ,
если для любого существует целое положительное число N
, зависящее от
ε, такое, что для всех членов последовательности с номерами
…… ,,,,,
n321
xxxx
0>ε
N
n ≥ выполня-
ется неравенство
ε<− ax
n
. Предел обозначается
n
n
xa
∞→
=
lim .
Последовательность, имеющая предел, называется
сходящейся, в про-
тивном случае –
расходящейся.
Число
А называется пределом функции f (x) в точке (или при
), если для любой, сходящейся к последовательности
значений аргумента, отличных от , соответствующая по-
следовательность
0
x
0
xx →
0
x
…… ,,,,,
321 n
xxxx
0
x
() ()
(
)
(
)
…… ,,,,,
321 n
xfxfxfxf
значений функции сходится
к числу
А. Предел обозначается
(
)
xfA
xx
0
lim
→
=
.
Приведем основные теоремы, на которых основано вычисление преде-
лов:
1.
Если существуют
(
)
xf
xx
1
0
lim
→
и
(
)
xf
xx
2
0
lim
→
, то
а)
() ()()
(
)
(
)
xfxfxfxf
xxxxxx
2121
000
limlimlim
→→→
+
=± ;
б)
() () ()
(
)
xfxfxfxf
xxxxxx
2121
000
limlimlim
→→→
⋅
=⋅ ;
в)
()
()
()
()
xf
xf
xf
xf
xx
xx
xx
2
1
2
1
0
0
0
lim
lim
lim
→
→
→
= (при условии
(
)
0lim
2
0
≠
→
xf
xx
.
2. Для всех основных элементарных функций в любой точке их области
определения имеет место равенство .
() ( )
0
00
limlim xfxfxf
xxxx
=
⎟
⎠
⎞
⎜
⎝
⎛
=
→→
3. Первый замечательный предел:
1
sin
lim
0
=
→
x
x
x
.
4. Второй замечательный предел:
e
x
x
x
=
⎟
⎠
⎞
⎜
⎝
⎛
+
∞→
1
1lim
,
()
ex
x
x
=+
−
→
1
0
1lim
.
10
