Денисенко Н.В., Корзюк А.Ф. Учебно-методическое пособие. Линейная алгебра и математический анализ + примеры решения типовых задач
Подождите немного. Документ загружается.

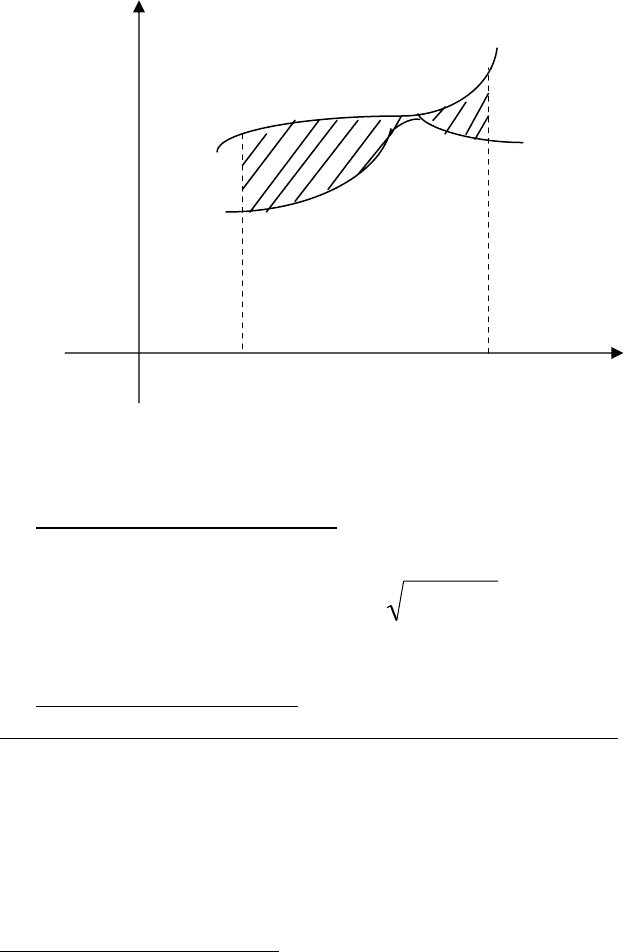
() ()()
∫
−=
b
a
dxxyxyS
12
,
у
х
0
а b
2
A
1
A
2
B
1
B
Рис. 2.1
2.
Вычисление длины дуги.
Длина дуги отрезка гладкой кривой у = у (х)
(
)
bxa
≤
≤
равна
()
∫
′
+=
b
a
2
dxy1l .
3.
Вычисление объемов.
Объем тела по известным поперечным сечениям. Если объем V тела
существует и
() ( )
bxaxSS
≤
≤
=
есть площадь сечения тела плоскостью,
перпендикулярной к оси Ох в точке х, то
()
∫
=
b
a
dxxSV .
Объем тела вращения. Объем тела, образованного вращением вокруг
оси 0х площади
()
(
)
xyybxa
≤
≤
≤≤ 0,
, где у (х) – непрерывная однозначная
функция, равен
()
∫
π=
b
a
2
x
dxxyV .
21

Пример 2.7. Найти площадь фигуры, ограниченной линиями
36
2
+−= xxy и у = х + 3.
Решение. Найдем точки пересечения параболы и прямой
у = х + 3. Для этого решим систему
36
2
+−= xxy
.
3
;07
,
3
;363
,
3
;36
222
⎩
⎨
⎧
+=
=−
⎩
⎨
⎧
+=
+−=+
⎩
⎨
⎧
+=
+−=
xy
xx
xy
xxx
xy
xxy
Отсюда , , ,
0
1
=x 7
2
=x 0
1
=y 10
2
=
y
, а точки пересечения А (0; 3), В (7; 10).
Построим чертеж и найдем пределы интегрирования:
у
х
36
2
+−= xxy
у = х + 3
0 7
3
– 6
Рис. 2.2
Так как
а = 0, b = 7,
()
3
+
= xxf
,
(
)
36
2
+−=ϕ xxx
, то искомая площадь равна:
()()() ()
()()(())
.).ед .(кв
6
1
57
6
343
3
7
2
7
0
7
32
7
7363
3332
7
0
2
7
0
2
==⋅=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
=−=+−−+=ϕ−=
∫∫∫
xx
dxxxdxxxxdxxxfS
b
a
Пример 2.8.
Найти объем тела, образованного вращением вокруг оси 0х
фигуры, ограниченной линиями и
у = х.
2
xy =
22

Решение. Решим систему уравнений получим ,
⎩
⎨
⎧
=
=
,
,
2
xy
xy
0
1
=x 1
2
=
x
,
, , откуда точки пересечения кривых
0 (0; 0), А (1; 1). Из рис. 2.3
видно, что искомый объем равен разности двух объемов, образованных вра-
щением вокруг оси 0
х треугольника ОАВ и криволинейной трапеции 0mАВ:
0
1
=y 1
2
=y
у
х
0
m
В
А
Рис. 2.3
15
2
5
1
3
1
0
1
53
53
1
0
4
1
0
2
21
π
=
⎟
⎠
⎞
⎜
⎝
⎛
−π=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−π=π−π=−=
∫∫
xx
dxxdxxVVV
(куб. ед.).
2.6. Задача 5 для контрольной работы
Вычислить площадь фигуры, ограниченной линиями (сделать чертеж).
5.1. 7, 6
2
+−= xxy 1
+
=
x
y . 5.2. , 76
2
++= xxy
x
1
=
−
+
y .
5.3. 1, 4
2
+−= xxy 1
+
=
x
y . 5.4. 7, 6
2
++= xxy 7
+
=
x
y .
5.5. , 76
2
+−= xxy . 7
+
−=
x
y
23

Вычислить объем тела, образованного вращением вокруг оси 0
х фигу-
ры, ограниченной линиями.
5.6. , . 5.7.
2
xy = xy =
2
x
y
2
=
, 3
=
x
, 12=
x
, 0
=
y .
5.8.
2
2
1
xy =
, 5,1+−=
x
y . 5.9.
2
2
1
xy =
,
x
y 2
=
.
5.10. , .
2
4 xy −= 0=y
2.7. Дифференциальные уравнения
Уравнение
(
)
0,,
=
′
yyxF
, (2.2)
где
х – аргумент, у (х) – искомая функция,
(
)
−
′
xy
ее производная, называется
дифференциальным уравнением первого порядка, не разрешенным от-
носительно
. Уравнение
y
′
(
)
yxfy ,
=
′
называется дифференциальным
уравнением первого порядка, разрешенным относительно .
y
′
Уравнение
(
)
(
)
0,,
=
+
dyyxQdxyxP
, (2.3)
где
х и у имеют тот же смысл, что и выше; dx, dy – соответственно дифферен-
циалы аргумента и функции, называется
уравнением, записанным в диф-
ференциалах
. В уравнении (2.3) можно у принять за аргумент, х (у) – за
функцию.
Решением уравнений (2.2) и (2.3) в некотором интервале (а, b) изме-
нения независимой переменной называется функция
()
xy ϕ
=
, определенная и
непрерывно дифференцируемая в этом интервале и обращающая эти уравне-
ния в тождества.
Задача нахождения решения, удовлетворяющего заданному начальному
условию , называется
задачей Коши.
(
xx yy
00
при ==
)
)
Функция называется
общим решением дифференциально-
го уравнения
, если:
(
cxy ,ϕ=
1)
для любых
G
C
∈ , где G – некоторая область,
(
)
cxy ,
ϕ
=
является решени-
ем;
2)
для любых из соответствующей области существует , такое,
что .
00
, yx GC ∈
0
()
000
, cxy ϕ=
24
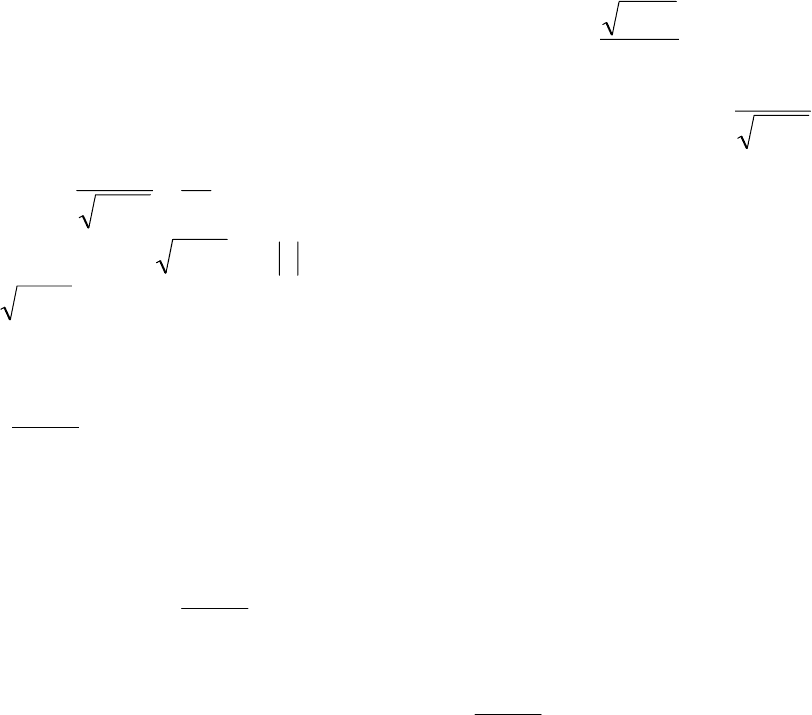
Решение называется частным решением.
(
0
, cxy ϕ=
)
Решение, в каждой точке которого нарушается единственность решения
задачи Коши, называется
особым. Особое решение не содержится в формуле
общего решения ни при каком числовом значении произвольной постоянной.
Если общее решение дифференциального уравнения задано в неявном
виде или
()
0,, =Φ cyx
()
cyx
=
ψ ,
, то оно называется общим интегралом этого
уравнения.
Дифференциальное уравнение
()
(
)
(
)
(
)
0
=
+
dyyQxPdxyNxM
, (2.4)
называется уравнением с разделяющимися переменными.
Уравнение вида
(
)
(
)
xqyxpy
=
+
′
, (2.5)
называется линейным дифференциальным уравнением.
Более подробно с этим разделом можно ознакомиться в учебнике [1] на
стр. 277 – 312.
Пример 2.9. Проинтегрировать уравнение
x
1y
y
−
=
′
.
Решение. Умножим обе части исходного уравнения на
1−y
dx
, тогда
получим
x
dx
y
dy
=
−1
. Проинтегрировав полученное уравнение, получим об-
щий интеграл
cxy =−− ln12
в области ,,1 +∞<
<
∞
−
≥
x
y
(
)
−
∞
+
∞
= ,G
.
Из
01 =−y
, имеем у = 1. Решение у = 1 является особым решением.
Пример 2.10. Найти общее решение дифференциального уравнения
x
x
xy
y =
+
−
′
2
1
2
и частное решение, удовлетворяющее начальному условию
при .
5
0
=y 0
0
=x
Решение. Положим u
v
y
=
, тогда
vuvuy
′
+
′
=
′
и данное уравнение при-
мет вид
x
x
xuv
vuvu =
+
−
′
+
′
2
1
2
,
или
x
x
xv
vuvu =
⎟
⎠
⎞
⎜
⎝
⎛
+
−
′
+
′
2
1
2
(*).
25

Выберем функцию так, чтобы выражение в скобках, т.е. сумма
()
xvv =
2
1
2
x
xv
v
+
−
′
было равно нулю. Такой функцией может быть любое частное ре-
шение уравнения
0
1
2
2
=
+
−
′
x
xv
v
. Решим это уравнение
2
1
2
x
xv
dx
dv
+
=
;
2
1
2
x
x
v
dv
+
=
;
∫∫
+
=
2
1 x
dxx
v
dv
;
(
)
2
1lnln xv +=
;
2
1
x
v
+
= .
Подставив в уравнение (*) найденное значение
v, получим
(
)
xxu =+
′
2
1
, от-
сюда
2
1 x
x
dx
du
+
=
;
2
1 x
dxx
du
+
=
;
∫∫
+
=
2
1 x
dxx
du
;
()
cxu ++=
2
1ln
2
1
. Следова-
тельно, общее решение данного уравнения будет
()()
22
11ln
2
1
xcxy +
⎟
⎠
⎞
⎜
⎝
⎛
++=
.
Найдем частное решение, удовлетворяющее начальному условию. Ес-
ли при , то
5
0
=y 0
0
=x
() (
0101ln
2
1
5 +⋅
⎟
⎠
⎞
⎜
⎝
⎛
++= c
)
; с = 5.
Таким образом,
()
()
2
151ln
2
1
xxy +
⎟
⎠
⎞
⎜
⎝
⎛
++=
есть частное решение, удовлетворяющее заданным начальным условиям.
2.8. Задача 6 для контрольной работы
Найти общее решение дифференциального уравнения и частное реше-
ние, удовлетворяющее начальному условию
o
yy
=
при .
0
xx =
6.1.
x
ytgxy
cos
1
=+
′
;
1
0
=
y
,
0
0
=
x
.
6.2.
2
2
x
x
y
y =−
′
; ,
0
0
=y 1
0
=
x
.
6.3.
2
2
−
=+
′
x
x
y
y ; ,
1
0
=y 3
0
=
x
.
26
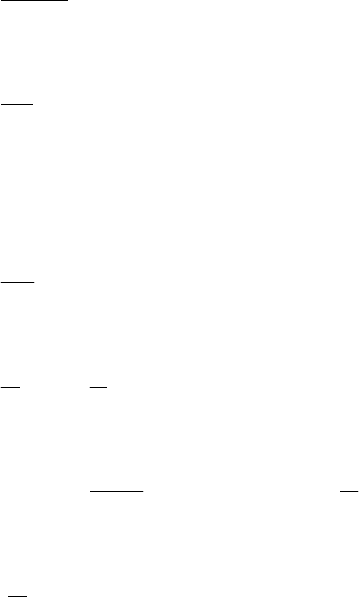
6.4.
2
2
1
1
2
x
x
xy
y +=
+
−
′
;
0
0
=
y
,
0
0
=
x
.
6.5.
4
2
3
x
x
y
y =−
′
; ,
3
0
=y 1
0
=
x
.
6.6. ; ,
x
eyy =−
′
2
0
=y 0
0
=
x
.
6.7. 32
4
−=−
′
x
x
y
y
;
1
0
=
y
,
1
0
=
x
.
6.8.
xx
y
y
1
2 +=−
′
; ,
2
0
=y 1
0
=
x
.
6.9.
x
yctgxy
sin
1
=−
′
;
3
0
=
y
,
2
0
π
=x
.
6.10. x
x
y
y 3=−
′
; ,
5
0
=y 1
0
=
x
.
2.9. Ряды
Числовым рядом называется выражение
, (2.6)
∑
∞
=
=++++
1
21
n
nn
aaaa ……
где числа называемые
членами ряда, образуют числовую
последовательность;
…… ,,,,
21 n
aaa
(
)
nfa
n
=
называется общим или n-м членом. Сумма
конечного числа
n первых членов ряда (2.6) называется его n-й частичной
суммой: .
nn
aaaS +++= …
21
Ряд (1) называется
сходящимся, если последовательность
{
}
n
S
его
частичных сумм сходится к числу
S, которое называется суммой этого ряда,
т.е. если
SS
n
n
=
∞→
lim .
Если не существует или равен бесконечности, то ряд назы-
вается
расходящимся.
SS
n
n
=
∞→
lim
Сходимость (расходимость) положительных рядов исследуется с по-
мощью признаков сравнения ([1], стр. 318 – 320), признака Д’Аламбера ([1],
стр. 320 – 321), признака Коши ([1], стр. 322), интегрального признака ([1],
стр. 322 – 324).
27

Знакопеременный ряд, у которого любые два соседних члена имеют
разные знаки, называется
знакочередующимся. Сходимость знакочере-
дующегося ряда определяется по признаку Лейбница ([1], стр. 327 – 328).
Степенным рядом называется функциональный ряд вида
, (2.7)
n
n
n
n
n
xaxaxaxaa
∑
∞
=
=+++++
0
2
210
……
где действительные числа, называемые
коэффициентами
ряда.
−…… ,,,,
10 n
aaa
Степенной ряд вида
, (2.8)
()() (
n
n
n
n
n
xxaxaxxaxxaa
0
0
2
02010
−=+++−+−+
∑
∞
=
……
)
можно свести к ряду (2.7) если сделать замену
yxx
=
−
0
.
Радиусом сходимости степенного ряда (2.7) называется неотрицатель-
ное число
R, что при Rx < ряд сходится, при Rx > расходится. Интервал
(–
R, R) называется интервалом сходимости ряда.
Радиус сходимости ряда (2) можно вычислить по одной из следующих
формул:
1
lim
+
∞→
=
n
n
n
a
a
R
,
n
n
n
a
R
∞→
=
lim
1
.
На концах интервала сходимости, т.е. при
х = – R, х = R, ряд (2.7) мо-
жет либо сходиться, либо расходиться. Этот вопрос решается для каждого
конкретного ряда отдельно.
Пример 2.11. Написать три первых члена по заданному общему члену
; написать радиус, интервал и область сходимости степенного ряда
n
n
xa
∑
∞
=1
2
n
nn
n
x
.
Решение. …+++=
∑
∞
=
32
1
3
8
2
4
2
2
xxx
n
x
n
nn
. Найдем радиус сходимо-
сти данного ряда. Так как
n
a
n
n
2
=
,
1
2
1
1
+
=
+
+
n
a
n
n
, то
2
11
1
2
1
lim
1
2
1
lim
2
12
limlim
1
1
=+=
+
=
+
⋅==
∞→∞→
+
∞→
+
∞→
nn
nn
n
a
a
R
nn
n
n
n
n
n
n
. Следовательно,
28
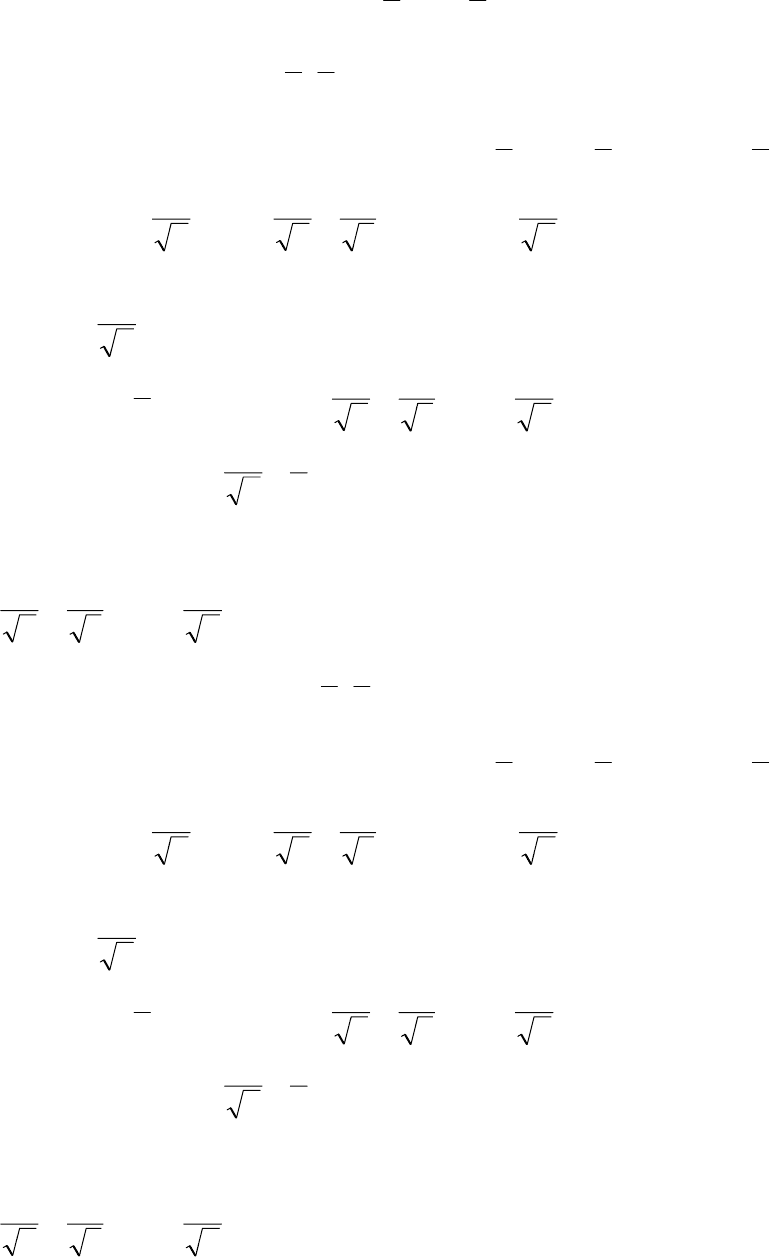
интервал сходимости имеет вид
2
1
2
1
<<− x
. Это означает, что ряд сходится
абсолютно при всех
⎟
⎠
⎞
⎜
⎝
⎛
−∈
2
1
;
2
1
x , а вне этого интервала он расходится.
Исследуем сходимость ряда при
2
1
−=x
и
2
1
=x
. При
2
1
−=x
ряд име-
ет вид
() ()
…… +−++−+−=−
∑
∞
=
nn
n
n
n
1
1
3
1
2
1
1
1
1
1
. Это знакочередую-
щийся ряд, члены которого убывают по абсолютной величине при
∞
→n и
n
a
n
n
n
1
limlim
∞→∞→
=
. Согласно признака Лейбница это ряд сходится.
При
2
1
=x
имеем ряд
…… +++++
n
1
3
1
2
1
1
.
Очевидно, что
n
n
11
≥
(
)
…,3,2,1
=
n
, т.е. каждый член данного ряда
больше соответствующего члена расходящегося гармонического ряда или
равен ему. Следовательно, по признаку сравнения ряд
…… +++++
n
1
3
1
2
1
1
расходится. Следовательно, областью сходимости
ряда является промежуток
⎟
⎠
⎞
⎢
⎣
⎡
−
2
1
;
2
1
.
Исследуем сходимость ряда при
2
1
−=x
и
2
1
=x
. При
2
1
−=x
ряд име-
ет вид
() ()
…… +−++−+−=−
∑
∞
=
nn
n
n
n
1
1
3
1
2
1
1
1
1
1
. Это знакочередую-
щийся ряд, члены которого убывают по абсолютной величине при
∞
→n и
n
a
n
n
n
1
limlim
∞→∞→
=
. Согласно признака Лейбница это ряд сходится.
При
2
1
=x
имеем ряд
…… +++++
n
1
3
1
2
1
1
.
Очевидно, что
n
n
11
≥
(
)
…,3,2,1
=
n
, т.е. каждый член данного ряда
больше соответствующего члена расходящегося гармонического ряда или
равен ему. Следовательно, по признаку сравнения ряд
…… +++++
n
1
3
1
2
1
1
расходится. Следовательно, областью сходимости
29
ряда является промежуток
⎟
⎠
⎞
⎢
⎣
⎡
−
2
1
;
2
1
.
2.10. Задача 7 для контрольной работы
Записать три первых члена, найти радиус, интервал и область
сходимости степенного ряда:
7.1.
()
∑
∞
=
+
1
2
1
n
n
n
x
. 7.2.
(
)
∑
∞
=
−
1
1
n
n
n
n
x
.
7.3.
()( )
∑
∞
=
−
−−
1
3
1
21
n
nn
n
x
. 7.4.
(
)
∑
∞
=
−
1
3
3
n
n
n
x
.
7.5.
()
∑
∞
=
−
1
2
1
n
n
n
n
x
. 7.6.
∑
∞
=
+
1
2
n
n
n
nx
.
7.7.
∑
∞
=1
2
2
n
nn
n
x
. 7.8.
∑
∞
=1
3
n
n
n
x
.
7.9.
∑
∞
=1
3
n
nn
n
x
. 7.10.
(
)
∑
∞
=
−
1
1
n
n
n
n
x
.
30
