Денисенко Н.В., Корзюк А.Ф. Учебно-методическое пособие. Линейная алгебра и математический анализ + примеры решения типовых задач
Подождите немного. Документ загружается.


Говорят, что отношение двух функций
(
)
()
xf
xf
2
1
является неопределенно-
стью вида
0
0
, если при и
()
0
1
→xf
0
xx →
(
)
0
2
→xf
при . Аналогично
определяются неопределенности видов:
0
xx →
00
,0,1,0,, ∞∞⋅∞−∞
∞
∞
∞
.
Пример 2.1. Найти
2
972
lim
2
2
−+
−+
→
x
x
xx
cx
, если а) с = 2; б) с = 1; в) с = ∞.
Решение. а) Применяя теорему о пределе частного, получим
(
)
()
4
13
222
92722
2lim
972lim
2
972
lim
2
2
2
2
2
2
2
2
2
=
−+
−⋅+⋅
=
−+
−+
=
−+
−+
→
→
→
xx
xx
xx
xx
x
x
x
;
Ответ:
4
13
.
б)
2
972
lim
2
2
1
−+
−+
→
x
x
xx
x
. Здесь предел знаменателя равен нулю, следователь-
но, теорему о пределе частного применить нельзя. Предел числителя тоже ра-
вен нулю. Имеем неопределенность вида
0
0
. Для того, чтобы раскрыть эту не-
определенность, разложим числитель и знаменатель на множители. Таким
образом,
()
()( )
3
11
21
912
2
92
lim
2
2
9
2
lim
21
2
9
12
lim
2
972
lim
111
2
2
1
=
+
+⋅
=
+
+
=
+
⎟
⎠
⎞
⎜
⎝
⎛
+
=
+−
⎟
⎠
⎞
⎜
⎝
⎛
+−
=
−+
−+
→→→→
x
x
x
x
xx
xx
xx
xx
xxxx
.
Ответ:
3
11
.
в)
2
972
lim
2
2
−+
−+
∞→
x
x
xx
x
. Здесь числитель и знаменатель при ∞→
x
стремят-
ся к бесконечности, поэтому теорему о пределе частного применить нельзя.
Преобразовав аналитическое выражение под знаком предела и разделив чис-
литель и знаменатель на
2
x
, получим:
2
001
002
21
1
97
2
lim
2
972
lim
2
2
2
2
=
−+
−+
=
−+
−+
=
−+
−+
∞→∞→
x
x
xx
xx
xx
xx
. Ответ: 2.
11

Пример 2.2. Найти
xtg
x
x
5
3sin
lim
0→
.
Решение. Здесь мы имеем неопределенность вида
0
0
. Преобразуем
функцию
xtg
x
5
3sin
таким образом, чтобы использовать первый замечательный
предел
⎟
⎠
⎞
⎜
⎝
⎛
=
α
α
→α
1
sin
lim
0
:
5
3
1
51
11
5cos
5
5
5sin
3
3
3sin
lim5cos
5sin
3sin
lim
5
3sin
lim
000
=⋅
⋅
⋅
=
⋅
⋅
==
→→→
x
x
x
x
x
x
x
x
xtg
x
xxx
.
Ответ:
5
3
.
Пример 2.3. Найти
25
2
lim
+
∞→
⎟
⎠
⎞
⎜
⎝
⎛
+
n
x
n
n
.
Решение. В этом примере неопределенность вида , так как
∞
1
1
2
1lim
2
lim =
⎟
⎠
⎞
⎜
⎝
⎛
+=
+
∞→∞→
nn
n
nn
, а
(
)
∞
=
+
∞→
25lim n
n
. Преобразуем данное выражение
так, чтобы использовать второй замечательный предел
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
+
∞→
e
x
x
x
1
1lim
:
()
.
2
1lim
2
1lim
2
1lim
2
1lim
2
lim
10
4
10
2
410
2
25
2
2
2525
e
n
nnnn
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+=
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+=
⎟
⎠
⎞
⎜
⎝
⎛
+=
⎟
⎠
⎞
⎜
⎝
⎛
+
+
∞→
+
∞→
+⋅
∞→
+
∞→
+
∞→
Ответ: .
10
e
12

2.2. Задача 3 для контрольной работы
Найти пределы функций, не применяя правило Лопиталя.
3.1. 1)
4
65
lim
2
2
−
+−
→
x
xx
cx
, если а) с = 1; б) с = 2; в) с = ∞;
2)
2
sin
3sin
lim
0
x
x
x→
; 3)
x
x
x
2
3
1lim
⎟
⎠
⎞
⎜
⎝
⎛
+
∞→
.
3.2. 1)
65
252
lim
2
2
+−
+−
→
x
x
xx
cx
, если а) с = 1; б) с = 2; в) с = ∞;
2)
x
xtg
x
2sin
3
lim
0→
; 3)
()
x
x
x
1
0
31lim +
→
.
3.3. 1)
352
1543
lim
2
2
−−
−−
→
x
x
xx
cx
, если а) с = 1; б) с = 3; в) с = ∞;
2)
2
sin
3sin
lim
0
x
x
x→
; 3)
x
x
x
2
3
1lim
⎟
⎠
⎞
⎜
⎝
⎛
+
∞→
.
3.4. 1)
352
25
lim
2
2
−+
−
→
x
x
x
cx
, если а) с = 6; б) с = 5; в) с = ∞;
2)
xtg
x
x
4
8sin
lim
0→
; 3)
()
x
x
x
3
1
0
21lim −
→
.
3.5. 1)
472
8143
lim
2
2
−−
+−
→
x
x
xx
cx
, если а) с = 2; б) с = 4; в) с = ∞;
2) ; 3) xctgx
x
28sinlim
0
⋅
→
n
n
n
n
3
1
lim
⎟
⎠
⎞
⎜
⎝
⎛
+
∞→
.
13
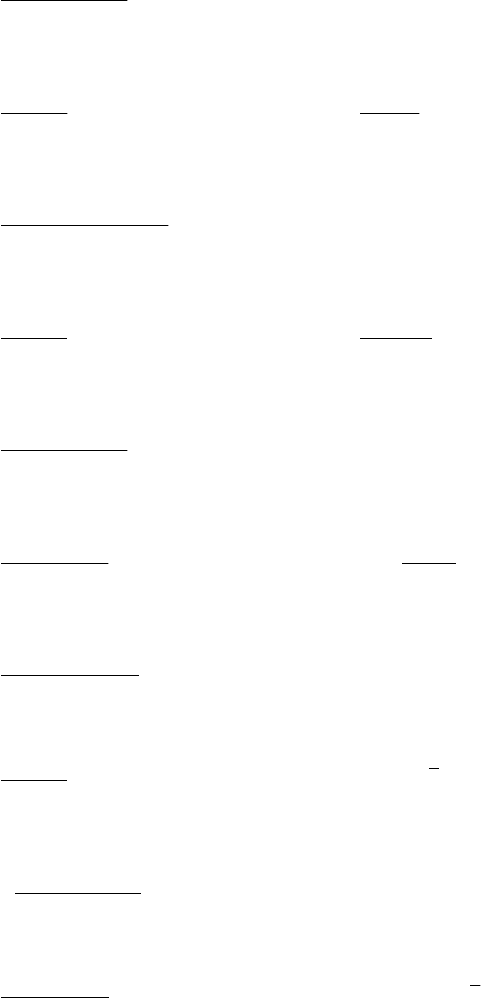
3.6. 1)
1
32
lim
2
2
−
−+
→
x
xx
cx
, если а) с = 2; б) с = 1; в) с = ∞;
2)
x
xtg
x
5sin
3
lim
0→
; 3)
53
1
2
lim
+
∞→
⎟
⎠
⎞
⎜
⎝
⎛
+
+
n
n
n
n
.
3.7. 1)
5015
25152
lim
2
2
++
++
→
x
x
xx
cx
, если а) с = 5; б) с = – 5; в) с = ∞;
2)
xtg
xtg
x
15
5
lim
0→
; 3)
14
2
32
lim
−
∞→
⎟
⎠
⎞
⎜
⎝
⎛
+
n
n
n
n
.
3.8. 1)
43
65
lim
2
2
−+
−+
→
x
x
xx
cx
, если а) с = 2; б) с = 1; в) с = ∞;
2)
x
x
x
2
0
sin
6cos1
lim
−
→
; 3)
n
n
n
n
21
2
1
lim
+
∞→
⎟
⎠
⎞
⎜
⎝
⎛
+
.
3.9. 1)
54
853
lim
2
2
−+
−+
→
x
x
xx
cx
, если а) с = 4; б) с = 1; в) с = ∞;
2)
xtg
x
x
2
3sin
lim
0→
; 3)
()
x
x
x
3
0
51lim +
→
.
3.10. 1)
43
2
lim
2
2
−−
−−
→
x
x
xx
cx
, если а) с = 0; б) с = – 1; в) с = ∞;
2)
2
0
4cos1
lim
x
x
x
−
→
; 3)
()
x
x
x
4
0
81lim +
→
.
2.3. Понятие неопределенного интеграла
В дифференциальном исчислении решается задача: по данной функции
f (х) найти ее производную (или дифференциал). Интегральное исчисление
решает обратную задачу: найти функцию F (х), зная ее производную
(
)
=
′
xF
14

()
xf=
(или дифференциал). Искомую функцию F (х) называют первообраз-
ной
функции f (х). Действие нахождения первообразной для определенной
функции f (х) называется
интегрированием этой функции. Итак, если F (х)
есть какая-то первообразная для f (х), то выражение
F (х) + с, где с момент
принимать любое постоянное значение, называется
неопределенным инте-
гралом
функции f (х) и обозначается через
(
)
∫
dxxf
. Таким образом, по оп-
ределению
(
)
(
)
cxFdxxf +=
∫
.
Здесь f (х) называется подынтегральной функцией,
(
)
−dxxf
подынтеграль-
ным выражением, х – переменной интегрирования, знаком неопределенно-
го интеграла.
∫
−
Основные свойства неопределенного интеграла
а) производная неопределенного интеграла равна подын-
тегральной функции;
()
()
()
−=
′
∫
xfdxxf
б)
() () ()()
(
)
(
)
(
)
∫∫∫∫
−−+=−+ dxxhdxxgdxxfdxxhxgxf
интеграл от алгеб-
раической суммы нескольких функций равен алгебраической сумме инте-
гралов от этих функций;
в) постоянный множитель можно выносить за знак
интеграла.
() ()
−=
∫∫
dxxfadxxaf
Таблица простейших интегралов
1. ; 2.
∫
+= cxdx
()
1
1
1
−≠α+
+α
+
=
∫
α
α
c
x
dxx
;
3.
∫
+= cx
x
dx
ln
; 4.
()
1,0
ln
≠>+=
∫
aac
a
a
dxa
x
x
;
5. ; 6. ;
∫
+= cedxe
xx
∫
+−= cxdxx cossin
7. ; 8.
∫
+= cxdxx sincos
∫
+−= cxdxtgx cosln
;
9.
∫
+= cxdxctgx sinln
; 10.
∫
+= ctgx
x
dx
2
cos
;
15
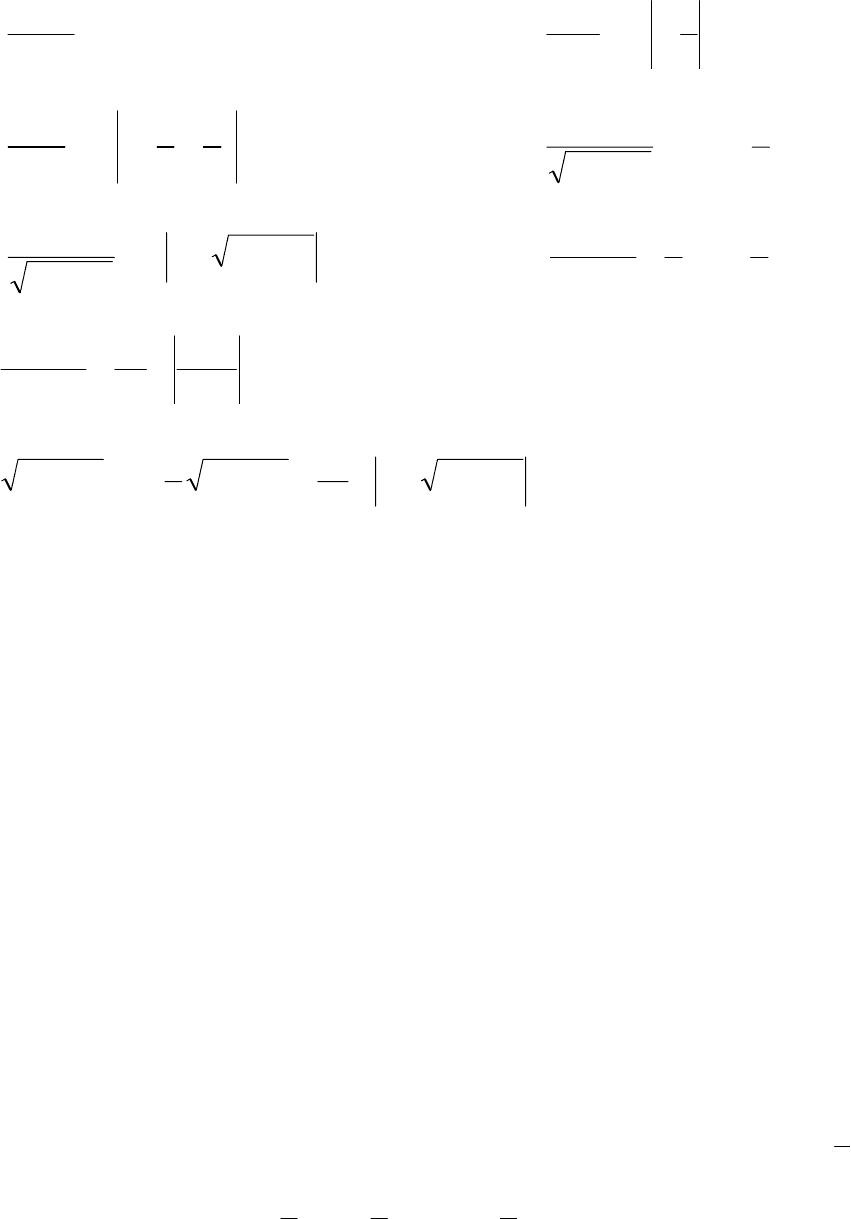
11.
∫
+−= cctgx
x
dx
2
sin
; 12.
∫
+= c
x
tg
x
dx
2
ln
sin
;
13.
∫
+
⎟
⎠
⎞
⎜
⎝
⎛
π
+= c
x
tg
x
dx
42
ln
cos
; 14.
∫
+=
−
c
a
x
xa
dx
arcsin
22
;
15.
∫
+++=
+
caxx
ax
dx
22
22
ln ; 16.
∫
+=
+
c
a
x
arctg
axa
dx 1
22
;
17.
∫
+
−
+
=
−
c
xa
xa
axa
dx
ln
2
1
22
;
18.
∫
+±+±±=± caxx
a
ax
x
dxax
22
2
2222
ln
22
.
Основные методы интегрирования
а) Метод введения нового аргумента. Если
(
)
(
)
cxFdxxf +=
∫
, то
(
)
=
∫
duuf
()
cuF += , где .
()
xu ϕ=
б) Метод разложения. Если
(
)
(
)
(
)
xfxfxf
21
±
=
, то
(
)()
±=
∫∫
dxxfdxxf
1
()
∫
± dxxf
2
.
в) Метод подстановки. Если f (х) непрерывна, то, полагая , где
()
tx ϕ=
(
)
t
ϕ
непрерывна вместе со своей производной
(
)
t
ϕ
′
, получим:
()
=
∫
dxxf
.
()()()
∫
ϕ
′
ϕ= dtttf
г) Метод интегрирования по частям. Если u и v – некоторые дифференцируе-
мые функции от х, то .
∫∫
−= vduuvudv
Пример 2.4. Найти и проверить результат диффе-
ренцированием.
∫
+
dxxe
x
sin
3cos5
Решение. Положим
t
x
=
+
3cos5, тогда d
t
dx
x
=
−
sin5, dtdxx
5
1
sin −=
,
поэтому
ce
5
1
ce
5
1
dt
5
1
dxxe
3x5t3x5
+−=+−=−=
++
∫
coscos
sin .
Для проверки полученного результата убедимся в том, что производная
от полученного выражения равна подынтегральной функции
16

() ()
xexexece
xxxx
sinsin5
5
1
3cos5
5
1
5
1
3cos53cos53cos53cos5 ++++
=−⋅−=
′
+⋅−=
′
⎟
⎠
⎞
⎜
⎝
⎛
+− .
В результате получили подынтегральную функцию, следовательно, интеграл
найден верно.
Пример 2.5. Найти
(
)
∫
− dxex
x2
2
и проверить результат дифференциро-
ванием.
Решение. Используем формулу интегрирования по частям:
∫∫
−= vduuvudv
.
Пусть 2−=
x
u , d dxe
x2
= . Тогда dxdu
=
,
xx
edxev
22
2
1
==
∫
. Поэтому
v
() () ()
ceexdxeexdxex
xxxxx
+−−=−−=−
∫∫
22222
4
1
2
2
1
2
1
2
2
1
2
.
Для проверки полученного результата возьмем производную от правой
части полученного выше выражения:
() () ()
xxxxxx
exeexeceex
222222
22
4
1
2
2
1
2
1
4
1
2
2
1
−=⋅⋅−+=
′
⎟
⎠
⎞
⎜
⎝
⎛
+−−
, что под-
тверждает правильность полученного результата.
Пример 2.6. Найти
∫
++
+
dx
xx
x
328
54
2
и проверить результат дифферен-
цированием.
Решение. Преобразуем подынтегральную функцию и используем заме-
ну переменной:
()
()
()
()
()
()
.
4
4
4
11
328ln2
4
4
4
11
164ln2
44
11
16ln2
4
11
16
2
2
16
11
16
4
16
114
16
544
4
4
164
54
328
54
2
2
2
22222
22
2
2
c
x
arctgxxc
x
arctgx
c
t
arctgt
t
dt
t
t
t
dt
dt
t
t
dt
t
t
dt
t
t
dtdx
tx
tx
dx
x
x
dx
xx
x
+
+
−++=+
+
−++=
=+−+=
+
−
+
=
+
−
+
=
=
+
−
=
+
+−
=
=
−=
=
+
=
++
+
=
++
+
∫∫∫∫
∫∫∫∫
Проверим ответ дифференцированием:
17
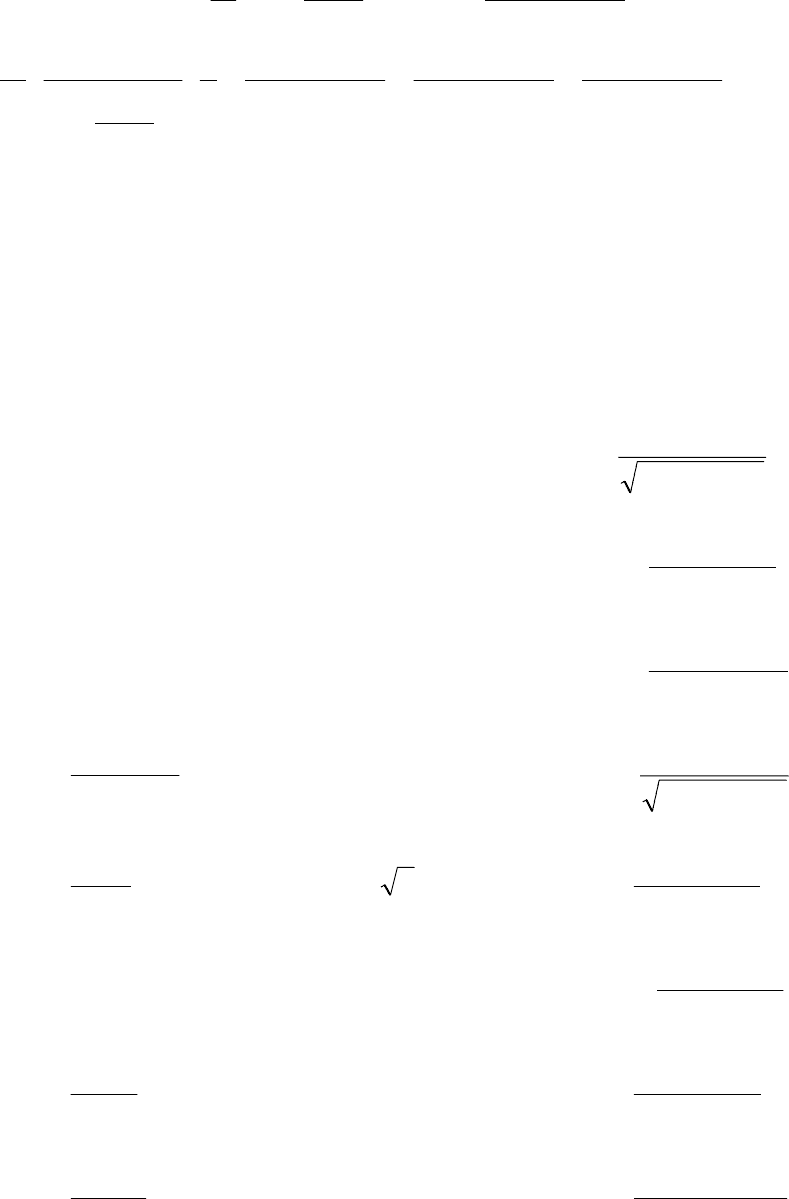
()
()
.
328
54
328
11
328
164
4
1
4
4
1
1
4
11
82
328
1
2
4
4
4
11
328ln2
222
2
2
2
++
+
=
++
−
++
+
=⋅
⎟
⎠
⎞
⎜
⎝
⎛
+
+
⋅−
−+⋅
++
⋅=
′
⎟
⎠
⎞
⎜
⎝
⎛
+
+
−++
xx
x
xxxx
x
x
x
xx
c
x
arctgxx
В результате получим подынтегральную функцию, следовательно, ин-
теграл найден верно.
2.4. Задача 4 для контрольной работы
Найти неопределенные интегралы. Результаты проверить дифференци-
рованием.
4.1. а) ; б) ; в)
()
∫
+
+
dxxe
xx
1
2
2
∫
dxxx 3sin
∫
++ 54
2
xx
dx
.
4.2. а) ; б) ; в)
()
∫
+ dxxx
6
2
53
∫
dxxx ln
5
dx
xx
x
∫
++
+
52
32
2
.
4.3. а) ; б) ; в)
∫
+
dxxe
x
cos
5sin3
∫
dxxe
x5
dx
xx
x
∫
++
+
106
14
2
.
4.4. а)
∫
+ 8sin3
cos
x
dxx
; б) ; в)
∫
dxxx 4cos
dx
xx
x
∫
−−
+
2
22
52
.
4.5. а)
∫
xx
dx
ln
; б)
∫
dxxx ln ; в) dx
xx
x
∫
++
+
84
3
2
.
4.6. а) ; б) ; в)
()
∫
+
+
dxx2x3
4
10
25
∫
dxxx 4sin
dx
xx
x
∫
+−
+
52
13
2
.
4.7. а)
∫
+
4
1 x
dxx
; б) ; в)
∫
dxxx ln
4
∫
++ 65
2
xx
dx
.
4.8. а) dx
x
arctgx
∫
+
2
1
; б) ; в)
∫
dxxx 5sin
∫
++ 2610
2
xx
dxx
.
18

4.9. а) ; б) ; в)
∫
dxxtg3
∫
dxxx 6cos
dx
xx
x
∫
+−
+
54
1
2
.
4.10. а)
∫
−13
4
3
x
dxx
; б) ; в)
∫
dxxe
x5
dx
xx
x
∫
+−
−
208
14
2
.
2.5. Определенный интеграл. Основные понятия
Пусть функция f (х) определена на отрезке
[
]
ba,
. Разделим этот отрезок
на n произвольных частей. Обозначим абсциссы точек деления через
bxxxxxxxa
n1ii3210
=
<
<
<
<
<
<
<
<=
+
……
.
В каждом частичном промежутке возьмем произвольную точку . Умножив
значение функции на длину соответствующего промежутка, получим
i
ξ
(
i
f ξ
)
()( )
(
)
(
)
11 ++
≤
ξ
≤
Δ
ξ
=
−
ξ
iiiiiiii
xxxfxxf
.
Составим сумму которую называют
интегральной суммой
функции f (х) отрезка
[
и перейдем к пределу
()
∑
−
=
Δξ=σ
1n
oi
ii
xf
]
ba,
, (2.1)
()
∑
−
=
→λ
Δξ
1
0
lim
n
oi
ii
xf
где наибольшая из разностей −λ
iii
xxx
−
=
Δ
+1
.
Если существует конечный предел (2.1), не зависящий ни от способа
дробления, ни от выбора точек
i
ξ
в соответствующих частичных промежут-
ках , то он называется
определенным интегралом функции f (х) в проме-
жутке от а до b и обозначается символом , где а и b называют верх-
ним и нижним пределами интегрирования соответственно, – подын-
тегральным выражением и х – переменной интегрирования.
i
xΔ
()
∫
b
a
dxxf
()
∫
b
a
dxxf
Простейшие свойства определенного интеграла
1. ;
() () ()
∫∫∫
==
b
a
b
a
b
a
dzzfdttfdxxf
2.
;
()
0=
∫
a
a
dxxf
19

3.
;
() ()
∫∫
−=
a
b
b
a
dxxfdxxf
4.
;
() () ()
∫∫∫
+=
b
c
c
a
b
a
dxxfdxxfdxxf
5.
;
() ()
∫∫
=
b
a
b
a
dxxfkdxxkf
6. .
() () ()( ) () () ()
∫∫∫∫
−+=−+
b
a
b
a
b
a
b
a
dxxhdxxqdxxfdxxhxqxf
Вычисление определенных интегралов с помощью неопределенных
Формула Ньютона-Лейбница. Если функция f (х) определена и непре-
рывна на отрезке и F (х) – ее первообразная, т.е.
[
ba,
]
(
)(
xfxF =
)
′
, то
() () () ()
a
b
xFaFbFdxxf
b
a
=−=
∫
.
Формула интегрирования по частям. Если f (х) и g (х) гладкие на
[
]
ba,
,
то
() () ()() () ()
∫∫
′
−=
′
b
a
b
a
dxxfxg
a
b
xgxfdxxgxf
.
Замена переменной. Если: 1) функция f (х) непрерывна на
[
]
ba,
; 2)
функция непрерывна вместе со своей производной
()
tϕ
()
t
ϕ
′
на отрезке
[
]
β
α
,
,
где , ; 3) сложная функция
()
αϕ=a
()
βϕ=b
(
)
(
)
t f
ϕ
определена и непрерывна
на
[
, то
]
βα,
() ()()()
∫∫
β
α
ϕ
′
ϕ= dttxfdxxf
b
a
.
Геометрические приложения определенного интеграла
1.
Вычисление площадей.
Площадь фигуры
1221
BBAAS
=
(рис. 1.2.), ограниченной двумя непре-
рывными кривыми и
()
xyy
1
=
(
)
xyy
2
=
(
)
(
)
(
)
xyxy
12
≥
и двумя прямыми х = а
и х = b (а < b) равна
20
