ДеМерс Майкл Н. Географические информационные системы. Основы

Подождите немного. Документ загружается.

единицу на каждую проходимую ячейку растра. Подойдя же к барьеру, мы

должны приложить в пять раз больше усилий (выражаемых количеством

бензина, времени, или потерей скорости движения) на преодоление только

одной ячейки, принадлежащей барьеру, чтобы попасть за него. То есть, если

до барьера график затрат выглядел бы как наклонная прямая линия, то в

месте барьера на этом графике появится вертикальный скачок. Такой барьер

называется относительным (или условным), так как он может быть

преодолен при приложении дополнительных усилий.

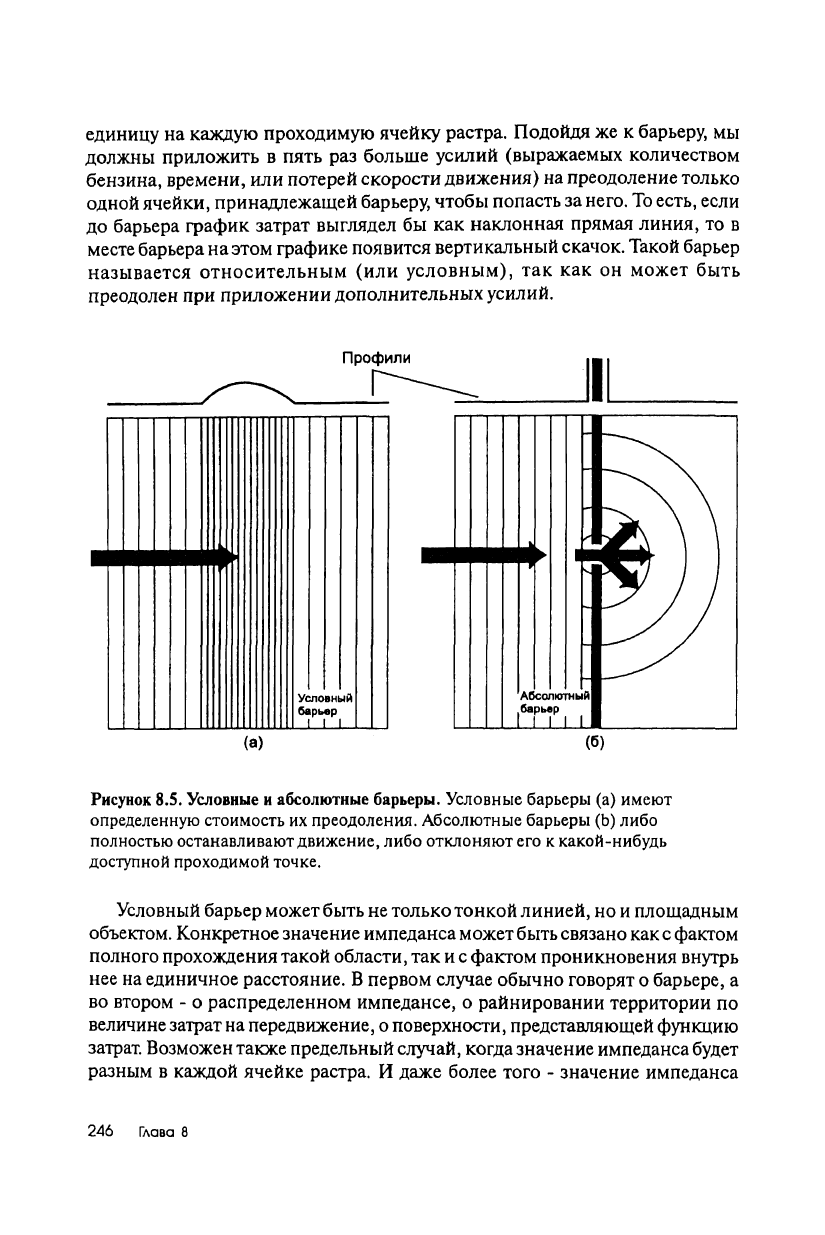
Рисунок 8.5. Условные и абсолютные барьеры. Условные барьеры (а) имеют

определенную стоимость их преодоления. Абсолютные барьеры (Ь) либо

полностью останавливают движение, либо отклоняют его к какой-нибудь

доступной проходимой точке.

Условный барьер может быть не только тонкой линией, но и площадным

объектом. Конкретное значение импеданса может быть связано как с фактом

полного прохождения такой области, так и с фактом проникновения внутрь

нее на единичное расстояние. В первом случае обычно говорят о барьере, а

во втором - о распределенном импедансе, о райнировании территории по

величине затрат на передвижение, о поверхности, представляющей функцию

затрат. Возможен также предельный случай, когда значение импеданса будет

разным в каждой ячейке растра. И даже более того - значение импеданса

даже в одной ячейке может быть различным при передвижении через нее по

разным направлениям. Например, оно может зависеть от направления ветра

или от ориентации снежных застругов в тундре.

Абсолютный барьер можно представить себе как некоторое продолжение

идеи условного барьера. Для линейного объекта мы просто присвоить ему

значение импеданса, непреодолимое в рамках решаемой задачи. На Рисунке

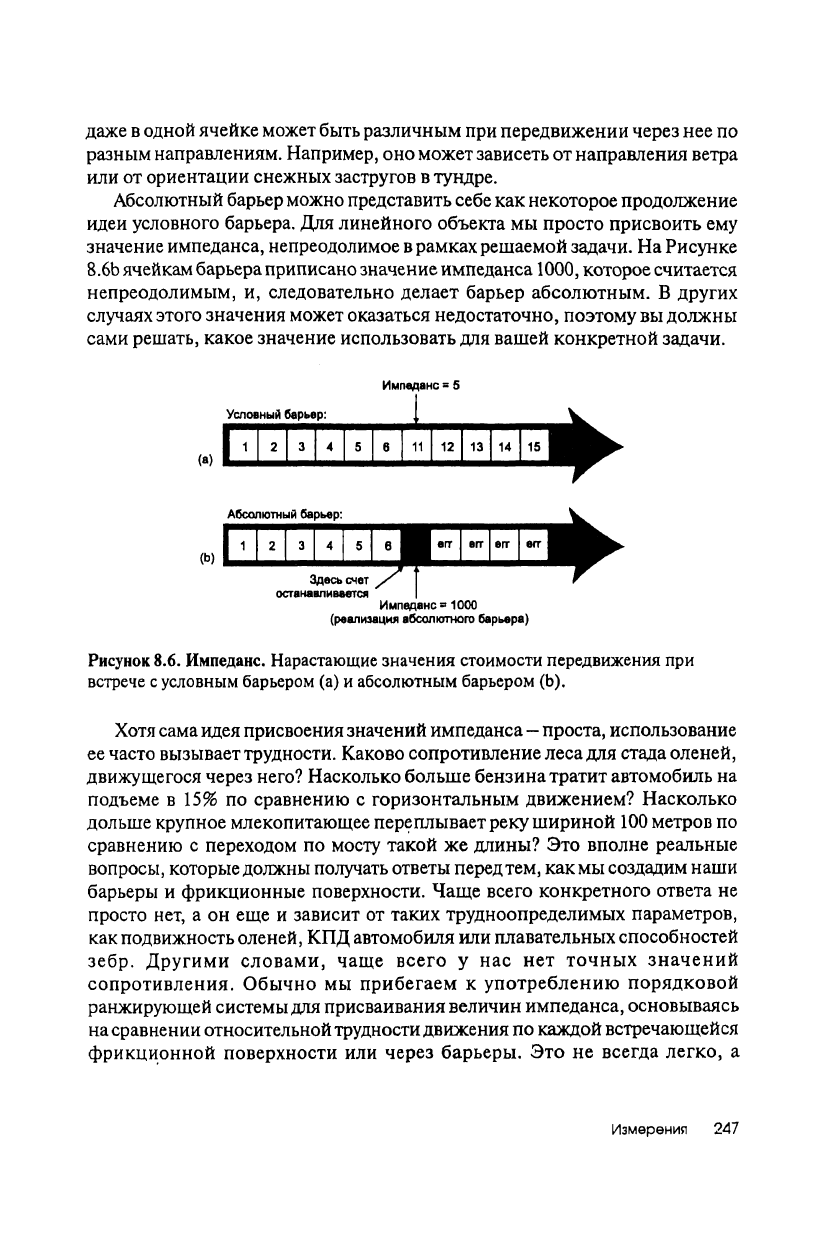
8.6Ь ячейкам барьера приписано значение импеданса 1000, которое считается

непреодолимым, и, следовательно делает барьер абсолютным. В других

случаях этого значения может оказаться недостаточно, поэтому вы должны

сами решать, какое значение использовать для вашей конкретной задачи.

Импеданс

= 5

Условный

барьер:

(а)

12 13

Абсолютный

барьер:

(Ь)

6 err err err err ^^^^^^

Здесь счет

останавливается

Импеданс»

1000

(реализация абсолютного

барьера)

Рисунок 8.6. Импеданс. Нарастающие значения стоимости передвижения при

встрече

условным барьером (а) и абсолютным барьером (Ь),

Хотя сама идея присвоения значений импеданса - проста, использование

ее часто вызывает трудности. Каково сопротивление леса для стада оленей,

движущегося через него? Насколько больше бензина тратит автомобиль на

подъеме в 15% по сравнению с горизонтальным движением? Насколько

дольше крупное млекопитающее переплывает реку шириной 100 метров по

сравнению с переходом по мосту такой же длины? Это вполне реальные

вопросы, которые должны получать ответы перед тем, как мы создадим наши

барьеры и фрикционные поверхности. Чаще всего конкретного ответа не

просто нет, а он еще и зависит от таких трудноопределимых параметров,

как подвижность оленей, КПД автомобиля или плавательных способностей

зебр.

Другими словами, чаще всего у нас нет точных значений

сопротивления. Обычно мы прибегаем к употреблению порядковой

ранжирующей системы для присваивания величин импеданса, основываясь

на сравнении относительной трудности движения по каждой встречающейся

фрикционной поверхности или через барьеры. Это не всегда легко, а

результаты

не так

точны,

как нам

хотелось

бы. В

установке этих величин

рекомендуется действовать

осторожностью, убедившись,

что

использованная система достаточно обоснована,

и что

сравнения

допустимы. Прежде всего, результаты анализа расстояний

использованием

барьеров

фрикционных поверхностей должны рассматриваться

определенной критичностью, особенно если

эти

результаты используются

для принятия каких-либо решений.

Перед тем,

как

приступить

растровым подходам

для

неэвклидовых

функциональных расстояний, мы должны рассмотреть две дополнительные

характеристики расстояний. Расстояние может рассматриваться

не

только

как эвклидово или неэвклидово, изотропное или функциональное, но также

как

инкрементное, или нарастающее расстояние

(incremental or cumulative

distance).

Инкрементное расстояние складывается

из

длин этапов

пройденного пути. Каждый последующий этап добавляется просто как мера

длины, наподобие того,

как это

делалось

изотропной поверхностью.

Другими словами, инкрементное расстояние

- это

кратчайший путь между

двумя точками

без

учета сопротивления

пути. Если инкрементное

расстояние измеряется

по

всей поверхности,

то в

результате

мы

получаем

поверхность кратчайших расстояний

(shortest path surface),

если же этот метод

ограничивается линиями

или

дугами

(или

линейными группами ячеек

растра),

то мы

имеем дело

линиями кратчайших расстояний,

а не с

поверхностью.

Целью определения функционального расстояния

на

поверхности

сопротивлением (например, топографической) является поиск маршрута

наименьшей стоимости

(least-cost distance), или

кратчайшего расстояния

между двумя точками покрытия*. Аналогично

мы

можем построить

поверхность наименьшей стоимости

для

перемещения

из

одной точки

во

все другие точки покрытия. Рассмотрим два этих случая

по

отдельности.

Допустим, что мы имеем дело с реальной топографической поверхностью,

и стоимость связана с изменением значения высоты от ячейки

ячейке.

Мы

могли

бы

поместить каплю воды

на

вершину нашей поверхности

проследить ее движение, которое будет путем наименьшего сопротивления.

Между прочим, многие программы используют

качестве команд такие

слова как

"drain"

(сток)

или "stream"

(поток, река). Для создания маршрута

наименьшей стоимости

(в

противоположность кратчайшему маршруту)

на

растре размером

5x5 мы

начинаем

верхней ячейки

ищем среди восьми

соседей ячейку

наименьшим значением импеданса

(в

данном случае

—

наименьшим значением высоты).

Эта

ячейка помечается флажком

становится начальной точкой

для

следующей итерации. Процесс

* В реальных задачах обычно учитываются стоимостные показатели нескольких покрытий,

которые

помощью весовой функции сводятся

некоторому общему стоимостному покрытию.

О построении таких поверхностей

см.

пример

Главе

13.

— прим. перев.

продолжается, пока

не

будет достигнута наименьшая высота покрытия.

Таким образом,

из

отмеченных ячеек

мы

получаем маршрут

от

вершины

холма

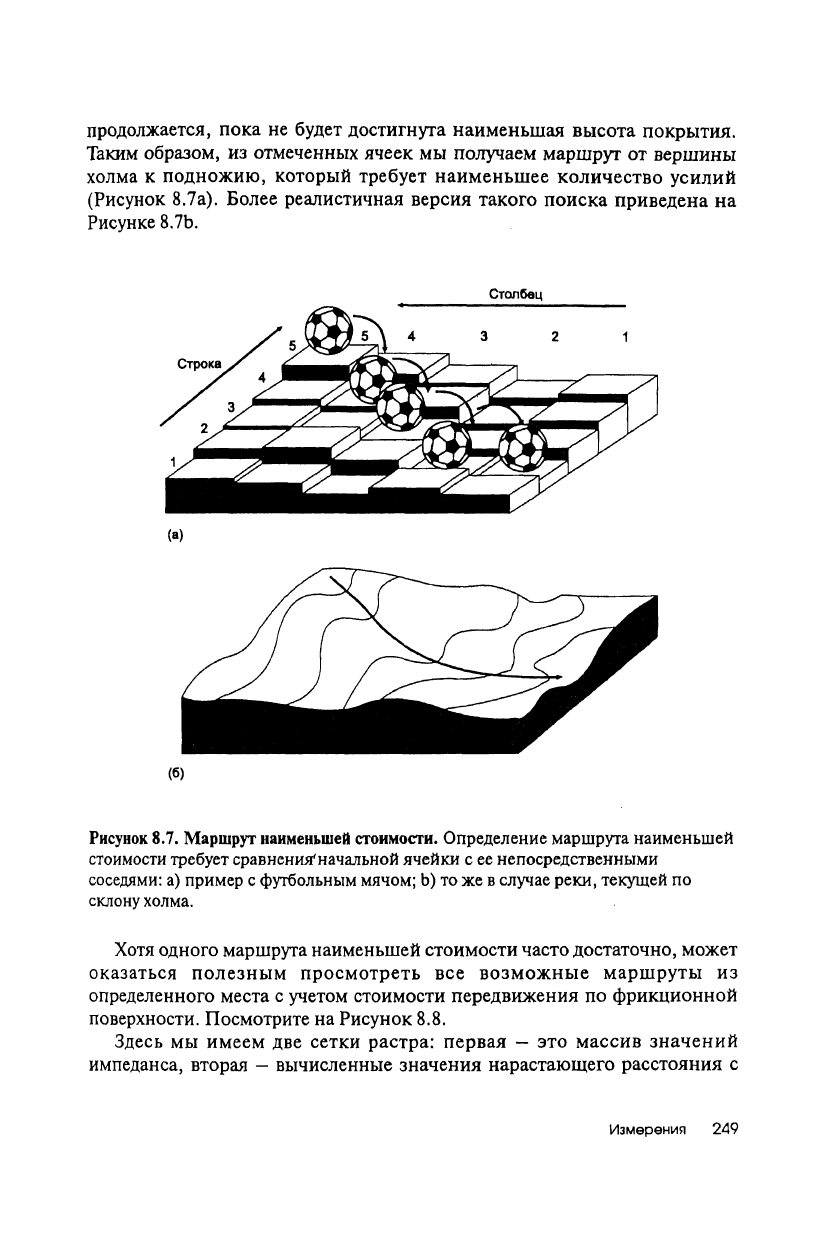
подножию, который требует наименьшее количество усилий

(Рисунок 8.7а). Более реалистичная версия такого поиска приведена

на

Рисунке 8,7Ь.

Столбец

(б)

Рисунок

8.7.

Маршрут наименьшей стоимости.

Определение маршрута наименьшей

стоимости требует сравнения'начальной ячейки

ее непосредственными

соседями:

а)

пример

футбольным мячом; Ь) то же в случае реки, текущей

по

склону холма.

Хотя одного маршрута наименьшей стоимости часто достаточно, может

оказаться полезным просмотреть

все

возможные маршруты

из

определенного места

учетом стоимости передвижения

по

фрикционной

поверхности. Посмотрите

на

Рисунок

8.8.

Здесь

мы

имеем

две

сетки растра: первая —

это

массив значений

импеданса, вторая

—

вычисленные значения нарастающего расстояния

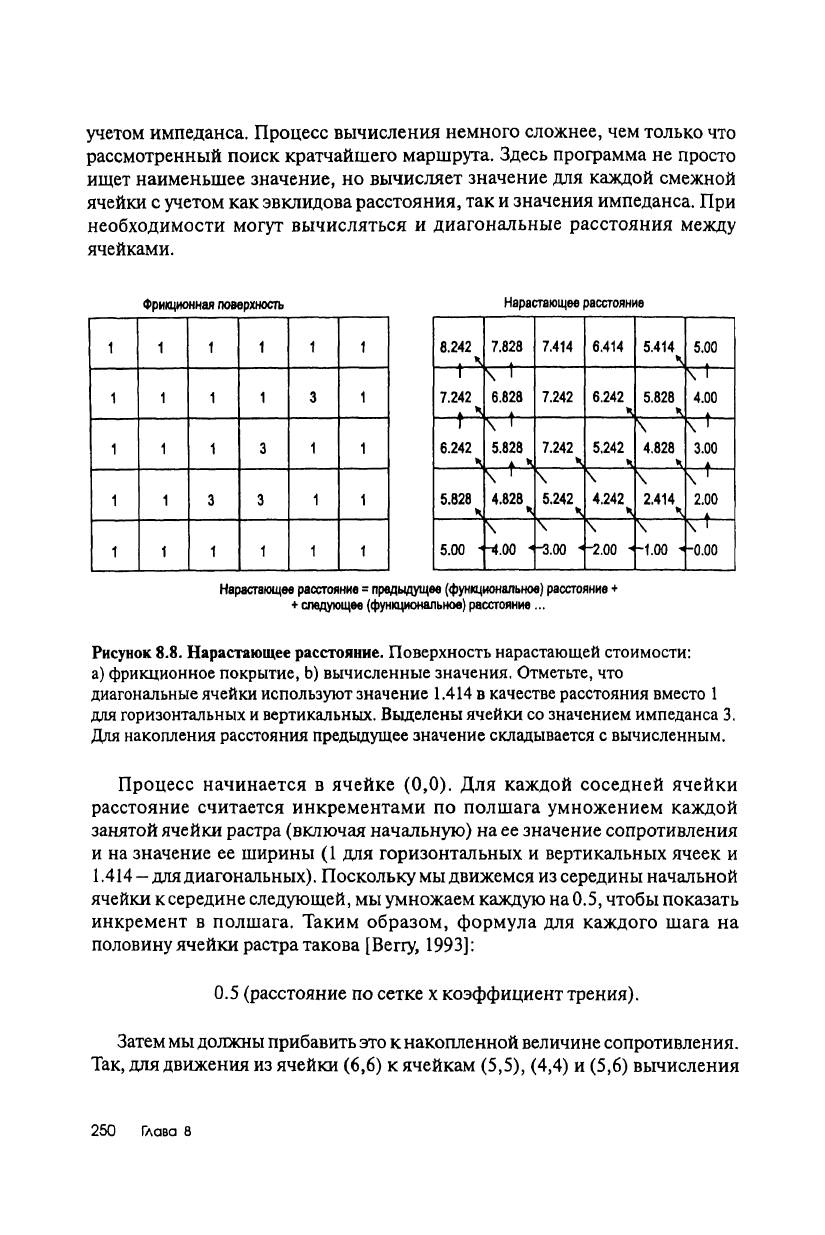
учетом импеданса. Процесс вычисления немного сложнее, чем только что

рассмотренный поиск кратчайшего маршрута. Здесь программа не просто

ищет наименьшее значение, но вычисляет значение для каждой смежной

ячейки с учетом как эвклидова расстояния, так и значения импеданса. При

необходимости могут вычисляться и диагональные расстояния между

ячейками.

Фрикционная поверхность

Нарастающее

расстояние

1 1

8.242

7.828

7.414 6.414

5.414

5.00

7.242

4 Ч

6.828

7.242

6.242

5.828

4.00

6.242

\ т

5.828

7.242

5.242

4.828

3.00

5.828

4.828

5.242

4.242

2.414

2.00

5.00 *

-4.00 «

-з.оо <

-2.00 «

-1.00 -

ч t

-0.00

Нарастающее

расстояние

предыдущее (функциональное) расстояние ^

+ следующее (функциональное) расстояние...

Рисунок

8.8.

Нарастающее расстояние.

Поверхность нарастающей стоимости:

а) фрикционное покрытие, Ь) вычисленные значения. Отметьте, что

диагональные ячейки используют значение 1.414 в качестве расстояния вместо 1

для горизонтальных и вертикальных. Выделены ячейки со значением импеданса 3.

Для накопления расстояния предыдущее значение складывается с вычисленным.

Процесс начинается в ячейке

(0,0).

Для каждой соседней ячейки

расстояние считается инкрементами по полшага умножением каждой

занятой ячейки растра (включая начальную) на ее значение сопротивления

и на значение ее ширины (1 для горизонтальных и вертикальных ячеек и

1.414 - для диагональных). Поскольку мы движемся из середины начальной

ячейки к середине следующей, мы умножаем каждую на 0.5, чтобы показать

инкремент в полшага. Таким образом, формула для каждого шага на

половину ячейки растра такова [Berry,

1993]:

0.5 (расстояние по сетке х коэффициент трения).

Затем мы должны прибавить это к накопленной величине сопротивления.

Так, для движения из ячейки (6,6) к ячейкам

(5,5),

(4,4) и (5,6) вычисления

0.5(1.414x

1.00) = 0.707

0.5(1.414x

1,00) = 0.707

Вместе

= 1.414

Предыдущее

= 0

значение

Итого

= 1.414

0.5(1.414x

1.00) = 0.707

0.5(1.414x3.00)

= 2.121

Вместе

= 2.828

Предыдущее

= 1.414

значение

Итого

= 4.242

0.5(1.000x

1.00) = 0.500

0.5(1.000x

1.00) = 0.500

Вместе

= 1.000

Предыдущее

= 0

значение

Итого

= 1.000

шаг -

выбор наименьшего накопленного расстояния

для

каждой прилежащей ячейки. Затем процесс повторяется. Расстояния

сопротивлением

на

всех шагах складываются вместе

для

получения

нарастающего итога. Как видите, процесс довольно утомителен,

вот почему

мы используем компьютеры.

результате

мы

получаем поверхность

наименьшей стоимости,

а не

один маршрут,

и мы

можем выбрать маршрут

наименьшей стоимости

из

любой

и в

любую точку покрытия. Это делается

просто выбором смежных ячеек

наименьшими значениями стоимости.

В случае векторных координат, описывающих точечные, линейные

площадные объекты,

для

определения расстояний может использоваться

серия модификаций стандартной теоремы Пифагора. Вначале вспомним

исходную формулу для эвклидова или прямолинейного расстояния между

двумя точками.

Однако, если

мы не

можем двигаться

по

прямой, т.е. имеется некоторое

препятствие, вынуждающее

нас

отклоняться

от

прямой,

то мы

можем

обобщить эту формулу

неэвклидову форму:

таковы:

5,5

4,4

где степень 2 заменяется на к (соответственно корень будет не второй, а к-й

степени), - некоторое из диапазона возможных значений

[McGrew

and

Monroe,

1993].

Нетрудно заметить, что подстановка к = 2 превращает эту формулу в

предшествующую формулу для расстояния по прямой.

ЕВКЛИДОВО

расстояние

ВДГ

" d=J(X

-X/

-Y/

Манхэттенское расстояние

d=|X

X,|+

|У,-Г

и-

d= \(х

х/

>0.6 , 1/0,6

Рисунок 8.9. Измерение расстояния

векторной модели данных.

Два способа

определения неэвклидова

расстояния,

каждый является модификацией формулы

теоремы

Пифагора,

причем

формуле

меняется

только параметр

к.

Допустим, например, что мы ищем расстояние между двумя точками в

Манхэттене, где десятки высоких зданий и кварталы ограничивают наше

движение отрезками под прямым углом друг к другу. В этом случае мы имеем

значительные ограничения движения, и переменная к принимает значение

а формула расстояния принимает вид:

Как видите, любое расстояние в векторной БД может быть определено

простым изменением параметра к в соответствии с имеющимися условиями

(Рисунок 8.9). Значение к = 1.5 соответствует случаю где-то между

манхэттенским и эвклидовым расстоянием. Даже фрикционные

поверхности могут оцениваться с помощью этой формулы. Например, к =

0.6 позволяет нам найти кратчайшее расстояние вокруг некоторого барьера,

такого как озеро.

Мы можем определять кратчайшие маршруты и маршруты наименьшей

стоимости с учетом импеданса и барьеров также и в случае движения по

сетям. Однако, этот вопрос относится скорее к связности, чем к измерению

расстояний, так что мы рассмотрим его в Птве 11.

Вопросы

Опишите простейший из возможных методов измерения линии в

растре. Как полученный таким образом результат может быть преобразован

в реальную меру длины при горизонтальном или вертикальном

расположении ячеек растра? Что делать, если они расположены

диагонально?

2. Каковы возможные проблемы при измерении длины в растре,

особенно с учетом того, какячейки растра представляют линейные объекты?

3. Как измерить длину извилистого линейного объекта в векторной

системе? Как соотносятся длина оцифрованной линии в векторной системе

с длиной этой линии при ее измерении на местности?

4. Для чего измеряются большая и малая оси полигона?

5. Почему важно отношение между периметром и площадью полигона?

Как различия в этом отношении могут быть значимы в естественной среде?

Как - в антропогенной?

6. Как измеряется периметр полигона в векторной модели? Как - в

растровой?

7. Как измеряется площадь полигона в векторной модели? Как - в

растровой?

8. Зная о связи между формой объектов и их функцией, почему в ГИС

имеется так мало рабочих методов анализа формы?

9. Опишите два метода измерения извилистости линейных объектов.

Приведите два примера таких мер, которые могли бы быть полезны для

пользователя ГИС.

10. Что такое пространственная целостность? Как мы можем ее измерить?

Почему число Эйлера не определяется однозначно количеством отверстий

и числом областей региона?

11.

Опишите, как может быть измерена конфигурация границы полигона.

Что такое мера выпуклости? Почему крут наиболее часто используется для

сравнения с ним полигональных фигур?

12. Как может использоваться скользящее окно для определения меры

конфигурации границы полигона в растре?

13. Как измеряется расстояние от некоторой точки ко всем другим точкам

покрытия в растре? Что такое изотропная поверхность, и каково ее значение?

14. Что такое фрикционная поверхность? Барьер? Каковы два типа

барьеров? Какая связь существует между условным барьером и фрикционной

поверхностью?

15. Опишите простой растровый метод измерения расстояния на

фрикционной поверхности.

16. Какова разница между инкрементным и нарастающим расстоянием?

Как мы можем определить путь наименьшего сопротивления (наилучший

путь) по растровому покрытию? Каков более точный метод измерения

нарастающего расстояния (поверхности наилучшего пути) в растровой ГИС

по сравнению с простым сложением значений сопротивления?

17. Как мы можем модифицировать теорему Пифагора для учета

движения вдоль городских кварталов, вокруг барьеров и по фрикционным

поверхностям в векторной системе?

18. Каковы потенциальные проблемы выбора значений импеданса для

моделирования расстояния?

Глава

Классификация

Классификация наземных объектов

—

старая проблема.

Она

привлекала

умы ученых разных направлений, каждый

из

которых смотрел

на

Землю

своими глазами, используя свой лексикон

свой интеллектуальный фильтр.

Хотя идея классификации разбросанных

по

поверхности Земли объектов

кажется довольно простой, практические аспекты этой задачи далеки

от

полной очевидности.

То, как мы

классифицируем

то, что

видим, получит

отображение

в том, как мы

анализируем данные,

и что

означают наши

выводы.

На

самом деле,

то, как мы

классифицируем данные, может даже

предопределять, какие выводы

мы

получим.

этому процессу нельзя

относиться беспечно, так как плохая классификация может сбить нас

пути.

Давайте посмотрим назад,

начало 19-го века, когда путешественники,

двигавшиеся

по

местам,

где

теперь находятся центральные штаты

США,

классифицировали луга центральных равнин. Термин, который

они

использовали,

был

"Великая американская пустыня". Слово "пустыня"

предполагает,

что эти

области

не

пригодны

для

земледелия.

Однако

мы

знаем,

что в

действительности

это

была прерия (степь),

а не

пустыня,

и ее

производство зерна снискало

ей

звание "мировой хлебной

корзины".

Вот

—

два

совершенно разных взгляда.

Более современный пример также показывает,

как

неправильная

классификация может сбить с толку тех, кто принимает решения. Допустим,

в нашем распоряжении есть ГИС, созданная первопроходцем

этой области.

Среди многих тематических покрытий имеется одно

под

названием

"тип

ландшафта",

котором присутствует категория

под

названием "мокрые

земли" (болота)

(wetlands).

Вроде,

нет

проблем

мокрые,

так

мокрые*.

Но

перед тем как двигаться дальше, давайте рассмотрим следующие вопросы

утверждения. Допустим,

у вас

есть большой приусадебный участок,

полгектара

(5000

кв.м). Вы только

что его

полили,

теперь

на нем

имеются

участки стоячей воды.

Это

мокрые земли?

Или

мокрые земли

это

противоположность плоскогорья

(uplands)?

Некоторые признанные системы

русском языке

нет

эквивалента слову

wetlands,

обычный перевод "болото"

или

"топь"

(которым больше соответствуют

swamp и marsh)

—

весьма приблизителен.

Но

даже

тех,

для

кого английский язык

родной, есть сложности

точным определением этого термина,

что

показывает приводимый автором пример.

—

прим. перев.