Deitz J.E., Southam J.L. Contemporary Business Mathematics for Colleges
Подождите немного. Документ загружается.


36. 37. 38. 39.
40. 5 41. 5 42. 43. 5
55 5
Score for D (24)
2 1
5
6
52 2
2
3
52 1
3
4
52 2
5
6
5
4
2
5
56
7
8
5 3
3
5
53
2
3
5
2 1
1
12
52
5
16
52 1
5
12
2
3
8
2
3
4
5
3
4
5 2
7
12
5
8
D (24 points) Subtract the following fractions and mixed numbers.Write the answers as proper fractions
or mixed numbers, with fractions in lowest terms. (3 points for each correct answer)
44 Part 1 Fundamental Review
Assignment 2.1 Continued
E (25 points) Business Applications and Critical Thinking. Solve the following.Write your answers as
fractions or mixed numbers in lowest terms. (5 points for each correct answer)
44. A restaurant sells three different hamburgers, based on the amount of meat used: “The Mini” ; “The
Regular” ; and “The Maxi” . Students bought one of each to compare them. What was the total
amount of meat used in the three hamburgers?
45. Jared Sines specializes in custom faux painting, but for the first coat he could combine leftover paints
when the colors were relatively the same. He has three containers of different shades of white: quarts,
quarts, and quarts. If Jared combines the contents of all the containers, how many quarts of paint
will he have?
46. Contractor Don Fleming has a top board that is inch thick. Don wants to use wood screws to attach it
to a bottom board. If a wood screw is inches long, how much of the screw will be left over to go into
the bottom board?
47. Robert Landles is planning to attach a plywood panel to a wall using nails that are inches long. The panel
is inch thick. Beneath the panel is a layer of sheetrock that is inch thick. How many inches of the nail
should go into the wood frame that is underneath the sheetrock?
48. Paris Fabric Center sold four pieces of wool fabric to a tailor. The pieces measured yards, yards,
yards, and yards in length. How many yards of fabric did the tailor purchase?
Score for E (25)
4
1
2
1
3
4
2
1
3
3
1
4
1
2
3
8
1
3
4
1
1
2
13
16
2
1
2
2
3
4
2
2
3
(
1
2
lb)(
1
3
lb)
(
1
5
lb)
1
8
12
5 1
2
3
7
16
1
2
12
5 1
1
6
2
8
5
1
4
2
17
30
4
5
24
1
17
20
5
6
2
5
16
12
16
2 1
1
12
2
9
12
2 2
5
6
2 2
5
6
2
10
6
3
4
6
21
15
20
21
15
20
2
32
20
3
12
20
21
25
30
21
25
30
3
42
30
4
12
30
2 2
16
24
6
21
24
2
2
3
1 2
3
4
1 2
1
2
5 2
8
12
1 2
9
12
1 2
6
12
5 6
23
12
5 7
11
12
qt
1
1
2
2
13
16
5 1
8
16
2
13
16
5
24
16
2
13
16
5
11
16
in.
yd purchased3
1
4
1 2
1
3
1 1
3
4
1 4
1
2
5 3
3
12
1 2
4
12
1 1
9
12
1 4
6
12
5 10
22
12
5 11
10
12
5 11
5
6
(plywood plus sheetrock) to go into wood frame1
3
4
7
8
1
6
8
7
8
14
8
7
8
7
8
in.
3
8
1
1
2
5
3
8
1
4
8
5
7
8
in.
7
11
12
qt
11
16
in.
7
8
in.
11
5
6
yd
1
5
1
1
3
1
1
2
5
6
30
1
10
30
1
15
30
5
31
30
5 1
1
30
lb
1
1
30
lb

Chapter 2 Fractions 45
Assignment 2.2: Multiplication and Division of Fractions
Name
Date Score
A (32 points) Change whole or mixed numbers to improper fractions and multiply. Cancel if possible.
Where the word of appears, replace it with the multiplication symbol.Write the answers as mixed num-
bers or proper fractions in lowest terms. (4 points for each correct answer)
1. 2.
3. 4.
5. 6.
7. 8.
Score for A (32)
B (32 points) Change the mixed numbers to improper fractions and divide. Cancel where possible.Write
the quotients as mixed numbers or proper fractions in lowest terms. (4 points for each correct answer)
9. 10.
11. 12.
13. 14.
3
5
6
4 1
7
12
56
1
4
4 4
3
8
5
7
10
4 2
4
5
5
5
6
4
4
9
4
15
4
7
10
5
7
8
4
3
4
5
1
1
3
3 1
7
8
3 1
1
5
51
7
8
3 12 3
3
10
5
3
8
of 12 54
1
2
3 1
5
9
5
5
18
3
4
9
3
3
10
5
3
4
of
5
6
5
3
10
3
6
7
3
5
6
5
4
15
3
5
8
5
1
Learning Objectives
2 5 6
3
10
3
6
7
3
5
6
5
3 3 1 3 1
2 3 7 3 1
5
3
14
4
15
3
5
8
5
1 3 1
3 3 2
5
1
6
5
18
3
4
9
3
3
10
5
1 3 1 3 1
9 3 3 3 1
5
1
27
3
4
3
5
6
5
1 3 5
4 3 2
5
5
8
3
8
3
12
1
5
3 3 3
2 3 1
5
9
2
5 4
1
2
9
2
3
14
9
5
1 3 7
1 3 1
5
7
1
5 7
4
3
3
15
8
3
6
5
5
1 3 1 3 3
1 3 1 3 1
5 3
15
8
3
12
1
3
3
10
5
3 3 3 3 3
2 3 1 3 2
5
27
4
5 6
3
4
4
15
4
7
10
5
4
15
3
10
7
5
4 3 2
3 3 7
5
8
21
7
8
4
3
4
5
7
8
3
4
3
5
7 3 1
2 3 3
5
7
6
5 1
1
6
7
10
4
14
5
5
7
10
3
5
14
5
1 3 1
2 3 2
5
1
4
5
6
4
4
9
5
5
6
3
9
4
5
5 3 3
2 3 4
5
15
8
5 1
7
8
23
6
4
19
12
5
23
6
3
12
19
5
23 3 2
1 3 19
5
46
19
5 2
8
19
25
4
35
8
25
4
8
35
5 2
1 7
10
7
1
3
7
1
6
3
14
5
8
1
27
7
6
3
4
1
1
6
8
21
2
8
19
1
4
1
3
7
5 1
7
8
3
4
1
2

15. 16.
Score for B (32)
C (36 points) Business Applications and Critical Thinking. Use fractions and mixed numbers to solve each
of the following. State the answers as whole numbers, proper fractions, or mixed numbers in lowest
terms. (6 points for each correct answer)
17. Last week, East Shore Concrete Co. built a small driveway that required cubic yards of concrete.
This week, the company must build another driveway that is times larger. How many yards of
concrete will be required?
18. Athena Nguyen bought eight pieces of copper tubing that were each inches long. What was the total
length of tubing that Athena bought? (Give the answer in inches.)
19. Linda Johanssen had quarts of liquid fertilizer in a container. Her supervisor asked her to mix of
the fertilizer with water and save the remainder. How many quarts of fertilizer did Linda mix with
water?
20. Landscaper Roger Hillman needs several pieces of PVC irrigation pipe, each 3 feet 4 inches long. PVC
pipe comes in 20-foot lengths. How many pieces can Roger cut out of one length of pipe? (Hint: 4 inches
equal foot.)
21. Robert Burke has a diesel-powered generator on his ranch. The generator has a tank that holds gallons
of diesel fuel. He stores the diesel fuel in 55-gallon drums (barrels). How many times can Robert refill his
generator from one drum of fuel?
22. Home builders Bill and John Walter are planning a narrow stairway to an attic. The stairs will each be
2 feet 8 inches long. They will cut the stairs from boards that are 8 feet long. How many whole stairs can
they cut from one 8-foot board? (Hint: 8 inches is foot.)
Score for C (36)
2
3
3
3
4
1
3
2
3
2
1
4
6
3
4
2
1
2
5
1
3
2
1
3
4 1
3
4
53
1
3
4
4
5
5
46 Part 1 Fundamental Review
Assignment 2.2 Continued
4
1
6
1
1
3
2
1
2
3 5
1
3
5
5
2
3
16
3
5
5 3 8
1 3 3
5
40
3
5 13
1
3
cu yd
8 3 6
3
4
5
8
1
3
27
4
5
2 3 27
1 3 1
5
54
1
5 54 in.
2
3
of 2
1
4
5
2
3
3 2
1
4
5
2
3
3
9
4
5
1 3 3
1 3 2
5
3
2
5 1
1
2
qt
20 4 3
1
3
5
20
1
4
10
3
5
20
1
3
3
10
5
2 3 3
1 3 1
5
6
1
5 6 pieces
55 4 3
3
4
5
55
1
4
15
4
5
55
1
3
4
15
5
11 3 4
1 3 3
5
44
3
5 14
2
3
8 4 2
2
3
5
8
1
4
8
3
5
8
1
3
3
8
5
1 3 3
1 3 1
5 3 stairs
13
1
3
cu yd
1
1
2
qt
14
2
3
times
3 stairs
6 pieces
54 in.
7
3
4
7
4
5
7
3
3
4
7
5
1 3 4
3 3 1
5
4
3
5 1
1
3
10
3
4
4
5
5
10
3
3
5
4
5
5 3 5
3 3 2
5
25
6
5 4
1
6
Decimals
Chapter 3 Decimals 47
Learning Objectives
By studying this chapter and completing all assignments, you will be able to:
Learning Objective
Read decimal numbers.
Learning Objective
Round decimal numbers.
Learning Objective
Add two or more decimal numbers.
Learning Objective
Subtract one decimal number from another.
Learning Objective
Multiply two decimal numbers.
Learning Objective
Divide one decimal number by another decimal number.
Learning Objective
Multiply and divide by decimal numbers that end with zeros.
Learning Objective
Approximate products and quotients.
3
1
Learning Objective
2
Learning Objective
3
Learning Objective
4
Learning Objective
5
Learning Objective
6
Learning Objective
7
Learning Objective
8
Learning Objective
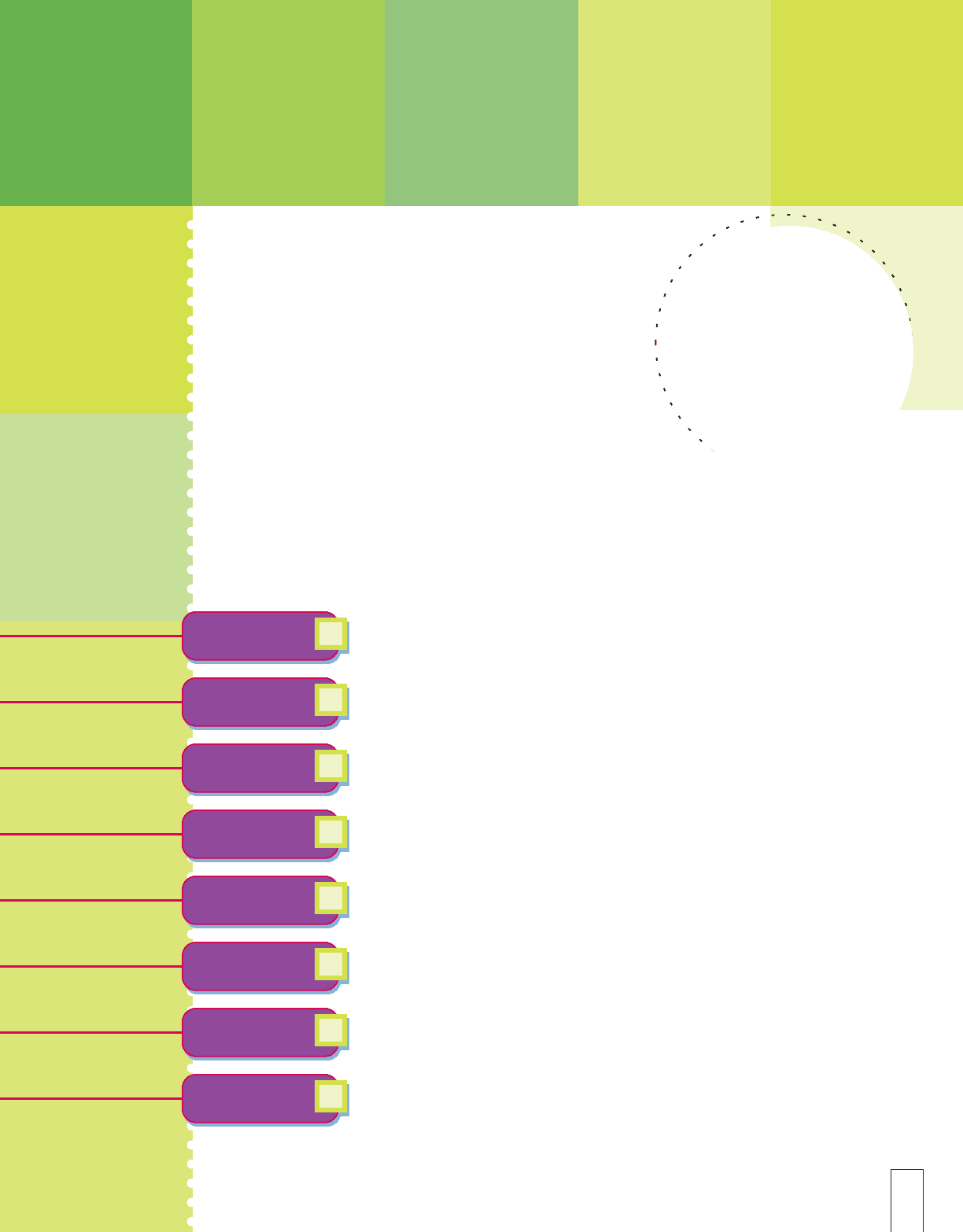
McDonald’s restaurant sells a hamburger sandwich called the Quarter
Pounder. The sandwich is named for the amount of meat: one-quarter
pound of ground beef. McDonald’s—or anyone—can describe the same
amount of meat in four different ways: 4 ounces, pound, 0.25 pound, or
25% of a pound. To express less than 1 pound, McDonald’s could use smaller
units, fractions, decimals, or percents.
All four expressions are useful, but which one is best? It may depend on
what you’re doing: whether you’re buying or selling, whether you’re speaking
or writing, whether you’re just estimating or making accurate financial
records, or whether you’re working with large volumes of something cheap or
small quantities of something very expensive. For McDonald’s, a Four Ouncer
might not sell as well as a Quarter Pounder, but Bloomingdale’s sells perfume
by the (fluid) ounce rather than by the gallon, quart, pint, or even cup.
Verbal expressions such as “half of a candy bar” or “a third of the pizza” are so common
that children learn them before they can even read. We reviewed fractions in Chapter 2.
Because of calculators, most calculations are now performed using decimal numbers. We
review decimals here in Chapter 3. Percents are a combination of decimal numbers and a
few common fractions. Percents are as easy to use as decimals and also allow simple verbal
expressions. We review percents in Chapter 5.
Chapter 3 has three main concepts: vocabulary, calculating, and estimating. Calculat-
ing with decimals is the same as with whole numbers except that there is a decimal
point. Thus, calculating with decimals is actually “managing the decimal point,” which
your calculator does automatically. Estimating, which is important in checking your cal-
culations, still requires that you “manage the decimal point.”
A customer in a delicatessen might ask for “a quarter of a pound of salami, please” or
perhaps “four ounces of salami.” However, the food scale in the delicatessen probably has
an electronic display and is calibrated only in pounds. It will likely display “0.25” or
“0.250.” As a fraction, a quarter of a pound is written as pound; three quarters of a
pound is pound. In the U.S. monetary system, a quarter is the name of the coin whose
value is twenty-five cents. And three quarters are worth seventy-five cents. When we
write these monetary amounts, we write either whole numbers or decimals: 25¢ and 75¢,
or $0.25 and $0.75. It is highly unlikely that anyone would ever write $ or $ .
Almost all business transactions and record keeping are best done using decimals
rather than fractions. The calculations are usually more straightforward and more accu-
rate. Today, specialized calculators, computers, and measurement instruments have elec-
tronic displays that are calibrated in decimals, not fractions.
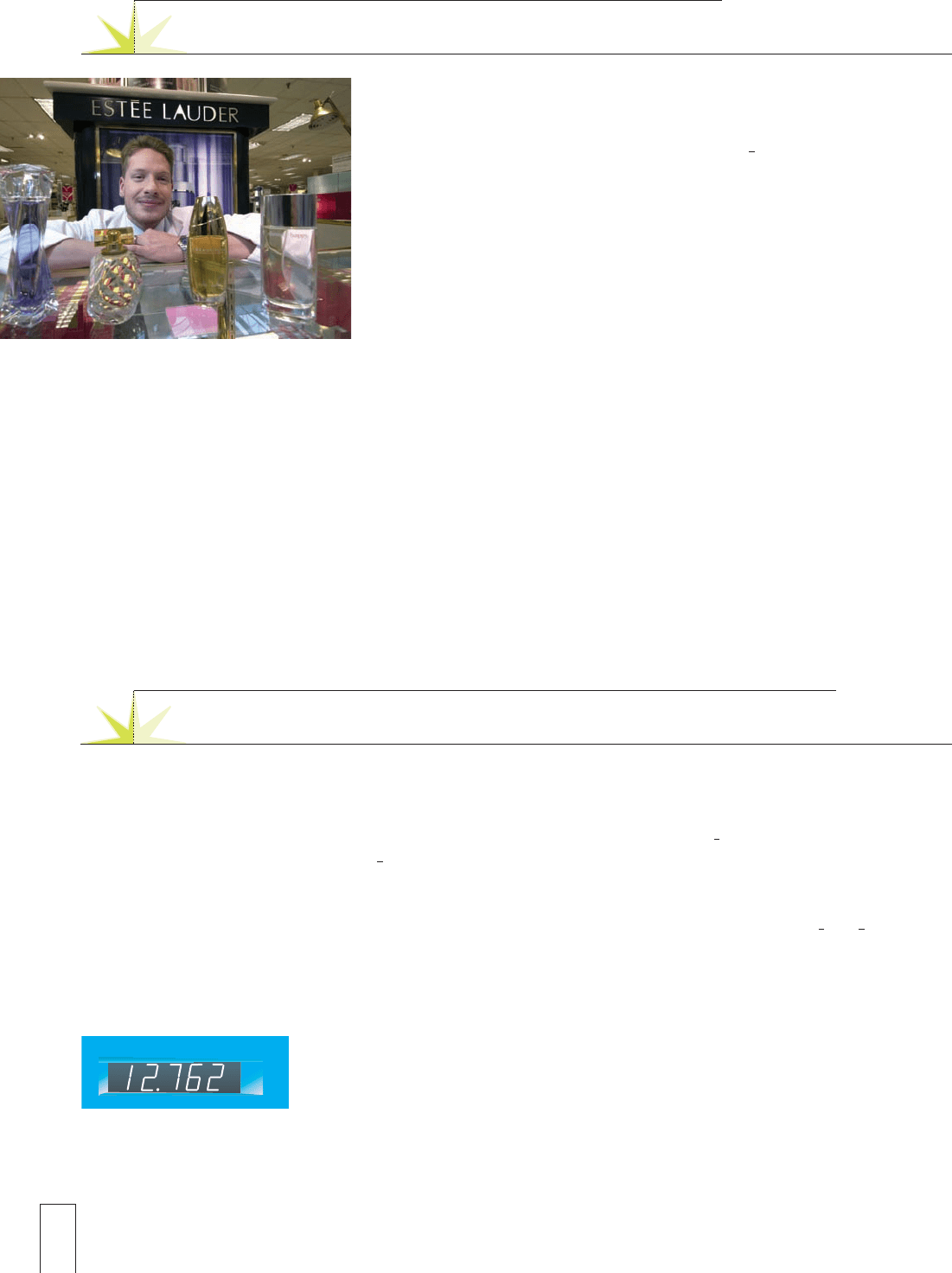
Modern gasoline pumps used in the United States are calibrated in gallons and typi-
cally measure the volume of gasoline sold accurate to three decimal places. Suppose that
an automobile owner buys gasoline and the display shows 12.762 gallons. 12.762 is a
number; it is called a mixed decimal. The 12 is the whole number part of the number;
the 762 is the pure decimal part. The period (or dot) that separates the 12 from the 762
3
4
1
4
3
4
1
4
1
4
48 Part 1 Fundamental Review
Fractions Versus Decimal Numbers
Decimal Numbers and Electronic Displays
© DOUG KOONTZ/THE (FREDERICK) NEWS-
POST/ASSOCIATED PRESS
Gallons
is the decimal point. We say that the number 12.762 has three decimal places because
there are three digits to the right of the decimal point.
Many calculators and all computer spreadsheets permit you to change the number of
decimal places that are displayed. A new calculator may be preset to display exactly two
decimal places because that is how the monetary system is designed. Divide 1 by 3 with
your calculator. The correct answer is 0.333333333 ...repeating number that never
stops. Count the number of 3s that appear in the calculator. That is the number of deci-
mal places your calculator is set to display. Read the instruction manual. Perhaps you can
change the display to show more or fewer decimal places. Note: Your calculator also dis-
plays a zero (0) to the left of the decimal point. We follow that same convention in this
book. Every pure decimal number is preceded by a zero (0).
Chapter 3 Decimals 49
Reading decimal numbers, both mixed and pure, is like reading whole numbers: Each
“place,” or column, represents a different value. Starting at the decimal point and read-
ing to the left, the places represent ones, tens, hundreds, thousands, and so on. Starting
at the decimal point and reading to the right, the vocabulary is different: The places rep-
resent tenths, hundredths, thousandths, and so on.
Recall words such as tenths, hundredths, and thousandths from your review of frac-
tions in Chapter 2. As money, the decimal $0.10 represents 10¢, but also . is pro-
nounced as “ten hundredths.” But can be reduced to which is “one tenth.” Like
fractions, the decimal 0.10 is read as “ten hundredths”; the decimal 0.1 is “one tenth.”
At the gasoline pump, the display showed 12.762. As a fraction, it is written . Both
numbers are pronounced “twelve and seven hundred sixty-two thousandths. The deci-
mal point is read as the word “and.”
Figure 3-1 illustrates the place values of the number system on both sides of the
decimal point for the number 607,194.35824. The pure decimal part of the number in
Figure 3-1 is 0.35824, which is pronounced “thirty-five thousand eight hundred twenty-
four hundred-thousandths.”
12
762
1000
1
10
10
100
10
100
$
10
100
Reading Decimal Numbers
Read decimal numbers.
1
Learning Objective
Figure 3-1 Number System on Both Sides of the Decimal Point
4 ones
9 tens
1 hundred
7 thousands
0 ten thousands
6 hundred thousands
3 tenths
5 hundredths
8 thousandths
2 ten-thousandths
4 hundred-thousandths
607,194.35824
READING LONG DECIMAL NUMBERS
The entire number in Figure 3-1—607,194.35824—is read as “six hundred seven thou-
sand, one hundred ninety-four and thirty-five thousand eight hundred twenty-four
hundred-thousandths.” For a long number, reciting it orally is inefficient and can be
confusing to the listener. For such a number, it may be better simply to read the digits
and commas, from left to right. The word point is used for the decimal point.
3.1 The U.S.system for weight is not a
pure decimal system.Post office scales
are typically in pounds and ounces.
However,grocery store scales are typi-
cally in pounds and tenths of pounds.
Therefore,some people may be tem-
porarily confused as they move from
scale to scale.
3.2 When numbers are written,the
word and is used only to indicate a
decimal point.But in spoken English,
people commonly use the word and
in other ways, as in “one hundred and
fifty dollars.”Often the word and is
slurred so that the phrase sounds like
“one hundred’n fifty.”This inconsis-
tency of usage is why, when accuracy is
important,it makes sense to read
numbers orally by saying each digit
and using the word point to indicate
the decimal point.
3.3 Remind students that commas are
not used to the right of the decimal
point.
3.4 You might want to mention that
Europeans write a comma instead of
a period for the decimal point and a
period to separate hundreds from
thousands.Also,some calculators
permit you to select either notation
system.
EXAMPLE A
Recite orally the number 607,194.35824.
Number Oral Recitation
607,194.35824 “six zero seven comma one nine four point three five eight two four”
50 Part 1 Fundamental Review
✔
CONCEPT CHECK 3.1
a. Write 37.045 using words: Thirty-seven and forty-five thousandths
b. Write fifteen and seven hundredths using digits: 15.07
In the preceding section, you reviewed how to read and write decimal numbers such as
148.65392. However, in many business situations, if the whole number part is as large as
148, the digits on the extreme right may not be very important. Maybe only the digit in
the tenths or hundredths column is significant. Rounding off such a number to make it
simpler is common. You rounded off whole numbers in Chapter 1. The procedure is the
same with decimal numbers.
Rounding Decimal Numbers
2
Learning Objective
Round decimal numbers.
to Round Decimal Numbers
1. Find the last place, or digit, to be retained.
2. Examine the digit to the right of the last digit to be retained.
3. a. If it is equal to or greater than 5, increase the digit to be retained by 1.
Drop all digits to the right of the ones retained.
b. If it is less than 5, leave the digit to be retained unchanged. Drop all
digits to the right of the ones retained.
STEPS
EXAMPLE B
Round 7.3951 and 148.65392 to one decimal place, to two decimal places, and to three
decimal places.
Round to the nearest tenth 7.3
951 7.4 148.65392 148.7
Round to the nearest hundredth 7.39
51 7.40 148.65392 148.65
Round to the nearest thousandth 7.3951 7.395 148.65392 148.654
3.5 At the post office,weights are
essentially rounded up.Currently,a
1-ounce letter costs 42¢,and a 2-ounce
letter costs 59¢.Any letter between 1
and 2 ounces also costs 59¢.A weight
of only 1.05 ounces costs the same as
a weight of 2 ounces.
When lumber is sold by the linear
foot,a 711 board cannot be sold as
an 8 board.It could be “rounded
down”and sold as a 7 board.If you
need 8 boards to build a house,711
is not long enough.Rounding down is
also called truncating.
Mention that many calculators
will round off to a specified number of
decimal places.The calculator will not
round off whole numbers,however.
For example,it will not round to the
nearest hundred or thousand.Some
calculators may truncate decimals
rather than round them off.
ROUNDING UP
Retail businesses, such as grocery stores, often use a different method of rounding to a
whole number of cents. Suppose that a grocery store has lemons priced at 3 for $1.00.
Usually the store will charge $0.34 for one lemon, even though $1.00 divided by 3 is
$0.3333 (to four places). The store has rounded up to the next larger whole cent. To
round up monetary amounts, always increase any partial cent to the next whole cent.
For example, $27.842 would round up to $27.85.

Chapter 3 Decimals 51
✔
CONCEPT CHECK 3.2
a. Round 3.4681 to the nearest hundredth (that is, to two decimal places).
Find the hundredths digit. 3.4681 (The 6)
Examine the digit to the right of the 6. 3.4681 (It is greater than 5.)
Increase the 6 to a 7 and drop the digits 3.47 (The answer)
81 at the right.
b. Round up 8.5014 to the next tenth (that is, to one decimal place).
Find the tenths digit. 8.5014 (The 5)
Increase the 5 to a 6 and drop the 8.6 (The answer)
digits 014 at the right.
In Chapter 1, we reviewed arithmetic with whole numbers. There were also some prob-
lems involving money in which the numbers contained decimal points. A whole number
is simply a mixed decimal where the pure decimal part is zero. For simplicity, the zeros
and the decimal point are omitted. In the examples that follow, when you see a whole
number, you may need to place a decimal point at the right end and maybe even write
one or more zeros after it. As you calculate, “manage the decimal point” as described in
the following sections.
Whole Numbers, Decimal Numbers,
and Arithmetic
To add two or more decimal numbers, follow these steps.
Adding Decimal Numbers
Add two or more decimal numbers.
3
Learning Objective
to Add Decimal Numbers
1. Arrange the numbers in columns, with the decimal points in a vertical
line.
2. Add each column, from right to left, as with whole numbers. Insert the
decimal point.
Option: You may want to write zeros in some of the right-hand columns of
decimal numbers so that each number has the same number of
decimal places.
STEPS
© R. ALCORN/CENGAGE LEARNING
Subtracting one decimal number from another is similar to subtracting whole numbers.
When you aren’t using a calculator, it may be helpful to write enough zeros so that both
numbers have the same number of places. To subtract one decimal number from an-
other, follow these steps.
EXAMPLE C
Add 4.326, 218.6004, 7.09, 15, and 0.87782.
4.326 4.326 4.32600
218.6004 218.6004 218.60040
7.09 7.09 or 7.09000
15. 15. 15.00000
0.87782 0.87782 0.87782
245.89422 245.89422
STEP 2 WITH OPTIONSTEP 2STEP 1
52 Part 1 Fundamental Review
Add these decimal numbers: 8.95, 13.791, and 0.6.
First align: Then add: Or, write zeros and add:
8.95 8.95 8.950
13.791 13.791 13.791
0.6 0.6 0.600
23.341 23.341
✔
CONCEPT CHECK 3.3
Subtracting Decimal Numbers
4
Learning Objective
Subtract one decimal number from
another.
to Subtract Decimal Numbers
1. Arrange the numbers in columns, with the decimal points in a vertical
line.
2. If necessary, write enough extra zeros so that both numbers have the
same number of decimal places.
3. Subtract each column, from right to left, as with whole numbers. Insert
the decimal point.
STEPS
EXAMPLE D EXAMPLE E
Subtract 4.935 from 12.8. Subtract 9.4 from 82.113.
12.8 12.800 82.113 82.113
4.935 4.935 9.4 9.400
7.865 72.713
STEPS 2 & 3STEP 1STEPS 2 & 3STEP 1

To multiply one decimal number by another, follow these steps.
Chapter 3 Decimals 53
Subtract 53.784 from 207.6.
Align: Write zeros and subtract:
207.6 207.600
53.784 53.784
153.816
COMPLETE ASSIGNMENT 3.1.
✔
CONCEPT CHECK 3.4
Multiplying Decimal Numbers
Multiply two decimal numbers.
5
Learning Objective
to Multiply Decimal Numbers
1. Multiply the two numbers as if they were whole numbers.
2. Count the total number of decimal places in the two original numbers.
3. a. In the product, place the decimal point so that the number of
decimal places is the same as the number in Step 2. (Count from right
to left.)
b. If necessary, insert zeros in front of the left-hand digit to provide
enough decimal places. (See example G.)
STEPS
EXAMPLE F EXAMPLE G
3.764 2.1 3.764 0.0021
3.764 (3 places) 3.764 (3 places)
.. 2.1 (1 place) 0.0021 (4 places)
3764 3764
7528 0 0 0 7528 0 0
7.9044 (3 1 4 places) 0.0079044 (3 4 7
places; insert
2 zeros)
STEP 3STEP 3
STEP 2STEP 2
STEP 1STEP 1
In business applications, zeros that come at the right end of the decimal part of the
product are often omitted (example H). Do not omit zeros that come at the end of the
whole-number part (example I). When the product is written in dollars and cents, exactly
two decimal places are written, including zeros at the right end (example J). Please be
aware that some calculators may not display any zeros at the right end of a decimal.
3.6 Review with students how to set
the number of decimal places on their
calculators.This setting will dictate
how many zeros the calculator displays
at the end of a decimal.
