De Felice F., Bini D. Classical Measurements in Curved Space-Times
Подождите немного. Документ загружается.

5.4 The world function in de Sitter space-time 83
where x
i
0
are integration constants and σ is a sign indicator, corresponding to
future-pointing (σ = 1) or past-pointing (σ = −1) geodesics, and the null case
= 0 is intended in the sense of the limit.
Let us require now that s = 0 corresponds to the space-time point A and s =1
to B. This implies
e
H
0
t
A
=
C
√
sin[
√
α
0
],e
H
0
t
B
=
C
√
sin[
√
(σH
0
+ α
0
)],
x
i
A
− x
i
0
= −
C
i
C
2
σH
0
√
cot[
√
α
0
],
x
i
B
− x
i
0
= −
C
i
C
2
σH
0
√
cot[
√
(σH
0
+ α
0
)]. (5.54)
Moreover, from (5.2)
L =
!
1
0
||ds =
|| (5.55)
and, from (5.3),
Ω(X
A
,X
B
)=
1
2
||. (5.56)
Using relations (5.54) one can then obtain as a function of the coordinates of
A and B, and hence Ω. To this end it is convenient to write down an equivalent
set of equations in place of (5.54) namely
√
α
0
=arcsin
√
C
e
H
0
t
A
,
√
σH
0
=arcsin
√
C
e
H
0
t
B
− arcsin
√
C
e
H
0
t
A
,
ξ
2
≡ δ
ij
(x
i
B
− x
i
A
)(x
j
B
− x
j
A
)
=
C
2
H
2
0
[cot[
√
(σH
0
+ α
0
)] −cot[
√
α
0
]]
2
, (5.57)
in the three unknowns α
0
,C
2
,and. Using the the first two of these equations
in the third one gives
H
2
0
ξ
2
=
C
2
cot
arcsin
√
C
e
H
0
t
B
− cot
arcsin
√
C
e
H
0
t
A
2
, (5.58)
which can be formally inverted to obtain the quantity
√
/C in terms of
t
A
,t
B
,x
i
A
,x
i
B
. To see this in detail let us use the notation
w =
√
/C, a = e
H
0
t
A
,b= e
H
0
t
B
; (5.59)
we then have
H
2
0
ξ
2
= w
2
1
b
2
w
2
− 1 −
1
a
2
w
2
− 1
2
, (5.60)

84 The world function
from which
w
2
=
[(a + b)
2
− H
2
0
ξ
2
a
2
b
2
][H
2
0
ξ
2
a
2
b
2
− (a −b)
2
]
4ξ
2
a
4
b
4
H
2
0
. (5.61)
Back-substituting this expression for w =
√
/C in the second of Eqs. (5.57) then
gives ,
√
=
1
σH
0
[arcsin(bw) −arcsin(aw)], (5.62)
and hence Ω, from (5.56).
5.5 The world function in G¨odel space-time
In Cartesian-like coordinates x
α
=(t, x, y, z), G¨odel’s metric takes the form
(2.133) that we recall here (G¨odel, 1949):
ds
2
= −dt
2
+ dx
2
−
1
2
U
2
dy
2
− 2Udtdy + dz
2
, (5.63)
where U = e
√
2ωx
and ω is a constant. The symmetries of this metric are sum-
marized by five Killing vector fields,
ξ
μ
t
= ∂
t
,ξ
μ
y
= ∂
y
,ξ
μ
z
= ∂
z
,ξ
μ
4
= ∂
x
−
√
2ωy∂
y
,
ξ
μ
5
= −2e
−
√
2ωx
∂
t
+
√
2ωy∂
x
+(e
−2
√
2ωx
− ω
2
y
2
)∂
y
. (5.64)
Let us consider a geodesic Υ parameterized by an affine parameter λ with tan-
gent vector P
μ
=(
˙
t, ˙x, ˙y, ˙z), where dot means differentiation with respect to λ.
The geodesic equations are
¨
t +2
√
2ω
˙
t ˙x +
√
2ωU ˙x ˙y =0,
¨x +
√
2ωU
˙
t ˙y +
1
2
U
2
√
2ω ˙y
2
=0,
¨y − 2
√
2ωU
−1
˙
t ˙x =0,
¨z =0. (5.65)
Using the Killing symmetries, this system of equations can be fully integrated.
First we recall that
p
t
= g
tα
dx
α
dλ
≡−E = constant,
p
y
= g
yα
dx
α
dλ
≡ p
y
= constant, (5.66)
p
z
=
dz
dλ
≡ p
z
= constant

5.5 The world function in G¨odel space-time 85
are conserved quantities. Then, from the above and the metric form (5.63), it
follows that
˙
t = −E −
2p
y
U
, ˙y =
2E
U
+
2p
y
U
2
, (5.67)
and
z(λ)=z
0
+ p
z
λ. (5.68)
Using these relations in (5.65) we obtain
¨x −
2
√
2ωEp
y
U
−
2
√
2ωp
2
y
U
2
=0. (5.69)
Multiplying both sides of (5.69)by2˙x we can write it as
d
dλ
˙x
2
+4Ep
y
e
−
√
2ωx
+2p
2
y
e
−2
√
2ωx
=0, (5.70)
which implies that
˙x
2
+4Ep
y
e
−
√
2ωx
+2p
2
y
e
−2
√
2ωx
= C
1
, (5.71)
where C
1
is a constant. The normalization condition p·p = −, with =(1, 0, −1)
for time-like, null, and space-like orbits respectively, allows one to fix the constant
C
1
as
C
1
= −
2
− E
2
− p
2
z
; (5.72)
then Eq. (5.71) can be integrated by standard methods. Use of this solution in
both Eqs. (5.67) leads us to the full integration of the geodesic equations. Clearly
this allows us to write the exact world function along any non-null geodesic.
In a remarkable paper, Warner and Buchdahl (1980) were able to derive the
exact form of the world function for G¨odel’s space-time, following an alternative
approach. Their aim was to find the world function as a solution of a set of
differential equations. Following their arguments, let us first recall from (5.39)
that, given a set of Killing vectors ξ
(a)
and a pair of events with coordinates {x
μ
}
and {x
μ
}, the world function satisfies the relation
ξ
μ
(a)
∂
μ
Ω+ξ
μ
(a)
∂
μ
Ω=0. (5.73)
We then have
∂
t
Ω+∂
t
Ω=0,
∂
y
Ω+∂
y
Ω=0,
∂
z
Ω+∂
z
Ω=0, (5.74)
which imply for Ω a dependence of the type
Ω(t
− t, x, x
,y
− y,z
− z;Υ)= Ω
1
(τ,x,x
,ξ;Υ)+
1
2
(z
− z)
2
, (5.75)

86 The world function
where Ω
1
is a new function to be determined and
τ = t
− t, ξ = y
− y. (5.76)
Using the remaining Killing vectors ξ
(4)
and ξ
(5)
we have from (5.64) the addi-
tional equations
0=∂
x
Ω −
√
2ωy∂
y
Ω+∂
x
Ω −
√
2ωy
∂
y
Ω, (5.77)
0=
√
2ωy∂
x
Ω+(e
−2
√
2ωx
− ω
2
y
2
)∂
y
Ω −2e
−
√
2ωx
∂
t
Ω
+
√
2ωy
∂
x
Ω+(e
−2
√
2ωx
− ω
2
y
2
)∂
y
Ω
−2e
−
√
2ωx
∂
t
Ω. (5.78)
Introducing the new variables
v = e
−
√
2ωx
,v
= e
−
√
2ωx
, (5.79)
and recalling (5.75), Eq. (5.77) gives
v∂
v
Ω
1
+ v
∂
v
Ω
1
+ ξ∂
ξ
Ω
1
=0, (5.80)
whose solution is
Ω
1
=Ω
1
τ,
v
ξ
,
v
ξ
. (5.81)
Using this form of Ω
1
in (5.78) and denoting
α =
v
ξ
,β=
v
ξ
, (5.82)
we obtain
α(ω
2
− β
2
+ α
2
)∂
α
Ω
1
− β(ω
2
− α
2
− β
2
)∂
β
Ω
1
+2(α − β)∂
τ
Ω
1
=0. (5.83)
This equation can be considerably simplified with the further change of variables
s + r =
α
ω
,s− r =
β
ω
,τ
1
= ωτ, (5.84)
leading to
s(4r
2
+1)∂
r
Ω
1
+ r(4s
2
+1)∂
s
Ω
1
+4r∂
τ
1
Ω
1
=0. (5.85)
This equation can be solved with the method of separation of variables. Setting
Ω
1
=Ω
1
(r)+Ω
1
(s)+Ω
1
(τ
1
), we obtain
Ω
1
=
1
8
Kln
4r
2
+1
4s
2
+1
+
¯
K
1
2
tan
−1
(2s) −τ
1
, (5.86)
where K and
¯
K are separation constants. Hence the full world function (5.75)
follows.

5.6 The world function of a weak gravitational wave 87
5.6 The world function of a weak gravitational wave
Consider the metric of a weak gravitational plane wave propagating along the x
direction of a coordinate frame with “+, ×” polarization states, written in the
form
ds
2
= −dt
2
+ dx
2
+(1− h
+
)dy
2
+(1+h
+
)dz
2
− 2h
×
dxdz, (5.87)
where the wave amplitudes h
+/×
= h
+/×
(t−x) are functions of (t−x). Let them
be given by
h
+
= A
+
sin ω(t − x),h
×
= A
×
cos ω(t − x), (5.88)
where linear polarization is characterized by A
+
=0orA
×
= 0, whereas circular
polarization is assured by the condition A
+
= ±A
×
. It is also useful to introduce
the polarization angle, ψ = tan
−1
(A
×
/A
+
).
The geodesics of this metric are given by (de Felice, 1979)
U
(geo)
=
1
2E
[(
2
+ f + E
2
)∂
t
+(
2
+ f −E
2
)∂
x
]
+[α(1 + h
+
)+βh
×
]∂
y
+[β(1 − h
+
)+αh
×
]∂
z
, (5.89)
where α, β,andE are conserved Killing quantities,
2
=1, 0, −1 correspond to
time-like, null, and space-like geodesics respectively, and to first order in the wave
amplitudes
f α
2
(1 + h
+
)+β
2
(1 −h
+
)+2αβh
×
. (5.90)
The parametric equations of the geodesics are then easily obtained:
t(λ)=Eλ + t
0
+ x(λ) −x
0
,
x(λ)=(
2
+ α
2
+ β
2
− E
2
)
λ
2E
−
1
2ωE
2
[(α
2
− β
2
)A
+
cos ω(Eλ + t
0
− x
0
)
−2αβA
×
sin ω(Eλ + t
0
− x
0
)] + x
0
,
y(λ)=αλ + y
0
−
1
ωE
[αA
+
cos ω(Eλ + t
0
− x
0
) −βA
×
sin ω(Eλ + t
0
− x
0
)],
z(λ)=βλ + z
0
+
1
ωE
[βA
+
cos ω(Eλ + t
0
− x
0
)+αA
×
sin ω(Eλ + t
0
− x
0
)] , (5.91)
where λ is an affine parameter and x
0
,y
0
,z
0
are integration constants.
We can then evaluate the world function for two general points
P
0
and P
1
connected by a geodesic Υ. A direct calculation gives
Ω(s
0
,s
1
;Υ)=Ω(s
0
,s
1
)
flat
+
A
+
2ω
[(y
1
− y
0
)
2
− (z
1
− z
0
)
2
]
cos ω(t
1
− x
1
) −cos ω(t
0
− x
0
)
t
1
− x
1
− (t
0
− x
0
)
−
A
×
ω
(y
1
− y
0
)(z
1
− z
0
)
sin ω(t
1
− x
1
) −sin ω(t
0
− x
0
)
t
1
− x
1
− (t
0
− x
0
)
, (5.92)

88 The world function
where
Ω(s
0
,s
1
)
flat
=
1
2
η
αβ
(x
0
− x
1
)
α
(x
0
− x
1
)
β
(5.93)
is the world function in Minkowski space-time (see Bini et al., 2009).
5.7 Applications of the world function: GPS or emission
coordinates
Let us briefly review the standard construction of GPS coordinates in a flat
space-time (Rovelli, 2002). Consider Minkowski space-time in standard Cartesian
coordinates (t, x, y, z),
ds
2
= η
αβ
dx
α
dx
β
= −dt
2
+ dx
2
+ dy
2
+ dz
2
, (5.94)
and four satellites, represented by test particles in geodesic motion. With the
above choice of coordinates, time-like geodesics are straight lines:
x
α
A
(τ
A
)=U
α
A
τ
A
+ x
α
A
(0), A =1,...,4, (5.95)
where
U
A
= γ
A
[∂
t
+ ν
A
n
i
A
∂
i
]=coshα
A
∂
t
+sinhα
A
n
i
A
∂
i
(5.96)
are their (constant) 4-velocities and τ
A
is the proper time parameterization along
each world line. In (5.96), γ
A
is the Lorentz factor and the linear velocities ν
A
are
relative to any of the four particles chosen as a fiducial observer; they are related
to the rapidity parameters α
A
by ν
A
= tanh α
A
; n
A
denotes the space-like unit
vectors along the spatial directions of motion. Without any loss of generality,
we assume that the satellites all start moving from the origin of the coordinate
system O, so hereafter we set x
α
A
(0) = 0, and hence
x
α
A
(τ)=U
α
A
τ
A
. (5.97)
Let us now consider a general space-time point
¯
P with coordinates
¯
W
α
and a
point P
A
with coordinates x
α
A
on the world line of the Ath satellite corresponding
to an elapsed amount of proper time τ
A
. A photon emitted at P
A
follows a null
geodesic, i.e. the straight line
x
α
(λ)=K
α
λ + x
α
A
, (5.98)
where λ is an affine parameter. Such a photon will reach
¯
P at a certain value
¯
λ
of the parameter according to
¯
W
α
= K
α
¯
λ + x
α
A
, (5.99)
implying that
U
α
A
τ
A
−
¯
W
α
= −K
α
¯
λ. (5.100)
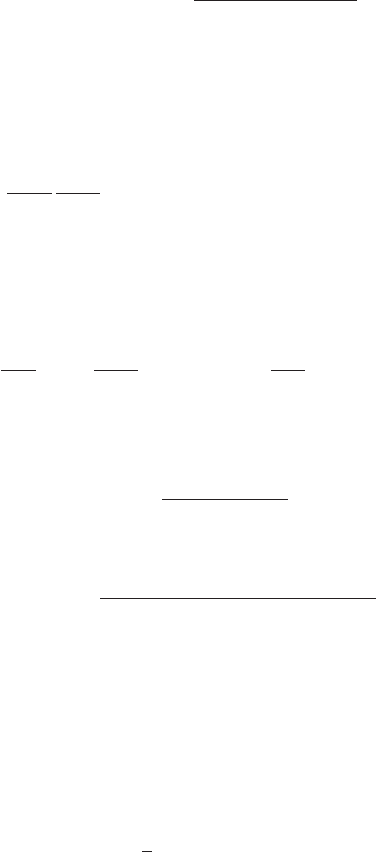
5.7 Applications of the world function: GPS or emission coordinates 89
Taking the norm of both sides, we obtain
− (τ
A
)
2
+ ||
¯
W ||
2
− 2τ
A
(U
A
·
¯
W )=0, (5.101)
since K is a null vector. Solving for τ
A
and selecting the solution corresponding
to the past light cone leads to
τ
A
= −(U
A
·
¯
W ) −
(U
A
·
¯
W )
2
+ ||
¯
W ||
2
. (5.102)
These equations give the four proper times τ
A
(i.e. the GPS or emission coordi-
nates) associated with each satellite in terms of the Cartesian coordinates of the
general point
¯
P in the space-time, i.e. τ
A
= τ
A
(
¯
W
0
,...,
¯
W
3
).
Using Eq. (5.102), one can evaluate the inverse of the transformed metric
g
AB
= η
αβ
∂τ
A
∂
¯
W
α
∂τ
B
∂
¯
W
β
≡ η
αβ
(dτ
A
)
α
(dτ
B
)
β
= dτ
A
· dτ
B
, (5.103)
where the dual frame (dτ
A
)
α
= ∂τ
A
/∂
¯
W
α
also satisfies the properties
(dτ
A
)
α
¯
W
α
= τ
A
, (dτ
A
)
α
U
α
A
=1. (5.104)
Similarly one can introduce the frame vectors
∂
∂τ
A
α
=
∂
¯
W
α
∂τ
A
, (dτ
A
)
α
∂
∂τ
B
α
= δ
A
B
. (5.105)
It is then easy to show that the condition g
AA
= dτ
A
· dτ
A
= 0 is fulfilled. In
fact, by differentiating both sides of Eq. (5.101) with respect to
¯
W
α
one obtains
(dτ
A
)
α
=
¯
W
α
− τ
A
U
Aα
τ
A
+(U
A
·
¯
W )
, (5.106)
which implies that
g
AA
=(dτ
A
)
α
(dτ
A
)
α
=
−(τ
A
)
2
+ ||
¯
W ||
2
− 2τ
A
(U
A
·
¯
W )
[τ
A
+(U
A
·
¯
W )]
2
=0. (5.107)
The metric coefficients g
AB
=(∂/∂τ
A
) ·(∂/∂τ
B
)=η
αβ
(∂/∂τ
A
)
α
(∂/∂τ
B
)
β
can
be easily obtained as well by expressing the Cartesian coordinates of
¯
P in terms
of the emission coordinates τ
A
, i.e.
¯
W
α
=
¯
W
α
(τ
1
,...,τ
4
).
To accomplish this, it is enough to invert the transformation (5.102). However,
in order to outline a general procedure, we start by considering the equation for
the past light cone of the general space-time point
¯
P with coordinates
¯
W
α
given in
terms of the world function, which in the case of flat space-time is simply given by
Ω
flat
(x
A
,x
B
)=
1
2
η
αβ
(x
α
A
− x
α
B
)(x
β
A
− x
β
B
). (5.108)
The condition ensuring that the past light cone of
¯
P cuts the emitter world lines
is given by
Ω
flat
(x
A
,
¯
W )=0,x
0
A
<
¯
W
0
, (5.109)
90 The world function
for each satellite labeled by the index
A. This gives rise to a system of four
quadratic equations in the four unknown coordinates
¯
W
α
of the event
¯
P of the
form (5.101)foreach
A =1,...,4. To solve this system, start for example by sub-
tracting the last equation from the first three equations to obtain the following
system:
Ω
flat
(x
i
,
¯
W ) − Ω
flat
(x
4
,
¯
W )=0=−2
¯
W · (x
i
− x
4
) −(τ
i
)
2
+(τ
4
)
2
,
Ω
flat
(x
4
,
¯
W )=0=||
¯
W ||
2
− 2
¯
W · x
4
− (τ
4
)
2
, (5.110)
with i =1, 2, 3, consisting of three linear equations and only one quadratic equa-
tion. Thus we can first solve the linear equations for the coordinates
¯
W
1
,
¯
W
2
,
¯
W
3
in terms of
¯
W
0
, which then can be determined from the last quadratic equation.
As a result, the coordinates of the event
¯
P are fully determined in terms of the
satellite proper times τ
A
and the known parameters characterizing their world
lines.
An explicit result can easily be obtained for a fixed kinematical configuration
of satellites. As an example one can take one of the satellites at rest at the origin
O and the other three in motion along each of the three spatial directions:
U
1
=coshα
1
∂
t
+sinhα
1
∂
x
,
U
2
=coshα
2
∂
t
+sinhα
2
∂
y
,
U
3
=coshα
3
∂
t
+sinhα
3
∂
z
,
U
4
= ∂
t
, (5.111)
where α
i
, i =1, 2, 3, are the rapidities.
This choice is the one adopted in Bini et al. (2008) to construct emission coordi-
nates in curved space-time (but for the metric associated with Fermi coordinates
around the world line of an accelerated observer) covering a space-time region
around the Earth.

6
Local measurements
The mathematical tools introduced in the previous chapters are essential for
dealing with measurements in curved space-times. Here we shall confine our atten-
tion to local measurements only, i.e. to those whose measurement domain does
not involve space-time curvature explicitly. Given an observer u, the tensorial
projection operators P (u)andT (u) allow one to define the observer’s rest-space
and time dimension in neighborhoods of any of his points which are sufficiently
small to allow one to approximate the measurement domain as a point. The
above operators, in fact, arise naturally as the infinitesimal limit of the non-local
procedure for the measurements of space distances and time intervals, as we will
show.
6.1 Measurements of time intervals and space distances
Let γ be the world line of a physical observer; the parameter s on it is taken to
be the proper time, so the tangent vector field ˙γ is normalized as
˙γ · ˙γ = −1. (6.1)
Here we shall analyze the concepts of spatial and temporal distances between two
events relative to a given observer, referring closely to the analog in Euclidean
geometry.
Consider an event
P not belonging to γ but sufficiently close to it that a normal
neighborhood exists which contains the intersections
A
1
and A
2
of γ with the
generators of the light cone in
P. Referring to Fig. 6.1 we see that all points on γ
between
A
1
and A
2
can be connected to P by a unique non-time-like geodesic which
we shall denote by ζ
s
, with parameter σ.LetA
1
= γ(s
A
1
)andA
2
= γ(s
A
2
). Then
from (5.18) the world function Ω(σ
A
,σ
P
; ζ
s
) along the geodesic ζ
s
connecting a
general point
A = γ(s) with P is given by
Ω(σ
A
,σ
P
; ζ
s
)=
1
2
(σ
P
−σ
A
)
2
˙
ζ
s
·
˙
ζ
s
A
; (6.2)

92 Local measurements
A
2
A
1
P
ζ
s
γ
A(s)
Fig. 6.1. A curve γ is connected to the point P by a light ray emitted at A
1
towards P and recorded at A
2
after being reflected at P. The entire process
takes place in a normal neighborhood U
N
of the space-time.
the geodesics ζ
s
are assumed affine parameterized so (
˙
ζ
s
·
˙
ζ
s
) is constant on them.
Because
P is kept fixed and A is any point on γ : s
A
1
≤ s ≤ s
A
2
, the world function
in (6.2) is only a function of s; hence we write it in general as
Ω(σ(s),σ
P
; ζ
s
) ≡ Ω(s), (6.3)
with the constraints
Ω(s
A
1
)=Ω(s
A
2
)=0. (6.4)
Since γ is a smooth curve, there exists a value s
A
0
: s
A
1
<s
A
0
<s
A
2
at which Ω(s)
has an extreme value, namely at
A
0
= γ(s
A
0
):
dΩ
ds
"
"
"
"
A
0
=0. (6.5)
If
P is sufficiently close to γ then the point A
0
is unique. At A
0
,(6.5) is equiva-
lent to
Ω
α
0
˙γ
α
0
=0, (6.6)
where ˙γ
α
0
≡ ˙γ
α
(s
A
0
) and Ω
α
0
is the derivative at A
0
of the world function along
the geodesic ζ
s
|
A
0
joining A
0
to P and given from (5.29)as
Ω
α
0
= −(σ
P
− σ
A
0
)ξ
α
0
,ξ≡
˙
ζ
s
|
A
0
, (6.7)
where ξ
α
0
= ξ
α
(σ
A
0
). From (6.4) and (6.6) we deduce that
˙γ
α
0
ξ
α
0
=0. (6.8)
