Давнис В.В., Тинякова В.И. Компьютерный практикум по эконометрическому моделированию
Подождите немного. Документ загружается.


12211122
ˆ
)1()
ˆˆ
(
ˆ
−−
−
+
−
=
tttt
aaaa
α
α
, 9,2=t .
2.3. Настройка параметров адаптации путем минимизации критерия
() ()
2
1
2
21
ˆ
3
1
,
−=
∑
tt
yyS αα ,
где
t
y- фактические значения, принадлежащие контрольной выборки (t=10;
11; 12);
t
y
ˆ
- прогнозные значения для моментов времени t=10; 11; 12,
рассчитанные по модели с коэффициентами
19
ˆ
a
и
29
ˆ
a
.
Минимизация
(
)
21
,
α
α
S осуществляется последовательным изменением
параметров адаптации
1
α
и
2
α
в интервале (0; 1) с шагом 0,1.
Все выше описанные расчеты сведены в табл . 7.2.2.
Таблица 7.2.2
Период
y
1
a
2
a
Прогноз
(
)
2
ˆ
yy −
1
936000
936000
9400,00
2
945400
945400
9400,00
3
1058000
1037360
83704,00
4
1010500
1032613
4097,92
5
1023600
1026222
-5341,80
6
1033200
1030736
3528,35
7
1088100
1077333
42289,97
8
1083400
1090645
16209,51
9
1159700
1149131
54258,57
Контрольная выборка
10
1230100
1203389
713456674
11
1361000
1257648
10681643462
12
1523000
1311907
44560450279
Средний квадрат ошибки 55955550415
Стандартная ошибка 136578
В первой строке столбцов
1
a и
2
a находятся начальные значения коэф -
фициентов модели, определенные в соответствии с п. 2.1. В остальных стро -
ках этих столбцов стоят значения текущих значений коэффициентов адаптив-
ной модели, рассчитываемые по формулам п. 2.2.
Оптимальные значения параметров адаптации 8,0
1
=
∗
α ; 9,0
2
=
∗
α .
3. Расчет прогнозных значений по адаптивной модели.
3.1. Последовательный расчет текущих коэффициентов модели
( 12,2=t ) с использованием оптимально настроенных параметров адаптации.
3.2. Расчет прогнозных значений
t
y
ˆ
, (t=13; 14; 15) по модели с теку -
щими коэффициентами для момента t=12.
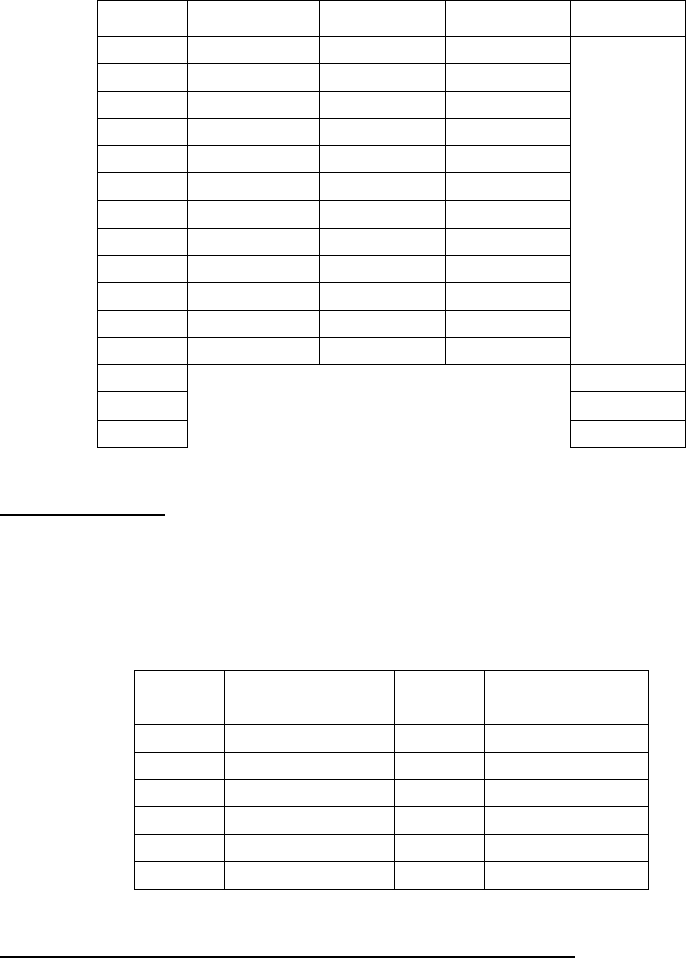
3.3. Оформление результатов расчетов в виде табл . 7.2.3.
Таблица 7.2.3
Период
y
1
a
2
a
Прогноз
1
936000
936000
9400,00
2
945400
945400
9400,00
3
1058000
1037360
83704,00
4
1010500
1032613
4097,92
5
1023600
1026222
-5341,80
6
1033200
1030736
3528,35
7
1088100
1077333
42289,97
8
1083400
1090645
16209,51
9
1159700
1149131
54258,57
10
1230100
1224758
73490,21
11
1361000
1348450
118671,6
12
1523000
1511824
158904,3
13
1670729
14
1829633
15
1988537
Задание 7.2.2. По данным табл . 7.2.4, отражающим объем продаж новых
автомобилей марки Volkswagen в США, построить модель Брауна в виде по-
линома первого порядка . Приняв параметр адаптации
25
,
0
=
α
, осуществить
прогнозные расчеты для
3
=
τ
.
Таблица 7.2.4
Год
Объем продаж ,
шт.
Год
Объем продаж ,
шт.
1988
197200
1994
109600
1989
154900
1995
106600
1990
157500
1996
163200
1991
109000
1997
172000
1992
90500
1998
267200
1993
62100
1999
260286
Решение с помощью табличного процессора Excel.
1. Ввод исходных данных и оформление их в виде таблицы, удобной для
проведения расчетов.
2. Расчет коэффициентов модели.
2.1. Вычисление коэффициентов полинома первой степени
taay
10
+
=
с помощью МНК
76,104788
0
=
a ; 70,7597
1
=
a .
2.2. Определение начальных значений экспоненциальных средних
[
]
1
0
S ,
[
]
2
0
S
[
]
86,12758125,0/)25,01(70,759776,104788
1
0
=−+= S ;
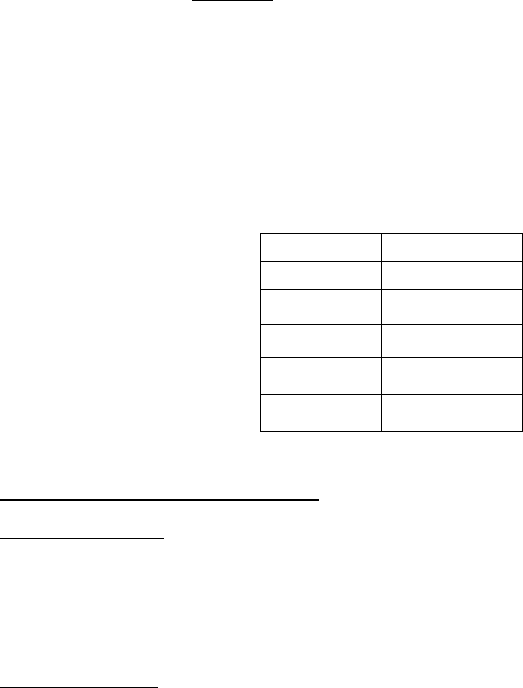
[
]
95,15037425,0/)25,01(270,759776,104788
2
0
=−⋅+= S .
2.3. Вычисление текущих значений экспоненциальных средних
[
]
1
t
S ,
[
]
2
t
S
[
]
39,14498686,127581)25,01(19720025,0
1
1
=⋅−+⋅= S
. . . . . . . . . . . . . . . . . . . . . . . . . .
[
]
77,19127715,168275)25,01(26028625,0
1
12
=⋅−+⋅= S
;
[
]
81,14902786,127581)25,01(39,14498625,0
2
1
=⋅−+⋅= S
. . . . . . . . . . . . . . . . . . . . . . . . . .
[
]
33,15050085,136907)25,01(77,19127725,0
2
12
=⋅−+⋅= S .
2.4. Расчет коэффициентов прогнозного полинома по формулам
21,23205533,15050077,1912772
ˆ
12,0
=
−
⋅
=
a
;
()
48,1359233,15050077,191277
25,01
25,0
ˆ
12,1
=−
−
= a
.
3. Получение прогнозных оценок с помощью полинома
τ
τ
⋅
+
=
+
48,1359221,232055
ˆ
t
y
,
3
,
2
,
1
=
τ
;
259240
ˆ
13
=
y ; 272833
ˆ
14
=
y ; 286425
ˆ
15
=
y .
4. Оформление результатов в виде табл . 7.2.5, 7.2.6
Таблица 7.2.5
Параметр Значение
α
0,25
0
a
104788,76
1
a
7597,70
[
]
1
0
S
127581,86
[
]
2
0
S
150374,95
7. 3. Контрольные задания
Задание 7.3.1. По данным табл . 7.2.4 построить модель Брауна в виде по-
линома второго порядка . Приняв параметр адаптации
25
,
0
=
α
, осуществить
прогнозные расчеты для
3
=
τ
. Сравнить результаты расчетов по моделям
первого и второго порядка .
Задание 7.3.2. По данным табл . 7.3.1 для автомобиля марки Ford постро -
ить две модели: модель Хольта и модель Брауна. Для обеих моделей провести
оптимальную настройку параметров адаптации. Сравнить на контрольной
выборке из последних трех наблюдений точность предсказания по этим мо-
делям . Осуществить прогнозные расчеты (
3
=
τ
), используя более точную
модель.
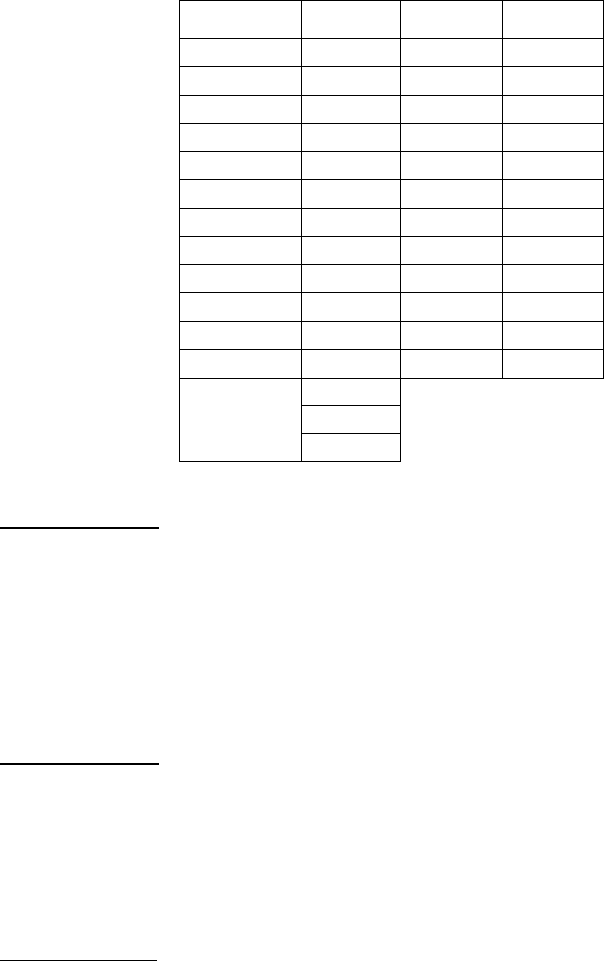
Таблица 7.2.6
Период
y
[
]
1
t
S
[
]
2
t
S
1
197200
144986,4
149027,8
2
154900
147464,8
148637,1
3
157500
149973,6
148971,2
4
109000
139730,2
146660,9
5
90500
127422,6
141851,4
6
62100
111092
134161,5
7
109600
110719
128300,9
8
106600
109689,2
123648
9
163200
123066,9
123502,7
10
172000
135300,2
126452,1
11
267200
168275,1
136907,9
12
260286
191277,8
150500,3
259240
272833
Прогноз
286425
Задание 7.3.3. По данным табл . 7.3.1 для автомобилей Nissan построить
прогнозную модель Хольта с адаптивным механизмом Брауна и сравнить ее
по точности предсказания на контрольной выборке из пяти последних наблю-
дений с моделью в виде адаптивного полинома Брауна первого порядка . Пре -
дусмотреть оптимальную настройку параметров сглаживания. По лучшей мо-
дели осуществить прогноз объема продаж автомобилей этой марки для
5
=
τ
.
Задание 7.3.4. Для автомобилей марок Chrysler и Honda, используя дан-
ные табл . 7.3.1, подобрать наилучшую адаптивную модель (модель Хольта,
модель Хольта с адаптивным механизмом Брауна и адаптивный полином
Брауна первого порядка ) и осуществить прогнозный расчет для
2
=
τ
. Преду-
смотреть оптимальную настройку параметров сглаживания.
Задание 7.3.5. Для автомобилей всех марок, динамика объема продаж ко-
торых представлена в табл . 7.3.1, выбрать наилучшую модель (адаптивный
полином Брауна первого порядка и второго порядка ) с оптимально настроен -
ным параметром экспоненциального сглаживания и осуществить прогнозные
расчеты для
5
=
τ
.

Таблица 7.3.1
Объем продаж новых автомобилей в США
Марки автомобилей
Год
Chrysler Ford Honda Nissan
1988
2208100
3751900
769000642500
1989
2004000
3579900
783100664200
1990
1698100
3317100
854900621600
1991
1507700
2867400
803400583400
1992
1713000
3192500
768800585500
1993
2014800
3562400
717400687700
1994
2204000
3818100
788200774300
1995
2164300
3801000
794600770300
1996
2450800
3843400
843900749800
1997
2303800
3807100
940400728400
1998
2510000
3860200
1009600
624600
8. СИСТЕМЫ РЕГРЕССИОННЫХ УРАВНЕНИЙ
8.1. Расчетные формулы
8.1.1. Необходимое условие идентификации (порядковое условие) фор-
мулируется следующим образом :
если
p
d
=
+
1
, то уравнение идентифицируемо;
если
p
d
<
+
1
, то уравнение неидентифицируемо;
если
p
d
>
+
1
, то уравнение сверхидентифицируемо,
где
d
- число предопределенных переменных отсутствующих в уравнении, но
присутствующих в системе;
p
- число эндогенных переменных в рассматриваемом уравнении.
8.1.2. Достаточное условие идентификации (ранговое условие): ранг мат-
рицы, составленной из коэффициентов при переменных, отсутствующих в
рассматриваемом уравнении, не менее числа эндогенных переменных систе-
мы без единицы.
8.1.3. Оценки коэффициентов внешне не связанной системы регрессион -
ных уравнений:
(
)
=Ω
′
Ω
′
=
−
−
−
yXXXb
1
1
1
ˆ
(
)
(
)
(
)
yIXXIX
m
m
⊗Σ
′
⊗Σ
′
=
−
−
− 1
1
1
,
где
Σ
- ковариационная матрица между случайными составляющими регрес-
сионных моделей, входящих в систему. В практических расчетах заменяется
оценкой
Σ
ˆ
, получаемой для случайных остатков.

8.1.4. Оценки коэффициентов рекурсивной системы регрессионных урав-
нений получаются с помощью МНК.
8.1.5. Процедура построения структурной модели с помощью косвенного
МНК предполагает выполнение следующих трех этапов:
1. Преобразование структурной модели в приведенную форму .
2. Оценивание коэффициентов каждого уравнения приведенной
формы с помощью обычного МНК.
3. Трансформирование полученных коэффициентов приведенной
формы в параметры структурной модели.
8.1.6. Процедура применения двухшагового метода осуществляется в не-
сколько этапов:
1. Преобразование структурной модели в приведенную форму.
2. Оценивание коэффициентов каждого уравнения приведенной
формы с помощью обычного МНК.
3. Если уравнение точно идентифицируемо, то оценки коэффициен -
тов приведенной формы, полученные на втором этапе, принима-
ются за структурные коэффициенты.
Если же уравнение сверхидентифицируемо, то в структурной
форме его эндогенные переменные заменяются расчетными зна-
чениями, полученными из соответствующих уравнений приве-
денной формы, а затем применяется обычный метод наименьших
квадратов.
8.2. Решение типовых задач
Задание 8.2.1. Провести идентификацию ниже приведенной модели и по
данным табл . 8.2.1 построить ее структурную форму:
(
)
+++=
+++=
−
,
,
21322
111
ε
ε
ybybaC
DCbay
где
y
- валовой национальный доход ;
1−
y - валовой национальный доход предшествующего года;
C
- личное потребление;
D
- конечный спрос (помимо личного потребления);
1
ε
и
2
ε
- случайные составляющие.
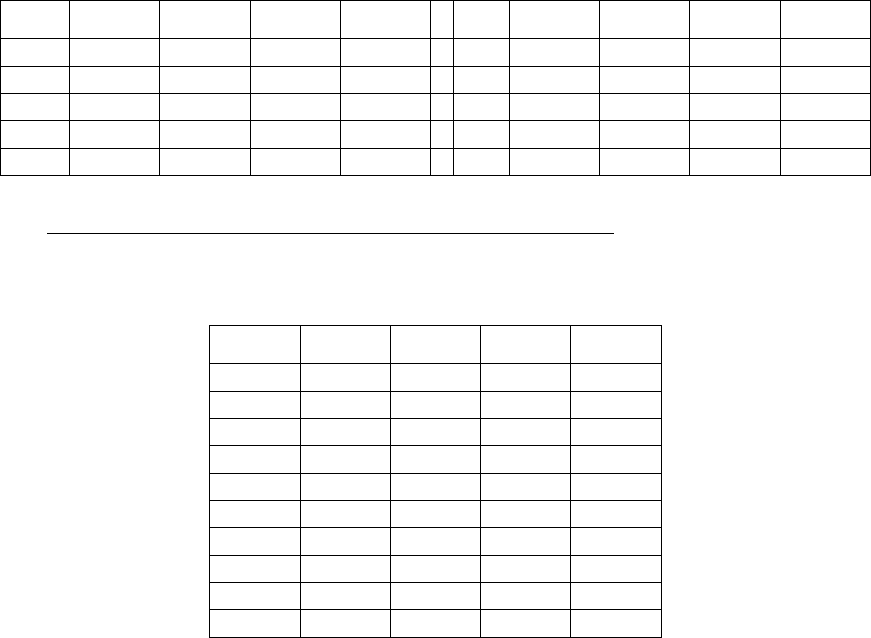
Таблица 8.2.1
Год
D
1−
y
y
C
Год
D
1−
y
y
C
1 -6,8
46,7
3,1
7,4
6 44,7
17,8
37,2
8,6
2 22,4
3,1
22,8
30,4
7 23,1
37,2
35,7
30,0
3 -17,3
22,8
7,8
1,3
8 51,2
35,7
46,6
31,4
4 12,0
7,8
21,4
8,7
9 32,3
46,6
56,0
39,1
5 5,9
21,4
17,8
25,8
Σ
167,5
239,1
248,4
182,7
Решение с помощью табличного процессора Excel.
1. Ввод исходных данных и оформление их в виде удобной для расчетов
табл . 8.2.2.
Таблица 8.2.2
Год
D
1−
y
y
C
1 -6,8
46,7
3,1
7,4
2 22,4
3,1
22,8
30,4
3 -17,3
22,8
7,8
1,3
4 12,0
7,8
21,4
8,7
5 5,9
21,4
17,8
25,8
6 44,7
17,8
37,2
8,6
7 23,1
37,2
35,7
30,0
8 51,2
35,7
46,6
31,4
9 32,3
46,6
56,0
39,1
Σ
167,5
239,1
248,4
182,7
2. Определение идентифицируемости уравнений модели. В данной моде-
ли две эндогенные переменные
y
и
C
, две экзогенные переменные
1−
y и
D
.
Второе уравнение модели точно идентифировано, так как для него выполня-
ется порядковое условие
p
d
=
+
1
(
1
=
d
,
2
=
p
).
Первое уравнение сверхидентифировано, так как в нем в силу того , что
на параметры при переменных
C
и
D
наложены ограничения (они равны
между собой) и, фактически, переменная
C
не рассматривается как эндоген -
ная, выполняется условие
p
d
>
+
1
(
1
=
d
,
1
=
p
).
Достаточное условие идентификации (ранговое условие) для каждого
уравнение очевидным образом выполняется.
Следовательно, второе уравнение можно построить с помощью МНК, а
первое уравнение – с помощью двухшагового МНК.
3. Расчет коэффициентов уравнений приведенной формы:
1121110 −
+
+
=
ydDddy ,
1222120 −
+
+
=
ydDddC .
с помощью пакета «Анализ данных» Excel и оформление результатов в виде
табл . 8.2.3.
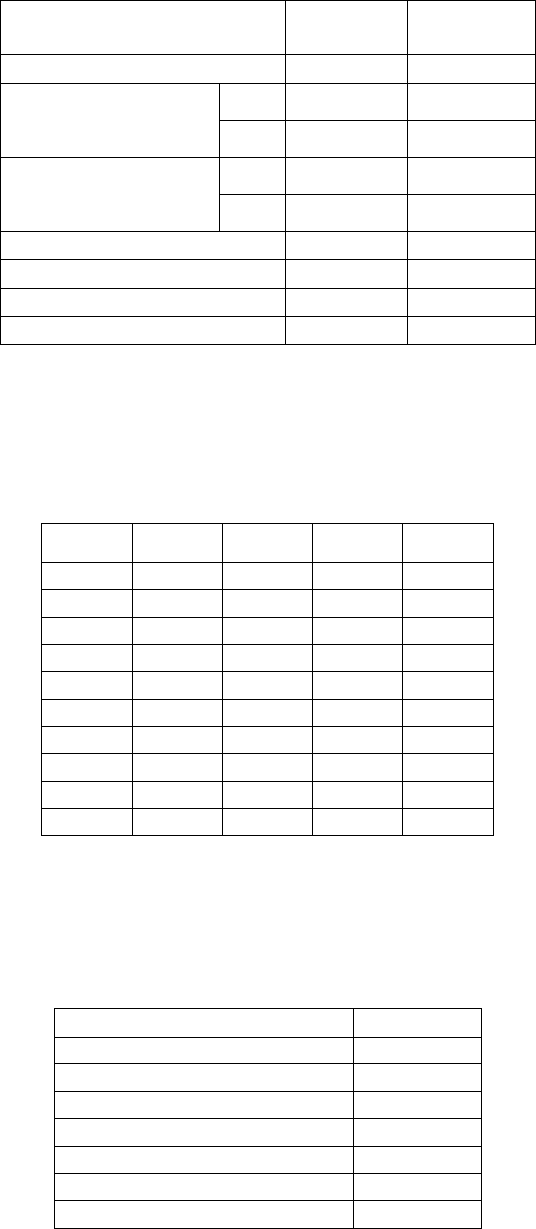
Таблица 8.2.3
Показатели
1-ое урав-
нение
2-ое уравне-
ние
Константа
8,218
8,636
1
d
0,669
0,338
Коэффициенты рег-
рессии
2
d
0,261
0,202
1
s
0,137
0,195
Стандартная ошибка
2
s
0,195
0,277
Множественный R 0,902
0,615
Число наблюдений 9
9
Число степеней свободы 6
6
F - критерий 13,120
1,827
4. Получение расчетных значений эндогенной переменной
C
ˆ
по второму
уравнению построенной приведенной формы и расчет значений
D
C
+
ˆ
.
Оформление результатов в виде табл . 8.2.4.
Таблица 8.2.4
Год
D
C
ˆ
C
D
ˆ
+
y
1 -6,8
15,767
8,967
3,1
2 22,4
16,842
39,242
22,8
3 -17,3
7,386
-9,914
7,8
4 12,0
14,272
26,272
21,4
5 5,9
14,955
20,855
17,8
6 44,7
27,358
72,058
37,2
7 23,1
23,967
47,067
35,7
8 51,2
33,173
84,373
46,6
9 32,3
28,979
61,279
56,0
Σ
167,5
182,7
350,2
248,4
5. Построение первого уравнения структурной формы по данным табл .
8.2.4 с помощью пакета «Анализ данных» и оформление результатов расчета
в виде табл . 8.2.5.
Таблица 8.2.5
Показатели Значения
Константа 7,688
Коэффициент регрессии 0,512
Стандартная ошибка 0,099
Множественный R 0,891
Число наблюдений 9
Число степеней свободы 6
F
- критерий 26,879
Таким образом, первое уравнение структурной формы записывается в виде:
(
)
DCy
+
+
=
51206887 ,, .

6. Получение второго уравнения структурной формы по коэффициентам
приведенной формы.
Определим
D
из первого уравнения приведенной формы:
6690
26102188
1
,
,,
−
−
−
=
yy
D
и подставим его в первое уравнение приведенной формы. Получим:
=
⋅
−++
⋅
−=
− 1
6690
26103380
2020
6690
3380
6690
21883380
6368 yyC
,
,,
,
,
,
,
,,
,
1
070050504844
−
+
+
=
yy ,,,
.
Таким образом, окончательную структурную модель можно записать в виде
(
)
++=
++=
−
.,,,
,,,
1
070050504844
51206887
yyC
DCy
8.3. Контрольные задания
Задание 8.3.1. Применяя необходимое и достаточное условие идентифи-
кации, определите идентифицируемость каждого уравнения записанных ниже
моделей. Определите, какой метод применим для оценки параметров каждой
модели. Запишите приведенную форму этих моделей.
Задание 8.3.1.1. Упрощенная макроэкономическая модель:
функция потребления:
11210 tttt
cyc
ε
α
α
α
+
+
+
=
−
,
функция инвестиций:
(
)
21210 ttttt
eyyri
+
−
+
+
=
−
β
β
β
,
тождество дохода:
tttt
gicy
+
+
=
,
где
t
c- потребление в момент времени t;
t
i
- инвестиции в момент времени t;
t
y - доход в момент времени t;
t
r - процентная ставка в момент времени t;
t
g - государственный расход в момент времени t.
Задание 8.3.1.2. Модель Клейна:
(
)
t
g
t
p
tttt
WWPPC
131210
εαααα +++++=
−
(функция потребления);
ttttt
KPPI
2131210
ε
β
β
β
β
+
+
+
+
=
−−
(функция инвестиций);
tttt
p
t
AXXW
331210
εγγγγ ++++=
−
(функция заработной платы в
частном секторе экономики);
tttt
GICX
+
+
=
(тождество дохода);

p
tttt
WTXP −−= (тождество дохода частного
сектора экономики);
ttt
IKK
+
=
− 1
(тождество запаса капитала),
где
t
C - потребление в момент времени t;
t
I - инвестиции в момент времени t;
p
t
W
- заработная плата частного сектора экономики в момент времени t;
g
t
W - заработная плата государственного сектора экономики в момент
времени t;
t
A - количество лет , прошедших с 1931 года, на момент t;
t
X - доход в момент времени t;
t
P- доход частного сектора экономики в момент времени t;
t
K - запас капитала в момент времени t;
t
T - косвенный налог на предпринимателей плюс чистый экспорт в мо-
мент времени t;
t
G
- государственные расходы, исключая расходы на заработную плату в
момент времени t.
Задание 8.3.1.3. Модель Кейнса :
tttt
YbYbaC
1112111
ε
+
+
+
=
−
(функция потребления);
ttt
YbaI
2212
ε
+
+
=
(функция инвестиций);
tttt
GICY
+
+
=
(тождество дохода),
где
t
C - потребление в момент времени t;
t
I - валовые инвестиции в момент времени t;
t
Y - ВВП в момент времени t;
t
G - государственные расходы в момент времени t.
Задание 8.3.2. Применяя косвенный метод наименьших квадратов, по
данным табл . 8.3.1 построить описывающую потребление модель,
ttt
uYC
+
+
=
β
α
;
ttt
ZCY
+
=
,
где
t
C - потребление в момент времени t;
t
Y - доход в момент времени t;
t
Z - другие расходы (налоги, сбережения и т.п.) в момент времени t.
