Davim J.P. Tribology for Engineers: A Practical Guide
Подождите немного. Документ загружается.

99
Lubrication and roughness
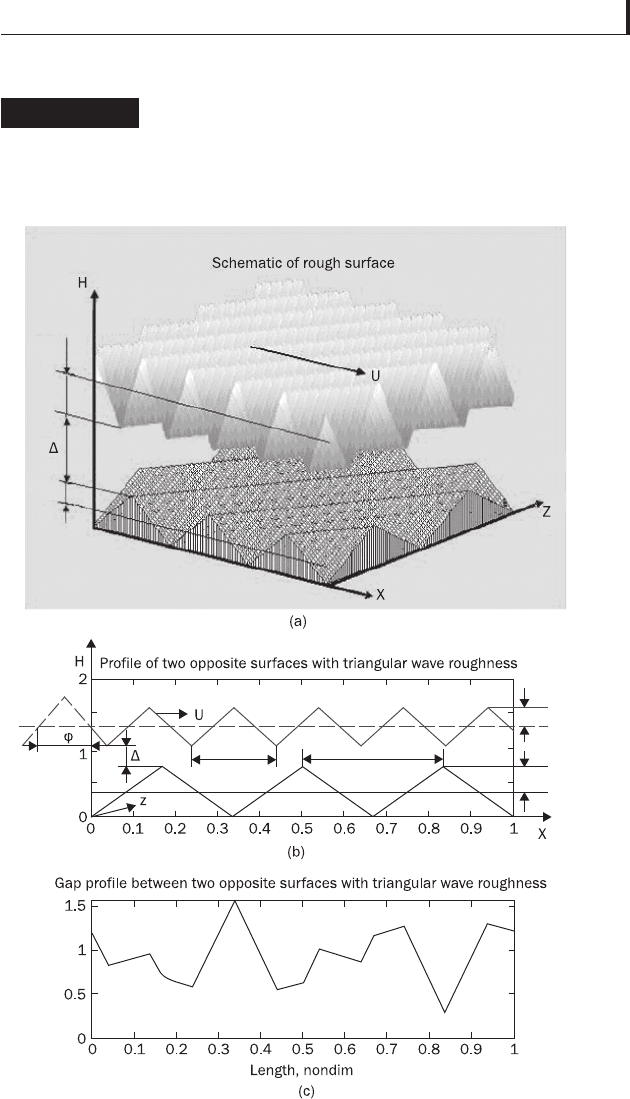
Figure 3.15
Schematic of surface (a), surface profi le (b),
and gap geometry (c) at wave numbers
k
1
x
= 3, k
2
x
= 5, k
1
z
= 2, k
2
z
= 3, and time and
phase displacement of upper surface
Φ = T = 1/(2 k
2x
)
R
a
2
R
a
2
R
a
1
R
a
1
l
2
l
1
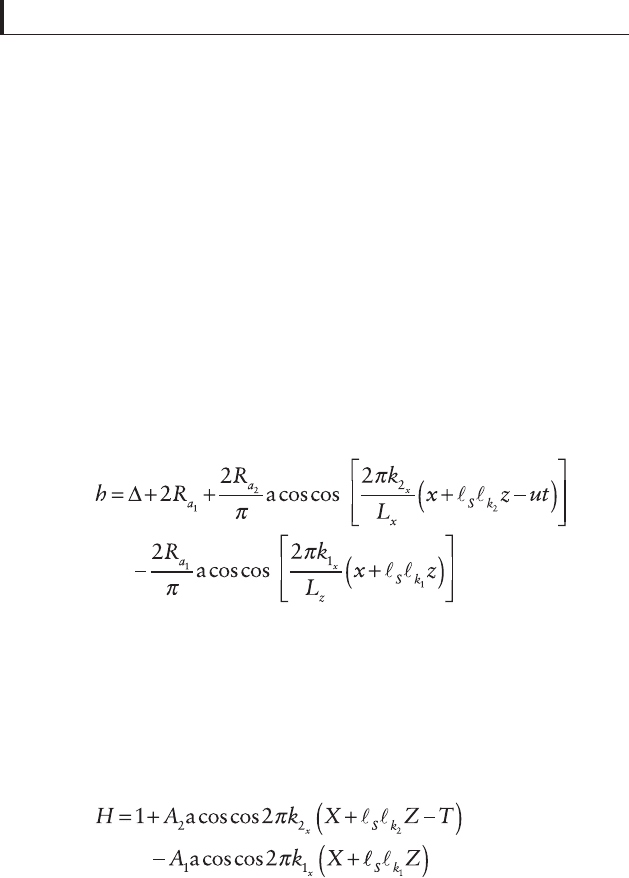
100
Tribology for Engineers
For a pair of surfaces as in Fig. 3.15 with surface profi les
h
(1)
(x,z) and h
(2)
(x,z,t), the fi lm thickness between them is
h(x,z,t) = h
(2)
(x,z,t) − h
(1)
(x,z) [3.43]
In the studied general case we have triangular waves with:
k
1
x
≠ k
2
x
≠ k
1
z
≠ k
2
z
and R
a
1
≠ R
a
2
. Such waves can be described
by a function of the form asin(sin
α
) or acos(cos
β
)/
π
. In the
latter case a pythagorean number is introduced for the
amplitude, varying in the interval 0–1.
Considering all the above and taking the origin of
coordinates at the point where the phase angle
ϕ
1
= 0, the fi lm
thickness [3.43] can be written as
[3.44]
Here for simplicity the initial roughness phase shift ϕ
2
of the
upper surface relative to the lower is given implicitly by the
time t;
k
1
= k
z
1
/k
x
1
and
k
2
= k
z
2
/k
x
2
represent the wave ratios
for the lower and upper surfaces. In dimensionless form
eq. [3.44] reads
[3.45]
where A
1
= R
a
1
/[π (Δ/2 + R
a
1
)], A
2
= R
a
2
/[π (Δ/2 + R
a
1
)], and
X and Y as at [3.26].
For the current case the dimensionless Reynolds’ equation
as per [3.26] with the same boundary conditions as in the
sinusoidal roughness case, should be used.
Next assume
k
1
=
k
2
=
k
, which requires equality of
the wave ratios for the two surfaces,
k
1
Z
/
k
1
X
= k
2
Z
/
k
2
X
, but

101
Lubrication and roughness
admits different wave numbers for them. Thus for
k
1
x
= 2,
k
2
x
= 3,
k
1
z
= 4, and
k
2
z
= 6 we have
k
1
Z
/
k
1
X
=
k
2
Z
/
k
2
X
= 2.
Further, the travelling wave transform is introduced similar
to that in subsection 3.6.1:
[3.46]
Thus for the fi lm thickness
[3.47]
and the 2D Reynolds equation is reduced to 1D
[3.48]
The boundary conditions reduce to P = 0 at
θ
= 0 and
θ
= 1 +
S
k
, and P is identical at
θ
= X and
θ
= X +
S
k
.
The solution of Reynolds’ equation should comply with
these conditions.
Theoretical solution
For further manipulation of eq. [3.31] we need to determine
all X-values at which the waves’ peaks or hollows occur. For
H
1
(
θ
), eq. [3.47], these points correspond to sin 2
π
k
1
x
θ
= 0,
and for H
2
(
θ
) to sin 2
π
k
2
x
(
θ
– T) = 0. Thus for the lower
wave 2
π
k
1
θ
e
=
π
(n
1
–1), and the extreme points are
[3.49]

102
Tribology for Engineers
The second expression in [3.49] should be used in the case of
the X and Z coordinates. Analogously, for the upper wave
, and the extreme points are
[3.50]
where n
1
= 1,2, . . ., 2k
1
x
and n
2
= 1,2, . . ., 2k
2
x
. Thus the gap
contour has m = n
1
+ n
2
break points with coordinates X
e
1
and X
e
2
, and m + 1 segments. Note that eqs. [3.49] and [3.50]
cover both the inner and boundary points.
For solving eq. [3.48] one needs to fi nd the differentials
on its right-hand side and then differentiate it twice.
Differentiating H, we have after some transformations:
with respect to θ
[3.51]
and with respect to T
[3.52]
where
[3.53]
A
= A
1
/A
2
– asperity height ratio, and = k
1
/k
2
– inter-
surface wave ratio.

103
Lubrication and roughness
By eqs. [3.51] and [3.52] the right member of eq. [3.48]
reads
[3.54]
whence
[3.55]
The right member in eq. [3.55] is piecewise constant
along the segments of the gap described by [3.47]. For
simplicity, we replace the variable
θ
in [3.55] by H via the
chain rule
[3.56]
and obtain for each i-th segment the following expression
[3.57]
Accordingly, eq. [3.57] should be integrated over each
segment (a very simple operation) and the resulting integral
normalized against that of its predecessor. After the fi rst
integration
[3.58]
where C
(i)
1
is the integration constant for the segment in
question.

104
Tribology for Engineers
Re-applying the chain rule
[3.59]
After the second integration we have
[3.60]
and fi nally arrive at the equation for the pressure
distribution:
[3.61]
In the case of k
2
= k
1
and A
1
= A
2
, eq. [3.61] has singularities
at points where
δ
A
1
=
δ
A
2
= + 1 ∩ – 1 and is unsuitable,
but still applicable in all cases (at the piecewise segments
of the gap) in which even one of these conditions is not
observed.
The constants of integration have to be determined for
each of the m + 1 segments. This is done via two conditions
– the pressures and pressure gradients should coincide at m
critical (extreme) points reached from the left (i-th segment)
and from the right [(i + 1)-th segment]:
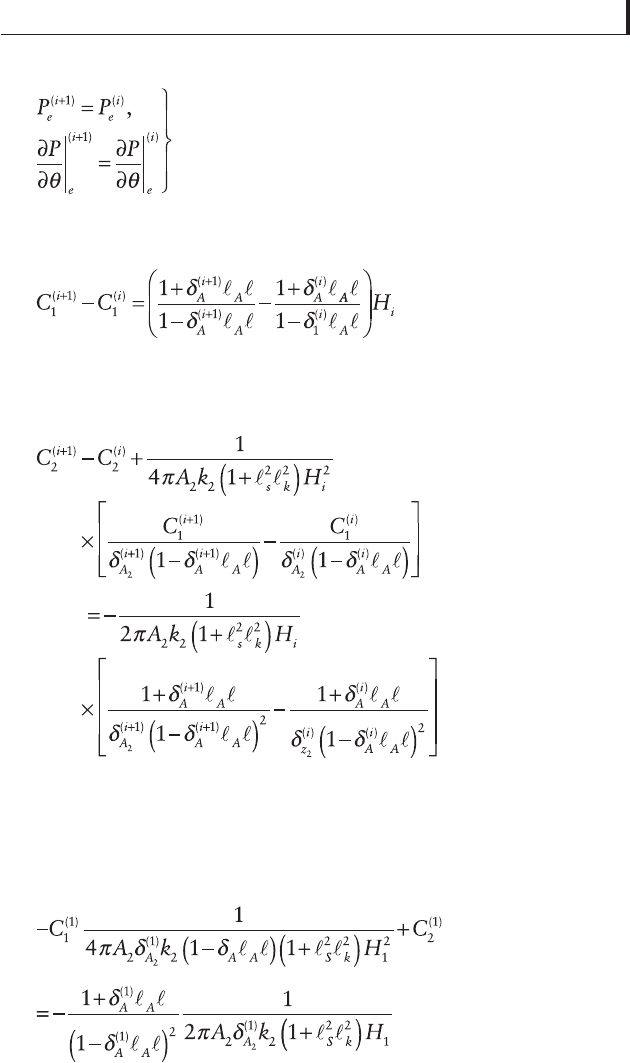
105
Lubrication and roughness
[3.62]
Applying eq. [3.62] to eqs. [3.59] and [3.61], we obtain
[3.63]
and
[3.64]
Thus there are 2m equations and 2(m + 1) constants C
1
and
C
2
. The missing two equations are obtainable from the
boundary conditions:
and

106
Tribology for Engineers
[3.65]
In matrix form, the equations read DC = B where the D is
a square matrix
[3.66]
where
[3.67]
and B is a column vector as follows
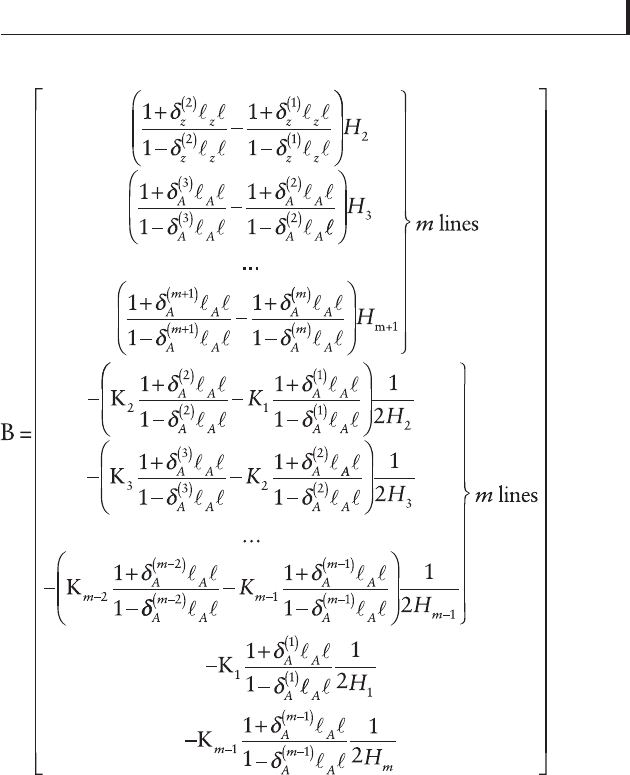
107
Lubrication and roughness
[3.68]
The solution is the column vector of the search constants
C
(i)
1,2
= D\B in which the fi rst m terms are the search constants
C
1
(i)
and the second m terms are C
2
(i)
.
With all constants determined, eq. [3.61] can be
conveniently used for calculating the hydrodynamic pressure
at every point of the lubricating fi lm.
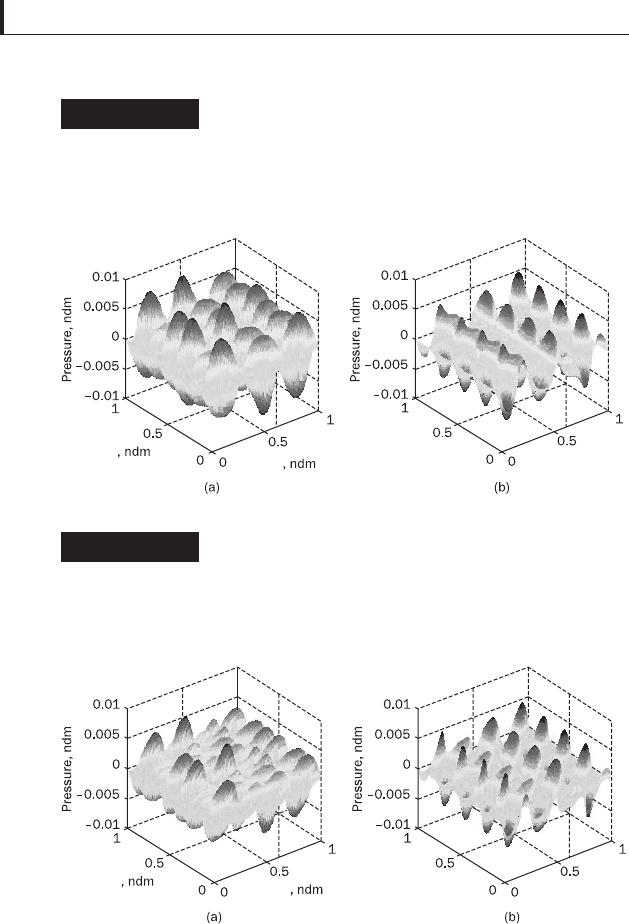
Typical pressure-coordinate and pressure-coordinate-time
distributions at A
1
= A
2
= 0.15 are presented in Fig. 3.16(a)
and (b) (inter-surface wave ratio 3/4) and Fig. 3.17(a) and (b)
(inter-surface wave ratios 3/4 and 4/3). It is seen from
108
Tribology for Engineers
Fig 3.16(a) and Fig. 3.17(a) that the number of maximum/
minimum pressure points in the X-direction is 3 and 4, i.e.
equal to the wave numbers on the stationary surface, and
the same is the case with the Z-direction. The dependence of
pressure on time, Fig 3.16(b) and Fig. 3.17(b), exhibits
Figure 3.17
Typical pressure distribution in lubricating fi lm
between triangular wave surfaces at asperity
height A
1
= A
2
= 0.15, and inner-surface wave
ratio 4/3 along: (a) entire surface profi le at time
1/(k
2
x
) and (b) X, T coordinates at Z = 1/(k
2
x
)
Z
T
X
X
Z
T
X
X
Figure 3.16
Typical pressure distribution in lubricating fi lm
between triangular wave surfaces at asperity
height A
1
= A
2
= 0.15, and inner-surface wave
ratio 3/4, along: (a) entire surface profi le at time
1/(k
2
x
) and (b) X, T coordinates at Z = 1/(k
2
x
)
