Davim J.P. Tribology for Engineers: A Practical Guide

Подождите немного. Документ загружается.

Lubrication and roughness

The integrals in this solution are the same journal-bearing

integrals (Booker, 1965) as in subsection 3.5.2 (cylindrical

journal bearing).

For determining the integration constants we need a

speciﬁ c body geometry and possible real pressure values

assigned at the boundaries. Consider here boundary

conditions as follows

meaning that a divergent region of pressures is assumed, that

the opposite boundaries have the same pressures, and that

the hydrodynamic effect vanishes on the vertical boundaries.

For the lower and upper θ values, we have

[3.35]

which represent a periodic pattern with cycles

–

= 2

k; l

and u denote the lower and upper integration limits

respectively.

Subject to the assigned boundary conditions, C

can be

determined applying the eqs. [3.35] to eq. [3.34], taking

the deﬁ nite integrals between

(X = 0) and

(X = 1),

and assuming p(

) – C

= 0 as in the case of a cylindrical

bearing. Further, substituting this expression and then

determining C

from the boundary condition P = 0 at Z = 0

associated with

, [3.36]

we have an expression for P(

) which, after the requisite

transformations, reads



Tribology for Engineers

[3.37]

In the particular case of equal asperity heights A

= A

= A we

have

, the ﬁ rst coefﬁ cient in

the ﬁ rst term of eq. [3.37] vanishes and the pressure equation

reduces to

[3.38]

Eqs. [3.37] and [3.38] can be reconverted from the variable

θ to the original ones – X, Z and T – by substitution of

expressions [3.30] and [3.36] for

and

; the ﬁ nal expression

is very long and is not given here (available in Burstein,

2010); the P,

, and

expressions constitute a complete

algebraic set of equations which sufﬁ ces for routine arithmetic

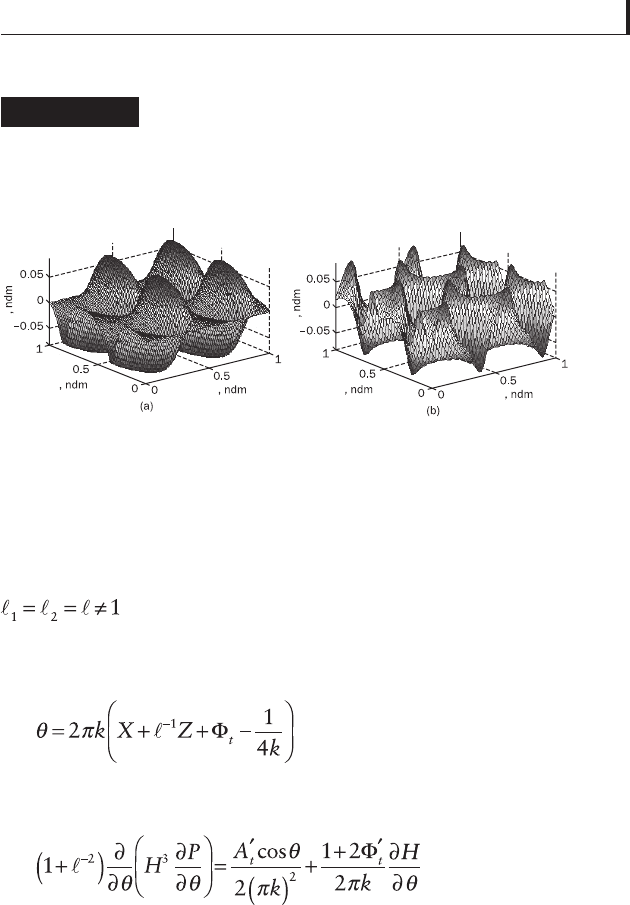
calculations. Typical X, Z – and X, T – pressure distributions

for different roughnesses were calculated with the aid of

these equations and are given in Fig. 3.11(a) and (b). As

the pressure distribution is periodical, its examination for

one wavelength yields complete information about the

surface behaviour as a whole.



Lubrication and roughness

Solution for unequal wave numbers

The above relations can be extended to the case of unequal

wave numbers along axes X and Z, wave number ratios

. In this case the gap equation has the form

[3.28] with A

as per eq. [3.29] and

given by a relation in

which  does not equal 1:

[3.39]

Reynolds’ equation for this case reads

[3.40]

Integrating this equation successively as in the preceding

case, and determining the integration constants from the

same boundary conditions, we easily obtain an analogue of

eq. [3.37] that is valid for the case of different asperity

heights and different wave numbers in the X- and Z-directions

Figure 3.11

Typical pressure distribution in lubricating ﬁ lm

between sinusoidal surfaces with wave

number 2, wave ratio 1, and asperity height of

lower surface 0.5 and upper surface 0.25, at

time 1/(2k) (a) and at coordinate y = 1/(2k) (b).



Tribology for Engineers

[3.41]

with

as per eq. [3.39] and

deﬁ ned by

[3.42]

Eq. [3.41] is more general than eq. [3.37], being valid for

both  = 1 and  ≠ 1.

Typical pressure-coordinate and pressure-coordinate-time

distributions are presented in Fig. 3.12.

It is seen from Fig. 3.12(a), wave ratio 0.5, that the wave

number in the X-direction is 2 and in the Z-direction 4. The

waves along Z = 0 are partly truncated due to displacement

Figure 3.12

Typical pressure distribution in lubricating ﬁ lm

between rough surfaces with wave number 2 at

wave ratio 0.5 with asperity height of lower

surface 0.5 and of upper surface 0.25 along:

(a) entire rough surface at time 1/(2k); (b) X, T

coordinates at Z = 1/(4k)



Lubrication and roughness

of the moving-surface origin by a phase angle 1/(4k). The

time dependence, Fig. 3.12(b), has a more complicated form,

but it should be borne in mind that the plot refers to a single

Z-point and animated pictures are needed for studying the

overall situation. A feature common to the coordinate and

time pressure distributions is asymmetry about the X,Z –

and X,T – planes. This fact and the relevant theoretical

relations were veriﬁ ed by numerical calculations and are

described in the next section.

Effect of asperity height and intra-surface wave

ratio on hydrodynamic pressure

The effect of sinusoidal roughness on the pressure distribution

and normal load support was studied with data presented in

Table 3.1. The rather large reference values of the viscosity

were adopted for a better hydrodynamic effect on the resulting

pressure data.

Parameter Notation Reference value Dimensionality

Sliding velocity u 8.9 m/s

Fluid viscosity

3, 0.3 Pa

Clearance Δ 6

Surface sizes L

, L

10 mm

Asperity height

of lower surface

1.5 . . . 6

Asperity height

of upper surface

Relative gap

= Δ + 2R

Inner-surface

wave ratio



1, 2 dimensionless

Number of proﬁ le

waves

k 100 . . . 35,000 units

Reference values applied in calculations

Table 3.1



Tribology for Engineers

As it is obviously impossible to study all instantaneous

pressures, the maximum value is usually taken for this

purpose. It has a strong inﬂ uence on normal ﬁ lm support

and on such an undesirable effect as cavitation. The latter

occurs when the hydrodynamic pressure reaches, or drops

below, its normal level and is characterized by decomposition

of lube into fractions, bubbling and formation of cavities on

the surface. The adopted reference values of the dynamic

viscosity were those of motor oils SAE 30–50 at 100 °C. The

dimensionles cavitation pressure threshold P

cav

equals

0.91·10

–5

at viscosity 3 Pa·s, and 9.1·10

–3

at 0.3 Pa·s.

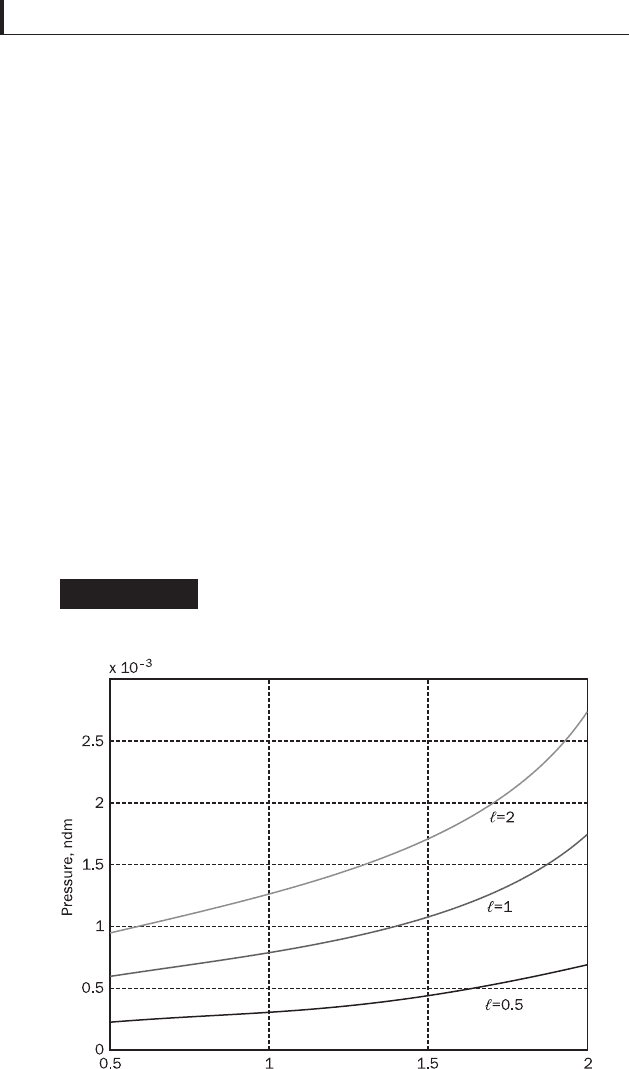
Figure 3.13 shows the dependence of the maximal positive

hydrodynamic pressure for the asperity height ratio range

0.5–2 and for wave ratios 0.5, 1 and 2. Evidently, the pressure

is lower for lower wave ratios; besides, as could be expected,

Figure 3.13

Maximal pressures versus asperity height ratio

at different wave ratios with reference wave

number k

= 100

Asperity height ratio A

, ndm



Lubrication and roughness

if the wave number in the X-direction (that of motion) is

higher than in the Z-direction (wave ratio 0.5), the maximal

pressure is double and more than in the opposite case

(wave ratio 2). As can be seen, the maximal support effect is

reached at larger values of the roughness height ratio A

that is, the roughness of the moving surface affects

the hydrodynamic pressure more strongly than that of the

stationary one. Also, maximal pressures are reached at the

largest values of wave ratio , which means the wave

number in the X-direction outweighs that in the Z-direction.

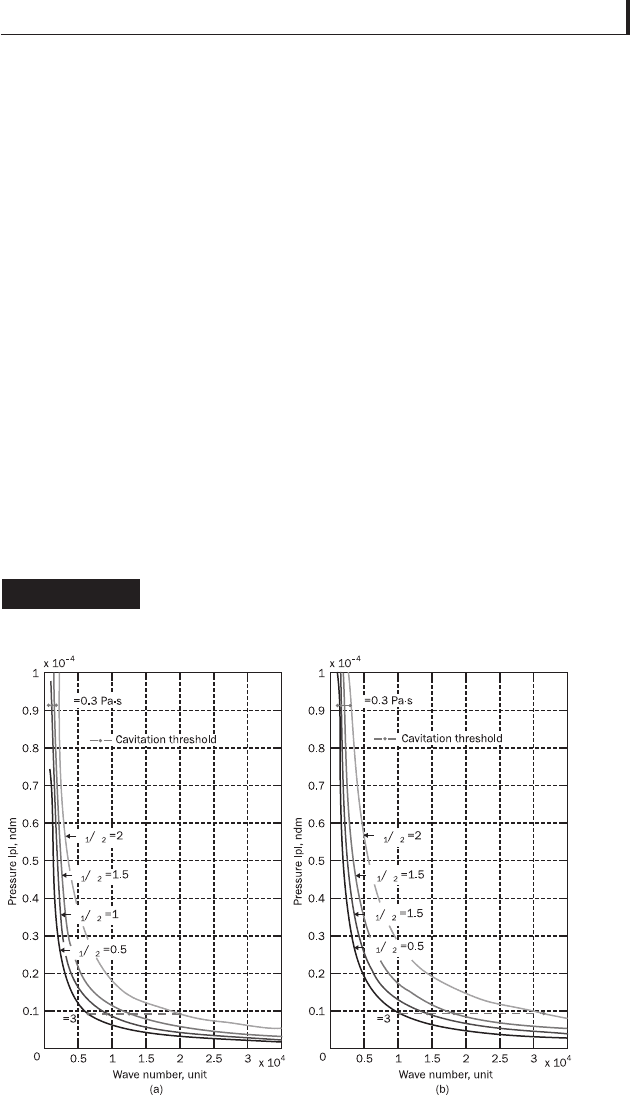
Figure 3.14 shows the dependence of the maximal pressure

on the wave number for asperity height ratio range 0.5–2

at  = 1 and  = 2. Numerical results are also presented in

Table 3.2. As can be expected, higher pressures are reached at

smaller wave numbers. Thus it is preferable to produce surfaces

Figure 3.14

Maximal and cavitation pressures at different

numbers of waves and roughness values at

wave ratio 1 (a) and 2 (b)



Tribology for Engineers

with fewer waves, but unfortunately unrealistic, as in practice

the surfaces of machine parts have thousands of roughness

waves.

The horizontal dotted lines in Fig. 3.14(a) and (b) represent

the two cavitation thresholds for two viscosity values – 3 (lower

threshold line) and 0.3 Pa·s. Below these lines the positive

hydrodynamic effect did not exist at the respective viscosities.

As can be seen, for wave ratio 1 (Fig. 3.14(a)) and viscosity

3 Pa·s the hydrodynamic effect vanished at wave numbers

above 6.5·10

at the lower roughness height ratio 0.5 and

about 19.5·10

at the higher ratio 2. For the lower viscosity

0.3 Pa·s the effect vanished at wave numbers about ten times

lower – from above 0.63·10

and 1.8·10

for the two ratios

respectively. For the unequal wave numbers, in the higher

case (Fig. 14(b) – wave ratio 2), the cavitation threshold was

reached at higher wave numbers, which means that the surface

apparently can contain more waves and survive under this

maximal pressure. The hydrodynamic effect vanished at

higher wave numbers; speciﬁ cally, for viscosity 3 Pa·s it was

above 10.3·10

at asperity height ratio 0.5 and above 31.0·10

at asperity height ratio 2; for viscosity 0.3 Pa·s, cavitation set

in when the surface had about 1.1·10

waves at ratio 0.5 and

3.0·10

waves at asperity ratio 2.

Thus we can say in general that a positive effect takes place

only at wave numbers below 600 at all studied roughness

Cavitation wave number at studied values of

viscosity, wave and asperity height ratios

Table 3.2

Wave

ratio

Viscosity,

Pa·s

= 0.5 A

= 1 A

= 1.5 A

= 2

0.3 628 919 1302 1824

3.0 6545 8571 11754 19534

0.3 1143 1496 1847 3012

3.0 10297 13824 19020 30964



Lubrication and roughness

ratios. As in most real oils the viscosities are ten and more

times lower than the discussed values, and the cavitation

threshold can set in with two-digit or even one-digit numbers

waves. This explains why real mechanical parts do not

exhibit any positive hydrodynamic effect. Most such parts

are sufﬁ ciently large to accommodate tens and hundreds of

thousands of wavelengths, so that a sinusoidal proﬁ le is

irrelevant to them, but for small ones, such as micro- or

nano-scale lubricated surfaces, it can be very effective.

The discussed results were computed by a special program

written in Matlab. The algorithm and other information

about this program are available in Burstein (2009).

Summarizing this analysis, the main results are:

■

The maximal support effect is reached at larger values of

the roughness height ratio A

, indicating that the

roughness of the stationary surface has a stronger effect

on the hydrodynamic pressure than that of the moving

one; this is of practical interest in designing opposite

surfaces with different roughnesses.

■

In the case of equal wave numbers in the X- and Z-directions,

for the higher viscosity 3 Pa·s the hydrodynamic effect

vanishes at a wave number above 6.5·10

at roughness

height ratio 0.5 and at about 19.5·10

at the higher

ratio 2. For the lower viscosity 0.3 Pa·s the hydrodynamic

effect vanishes at wave numbers about ten times lower –

from above 0.63·10

to 1.8·10

for asperity ratios 0.5 and 2

respectively.

■

In the case of unequal wave numbers, the hydrodynamic

effect vanishes for 3Pa·s at above 10.3·10

, roughness ratio

0.5, and at above 31.0·10

, roughness height ratio 2. For 0.3

Pa·s it vanishes when the surface has about 1.1·10

waves at

roughness height ratio 0.5 and 3.0·10

waves at roughness

height ratio 2.



Tribology for Engineers

■

In general, the maximal pressures are reached at larger

wave ratios, indicating that the wave number in the

X-direction outweighs that in the Z-direction.

The results in this section were obtained for the case of equal

wave numbers on the surfaces. The ‘unequal’ case was, until

quite recently, considered intractable because of the serious

difﬁ culties in integrating Reynolds’ equation (see, e.g., Letallear

et al., 2002). This obstacle was removed on introduction of the

triangular roughness pattern.

3.6.3 Hydrodynamic lubrication for

triangular roughness

Take for analysis a control cell – an element on the surfaces

such that integer numbers of waves are located along the

coordinate axes. By this means the behaviour of the whole

surface can be studied on the basis of a small part. Thus a

surface of, say, 10 sq. cm. with asperity width 50 micron

(roughness standard numbers N8–N12) has approximately

630 asperities in each of the X- and Z-directions, but one can

make do with a cell with say 5 asperities only, and apply the

results to all 126 such cells that can be accommodated on the

surface; in parallel, the opposite surface may have a different

asperity width, but again such that the wave numbers in both

directions are integers; in this example, for say 3 waves, the

asperity width must be about 83micron. It is also clear that in

reality the number of asperities in the control cell should be

varied over a relatively narrow range, with the wave numbers

on the two surfaces varying by a factor of 2 or 3.

The X-plane of the proﬁ le geometry and the 3D view for a

control cell with unequal wave numbers and unequal asperity

heights, R

, are shown in Fig. 3.15 for triangular waves, as

an example.

