Даниленко Т.С. Организация и производство геодезических работ при крупном строительстве
Подождите немного. Документ загружается.

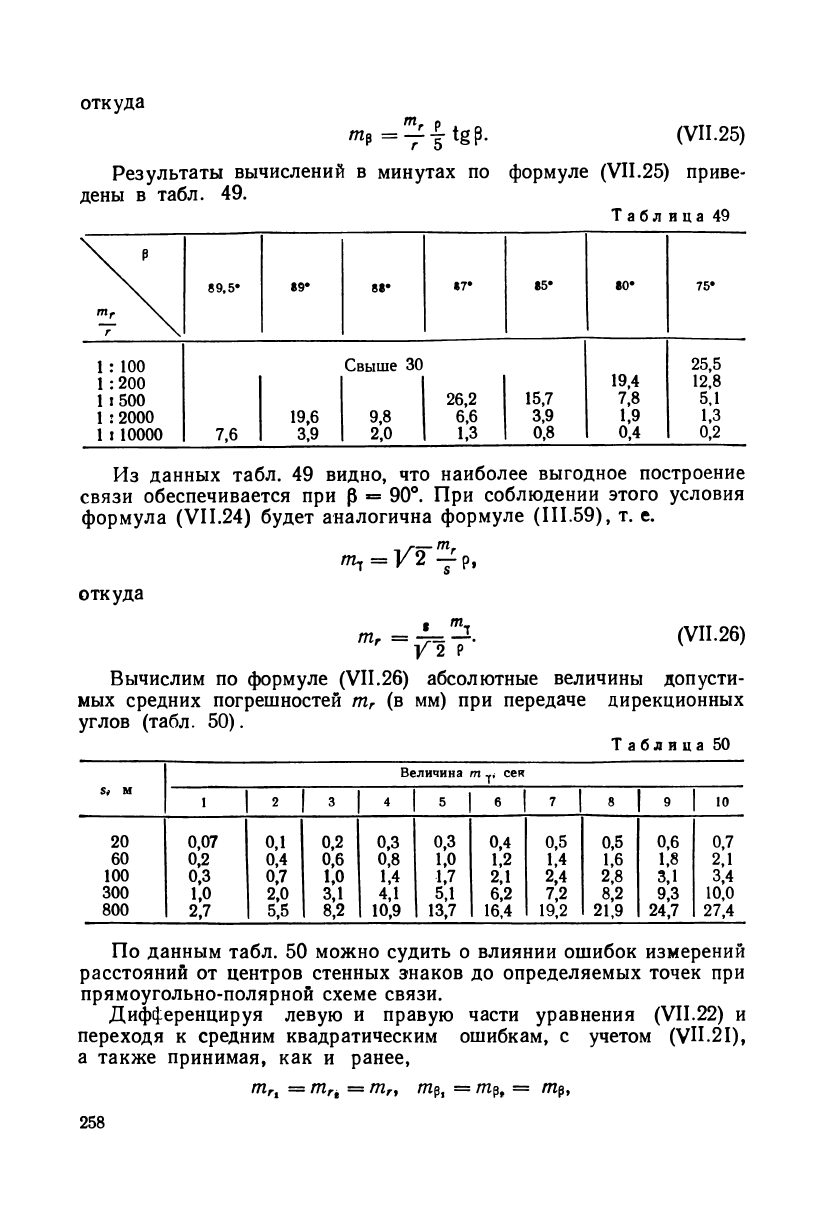
откуда
*вР- (VII.25)
Результаты вычислений в минутах по формуле (VII.25) приве
дены в табл. 49.
Таблица 49
р
m
r
Nv
г V
89.5*
89*
88*
87
е
85*
80*
75
е
1 : 100
Свыше 30
25,5
1 :200
19,4 12,8
1
!
500
26,2
15,7
7,8
5,1
1 :2000
19,6
9,8
6,6
3,9
1,9
1,3
1 ! 10000 7,6
3,9
2,0
1,3
0,8 0,4
0,2
Из данных табл. 49 видно, что наиболее выгодное построение
связи обеспечивается при р = 90°. При соблюдении этого условия
формула (VII.24) будет аналогична формуле (111.59), т. е.
Г
т
г
щ = -f
Р>
откуда
т
г
=4=^1. (VII. 26)
/2Р
Вычислим по формуле (VII.26) абсолютные величины допусти-
мых средних погрешностей т
г
(в мм) при передаче дирекционных
углов (табл. 50).
Таблица 50
Величина i
m у сек
St м
1
2 3
4
5 6
7
8
9 1
1 .0
20
60
100
300
800
0,07
0,2
0,3
1,0
2,7
0,1
0,4
0,7
2,0
5,5
ОО
СлЭ
»—
о о
0,3
0,8
1,4
4,1
10,9
0,3
1,0
1,7
5,1
13,7
0,4
1,2
2,1
6,2
16,4
0,5
1,4
2,4
7,2
19,2
0,5
1,6
2,8
8,2
21,9
0,6
1,8
3,1
9,3
24,7
0,7
2,1
3,4
10,0
27,4
По данным табл. 50 можно судить о влиянии ошибок измерений
расстояний от центров стенных знаков до определяемых точек при
прямоугольно-полярной схеме связи.
Дифференцируя левую и правую части уравнения (VII.22) и
переходя к средним квадратическим ошибкам, с учетом (VII.21),
а также принимая, как и ранее,
т
Г1
= т
Гг
= ш
г
, mp, = tn$
f
= mp,
258

получим
m
2
So
= [(tg т sin Pi — cos pi)
2
+ (tg
T
sin p
2
+ cos p
2
)
2
] m
2
+
m
2
+ [(tgT cos pi + sin p,)
2
r? + (tg
T
cos p
2
- sin p
2
)
2
rl] (VI1.27)
Далее заметим, что при Pi =р
2
=р = 90° и у < у первого
члена правой части формулы (VII.27) коэффициент не превосходит
0,1, а значение т
т
не превышает нескольких миллиметров, поэтому
им можно пренебречь. Тогда
m
m
P i/" 2 ,
r
2
m
So
= — у г\ + г
2
.
(VI 1.28)
Сопоставляя формулы (VII.28) и (II 1.61), замечаем их тож-
дественность. Следовательно, передача от наземных геодезических
знаков на стенные и, наоборот, от центров стенных знаков на на-
земные дирекционного угла и длины линии способом прямоуголь-
но-полярной связи характеризуется примерно одинаковыми по-
грешностями геодезических измерений. В схеме геодезической
связи, представленной на рис. 82, а значения правых частей фор-
мул (VII.26) и (VII.28) уменьшатся в /2 раз. Если принять
г
2
=r\ti, то согласно формуле (VII.28) напишем
m
p
= /
s
° - (VII.29)
р
п!/л
2
+1 «о
v
Придавая различные значения m
So
:s и л, вычислим по форму-
ле (VII.29) величины тр (в минутах) для г, = 1 м и s
0
= 100 м
(табл. 51).
Таблица 51
"Ч
So
Значения п
"Ч
So
, | 2
3 5
10
1 : 1000
242 154
109 68
34
1 : 5000
48
31
22 14
7
1 : 10000
24 15
11
7
3
1 : 20000
12
8
5
3 2
Из табл. 51 следует, что наибольшие допустимые средние ква-
дратические ошибки тр относятся к случаю проектирования дли-
ны линии на направление, параллельное исходному, т. е. при п = 1.
Расчетную формулу оценки влияния центрирования инструмен-
та на измеряемый (задаваемый) угол в схеме прямоугольно-поляр-
ной связи получим из выражения (111.89), подставив значение ко-
эффициента k из табл. 22 (для р = 90°), равное 0,71, так как обыч-
но s : г = п > 7,
=
(VII. 30)
9*
259

здесь е — линейный элемент центрирования теодолита; г — сторона
от вершины измеренного (построенного) угла до стенного знака.
Результаты вычислений по формуле (VII.30) ошибки т
ц
(в ми-
нутах), обусловленные точностью центрирования инструмента и
длиной меньшей стороны угла, приведены в табл. 52.
Таблица 52
0,2 0,5
Величина е, мм
3
10
15
20
0,4
0,2
0,1
0
0
0
0,8
0,4
0,3
0,1
0,1
0
1,6
0,8
0,5
0,3
0,1
о
3,2
1,6
1,0
0,5
0,2
0
4,9
2.4
1.5
0,7
0,4
0
6,5
3,2
2,0
1,0
0,5
0.2
8,1
4.1
2,4
1.2
0,6
0,2
11,4
5.6
3,4
1.7
0,8
0,3
16,2
8,1
4,9
2,4
1,2
0.5
25,4
12,7
7.7
3.8
1.9
0,8
Данные табл. 52 соответствуют и ошибкам за редукцию, так
как при измерении (построении) прямого угла m„ = m
p
, если ли-
нейные элементы центрирования равны, т. е. е = в\. Из данных
табл. 52 можно видеть, что при нитяном отвесе значительно боль-
шее влияние оказывают ошибки центрирования и редукции, чем
ошибки собственно измерения (построения) угла. Данные табл. 49
показывают, что при 90° допустимы довольно большие ошибки
измерения (построения) угла.
Если в створе перпендикуляра оказывается препятствие (столб,
колонна или стержень арматуры), то по формулам (111.67) вычис-
ляют величину q (полагая q = К) допустимого смещения от перпен-
дикуляра, не оказывающего заметного влияния на результат
привязки.
§ 67. ВОССТАНОВЛЕНИЕ И ПЕРЕНЕСЕНИЕ ПУНКТОВ СЕТИ
В производственных условиях нередко появляется необходи-
мость прибегать к построениям различных схем связи существую-
щих и восстанавливаемых или вновь определяемых пунктов.
А. Линейный промер выполняют в закрепленном створе при
отложении заданного отрезка. Небольшой длины отрезки отклады-
вают при помощи стальной компарированной рулетки и соблюдают
правила точного измерения.
Точность положения вновь определяемого пункта относительно
исходного пункта по створу будет характеризоваться суммарной
ошибкой: 1) линейных измерений, 2) нестворенности и 3) фикса-
ции центра.
Ошибку линейных измерений подсчитывают по формуле т
8
=
= Iх У^s. При \х = 0,001 и s = 25 м m
e
= ±5 мм.
260
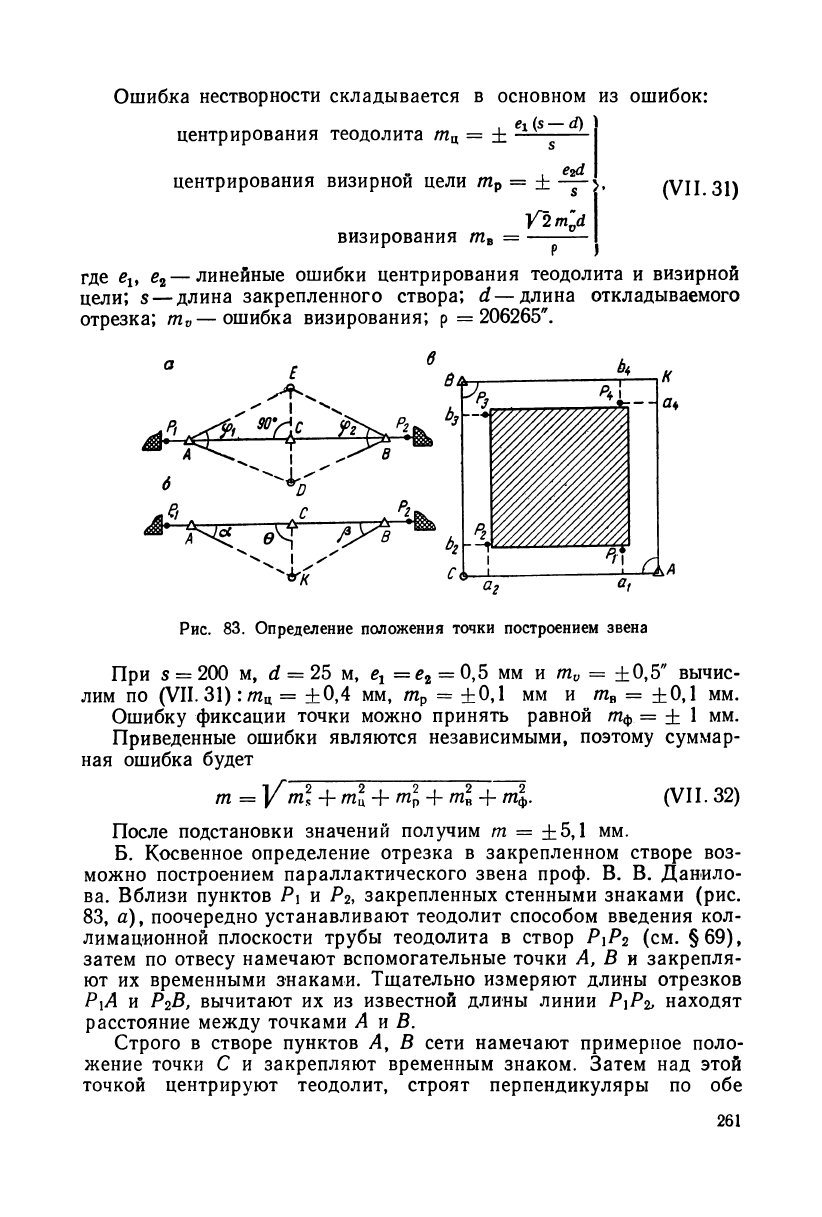
Ошибка нестворности складывается в основном из ошибок:
e
x
(s — d)
центрирования теодолита /тг
ц
= ±
god
центрирования визирнои цели т
р
= ±
——
\
V~2m"
0
d
визирования т„ =
(VII. 31)
где е
ъ
е
2
—линейные ошибки центрирования теодолита и визирной
цели; s — длина закрепленного створа; d — длина откладываемого
отрезка; m
v
—ошибка визирования; р = 206265".
Е
I
Рис. 83. Определение положения точки построением звена
При s = 200 м, d = 25 м, е
г
=е
2
= 0,5 мм и m
v
= ±0,5" вычис-
лим по (VII. 31) :/72
ц
= +0,4 мм, т
р
= +0,1 мм и т
в
= ±0,1 мм.
Ошибку фиксации точки можно принять равной
m<j>
= ± 1 мм.
Приведенные ошибки являются независимыми, поэтому суммар-
ная ошибка будет
т = 1f т\ + ml + ml + ml + т%. (VII. 32)
После подстановки значений получим т = ±5,1 мм.
Б. Косвенное определение отрезка в закрепленном створе воз-
можно построением параллактического звена проф. В. В. Данило-
ва. Вблизи пунктов Pi и Р
2
, закрепленных стенными знаками (рис.
83, а), поочередно устанавливают теодолит способом введения кол-
лимационной плоскости трубы теодолита в створ Р\Р
2
(см. §69),
затем по отвесу намечают вспомогательные точки А, В и закрепля-
ют их временными знаками. Тщательно измеряют длины отрезков
Р\А и Р
2
В, вычитают их из известной длины линии Р\Р% находят
расстояние между точками А и В.
Строго в створе пунктов А, В сети намечают примерное поло-
жение точки С и закрепляют временным знаком. Затем над этой
точкой центрируют теодолит, строят перпендикуляры по обе
261

стороны створа и в точках £>, пересечения с направлениями сто-
рон параллактического угла, заданными в одном из пунктов по-
строением их половин при створе, устанавливают визирные марки.
Длина s звена согласно обозначению на рис. 83, а определяется
по формуле (V. 24). Так как 1
Х
= yctg^-и /
2
=-|-ctgy и заменяя
/
2
= s — /, запишем
|/
lC
t
g
f и 4(
S
-/
l)c
tgf.
Поскольку левые части полученных выражений равны, то, при-
равняв и правые, получим
/, = s
. ¥2
*>5 + tgf
(VII. 33)
Дифференцирование этого выражения и переход к средним квад-
ратическйм ошибкам дает (полагая m
9l
= m
9i
= m
9
)
(VII. 34)
Р
2
Для подсчета необходимой точности измерения параллактичес-
ких углов приравняем правые части формулы, придерживаясь
принципа равных влияний источников ошибок измерений; найдем
х т2 1
Щ =m
s
tg-£-
!
*}/J %
+
{S-h)
2
(VII. 35)
s4
f
Если точка С находится на середине створа А В, то <р
х
=
«р
а
== ср,
/
1 =
/
2
=/ииз (VII. 34)
s
I
mi = — +
2/
2
4
•
4 cos
4
у tg
2
-£-
или, так как 4cos
4
-|-tg
2
y = sin
2
ср,
о о
Р
<Р Р*
Ш/ =
Щ
2 sin
2
р
!
(VII. 36)
Допуская равенство первого и второго членов правой части
формулы (VII. 36), будем иметь
mi = —
V2
т.
т
9
= ^ sin
ср
р = 0,71 sin
ср
у
р
(VII. 37)
262

Следовательно, величина средней квадратической ошибки изме-
рения параллактического угла повышается с увеличением самого
угла.
Так, при
ср
= 10°, m
s
= ±2 см, / = 100 м найдем т
9
= ±4,8",
a mi = ± 14,1 мм.
Если местные условия не позволяют расположить базис звена
перпендикулярно к створу, то применяют звено проф. А. Д. Мотор-
ного.
В створе определяемой линии АВ (рис. 83, б) намечают точку
С, в которой строят перпендикуляр, фиксируя в произвольном
месте точку /С. На пунктах Л, В измеряют углы аир между ство-
рами АВ и направлением на точку К. Длину отрезков вычисляют
по формуле (V.31). Формулу для оценки точности определения
расстояния b получим, если продифференцируем выражение
(V.31), выполним преобразования коэффициентов и перейдем
к средним квадратическим ошибкам, т. е.
«!-№ +Щ&яГ $+- W&h? £
(Vll. 38)
В формуле (VII.38) коэффициенты достаточно вычислять на
логарифмической линейке, если длины линий s, b выразить в сот-
нях метров и сократить р на 10
5
.
При расположении точки С в середине створа а=р, поэтому
коэффициенты второго и третьего членов правой части формулы
(VII.38) одинаковы, a s =2Ь.
Так как I + tg
2
а = 1 + ctg
2
a = ^jjL 2 sin a cos а = sin 2а, то
2 2 2
о mi 2 b
2 т
„ « rni
= -Г + silW if +
62
«8
е в
1Г. (VII. 39)
Если m
s
= ±20 мм, b = 100 м, а = 20°, т
л
= ±5", т
ь
= ±20",
то по формуле (VII. 39) получим т
ь
= ±15,4 мм.
Поставим условие, чтобы и второй и третий члены правой части
формулы (VII. 39) были меньше первого в У2 раз, т. е.
т
с
и j— т
л
-4- = 2 -4s- — = V2b tga -А
2 sin 2a p
r
p
Тогда получим
m
s sin 2a
m
s ctg a ^
/WTT
™'
=
yT = TP'
m
= A ГР' (VII. 40)
Формулы (VII. 40) применимы в расчетах точности измерений
при сгущении строительной разбивочной сети промышленного пред-
приятия.
Так, при m
s
= ±20 мм, b = 200 м, a = 15° по формулам (VII. 40)
найдем: ть = ±ИЛ мм, т
а
= ±2,6", те = ±19".
263

Для контроля и повышения точности определения длин отрез-
ков створа строят двойные параллактические звенья.
На застроенных участках при восстановлении или определении
четвертого пункта применим геодезический четырехугольник без
диагоналей.
На территории строительства промышленного предприятия
пункты, закрепленные стенными реперами, имеют координаты в
системе проектной сетки, принятой на генеральном плане. Это дает
возможность без каких-либо предварительных расчетов выносить
линии, параллельные сторонам разбивочной сети, и способом пря-
моугольно-полярной связи передавать координаты на наземные
знаки А, С, В, (рис. 83, в), выполняя простыё измерения и ариф-
метические действия. В точках А и В задают прямые углы от вы-
несенных створов и в пересечении полученных направлений
фиксируют точку К. Вычисления условных прямоугольных коор-
динат точки К также несложны. Координаты центра стенного зна-
ка определяют способом перпендикуляров и контролируют спосо-
бом полярных координат.
§68. СГУЩЕНИЕ ПУНКТОВ СЕТИ ОТ ЦЕНТРОВ
СТЕННЫХ ЗНАКОВ
Положение отдельных точек и развития съемочного обоснова-
ния в ряде случаев выгодно определять методом триангуляции.
А. Одиночный треугольник. В створе линии Р\Р
2
(рис. 84, а),
закрепленной знаками на сооружениях, или на одинаковом
отстоянии от нее (рис. 84, б) определяют вспомогательные точки
£>i, D
2t
СНОСЯТ на них координаты. Затем эти точки принимают
за исходные, с них определяют точку Z)
3
методом прямой угловой
засечки или наблюдением треугольника.
В первом случае длину исходной стороны получают как раз-
ность известной длины линии Р\Р
2
и измеренных отрезков P\D\ и
P
2
D
2
, во втором — способом прямоугольно-полярной связи, про-
ектированием на параллельный створ, получают D\D
2
= Р\Р
2
.
Длины линий DiDz и D
2
D$ вычисляют по теореме синусов, а
точность их определения оценивают по соответствующей формуле
(IV.47) или (IV.33).
Б. Цепь треугольников. Схемы связи цепи треугольников с
твердыми пунктами могут быть различные.
1. Висячая цепь. Исходную сторону определяют, как и в пре-
дыдущей схеме измерения, и уравнивание результатов наблюде-
ний выполняют по правилам для аналитической сети, а для оцен-
ки точности элементов сети применяют формулы (IV.29) — (IV.31).
2. Цепь треугольников, опирающаяся на твердые стороны.
Цепь между твердыми сторонами АВ и CD (рис. 84, в) большей
частью развивают на окраинах города, на территориях между за-
строенными кварталами и промышленными предприятиями, на
участках строительства гидротехнических сооружений и т. п.
264
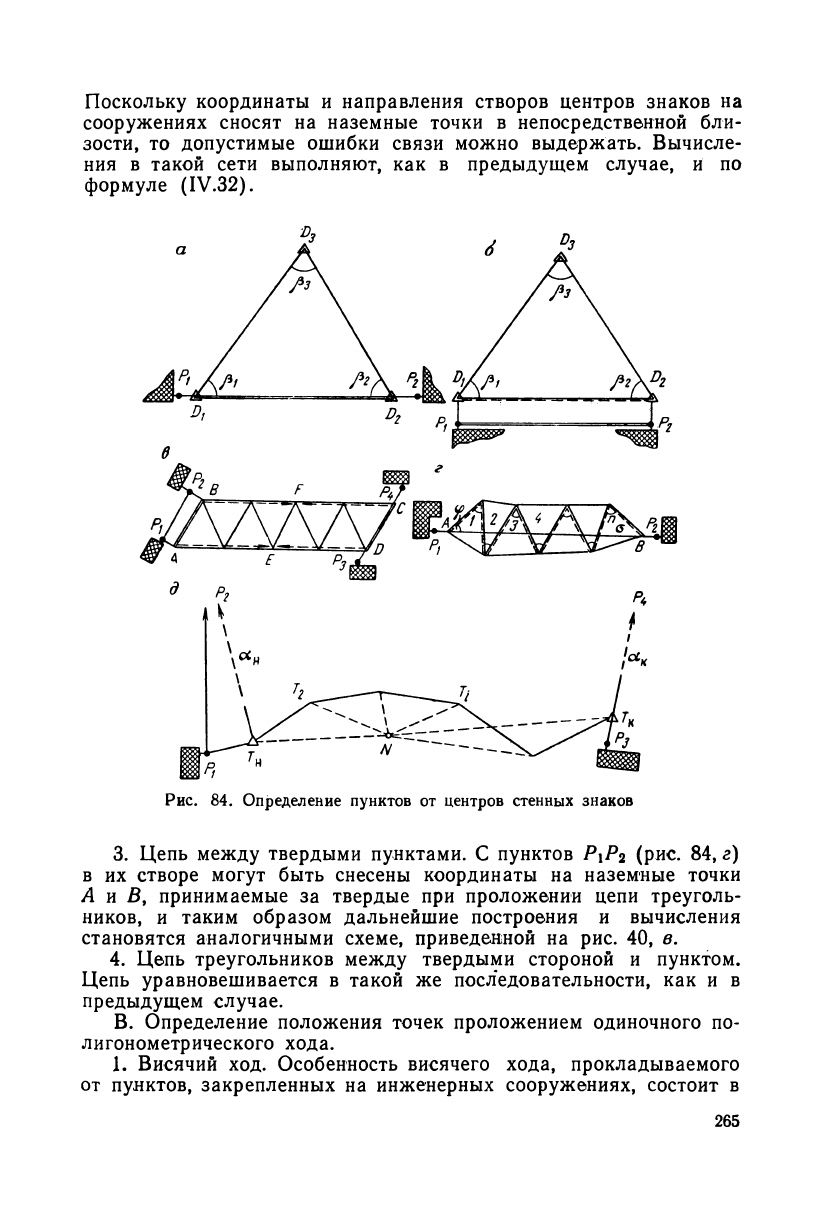
Поскольку координаты и направления створов центров знаков на
сооружениях сносят на наземные точки в непосредственной бли-
зости, то допустимые ошибки связи можно выдержать. Вычисле-
ния в такой сети выполняют, как в предыдущем случае, и по
формуле (IV.32).
Рис. 84. Определение пунктов от центров стенных знаков
3. Цепь между твердыми пунктами. С пунктов Р\Р
2
(рис. 84, г)
в их створе могут быть снесены координаты на наземные точки
Л и В, принимаемые за твердые при проложении цепи треуголь-
ников, и таким образом дальнейшие построения и вычисления
становятся аналогичными схеме, приведенной на рис. 40, в.
4. Цепь треугольников между твердыми стороной и пунктом.
Цепь уравновешивается в такой же последовательности, как и в
предыдущем случае.
В. Определение положения точек проложением одиночного по-
лигонометрического хода.
1. Висячий ход. Особенность висячего хода, прокладываемого
от пунктов, закрепленных на инженерных сооружениях, состоит в
265

определении положения примычного пункта и направления с
него (см. рис. 88).
Оценку точности определения координат и положения точек
хода выполняют по формулам (V.20) и (V.21).
2. Ход полигонометрии, опирающийся на твердые пункты и
дирекционные углы (рис. 84, д). Вначале определяют вспомога-
тельные твердые точки Т
н
, Т
к
и дирекционные углы а
н
, а
к
направ-
лений с них на смежные пункты. Дальнейшие построения соответ-
ствуют обычной схеме (см. рис. 45), а расчетными формулами
оценки точности точек тогда служат (V.22), (V.23) и (V.12),
(V.15).
§ 69. СОВМЕЩЕНИЕ ОСИ ТЕОДОЛИТА С ЗАКРЕПЛЕННЫМ
СТВОРОМ
Под створом понимают вертикальную плоскость, проходящую
на местности через две закрепленные точки.
Установка теодолита в закрепленном створе состоит в совме-
щении оси вращения инструмента с вертикальной плоскостью двух
точек, при этом имеется в виду, что коллимационная плоскость
трубы совпадает с осью вращения инструмента.
В створе между точками А и В (рис. 85, а), закрепленными на
местности, теодолит может быть установлен с очень малым откло-
нением е
с
в точке D. После визирования на точку А и построения
угла, равного 180°*, вследствие неизбежной ошибки визирный
луч может иметь направление DB вместо DB
l
y
отклонившись на
малый угол е. Ошибочно считать, что ось вращения инструмента
совмещена с плоскостью створа.
Обозначим через s
x
и s
2
расстояния от инструмента до точек
Л и В, а через а
х
и а
2
— углы редукции при точках А и В. Со-
гласно чертежу
е^+о,. (VII. 41)
Но е
с
= s
1
tga
1
, е
с
= s
2
tg°2
или
ввиду малого значения углов
е, = у И е
с
= у, поэтому
откуда
<
v
"-«>
Дифференцируя (VII. 42) по переменному г и переходя к сред-
ним квадратическим ошибкам, получим
т
'
с =
(sPFsJ
(
уп
-
43
>
* Поскольку при построении углов 180 и 90° совмещают штрихи алидады
и лимба, что значительно точнее округления при отсчетах, точность построения
углов принимают соответствующей точности измерения угла.
266
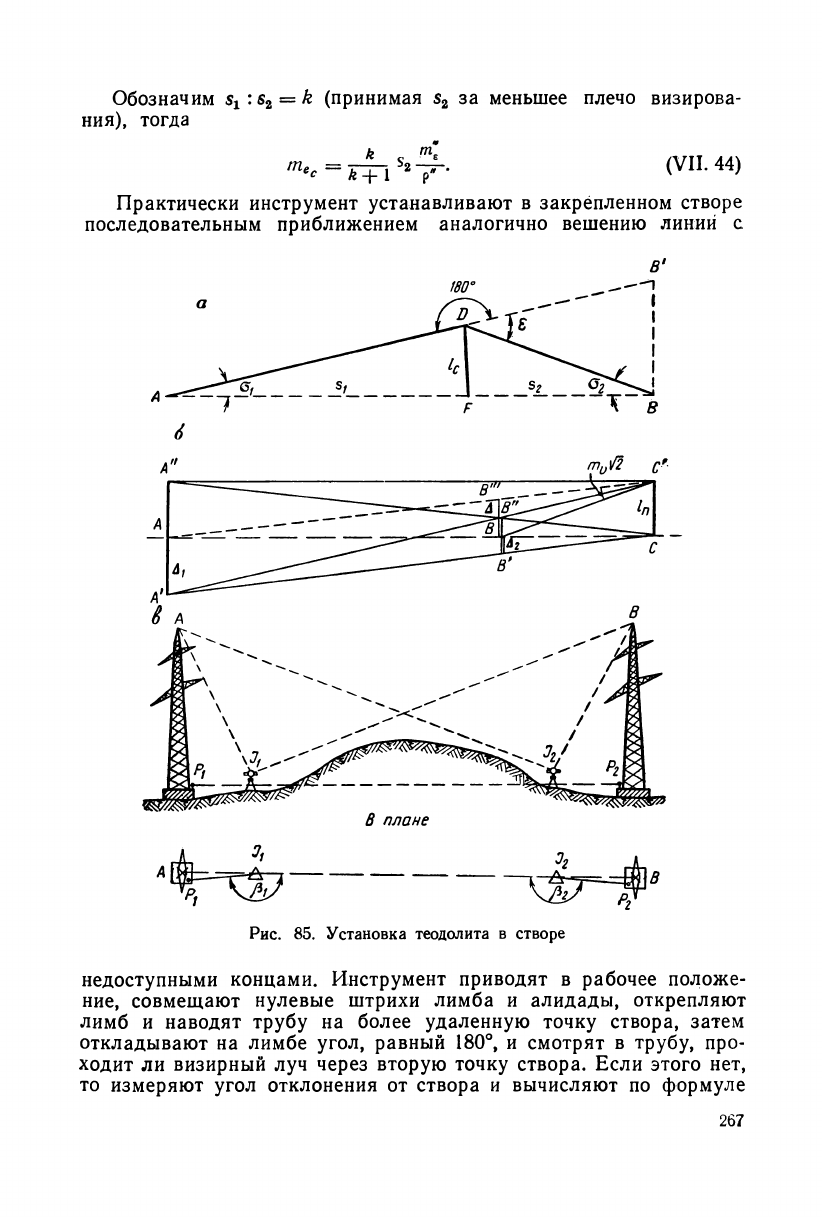
Обозначим s
x
:s
2
= k (принимая s
2
за меньшее плечо визирова-
ния), тогда
Л
Ч
Т- <
VIL44
>
Практически инструмент устанавливают в закрепленном створе
последовательным приближением аналогично вешению линии с
В плане
Рис. 85. Установка теодолита в створе
недоступными концами. Инструмент приводят в рабочее положе-
ние, совмещают нулевые штрихи лимба и алидады, открепляют
лимб и наводят трубу на более удаленную точку створа, затем
откладывают на лимбе угол, равный 180°, и смотрят в трубу, про-
ходит ли визирный луч через вторую точку створа. Если этого нет,
то измеряют угол отклонения от створа и вычисляют по формуле
267
