Daniel W.W. Biostatistics: A Foundation for Analysis in the Health Sciences

Подождите немного. Документ загружается.

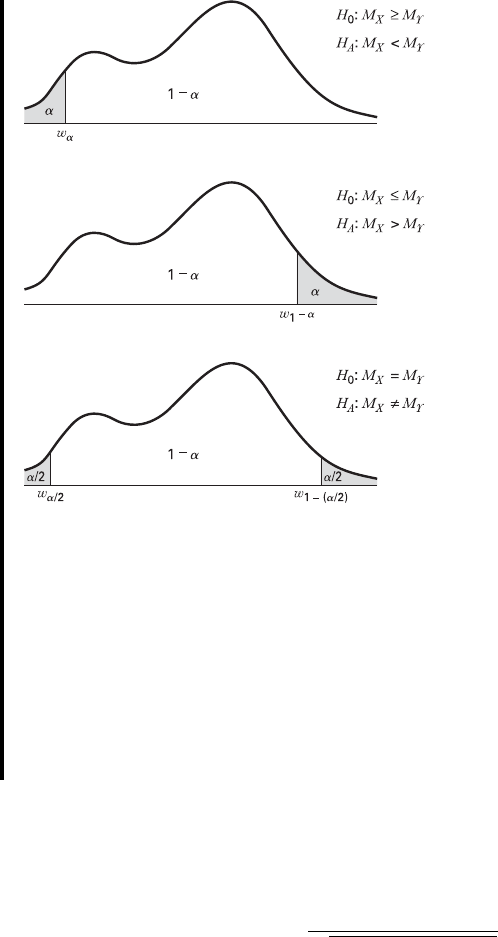
8. Statistical decision. When we enter Table L with and

we ﬁnd the critical value of to be 45. Since we

reject

9. Conclusion. We conclude that is smaller than This leads to the

conclusion that prolonged inhalation of cadmium oxide does reduce the

hemoglobin level.

10. p value. Since we have for this test

■

Large-Sample Approximation When either n or m is greater than 20 we

cannot use Appendix Table L to obtain critical values for the Mann–Whitney test. When

this is the case we may compute

(13.6.2)

and compare the result, for significance, with critical values of the standard normal

distribution.

Mann–Whitney Statistic and the Wilcoxon Statistic As was noted

at the beginning of this section, the Mann–Whitney test is sometimes referred to as the

z =

T - mn>2

1nm1n + m + 12>12

.005 7 p 7 .001.22 6 25 6 30,

25 6 45,w

a = .05,

n = 15, m = 10,

13.6 THE MANN–WHITNEY TEST 707

FIGURE 13.6.1 Mann–Whitney test rejection regions for three sets of hypotheses.

Ranks

y N Mean Rank Sum of Rank

x 1.000000 15 9.67 146.00

2.000000 10 18.00 180.00

Total 25

Test Statistic

Mann-Whitney U 25.000

Wilcoxon W 145.000

Z 2.775

Asymp. Sig. (2-tailed) .006

Exact Sig. [2*(1-tailed Sig.)] .004

a. Not corrected for ties

b. Grouping Variable: y

708 CHAPTER 13 NONPARAMETRIC AND DISTRIBUTION-FREE STATISTICS

Dialog box: Session command:

Stat ➤ Nonparametrics ➤ Mann–Whitney MTB > Mann-Whitney 95.0

C1 C2;

SUBC > Alternative 1.

Type C1 in First Sample and C2 in Second Sample.

At Alternative choose less than.

Click OK .

Output:

Mann–Whitney Test and CI: C1, C2

C1 N  15 Median  15.300

C2 N  10 Median  16.550

Point estimate for ETA1  ETA2 is 1.300

95.1 Percent C.I. for ETA1  ETA2 is (2.300,0.600)

W  145.0

Test of ETA1  ETA2 vs. ETA1  ETA2 is signiﬁcant at 0.0030

The test is signiﬁcant at 0.0030 (adjusted for ties)

FIGURE 13.6.2 MINITAB procedure and output for Example 13.6.1.

FIGURE 13.6.3 SPSS output for Example 13.6.1.

Mann–Whitney-Wilcoxon test. Indeed, many computer packages give the test value of

both the Mann–Whitney test (U) and the Wilcoxon test (W). These two tests are alge-

braically equivalent tests, and are related by the following equality when there are no

ties in the data:

(13.6.3)

Computer Analysis Many statistics software packages will perform the

Mann–Whitney test. With the data of two samples stored in Columns 1 and 2, for

example, MINITAB will perform a one-sided or two-sided test. The MINITAB proce-

dure and output for Example 13.6.1 are shown in Figure 13.6.2.

The SPSS output for Example 13.6.1 is shown in Figure 13.6.3. As we see this out-

put provides the Mann–Whitney test, the Wilcoxon test, and large-sample z approximation.

EXERCISES

13.6.1 Cranor and Christensen (A-4) studied diabetics insured by two employers. Group 1 subjects

were employed by the City of Asheville, North Carolina, and group 2 subjects were employed

by Mission–St. Joseph’s Health System. At the start of the study, the researchers performed the

Mann–Whitney test to determine if a significant difference in weight existed between the two

study groups. The data are displayed in the following table.

Weight (Pounds)

Group 1 Group 2

252 215 240 185 195 220

240 190 302 310 210 295

205 270 312 212 190 202

200 159 126 238 172 268

170 204 268 184 190 220

170 215 215 136 140 311

320 254 183 200 280 164

148 164 287 270 264 206

214 288 210 200 270 170

270 138 225 212 210 190

265 240 258 182 192

203 217 221 225 126

Source: Carole W. Carnor, Ph.D. Used with permission.

May we conclude, on the basis of these data, that patients in the two groups differ signiﬁcantly

with respect to weight? Let

13.6.2 One of the purposes of a study by Liu et al. (A-5) was to determine the effects of MRZ 2/579 (a

receptor antagonist shown to provide neuroprotective activity in vivo and in vitro) on neurological

a = .05.

U + W =

m1m + 2n + 12

EXERCISES 709

deﬁcit in Sprague–Dawley rats. In the study, 10 rats were to receive MRZ 2/579 and nine rats were

to receive regular saline. Prior to treatment, researchers studied the blood gas levels in the two groups

of rats. The following table shows the levels for the two groups.

Saline (mmHg) MRZ 2/579 (mmHg)

112.5 133.3

106.3 106.4

99.5 113.1

98.3 117.2

103.4 126.4

109.4 98.1

108.9 113.4

107.4 116.8

116.5

Source: Ludmila Belayev, M.D. Used with permission.

May we conclude, on the basis of these data, that, in general, subjects on saline have, on average,

lower levels at baseline? Let

13.6.3 The purpose of a study by researchers at the Cleveland (Ohio) Clinic (A-6) was to determine if

the use of Flomax

reduced the urinary side effects commonly experienced by patients following

brachytherapy (permanent radioactive seed implant) treatment for prostate cancer. The following

table shows the American Urological Association (AUA) symptom index scores for two groups of

subjects after 8 weeks of treatment. The higher the AUA index, the more severe the urinary obstruc-

tion and irritation.

AUA Index (Flomax

) AUA Index (Placebo)

1511 1612

2611 2613

2611 2614

2712 2617

2712 3718

3713 3819

3714 3820

3816 3923

4816 4923

4818 410

4821 410

4931 511

49 511

410 512

Source: Chandana Reddy, M.S. Used with permission.

May we conclude, on the basis of these data, that the median AUA index in the Flomax

group

differs signiﬁcantly from the median AUA index of the placebo group? Let a = .05.

a = .01.pO

710 CHAPTER 13 NONPARAMETRIC AND DISTRIBUTION-FREE STATISTICS

13.7 THE KOLMOGOROV–SMIRNOV

GOODNESS-OF-FIT TEST

When one wishes to know how well the distribution of sample data conforms to some

theoretical distribution, a test known as the Kolmogorov–Smirnov goodness-of-ﬁt test

provides an alternative to the chi-square goodness-of-ﬁt test discussed in Chapter 12. The

test gets its name from A. Kolmogorov and N. V. Smirnov, two Russian mathematicians

who introduced two closely related tests in the 1930s.

Kolmogorov’s work (6) is concerned with the one-sample case as discussed here.

Smirnov’s work (7) deals with the case involving two samples in which interest centers

on testing the hypothesis that the distributions of the two-parent populations are iden-

tical. The test for the ﬁrst situation is frequently referred to as the Kolmogorov–Smirnov

one-sample test. The test for the two-sample case, commonly referred to as the

Kolmogorov–Smirnov two-sample test, will not be discussed here.

The Test Statistic In using the Kolmogorov–Smirnov goodness-of-fit test, a

comparison is made between some theoretical cumulative distribution function,

and a sample cumulative distribution function, The sample is a random sample

from a population with unknown cumulative distribution function It will be recalled

(Section 4.2) that a cumulative distribution function gives the probability that X is equal

to or less than a particular value, x. That is, by means of the sample cumulative distri-

bution function, we may estimate If there is close agreement between

the theoretical and sample cumulative distributions, the hypothesis that the sample was

drawn from the population with the speciﬁed cumulative distribution function, is

supported. If, however, there is a discrepancy between the theoretical and observed cumu-

lative distribution functions too great to be attributed to chance alone, when is true,

the hypothesis is rejected.

The difference between the theoretical cumulative distribution function, and

the sample cumulative distribution function, is measured by the statistic D, which

is the greatest vertical distance between and When a two-sided test is appro-

priate, that is, when the hypotheses are

for all x from

for at least one x

the test statistic is

(13.7.1)

which is read, “D equals the supremum (greatest), over all x, of the absolute value of the

difference minus ”

The null hypothesis is rejected at the level of significance if the computed

value of D exceeds the value shown in Appendix Table M for (two-sided) and

the sample size n.

1 - a

1X 2.F

1X 2

D = sup

1x2- F

1x2

: F1x2Z F

1x2

to +

: F1x2= F

1x2

1x2.F

1x2

1x2,

P1X … x2.F

1x2,

F1x2.

1x2.

1x2,

13.7 THE KOLMOGOROV–SMIRNOV GOODNESS-OF-FIT TEST 711

Assumptions The assumptions underlying the Kolmogorov–Smirnov test include

the following:

1. The sample is a random sample.

2. The hypothesized distribution is continuous.

When values of D are based on a discrete theoretical distribution, the test is con-

servative. When the test is used with discrete data, then, the investigator should bear in

mind that the true probability of committing a type I error is at most equal to the

stated level of signiﬁcance. The test is also conservative if one or more parameters have

to be estimated from sample data.

EXAMPLE 13.7.1

Fasting blood glucose determinations made on 36 nonobese, apparently healthy, adult males

are shown in Table 13.7.1. We wish to know if we may conclude that these data are not

from a normally distributed population with a mean of 80 and a standard deviation of 6.

Solution:

1. Data. See Table 13.7.1.

2. Assumptions. The sample available is a simple random sample from a

continuous population distribution.

3. Hypotheses. The appropriate hypotheses are

for all x from to

for at least one x

Let

4. Test statistic. See Equation 13.7.1.

5. Distribution of test statistic. Critical values of the test statistic for

selected values of are given in Appendix Table M.

6. Decision rule. Reject if the computed value of D exceeds .221, the

critical value of D for and

7. Calculation of test statistic. Our first step is to compute values of

as shown in Table 13.7.2.F

1x2

a = .05.n = 36

a = .05.

: F1x2Z F

1x2

: F1x2= F

1x2

712

CHAPTER 13 NONPARAMETRIC AND DISTRIBUTION-FREE STATISTICS

TABLE 13.7.1 Fasting Blood Glucose Values

(mg/100 ml) for 36 Nonobese, Apparently

Healthy, Adult Males

75 92 80 80 84 72

84 77 81 77 75 81

80 92 72 77 78 76

77 86 77 92 80 78

68 78 92 68 80 81

87 76 80 87 77 86

Each value of is obtained by dividing the corresponding

cumulative frequency by the sample size. For example, the ﬁrst value of

We obtain values of by ﬁrst converting each observed value

of x to a value of the standard normal variable, z. From Appendix Table

D we then ﬁnd the area between and z. From these areas we are

able to compute values of The procedure, which is similar to that

used to obtain expected relative frequencies in the chi-square goodness-

of-ﬁt test, is summarized in Table 13.7.3.

1x2.

1x2

1x2= 2>36 = .0556.

1x2

13.7 THE KOLMOGOROV–SMIRNOV GOODNESS-OF-FIT TEST 713

TABLE 13.7.2 Values of for Example 13.7.1

Cumulative

Frequency Frequency

68 2 2 .0556

72 2 4 .1111

75 2 6 .1667

76 2 8 .2222

77 6 14 .3889

78 3 17 .4722

80 6 23 .6389

81 3 26 .7222

84 2 28 .7778

86 2 30 .8333

87 2 32 .8889

92 4 36 1.0000

(x )

TABLE 13.7.3 Steps in Calculation

of for Example 13.7.1

68 .0228

72 .0918

75 .2033

76 .2514

77 .3085

78 .3707

80 .00 .5000

81 .17 .5675

84 .67 .7486

86 1.00 .8413

87 1.17 .8790

92 2.00 .9772

-.33

-.50

-.67

-.83

-1.33

-2.00

(x)z  (x  80)

(x)

The test statistic D may be computed algebraically, or it may be

determined graphically by actually measuring the largest vertical distance

between the curves of and on a graph. The graphs of the

two distributions are shown in Figure 13.7.1.

Examination of the graphs of and reveals that

Now let us compute the value of D alge-

braically. The possible values of are shown in Table

13.7.4. This table shows that the exact value of D is .1547.

8. Statistical decision. Reference to Table M reveals that a computed D

of .1547 is not signiﬁcant at any reasonable level. Therefore, we are not

willing to reject .

9. Conclusion. The sample may have come from the speciﬁed distribution.

10. p value. Since we have a two-sided test, and since . we

have .p 7 .20

1547 6 .174,

1x2- F

1x2

D L .16 = 1.72 - .562.

1x2F

1x2

1x2F

1x2

714

CHAPTER 13 NONPARAMETRIC AND DISTRIBUTION-FREE STATISTICS

68 70 72 74 76 78 80 82 84 86 88 90 92 94

Cumulative relative frequency

1.00

.90

.80

.70

.60

.50

.40

.30

.20

.10

FIGURE 13.7.1 and for Example 13.7.1.F

1x2F

1x2

TABLE 13.7.4 Calculation of for

Example 13.7.1

68 .0556 .0228 .0328

72 .1111 .0918 .0193

75 .1667 .2033 .0366

76 .2222 .2514 .0292

77 .3889 .3085 .0804

78 .4722 .3707 .1015

80 .6389 .5000 .1389

81 .7222 .5675 .1547

84 .7778 .7486 .0292

86 .8333 .8413 .0080

87 .8889 .8790 .0099

92 1.0000 .9772 .0228

(x)  F

(x)

(x)F

(x)

円F

(x)  F

(x)円

■

StatXact is often used for nonparametric statistical analysis. This particular soft-

ware program has a nonparametric module that contains nearly all of the commonly

used nonparametric tests, and many less common, but useful, procedures as well. Com-

puter analysis using StatXact for the data in Example 13.7.1 is shown in Figure 13.7.2.

Note that it provides the test statistic of D  0.156 and the exact two-sided p value

of .3447.

A Precaution The reader should be aware that in determining the value of D, it

is not always sufficient to compute and choose from the possible values of

The largest vertical distance between and may not occur

at an observed value, x, but at some other value of X. Such a situation is illustrated in

Figure 13.7.3. We see that if only values of at the left endpoints of

the horizontal bars are considered, we would incorrectly compute D as

One can see by examining the graph, however, that the largest vertical distance between

and occurs at the right endpoint of the horizontal bar originating at the

point corresponding to and the correct value of D is

One can determine the correct value of D algebraically by computing, in addition

to the differences the differences for all values of

where the number of different values of x and

The correct value of the test statistic will then be

(13.7.2)D = maximum

1 … i … r

5maximum3

2- F

i -1

2- F

2= 0.r =i = 1, 2,...,r + 1,

i -1

2- F

ƒƒ

1x2- F

1x2

.5 - .2

= .3.x = .4,

1x2F

1x2

.2 - .4

= .2.

1x2- F

1x2

1x2F

1x2

1x2- F

1x2

13.7 THE KOLMOGOROV–SMIRNOV GOODNESS-OF-FIT TEST 715

FIGURE 13.7.2 StatXact output for Example 13.7.1

Advantages and Disadvantages The following are some important

points of comparison between the Kolmogorov–Smirnov and the chi-square goodness-

of-fit tests.

1. The Kolmogorov–Smirnov test does not require that the observations be grouped as

is the case with the chi-square test. The consequence of this difference is that the

Kolmogorov–Smirnov test makes use of all the information present in a set of data.

2. The Kolmogorov–Smirnov test can be used with any size sample. It will be recalled

that certain minimum sample sizes are required for the use of the chi-square test.

3. As has been noted, the Kolmogorov–Smirnov test is not applicable when parame-

ters have to be estimated from the sample. The chi-square test may be used in these

situations by reducing the degrees of freedom by 1 for each parameter estimated.

4. The problem of the assumption of a continuous theoretical distribution has already

been mentioned.

EXERCISES

13.7.1 The weights at autopsy of the brains of 25 adults suffering from a certain disease were as follows:

Weight of Brain (grams)

859 1073 1041 1166 1117

962 1051 1064 1141 1202

973 1001 1016 1168 1255

904 1012 1002 1146 1233

920 1039 1086 1140 1348

716 CHAPTER 13 NONPARAMETRIC AND DISTRIBUTION-FREE STATISTICS

.2 .4 .5 .8 1.0

Cumulative relative frequency

1.0

FIGURE 13.7.3 Graph of ﬁctitious data showing correct calculation of