Daniel W.W. Biostatistics: A Foundation for Analysis in the Health Sciences

Подождите немного. Документ загружается.

Assumptions The assumptions underlying multiple regression analysis are as

follows.

1. The are nonrandom (ﬁxed) variables. This assumption distinguishes the multi-

ple regression model from the multiple correlation model, which will be presented

in Section 10.6. This condition indicates that any inferences that are drawn from

sample data apply only to the set of X values observed and not to some larger col-

lection of X’s. Under the regression model, correlation analysis is not meaningful.

Under the correlation model to be presented later, the regression techniques that

follow may be applied.

2. For each set of values there is a subpopulation of Y values. To construct certain

conﬁdence intervals and test hypotheses, it must be known, or the researcher must

be willing to assume, that these subpopulations of Y values are normally distributed.

Since we will want to demonstrate these inferential procedures, the assumption of

normality will be made in the examples and exercises in this chapter.

3. The variances of the subpopulations of Y are all equal.

4. The Y values are independent. That is, the values of Y selected for one set of X

values do not depend on the values of Y selected at another set of X values.

The Model Equation The assumptions for multiple regression analysis may be

stated in more compact fashion as

(10.2.1)

where is a typical value from one of the subpopulations of Y values; the are called

the regression coefﬁcients; are, respectively, particular values of the inde-

pendent variables and is a random variable with mean 0 and variance

the common variance of the subpopulations of Y values. To construct conﬁdence

intervals for and test hypotheses about the regression coefﬁcients, we assume that the

are normally and independently distributed. The statements regarding are a conse-

quence of the assumptions regarding the distributions of Y values. We will refer to Equa-

tion 10.2.1 as the multiple linear regression model.

When Equation 10.2.1 consists of one dependent variable and two independent

variables, that is, when the model is written

(10.2.2)

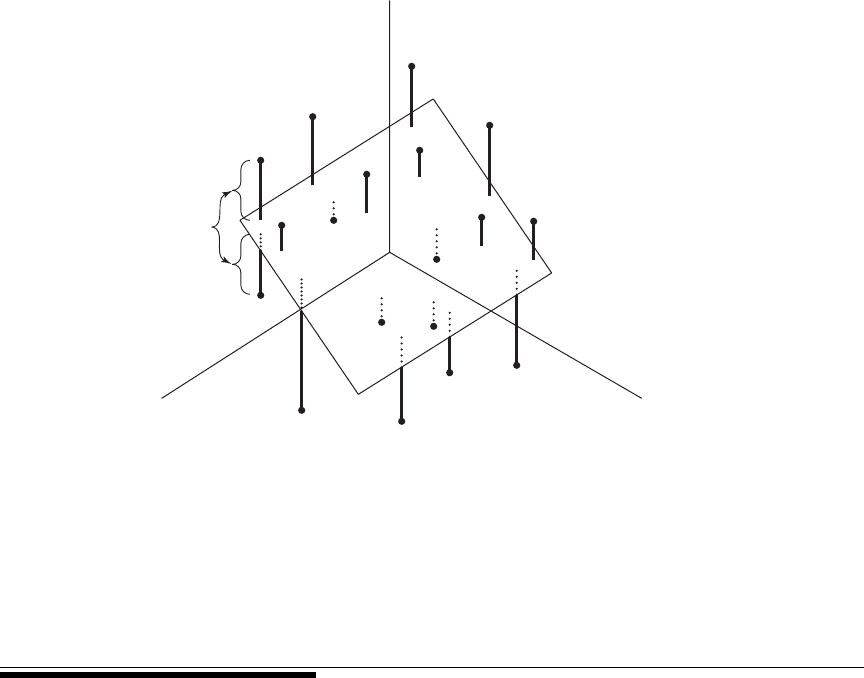
a plane in three-dimensional space may be ﬁtted to the data points as illustrated in Fig-

ure 10.2.1. When the model contains more than two independent variables, it is described

geometrically as a hyperplane.

In Figure 10.2.1 the observer should visualize some of the points as being located

above the plane and some as being located below the plane. The deviation of a point

from the plane is represented by

(10.2.3)

In Equation 10.2.2, represents the point where the plane cuts the Y-axis; that

is, it represents the Y-intercept of the plane. measures the average change in Y for ab

= y

- b

= b

+ b

, X

, Á X

;

, x

, Á , x

= b

+ b

...

+ b

10.2 THE MULTIPLE LINEAR REGRESSION MODEL

487

unit change in when remains unchanged, and measures the average change in

Y for a unit change in when remains unchanged. For this reason and are

referred to as partial regression coefﬁcients.

10.3 OBTAINING THE MULTIPLE

REGRESSION EQUATION

Unbiased estimates of the parameters of the model speciﬁed in Equation

10.2.1 are obtained by the method of least squares. This means that the sum of the

squared deviations of the observed values of Y from the resulting regression surface is

minimized. In the three-variable case, as illustrated in Figure 10.2.1, the sum of the

squared deviations of the observations from the plane are a minimum when and

are estimated by the method of least squares. In other words, by the method of least

squares, sample estimates of are selected in such a way that the quantity

is minimized. This quantity, referred to as the sum of squares of the residuals, may also

be written as

(10.3.1)

indicating the fact that the sum of squares of deviations of the observed values of Y from

the values of Y calculated from the estimated equation is minimized.

= g1y

- yN

= g1y

- b

...

- b

, b

, . . . , b

, b

, . . . , b

488 CHAPTER 10 MULTIPLE REGRESSION AND CORRELATION

Deviations from the

plane

Regression plane

FIGURE 10.2.1 Multiple regression plane and scatter of points.

Estimates of the multiple regression parameters may be obtained by means of arith-

metic calculations performed on a handheld calculator. This method of obtaining the esti-

mates is tedious, time-consuming, subject to errors, and a waste of time when a computer is

available. Those interested in examining or using the arithmetic approach may consult ear-

lier editions of this text or those by Snedecor and Cochran (1) and Steel and Torrie (2), who

give numerical examples for four variables, and Anderson and Bancroft (3), who illustrate

the calculations involved when there are ﬁve variables. In the following example we use SPSS

software to illustrate an interesting graphical summary of sample data collected on three vari-

ables. We then use MINITAB to illustrate the application of multiple regression analysis.

EXAMPLE 10.3.1

Researchers Jansen and Keller (A-1) used age and education level to predict the capac-

ity to direct attention (CDA) in elderly subjects. CDA refers to neural inhibitory mech-

anisms that focus the mind on what is meaningful while blocking out distractions. The

study collected information on 71 community-dwelling older women with normal men-

tal status. The CDA measurement was calculated from results on standard visual and

auditory measures requiring the inhibition of competing and distracting stimuli. In this

study, CDA scores ranged from to 9.61 with higher scores corresponding with

better attentional functioning. The measurements on CDA, age in years, and education

level (years of schooling) for 71 subjects are shown in Table 10.3.1. We wish to obtain

the sample multiple regression equation.

-7.65

10.3 OBTAINING THE MULTIPLE REGRESSION EQUATION 489

(

Continued

)

TABLE 10.3.1 CDA Scores, Age, and Education Level

for 71 Subjects Described in Example 10.3.1

Age Ed-Level CDA Age Ed-Level CDA

72 20 4.57 79 12 3.17

68 12 3.04 87 12 1.19

65 13 1.39 71 14 0.99

85 14 3.55 81 16 2.94

84 13 2.56 66 16 2.21

90 15 4.66 81 16 0.75

79 12 2.70 80 13 5.07

74 10 0.30 82 12 5.86

69 12 4.46 65 13 5.00

87 15 6.29 73 16 0.63

84 12 4.43 85 16 2.62

79 12 0.18 83 17 1.77

71 12 1.37 83 8 3.79

76 14 3.26 76 20 1.44

73 14 1.12 77 12 5.77

86 12 0.77 83 12 5.77

69 17 3.73 79 14 4.62

66 11 5.92 69 12 2.03

65 16 5.74 66 14 2.22

Prior to analyzing the data using multiple regression techniques, it is useful to con-

struct plots of the relationships among the variables. This is accomplished by making

separate plots of each pair of variables, (X1, X2), (X1, Y), and (X2, Y ). A software pack-

age such as SPSS displays each combination simultaneously in a matrix format as

shown in Figure 10.3.1. From this ﬁgure it is apparent that we should expect a negative

490

CHAPTER 10 MULTIPLE REGRESSION AND CORRELATION

Age Ed-Level CDA Age Ed-Level CDA

71 14 2.83 75 12 0.80

80 18 2.40 77 16 0.75

81 11 0.29 78 12 4.60

66 14 4.44 83 20 2.68

76 17 3.35 85 10 3.69

70 12 3.13 76 18 4.85

76 12 2.14 75 14 0.08

67 12 9.61 70 16 0.63

72 20 7.57 79 16 5.92

68 18 2.21 75 18 3.63

102 12 2.30 94 8 7.07

67 12 1.73 76 18 6.39

66 14 6.03 84 18 0.08

75 18 0.02 79 17 1.07

91 13 7.65 78 16 5.31

74 15 4.17 79 12 0.30

90 15 0.68

Source: Debra A. Jansen, Ph.D., R.N. Used with permission.

FIGURE 10.3.1 SPSS matrix scatter plot of the

data in Table 10.3.1.

10.3 OBTAINING THE MULTIPLE REGRESSION EQUATION 491

Dialog box: Session command:

Stat ➤ Regression ➤ Regression MTB > Name C4 = `SRES1’

Type Y in Response and X1 X2 C5 = `FITS1’ C6 = `RESI1’

in Predictors. MTB > Regress `y’ 2 `x1’ `x2’;

Check Residuals. SUBC> SResiduals `SRES1’;

Check Standard resids. SUBC> Fits `FITS1’;

Check OK. SUBC> Constant;

SUBC> Residuals `RESI1’.

Output:

Regression Analysis: Y versus X1, X2

The regression equation is

Y = 5.49 - 0.184 X1 + 0.611 X2

Predictor Coef SE Coef T P

Constant 5.494 4.443 1.24 0.220

X1 -0.18412 0.04851 -3.80 0.000

X2 0.6108 0.1357 4.50 0.000

S = 3.134 R-Sq = 37.1% R-Sq (adj) = 35.2%

Analysis of Variance

Source DF SS MS F P

Regression 2 393.39 196.69 20.02 0.000

Residual Error 68 667.97 9.82

Total 70 1061.36

Source DF Seq SS

X1 1 194.24

X2 1 199.15

Unusual Observations

Obs X1 Y Fit SE Fit Residual St Resid

28 67 9.610 0.487 0.707 9.123 2.99R

31 102 -2.300 -5.957 1.268 3.657 1.28X

44 80 5.070 -1.296 0.425 6.366 2.05R

67 94 -7.070 -6.927 1.159 -0.143 -0.05X

R denotes an observation with a large standardized residual.

X denotes an observation whose X value gives it large inﬂuence.

FIGURE 10.3.2 MINITAB procedure and output for Example 10.3.1.

492 CHAPTER 10 MULTIPLE REGRESSION AND CORRELATION

The REG Procedure

Model: MODEL1

Dependent Variable: CDA

Analysis of Variance

Sum of Mean

Source DF Squares Square F Value Pr > F

Model 2 393.38832 196.69416 20.02 <.0001

Error 68 667.97084 9.82310

Corrected Total 70 1061.35915

Root MSE 3.13418 R-Square 0.3706

Dependent Mean 0.00676 Adj R-Sq 0.3521

Coeff Var 46360

Parameter Estimates

Parameter Standard

Variable DF Estimate Error t Value Pr > |t|

Intercept 1 5.49407 4.44297 1.24 0.2205

AGE 1 -0.18412 0.04851 -3.80 0.0003

EDUC 1 0.61078 0.13565 4.50 <.0001

FIGURE 10.3.3 SAS

output for Example 10.3.1.

relationship between CDA and Age and a positive relationship between CDA and Ed-

Level. We shall see that this is indeed the case when we use MINITAB to analyze the

data.

Solution: We enter the observations on age, education level, and CDA in c1 through

c3 and name them X1, X2, and Y, respectively. The MINITAB dialog box

and session command, as well as the output, are shown in Figure 10.3.2.

We see from the output that the sample multiple regression equation, in the

notation of Section 10.2, is

Other output entries will be discussed in the sections that follow.

The SAS output for Example 10.3.1 is shown in Figure 10.3.3. ■

After the multiple regression equation has been obtained, the next step involves its

evaluation and interpretation. We cover this facet of the analysis in the next section.

= 5.49 - .184x

+ .611x

EXERCISES

Obtain the regression equation for each of the following data sets.

10.3.1 Machiel Naeije (A-2) studied the relationship between maximum mouth opening and measurements

of the lower jaw (mandible). He measured the dependent variable, maximum mouth opening (MMO,

measured in mm), as well as predictor variables, mandibular length (ML, measured in mm) and

angle of rotation of the mandible (RA, measured in degrees) of 35 subjects.

MMO (Y) ML (X

) RA (X

) MMO (Y) ML (X

) RA (X

)

52.34 100.85 32.08 50.82 90.65 38.33

51.90 93.08 39.21 40.48 92.99 25.93

52.80 98.43 33.74 59.68 108.97 36.78

50.29 102.95 34.19 54.35 91.85 42.02

57.79 108.24 35.13 47.00 104.30 27.20

49.41 98.34 30.92 47.23 93.16 31.37

53.28 95.57 37.71 41.19 94.18 27.87

59.71 98.85 44.71 42.76 89.56 28.69

53.32 98.32 33.17 51.88 105.85 31.04

48.53 92.70 31.74 42.77 89.29 32.78

51.59 88.89 37.07 52.34 92.58 37.82

58.52 104.06 38.71 50.45 98.64 33.36

62.93 98.18 43.89 43.18 83.70 31.93

57.62 91.01 41.06 41.99 88.46 28.32

65.64 96.98 41.92 39.45 94.93 24.82

52.85 97.85 35.25 38.91 96.81 23.88

64.43 96.89 45.11 49.10 93.13 36.17

57.25 98.35 39.44

Source: M. Naeije, D.D.S. Used with permission.

10.3.2 Family caregiving of older adults is more common in Korea than in the United States. Son et al.

(A-3) studied 100 caregivers of older adults with dementia in Seoul, South Korea. The dependent

variable was caregiver burden as measured by the Korean Burden Inventory (KBI). Scores ranged

from 28 to 140, with higher scores indicating higher burden. Explanatory variables were indexes

that measured the following:

ADL: total activities of daily living (low scores indicate that the elderly perform activities

independently).

MEM: memory and behavioral problems (higher scores indicate more problems).

COG: cognitive impairment (lower scores indicate a greater degree of cognitive impairment).

The reported data are as follows:

KBI (Y ) ADL (X

) MEM (X

) COG (X

) KBI (Y) ADL (X

) MEM (X

) COG (X

)

28 39 4 18 88 76 50 5

68 52 33 9 54 79 44 11

59 89 17 3 73 48 57 9

91 57 31 7 87 90 33 6

EXERCISES 493

(Continued)

KBI (Y ) ADL (X

) MEM (X

) COG (X

) KBI (Y) ADL (X

) MEM (X

) COG (X

)

70 28 35 19 47 55 11 20

38 34 3 25 60 83 24 11

46 42 16 17 65 50 21 25

57 52 6 26 57 44 31 18

89 88 41 13 85 79 30 20

48 90 24 3 28 24 5 22

74 38 22 13 40 40 20 17

78 83 41 11 87 35 15 27

43 30 9 24 80 55 9 21

76 45 33 14 49 45 28 17

72 47 36 18 57 46 19 17

61 90 17 0 32 37 4 21

63 63 14 16 52 47 29 3

77 34 35 22 42 28 23 21

85 76 33 23 49 61 8 7

31 26 13 18 63 35 31 26

79 68 34 26 89 68 65 6

92 85 28 10 67 80 29 10

76 22 12 16 43 43 8 13

91 82 57 3 47 53 14 18

78 80 51 3 70 60 30 16

103 80 20 18 99 63 22 18

99 81 20 1 53 28 9 27

73 30 7 17 78 35 18 14

88 27 27 27 112 37 33 17

64 72 9 0 52 82 25 13

52 46 15 22 68 88 16 0

71 63 52 13 63 52 15 0

41 45 26 18 49 30 16 18

85 77 57 0 42 69 49 12

52 42 10 19 56 52 17 20

68 60 34 11 46 59 38 17

57 33 14 14 72 53 22 21

84 49 30 15 95 65 56 2

91 89 64 0 57 90 12 0

83 72 31 3 88 88 42 6

73 45 24 19 81 66 12 23

57 73 13 3 104 60 21 7

69 58 16 15 88 48 14 13

81 33 17 21 115 82 41 13

71 34 13 18 66 88 24 14

91 90 42 6 92 63 49 5

48 48 7 23 97 79 34 3

94 47 17 18 69 71 38 17

57 32 13 15 112 66 48 13

49 63 32 15 88 81 66 1

Source: Gwi-Ryung Son, R.N., Ph.D. Used with permission.

494 CHAPTER 10 MULTIPLE REGRESSION AND CORRELATION

10.3.3 In a study of factors thought to be related to patterns of admission to a large general hospital, an

administrator obtained these data on 10 communities in the hospital’s catchment area:

Index of

Persons per 1000 Availability of

Population Admitted Other Health Index of

During Study Period Services Indigency

Community (Y)(X

)(X

)

1 61.6 6.0 6.3

2 53.2 4.4 5.5

3 65.5 9.1 3.6

4 64.9 8.1 5.8

5 72.7 9.7 6.8

6 52.2 4.8 7.9

7 50.2 7.6 4.2

8 44.0 4.4 6.0

9 53.8 9.1 2.8

10 53.5 6.7 6.7

Total 571.6 69.9 55.6

10.3.4 The administrator of a general hospital obtained the following data on 20 surgery patients during

a study to determine what factors appear to be related to length of stay:

Postoperative Preoperative

Length of Number of Current Length of

Stay in Days Medical Problems Stay in Days

(Y)(X

)(X

)

611

621

11 2 2

913

16 3 3

16 1 5

411

831

11 2 2

13 3 2

13 1 4

912

17 3 3

17 2 4

12 4 1

611

511

EXERCISES 495

(Continued)

Postoperative Preoperative

Length of Number of Current Length of

Stay in Days Medical Problems Stay in Days

(Y)(X

)(X

)

12 3 2

812

922

Total 208 38 43

10.3.5 A random sample of 25 nurses selected from a state registry yielded the following information on

each nurse’s score on the state board examination and his or her ﬁnal score in school. Both scores

relate to the nurse’s area of afﬁliation. Additional information on the score made by each nurse

on an aptitude test, taken at the time of entering nursing school, was made available to the

researcher. The complete data are as follows:

State Board Score Final Score Aptitude Test Score

(Y )(X

)(X

)

440 87 92

480 87 79

535 87 99

460 88 91

525 88 84

480 89 71

510 89 78

530 89 78

545 89 71

600 89 76

495 90 89

545 90 90

575 90 73

525 91 71

575 91 81

600 91 84

490 92 70

510 92 85

575 92 71

540 93 76

595 93 90

525 94 94

545 94 94

600 94 93

625 94 73

Total 13,425 2263 2053

496 CHAPTER 10 MULTIPLE REGRESSION AND CORRELATION