Dan B. Marghitu, Mechanisms and Robots Analysis with MATLAB®

Подождите немного. Документ загружается.

44 3 Velocity and Acceleration Analysis

A reference frame that moves with the rigid body is a body-ﬁxed (or rotating)

reference frame. The unit vectors ı, j

, and k of the body-ﬁxed reference frame are

not constant, because they rotate with the body-ﬁxed reference frame. The location

of the point O is arbitrary.

The position vector of a point M, M ∈ (RB), with respect to the ﬁxed reference

frame x

is denoted by r

= r

and with respect to the rotating reference

frame Oxyz is denoted by r = r

. The location of the origin O of the rotating

reference frame with respect to the ﬁxed point O

is deﬁned by the position vector

= r

. Then, the relation between the vectors r

, r and r

is given by

= r

+ r = r

+ x ı + y j + zk, (3.1)

where x, y, and z represent the projections of the vector r = r

on the rotating

reference frame r = xı + y j

+ zk.

The magnitude of the vector r = r

is a constant as the distance between the

points O and M is constant, O ∈ (RB), and M ∈ (RB). Thus, the x, y and z compo-

nents of the vector r with respect to the rotating reference frame are constant. The

unit vectors ı, j

, and k are time-dependent vector functions. The vectors ı, j and k

are the unit vector of an orthogonal Cartesian reference frame, thus one can write

ı ·ı = 1, j

·j = 1, k ·k = 1, (3.2)

ı ·j

= 0, j ·k = 0, k ·ı = 0. (3.3)

3.2 Velocity Field for a Rigid Body

The velocity of an arbitrary point M of the rigid body with respect to the ﬁxed

reference frame x

, is the derivative with respect to time of the position vector r

v =

= v

+ x

dı

+ y

+ z

ı +

k, (3.4)

where v

represent the velocity of the origin of the rotating reference frame

with respect to the ﬁxed reference frame Oxyz. Because all the points in

the rigid body maintain their relative position, their velocity relative to the rotating

reference frame xyz is zero, i.e., ˙x = ˙y = ˙z = 0.

The velocity of point M is

v = v

+ x

dı

+ y

+ z

= v

+ x i + y j + z

The derivative of the Eqs. 3.2 and 3.3 with respect to time gives

3.2 Velocity Field for a Rigid Body 45

dı

·ı = 0,

·j

= 0,

·k = 0, (3.5)

and

dı

·j

+ ı ·

= 0,

·k + j

= 0,

·ı + k ·

dı

= 0. (3.6)

For Eq. 3.6 the following notation is used

dı

·j

= −ı ·

= ω

·k = −j

= ω

·ı = −k ·

dı

= ω

, (3.7)

where ω

, ω

and ω

may be considered as the projections of a vector ω

= ω

ı + ω

j + ω

To calculate

dı

the relation for an arbitrary vector v will be used

v = v

ı + v

j + v

k =(v ·ı)ı +(v ·j)j +(v ·k) k. (3.8)

Using Eq. 3.8 and the results from Eqs. 3.5 and 3.6 one can write

dı



dı

·ı



ı +



dı

·j





dı

·k



=(0)ı +(ω

)j −(ω



ıj

100



ω ×ı,



·ı



ı +



·j





·k



=(−ω

)ı +(0)j +(ω



ıj

010



ω ×j,



·ı



ı +



·j





·k



k (3.9)

=(ω

)ı −(ω

)j +(0)k

46 3 Velocity and Acceleration Analysis



ıj

001



ω ×k.

The relations

dı

ω ×ı,

ω ×j,

ω ×k. (3.10)

are known as Poisson formulas and

ω is the angular velocity vector. Using Eqs. 3.4

and 3.10 the velocity of the point M on the rigid body is

v = v

+ x ω ×ı + y ω ×j + zω ×k = v

+ ω ×(xı + y j + zk),

v = v

+ ω ×r. (3.11)

Combining Eqs. 3.4 and 3.11 it results that

r =

ω ×r. (3.12)

Using Eq. 3.11 one can write the components of the velocity as

= v

+ zω

−yω

= v

+ x ω

−zω

= v

+ yω

−x ω

The relation between the velocities v

and v

of two points M and O on the rigid

body is

= v

+ ω ×r

, (3.13)

= v

+ v

rel

, (3.14)

where v

rel

is the relative velocity, for rotational motion, of M with respect to O and

is given by

rel

= v

= ω ×r

. (3.15)

The relative velocity v

is perpendicular to the position vector r

, v

⊥ r

and has the direction given by the angular velocity vector

ω. The magnitude of the

relative velocity is |v

| = v

= ω r

3.3 Acceleration Field for a Rigid Body

The acceleration of an arbitrary point M ∈(RB) with respect to a ﬁxed reference

frame O

, represents the double derivative with respect to time of the position

vector r

3.3 Acceleration Field for a Rigid Body 47

a =

v =

+ ω ×r)=

×r +

ω ×

ω ×r + ω ×

r. (3.16)

The acceleration of the point O with respect to the ﬁxed reference frame O

. (3.17)

The derivative of the vector

ω with respect to the time is the angular acceleration

vector

α given by

α =

dω

ı +

dω

k + ω

dı

+ ω

= α

ı + α

j + α

k + ω

ω ×ı + ω

ω ×j + ω

ω ×k

= α

ı + α

+ α

k + ω ×ω =α

ı + α

j + α

k, (3.18)

where α

dω

, α

dω

, and α

dω

. In the previous expression the Poisson

formulas have been used. Using Eqs. 3.16–3.18 the acceleration of the point M is

a = a

+ α ×r + ω ×(ω ×r). (3.19)

Using Eq. 3.19 the components of the acceleration are

= a

+(z α

−yα

)+ω

(yω

−x ω

)+ω

(x ω

−x ω

= a

+(x α

−zα

)+ω

(zω

−yω

)+ω

(x ω

−yω

= a

+(y α

−x α

)+ω

(x ω

−zω

)+ω

(yω

−zω

The relation between the accelerations a

and a

of two points M and O on the

rigid body is

= a

+ α ×r

+ ω ×(ω ×r

). (3.20)

In the case of planar motion

ω ×(ω ×r

)=−ω

and Eq. 3.20 becomes

= a

+ α ×r

−ω

. (3.21)

Equation 3.21 can be written as

= a

+ a

rel

, (3.22)

where a

rel

is the relative acceleration, for rotational motion, of M with respect to O

and is given by

rel

= a

+ a

. (3.23)

48 3 Velocity and Acceleration Analysis

The normal relative acceleration of M with respect to O is

= ω ×(ω ×r

), (3.24)

is parallel to the position vector r

, a

||r

, and has the direction towards the

center of rotation, from M to O. The magnitude of the normal relative acceleration

| = a

= ω

The tangential relative acceleration of M with respect to O

= α ×r

, (3.25)

is perpendicular to the position vector r

, a

⊥r

, and has the direction given

by the angular aceeleration

α. The magnitude of the normal relative acceleration is

| = a

= α r

Remarks:

1. If the orientation of a rigid body (RB) in a reference frame RF

depends on only

a single scalar variable

ζ, there exists for each value of ζ a vector ω such that the

derivative with respect to

ζ in RF

of every vector c ﬁxed in the rigid body (RB)

is given by

d c

dζ

= ω ×c, (3.26)

where the vector

ω is the rate of change of orientation of the rigid body (RB) in

the reference frame RF

with respect to ζ. The vector ω is given by

ω =

d a

dζ

d b

dζ

d a

dζ

·b

, (3.27)

where a and b are any two non-parallel vectors ﬁxed in the rigid body (RB). The

vector

ω is a free vector, i.e. is not associated with any particular point. With

the help of

ω one can replace the process of differentiation with that of cross

multiplication. The vector

ω may be expressed in a symmetrical relation in a and

ω =

⎛

⎜

⎝

d a

dζ

d b

dζ

d a

dζ

·b

d b

dζ

d a

dζ

d b

dζ

·a

⎞

⎟

⎠

. (3.28)

3.3 Acceleration Field for a Rigid Body 49

2. The ﬁrst derivatives of a vector p with respect to a scalar variable ζ in two refer-

ence frames RF

and RF

are related as follows

( j)

d p

dζ

(i)

d p

dζ

+ ω

×p, (3.29)

where

is the rate of change of orientation of RF

in RF

with respect to ζ and

( j)

d p

dζ

is the total derivative of p with respect to ζ in RF

3. The angular velocity of a rigid body (RB) in a reference frame RF

is the rate of

change of orientation with respect to the time t

ω =

⎛

⎜

⎝

d a

d b

d a

·b

d b

d a

d b

·a

⎞

⎟

⎠



a ×

a ·b

b ×

b ·a



The direction of

ω is related to the direction of the rotation of the rigid body

through a right-hand rule.

4. Let RF

, i = 1,2,...,n be n reference frames. The angular velocity of a rigid body

r in the reference frame RF

, can be expressed as

= ω

+ ω

+ ... + ω

r,n−1

Proof

Let p be any vector ﬁxed in the rigid body. Then,

(i)

d p

×p

(i−1)

d p

r,i−1

×p.

On the other hand,

(i)

d p

(i−1)

d p

i,i−1

×p.

Hence,

×p = ω

r,i−1

×p + ω

i,i−1

×p,

as this equation is satisﬁed for all p ﬁxed in the rigid body

= ω

r,i−1

+ ω

i,i−1

. (3.30)

With i = n, Eq. 3.30 gives

= ω

r,n−1

+ ω

n,n−1

. (3.31)

50 3 Velocity and Acceleration Analysis

With i = n −1, Eq. 3.30 gives

r,n−1

= ω

r,n−2

+ ω

n−1,n−2

. (3.32)

Substitute Eq. 3.32 into Eq. 3.31

= ω

r,n−2

+ ω

n−1,n−2

+ ω

n,n−1

Next use Eq. 3.30 with i = n −2, then with i = n −3, and so forth.

3.4 Motion of a Point that Moves Relative to a Rigid Body

A reference frame that moves with the rigid body is a body-ﬁxed reference frame.

Figure 3.2 shows a rigid body (RB) in motion relative to a primary reference frame

with its origin at point O

, x

. The primary reference frame is a ﬁxed reference

frame or an Earth-ﬁxed reference frame. The unit vectors ı

, and k

of the primary

reference frame are constant.

A(xyz)

=2ω × v

A(xyz)

r =

(RB)

cor

rel

Fig. 3.2 Rigid body in motion; the point A is not assumed to be a point of the rigid body, A /∈(RB)

3.4 Motion of a Point that Moves Relative to a Rigid Body 51

The body-ﬁxed reference frame, xyz, has its origin at a point O of the rigid body

(O ∈ (RB)), and is a moving reference frame relative to the primary reference. The

unit vectors ı,j

, and k of the body-ﬁxed reference frame are not constant, because

they rotate with the body-ﬁxed reference frame.

The position vector of a point P of the rigid body (P ∈(RB)) relative to the origin,

O, of the body-ﬁxed reference frame is the vector r

. The velocity of P relative to

O is

= v

rel

= ω ×r

where

ω is the angular velocity vector of the rigid body.

The position vector of a point A (the point A is not assumed to be a point of the

rigid body, A /∈ (RB)), relative to the origin O

of the primary reference frame is,

Fig. 3.1,

= r

+ r,

where

r = r

= x ı + y j + zk

is the position vector of A relative to the origin O, of the body-ﬁxed reference frame,

and x,y, and z are the coordinates of A in terms of the body-ﬁxed reference frame.

The velocity of the point A is the time derivative of the position vector r

= v

+ v

rel

= v

ı + x

dı

+ y

k + z

Using Poisson formulas, the total derivative of the position vector r is

r = ˙x ı + ˙yj

+ ˙zk + ω ×r.

The velocity of A relative to the body-ﬁxed reference frame is a derivative in the

body-ﬁxed reference frame

rel

A(xyz)

(xyz)

d r

ı +

k = ˙xı + ˙yj

+ ˙zk. (3.33)

A general formula for the total derivative of a moving vector r may be written as

(xyz)

d r

ω ×r, (3.34)

52 3 Velocity and Acceleration Analysis

where

(0)

d r

is the derivative in the ﬁxed (primary) reference frame (0)

), and

(xyz)

d r

is the derivative in the rotating (mobile or body-ﬁxed) ref-

erence frame (xyz).

The velocity of the point A relative to the primary reference frame is

= v

+ v

rel

A(xyz)

+ ω ×r. (3.35)

Equation 3.35 expresses the velocity of a point A as the sum of three terms:

• the velocity of a point O of the rigid body;

• the velocity v

rel

A(xyz)

of A relative to the rigid body; and

• the velocity

ω ×r of A relative to O due to the rotation of the rigid body.

The acceleration of the point A relative to the primary reference frame is obtained

by taking the time derivative of Eq. 3.35

= a

+ a

= a

+ a

rel

A(xyz)

+ 2ω ×v

rel

A(xyz)

+ α ×r + ω ×(ω ×r), (3.36)

where

rel

A(xyz)

(xyz)

ı +

j +

k (3.37)

is the acceleration of A relative to the body-ﬁxed reference frame or relative to the

rigid body. The term

cor

A(xyz)

= 2ω ×v

rel

A(xyz)

is called the Coriolis acceleration. The direction of the Coriolis acceleration is ob-

tained by rotating the linear relative velocity v

rel

A(xyz)

through 90

◦

in the direction of

rotation given by

ω.

In the case of planar motion, Eq. 3.36 becomes

= a

+ a

= a

+ a

rel

A(xyz)

+ 2ω ×v

rel

A(xyz)

+ α ×r −ω

r. (3.38)

The motion of the rigid body (RB) is described relative to the primary reference

frame. The velocity v

and the acceleration a

of a point A are relative to the pri-

mary reference frame. The terms v

rel

A(xyz)

and a

rel

A(xyz)

are the velocity and acceleration

of point A relative to the body-ﬁxed reference frame, i.e., they are the velocity and

acceleration measured by an observer moving with the rigid body, Fig. 3.2. If A is a

point of the rigid body, A ∈ (RB), v

rel

A(xyz)

= 0 and a

rel

A(xyz)

= 0.

Motion of a Point Relative to a Moving Reference Frame

The velocity and acceleration of an arbitrary point A relative to a point O of a rigid

body, in terms of the body-ﬁxed reference frame, are given by Eqs. 3.35 and 3.36

3.5 Slider-Crank (R-RRT) Mechanism 53

= v

+ v

rel

+ ω ×r

, (3.39)

= a

+ a

rel

+ 2ω ×v

rel

+ α ×r

+ ω ×(ω ×r

). (3.40)

These results apply to any reference frame having a moving origin O and rotating

with angular velocity

ω and angular acceleration α relative to a primary reference

frame (Fig. 3.2). The terms v

and a

are the velocity and acceleration of an ar-

bitrary point A relative to the primary reference frame. The terms v

rel

and a

rel

are

the velocity and acceleration of A relative to the secondary moving reference frame,

i.e., they are the velocity and acceleration measured by an observer moving with the

secondary reference frame. The Coriolis acceleration is a

cor

= 2ω ×v

rel

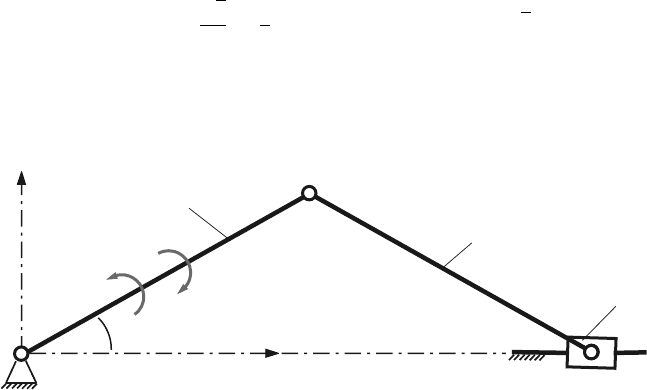
3.5 Slider-Crank (R-RRT) Mechanism

Exercise

The R-RRT (slider-crank) mechanism shown in Fig. 3.3 has the dimensions: AB =

1 m and BC = 1 m. When the driver link 1 makes an angle φ = φ

= π/6 rad with

the horizontal axis the instantaneous speed and the angular acceleration of the link

1 are ω=1 rad/s and α=–1 rad/s

Find the velocities and the accelerations of the joints and the angular velocities

and accelerations of the links for the given driver-link angle.

Solution

The point A is selected as the origin of the xyz reference frame. The position vectors

of the joints B and C are:

= x

ı + y

j =

√

ı +

m and r

= x

ı + y

j =

√

3ı + 0 j m.

The MATLAB



statements for the positions of the mechanism are:

AB=1; BC=1;

Fig. 3.3 Slider-crank (R-RRT) mechanism