Dan B. Marghitu, Mechanisms and Robots Analysis with MATLAB®

Подождите немного. Документ загружается.

104 3 Velocity and Acceleration Analysis

The sign of the relative angular velocities is selected arbitrarily positive. The numer-

ical computation will then give the correct orientation of the unknown vectors. The

components of the vectors r

and the angle φ

are already known from the position

analysis of the mechanism.

The unknown vectors with MATLAB commands are:

omega43v=[00sym(’omega43z’,’real’) ];

omega05v=[00sym(’omega05z’,’real’) ];

v54v = sym(’vD54’,’real’)

[ cos(phi4) sin(phi4) 0];

Equation 3.97 becomes

k + ω

k = 0,



ıj

00ω



ıj

00ω



+ v

cosφ

ı + v

sinφ

j = 0. (3.98)

Equation 3.98 projected onto the “ﬁxed” reference frame Oxyz gives

+ ω

= 0,

+ y

+ v

cosφ

= 0,

−x

+ v

sinφ

= 0. (3.99)

The above system of equations using the following MATLAB commands becomes:

eqIIomega = omega30 + omega43v + omega05v;

eqIIvz=eqIIomega(3);

eqIIv=cross(rC,omega30)+cross(rD,omega43v)+v54v;

eqIIvx=eqIIv(1);

eqIIvy=eqIIv(2);

Equation 3.99 represents an algebraic system of three equations with three un-

knowns: ω

, ω

, and v

. The system is solved using the MATLAB commands:

solIIv=solve(eqIIvz,eqIIvx,eqIIvy);

omega43=[00eval(solIIv.omega43z) ];

omega05=[00eval(solIIv.omega05z) ] ;

vD5D4 = eval(solIIv.vD54)

[ cos(phi4) sin(phi4) 0];

The following numerical solutions are obtained:

= −1.50912 rad/s, ω

= −2.97887 rad/s, and v

= 0.338367 m/s.

To print the numerical values with MATLAB, the following commands are used:

3.10 Independent Contour Equations 105

fprintf(’omega43 = [ %g, %g, %g] (rad/s)\n’, omega43)

fprintf(’omega05 = [ %g, %g, %g] (rad/s)\n’, omega05)

fprintf(’vD54 = %g (m/s)\n’, eval(solIIv.vD54))

fprintf(’vD5D4 = [ %g, %g, %d] (m/s)\n’, vD5D4)

The absolute angular velocities of the links 4 and 5 are

= ω

= −ω

= 2.97887k rad/s,

and with MATLAB commands, they are:

omega50 = - omega05;

omega40 = omega50;

fprintf(’omega40=omega50=[%d,%d,%g] (rad/s)\n’,...

omega50)

For the acceleration analysis, the following vectorial equations are used:

+ α

= 0,

×α

+ r

×α

+ r

×α

+ a

rel

+ a

cor

−ω

= 0, (3.100)

where

= α

k, α

= α

k, α

= α

rel

= a

cosφ

ı + a

sinφ

cor

= 2ω

×v

The unknown acceleration vectors using the MATLAB commands are:

alpha43v=[00sym(’alpha43z’,’real’) ];

alpha05v=[00sym(’alpha05z’,’real’) ];

a54v = sym(’aD54’,’real’)

[ cos(phi4) sin(phi4) 0];

Equation 3.100 becomes

k + α

k = 0,



ıj

00α



ıj

00α



+ a

cosφ

ı + a

sinφ



ıj

00ω

cosφ

sinφ



−ω

[(x

−x

)ı +(y

−y

)j]

−ω

[(x

−x

)ı +(y

−y

)j]=0. (3.101)

Equation 3.101 can be rewritten as

106 3 Velocity and Acceleration Analysis

+ α

= 0,

+ y

+ a

cosφ

−2ω

sinφ

−ω

−x

) −ω

(0 −x

)=0,

−x

+ a

sinφ

+ 2ω

cosφ

−ω

−y

) −ω

(0 −y

)=0. (3.102)

The contour acceleration equations using MATLAB commands are:

eqIIalpha = alpha30 + alpha43v + alpha05v;

eqIIaz=eqIIalpha(3);

eqIIa1=cross(rC,alpha30)+cross(rD,alpha43v)+a54v;

eqIIa2=2

cross(omega40,vD5D4);

eqIIa3=-dot(omega30,omega30)

(rD-rC)- ...

dot(omega40,omega40)

(-rD);

eqIIa=eqIIa1+eqIIa2+eqIIa3;

eqIIax=eqIIa(1); eqIIay=eqIIa(2);

The unknowns in Eq. 3.102 are α

, α

, and a

. To solve the system, the follow-

ing MATLAB command is used:

solIIa=solve(eqIIaz,eqIIax,eqIIay);

alpha43=[00eval(solIIa.alpha43z) ];

alpha05=[00eval(solIIa.alpha05z) ] ;

aD5D4 = eval(solIIa.aD54)

[ cos(phi4) sin(phi4) 0];

The following numerical solutions are obtained:

= −2.3424 rad/s

, α

= −12.1939 rad/s

, and a

= 1.97423 m/s

The MATLAB commands for displaying the solutions are:

fprintf(’alpha43 = [ %g, %g, %g] (rad/sˆ2)\n’,alpha43)

fprintf(’alpha05 = [ %g, %g, %g] (rad/sˆ2)\n’,alpha05)

fprintf(’aD54 = %g (m/sˆ2)\n’, eval(solIIa.aD54))

fprintf(’aD5D4 = [ %g, %g, %d] (m/sˆ2)\n’, aD5D4)

The absolute angular accelerations of the links 4 and 5 are

= α

= −α

= 12.1939k rad/s

and with MATLAB they are:

alpha50 = - alpha05;

alpha40 = alpha50;

3.10 Independent Contour Equations 107

fprintf(’alpha40=alpha50=[%d,%d,%g](rad/sˆ2)\n’,...

alpha50)

The MATLAB program and results for the velocity and acceleration analysis using

the contour method are given in Appendix B.9.

Chapter 4

Dynamic Force Analysis

4.1 Equation of Motion for General Planar Motion

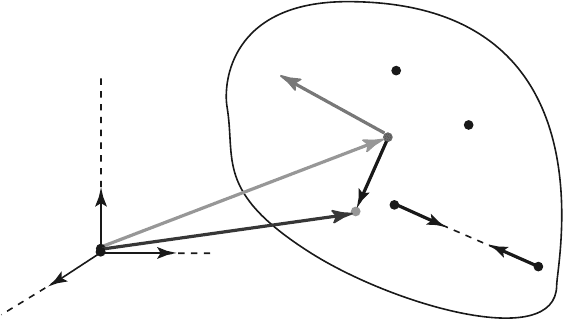
The friction effects in the joints are assumed to be negligible. Figure 4.1 shows an

arbitrary body with the total mass m. The body can be divided into n particles, the

ith particle having mass, m

, and the total mass is m =

∑

i=1

A rigid body can be considered as a collection of particles in which the number

of particles approaches inﬁnity and in which the distance between any two points

remains constant. As N approaches inﬁnity, each particle is treated as a differential

mass element, and the summation is replaced by integration over the body m =



dm. The position of the mass center of a collection of particles is deﬁned by

Fig. 4.1 Rigid body divided into particles

109

110 4 Dynamic Force Analysis

∑

i=1

or r



rdm, (4.1)

where r

= r

is the position vector from the origin O to the ith particle. The

time derivative of Eq. 4.1 gives

∑

i=1

= m

= ma

, (4.2)

where a

is the acceleration of the mass center. Any particle of the system is acted

on by two types of forces: internal forces (exerted by other particles that are also part

of the system) and external forces (exerted by a particle or object not included in the

system). Let f

be the internal force exerted on the jth particle by the ith particle.

Newton’s third law (action and reaction) states that the jth particle exerts a force

on the ith particle of equal magnitude, and opposite direction, and collinear with

the force exerted by the ith particle on the jth particle f

= −f

, j = i. Newton’s

second law for the ith particle must include all of the internal forces exerted by all

of the other particles in the system on the ith particle, plus the sum of any external

forces exerted by particles, objects outside of the system on the ith particle

∑

+ F

ext

= m

, j = i, (4.3)

where F

ext

is the external force on the ith particle. Equation 4.3 is written for each

particle in the collection of particles. Summing the resulting equations over all of

the particles from i = 1toN the following relation is obtained

∑

ext

= ma

, j = i. (4.4)

The sum of the internal forces includes pairs of equal and opposite forces. The sum

of any such pair must be zero. The sum of all of the internal forces on the collection

of particles is zero (Newton’s third law)

∑

= 0, j = i.

The term

∑

ext

is the sum of the external forces on the collection of particles

∑

ext

= F. The sum of the external forces acting on a closed system equals the

product of the mass and the acceleration of the mass center

= F. (4.5)

Equation 4.5 is Newton’s second law for a rigid body and is applicable to planar and

three-dimensional motions.

Resolving the sum of the external forces into Cartesian rectangular components

F = F

ı + F

j + F

4.1 Equation of Motion for General Planar Motion 111

and the position vector of the mass center

= x

(t)ı + y

(t)j + z

(t)k,

Newton’s second law for the rigid body is

= F, (4.6)

m ¨x

= F

, m ¨y

= F

, m ¨z

= F

. (4.7)

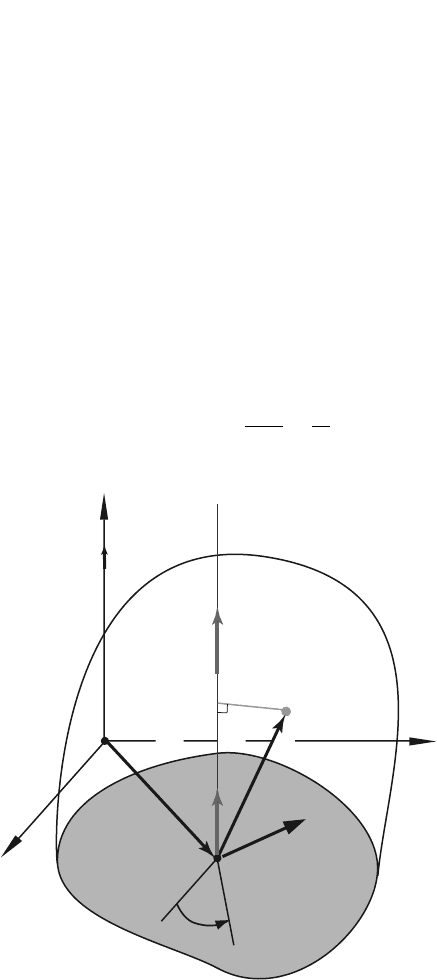
Figure 4.2 represents the rigid body moving with general planar motion in the (x,y)

plane. The origin of the Cartesian reference frame is O. The mass center C of the

rigid body is located in the plane of the motion. Let Oz be the axis through the ﬁxed

origin point O that is perpendicular to the plane of motion of the rigid body. Let Cz

be the parallel axis through the mass center C. The rigid body has a general planar

motion and the angular velocity vector is

ω = ωk. The sum of the moments about

O due to external forces and couples is

∑

[(r

×mv

)+H

]. (4.8)

α =

θk

Fig. 4.2 Rigid body moving with general planar motion in the (x, y) plane

112 4 Dynamic Force Analysis

The total angular momentum of the system about O is H

, the total angular momen-

tum of the system about C is H

, and v

is the velocity of C. The magnitude

of the angular momentum about Cz is H

∑

ω. The summation

∑

or the

integration over the body



dm is deﬁned as the mass moment of inertia I

of the

body about the z-axis through C

∑

The term r

is the perpendicular distance from d

to the P

particle. The mass mo-

ment of inertia I

is a constant property of the body and is a measure of the rota-

tional inertia or resistance to change in angular velocity due to the radial distribution

of the rigid body mass around the z-axis through C. The angular momentum of the

rigid body about Cz (z-axis through C)is

= I

ω or H

= I

ω k = I

ω.

Substituting this expression into Eq. 4.8 gives

∑

[(r

×mv

)+I

ω]=(r

×ma

)+I

α. (4.9)

The rotational equation of motion for the rigid body is

α =

∑

or I

α k =

∑

k. (4.10)

For general planar motion the angular acceleration is

α =

ω =

θ k, where the angle

θ describes the position, or orientation, of the rigid body about a ﬁxed axis. If the

rigid body is a plate moving in the plane of motion, the mass moment of inertia of

the rigid body about the z-axis through C becomes the polar mass moment of inertia

of the rigid body about C, I

= I

. For this case the Eq. 4.10 gives

α =

∑

. (4.11)

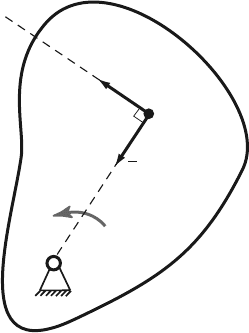
Consider the special case when the rigid body rotates about a ﬁxed point O as shown

in Fig. 4.3. The acceleration of the mass center is

= a

+ α ×r

−ω

= α ×r

−ω

The relation between the sum of the moments of the external forces about the ﬁxed

point O and the product I

α is given by Eq. 4.9

∑

= r

×ma

+ I

α,

∑

= r

×m(α ×r

−ω

)+I

4.1 Equation of Motion for General Planar Motion 113

Fig. 4.3 Rotation about a ﬁxed point O

= mr

×(α ×r

)+I

= m [(r

·r

)α −(r

·α)r

]+I

= mr

α + I

α =(mr

+ I

)α.

According to parallel-axis theorem

Ozz

= I

+ mr

where I

denotes the mass moment of inertia of the rigid body about the z-axis

through O. For the special case of rotation about a ﬁxed point O one can use the

formula

α =

∑

. (4.12)

The general equations of motion for a rigid body in plane motion are (Fig. 4.3)

F = ma

or F = m

∑

= I

α, (4.13)

or using the Cartesian components

m ¨x

∑

m ¨y

∑

θ =

∑

. (4.14)

Equations 4.13 and 4.14, also known as the Newton–Euler equations of motion, are

for plane motion, and are interpreted in two ways:

114 4 Dynamic Force Analysis

1. The forces and moments are known and the equations are solved for the motion

of the rigid body (direct dynamics).

2. The motion of the rigid body is known and the equations are solved for the forces

and moments (inverse dynamics).

The dynamic force analysis in this chapter is based on the known motion of the

mechanism.

4.2 D’Alembert’s Principle

Newton’s second law can be written as

F +(−m a

)=0, or F +F

= 0,

where the term F

= −m a

is the inertia force. Newton’s second law can be re-

garded as an “equilibrium” equation.

The total moment about a ﬁxed point O is

∑

=(r

×ma

)+I

α,

∑

+[r

×(−ma

)]+(−I

α)=0. (4.15)

The term M

= −I

α is the inertia moment. The sum of the moments about any

point, including the moment due to the inertial force −ma acting at the mass center

and the inertial moment, equals zero.

The equations of motion for a rigid body are analogous to the equations for static

equilibrium:

This is called D’Alembert’s principle. The dynamic force analysis is expressed

in a form similar to static force analysis

∑

F + F

= 0, (4.16)

∑

+ M

= 0, (4.17)

where

∑

F is the vector sum of all external forces (resultant of external force), and

∑

is the sum of all external moments about the center of mass C (resultant

external moment).

For a rigid body in plane motion in the (x, y) plane,

The sum of the forces equals zero and the sum of the moments about any point

equals zero when the inertial forces and moments are taken into account.