Dake L.P. Fundamentals of reservoir engineering
Подождите немного. Документ загружается.

STABILIZED INFLOW EQUATIONS 141
oh
rwf w h
w
oc
rh h e
h
q
r
pp ln r rr
2kh r
q
r
and p p ln r r r
2kh r
µ
π
µ
π
−= <≤
−= ≤<
and in particular
oh h
hwf
w
qr
pp ln
2kh r
µ
π
−=
(6.16)
oc e
eh
h
qr
and p p ln
2kh r
µ
π
−=
(6.17)
Since there is continuity of pressure at r = r
h
, then equs. (6.16) and (6.17) will yield,
upon addition
e
h
ewf oh oc
wh
oc oh eh
oc w h
r
rq
p p ln ln
2kh r r
qr
r
ln ln
2kh r r
µµ
π
µµ
πµ
æö
−= +
ç÷
èø
æö
=+
ç÷
èø
(6.18)
and since the inflow equation for an unstimulated well is
oc e
ewf
w
qr
pp ln
2kh r
µ
π
−=
Then the effect on the productivity index due to steam soaking can be expressed as
e
w
oh e
h
oc w h
PI stimulated well
PI ratio increase
PI unstimulated well
r
ln
r
r
r
ln ln
rr
µ
µ
=
=
+
and using typical field data in the above formula, i.e.
T
r
= 113° F T
s
= 525° F
µ
oc
= 980 cp
µ
oh
=3.2cp
r
e
= 382 ft r
h
=65 ft
r
w
=0.23ft
Then
382
In
.23
PI ratio increase 4.14
3.2 65 382
In In
980 .23 65
==
STABILIZED INFLOW EQUATIONS 142
This PI improvement is probably pessimistic since it has been assumed that steady
state conditions prevail from the start of production. In fact, transient flow is more likely
during the initial stage which will give an early boost to production, in excess of that
calculated from steady state considerations. The manner in which the early transient
part of the production cycle can be accounted for will be described in Chapter 9, sec. 6.
EXERCISE 6.1 WELLBORE DAMAGE
1) A homogeneous formation has an average effective permeability k
e
. The effective
permeability out to a radius r
a
from the well has been altered (damage/stimulation) so
that its average value in this region is k
a
. Show that, for this situation, the skin factor
may be expressed as
eaa
aw
kk r
SIn
kr
−
=
(6.19)
where r
w
is the wellbore radius. Assume that for r< r
a
, the flow can be approximately
described under steady state conditions and that for r >r
a
, semi-steady state.
2) During drilling, a well is damaged out to a radius of 4 ft from the wellbore so that the
permeability within the damaged zone is reduced to 1/100 th of the undamaged
effective permeability. After completion the well is stimulated so that the permeability
out to a distance of 10 ft from the wellbore is increased to ten times the undamaged
permeability. What will be the PI ratio increase if the wellbore radius is 0.333 ft and the
drainage radius 660 ft?
EXERCISE 6.1 SOLUTION
Pressure
k
e
r
w
r
a
k
a
p
a
p
wf
p
e
r
e
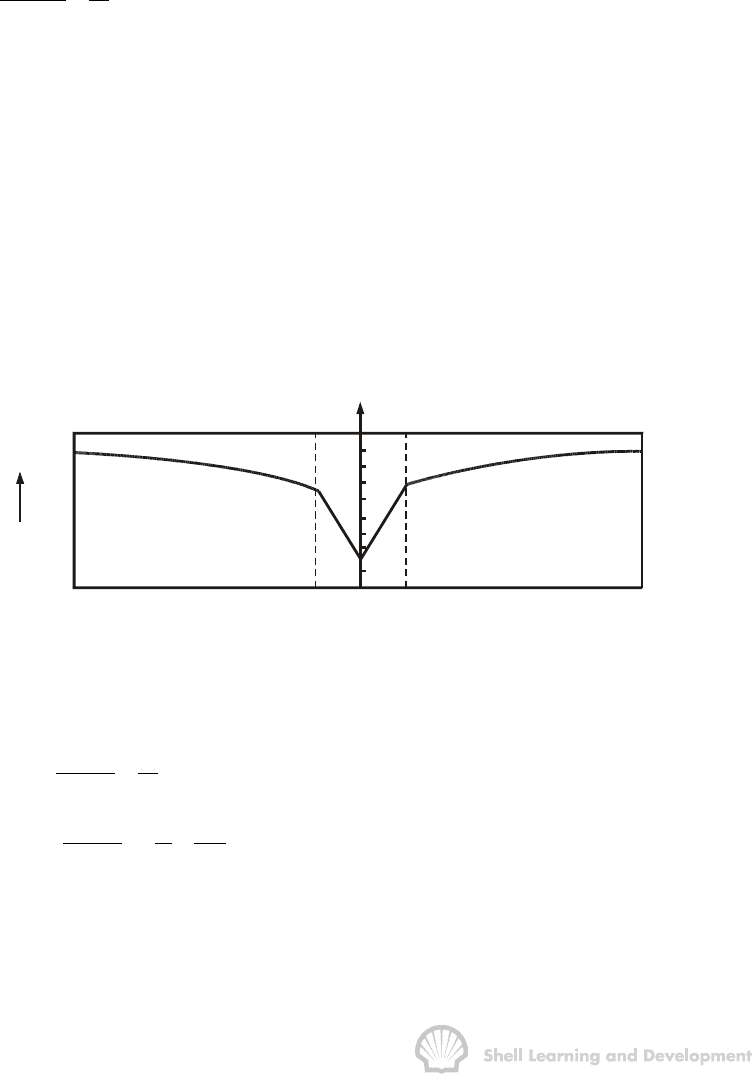
Fig. 6.3 Pressure profiles and geometry (Exercise 6.1)
1) The inflow equations appropriate for the pressure distribution shown in fig. 6.3 are
rwf w a
aw
2
ra a e
2
eae
qr
pp ln r rr
2kh r
qrr
pp ln rrr
2kh r
2r
µ
π
µ
π
−= <≤
æö
−= − ≤<
ç÷
èø
In particular

STABILIZED INFLOW EQUATIONS 143
a
awf
aw
r
q
pp ln
2kh r
µ
π
−=
and
e
ea
aa
r
q1
pp ln
2kh r 2
µ
π
æö
−= −
ç÷
èø
At r = r
a
, there is continuity of pressure, therefore, adding the above equations
eea
ewf
ea aw
eeeea
ew awaw
rkr
q1
p p ln ln
2kh r 2 k r
rrrkr
q1
ln ln ln ln
2kh r 2 r r k r
µ
π
µ
π
æö
−= −+
ç÷
èø
æö
=−+−+
ç÷
èø
i.e.
eea
ewf
ew a w
rkr
q1
pp ln 1ln
2khr2k r
µ
π
æö
æö
−= −+−
ç÷
ç÷
ç÷
èø
èø
which must be equivalent to
e
ewf
ew
r
q1
pp ln S
2kh r 2
µ
π
æö
−= −+
ç÷
èø
and therefore
eaa
aw
kk r
Sln
kr
−
=
which is an alternative expression for the skin factor presented by Craft and Hawkins
2
.
2) Before stimulation
1
4.333
S(1001)ln 254.02
0.333
=− =
while the skin factor after stimulation is
2
(1 10) 10.333
Sln 3.09
10 0.333
−
==−
and since
STABILIZED INFLOW EQUATIONS 144
e
e
w
2kh
PI
r
1
ln S
r2
π
µ
=
æö
−+
ç÷
èø
the Pl ratio increase is
660 1
ln 254.02
261.11
.333 2
660 1
4.00
ln 3.09
.333 2
65.3
−+
==
−−
=
6.5 GENERALIZED FORM OF INFLOW EQUATION UNDER SEMI-STEADY STATE
CONDITIONS
The semi-steady state inflow equation developed in sec. 6.2 appears to be restrictive in
that it only applies for a well producing from the centre of a circular shaped drainage
area. When a reservoir is producing under semi-steady state conditions each well will
assume its own fixed drainage boundary, as shown in fig. 5.3, and the shapes of these
may be far from circular. The inflow equation will therefore require some modification to
account for this lack of symmetry. Equation (6.12) can be expressed in a generalized
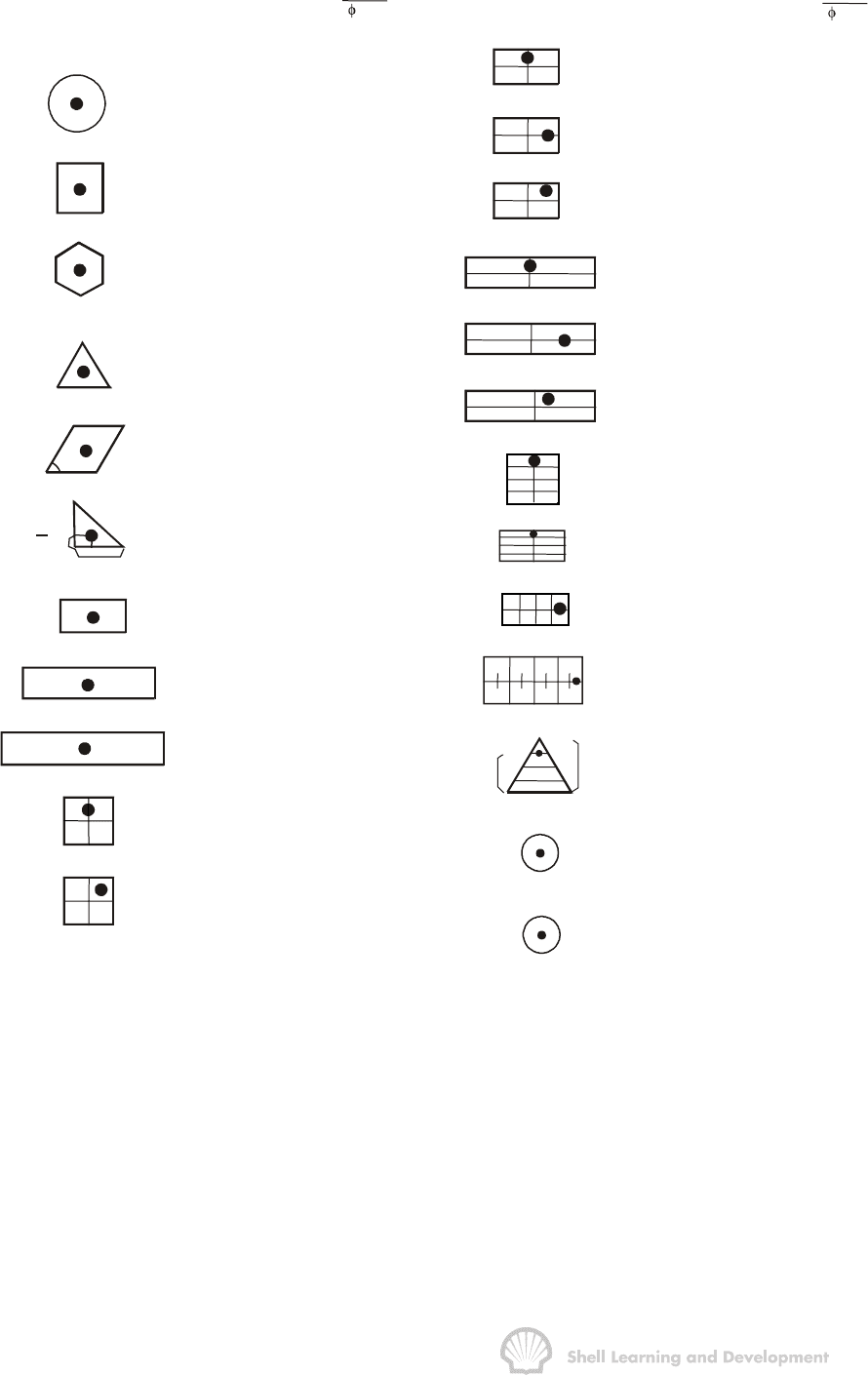
form by introducing the so-called Dietz shape factors
3
denoted by C
A
, which are
presented for a variety of different geometrical configurations in fig. 6.4. Precisely how
these shape factors were generated, in the first place, will be explained in the
appropriate place, Chapter 7, sec. 6. For the moment the reader is asked to accept the
following tenuous argument for the generalization of the inflow equation. Excluding the
mechanical skin factor, equ. (6.12) can be expressed as
2
e
wf
23/2
w
r
q1
pp ln
2kh 2 re
π
µ
ππ
æö
−=
ç÷
èø
(6.20)
in which the argument of the natural log can be modified as
2
e
3/2 2 2 2
www
4r
4A 4A
4 e r 56.32r 31.6r
π
πγ
== (6.21)
in which A is the area being drained, γ is the exponential of Euler's constant and is
equal to 1.781, and 31.6 is the Dietz shape factor for a well at the centre of a circle,
refer fig. 6.4. Therefore, equ. (6.20) can be expressed in the general form, including the
skin factor, as
wf
2
Aw
q14A
pp ln S
2kh 2 Cr
µ
πγ
æö
−= +
ç÷
èø
(6.22)
For a reservoir which is producing under semi-steady state conditions, then as already
noted, the volume drained by each well is directly proportional to the well's production
rate. Therefore, it is a fairly straightforward matter to estimate the volume being drained
by each well and, using the average thickness in the vicinity of the well, the area. If

STABILIZED INFLOW EQUATIONS 145
structural contour maps are available for the reservoir, then the areas so determined
can be roughly matched to the reservoir geometry to obtain a reasonable estimate of
the shape of the drainage area. Fig. 6.4 should then be consulted to determine the
shape factor C
A
which can be seen to be dependent not only on the drainage shape
but also upon the position of the well with respect to the boundary. For irregular
shapes, interpolation between the geometrical configurations presented by Dietz may
be necessary. Naturally it is never possible to obtain the exact shape of the drainage
volume but a reasonable estimate can usually be made which, when interpreted in
terms of a shape factor and used in equ. (6.22), can considerably improve the
accuracy of calculations made using the inflow equation.
Also listed in fig. 6.4 is the dimensionless time group t
DA
= kt/
φµ
cA, in which t is the
time for which the well has been producing at a reasonably steady rate of production.
Unless the calculated value of t
DA
exceeds the figure quoted for each geometrical
configuration then the well is not producing under semi-steady state conditions and the
Dietz shape factors cannot be used.
STABILIZED INFLOW EQUATIONS 146
60°
1
1
5
4
1
2
1
3
1
bounded reservoirs
3.45
3.43
3.45
In C
A
3.45
3.32
3.30
3.12
3.12
1.68
0.86
2.56
1.52
31.6
30.9
31.6
C
A
27.6
27.1
21.9
22.6
5.38
2.36
12.9
4.57
0.1
0.1
0.1
Stabilized
conditions
kt
µ
cA
for >
0.2
0.2
0.4
0.2
0.7
0.7
0.6
0.5
2.38
0.73
1.00
In C
A
-1.46
-2.16
1.14
-0.50
-2.20
-2.32
2.95
3.22
1.58
1.22
10.8
2.07
2.72
C
A
0.232
0.115
3.13
0.607
0.111
0.098
19.1
25
4.86
3.39
0.3
0.8
0.8
Stabilized
conditions
kt
µ
cA
for
>
2.5
3.0
0.3
1.0
1.2
0.9
0.1
0.1
1.0
0.6
1
2
1
2
1
1
2
4
1
4
1
4
2
1
43
In water-drive reservoirs
2
1
In reservoirs of unknown production character
1
2
Fig. 6.4 Dietz shape factors for various geometries
3
(Reproduced by courtesy of the
SPE of the AIME).
REFERENCES
1) Boburg, T.C. and Lantz, R.B., 1966. Calculation of the Production Rate of a
Thermally Stimulated Well. J.Pet.Tech., December: 1613−1623.
2) Craft, B.C. and Hawkins, M.F., Jr., 1959. Applied Petroleum Reservoir
Engineering. Prentice−Hall, Inc., Englewood Cliffs, New Jersey.

STABILIZED INFLOW EQUATIONS 147
3) Dietz, D.N., 1965. Determination of Average Reservoir Pressure from Build-Up
Surveys. J.Pet.Tech., August: 955−959.
CHAPTER 7
THE CONSTANT TERMINAL RATE SOLUTION OF THE RADIAL DIFFUSIVITY
EQUATION AND ITS APPLICATION TO OILWELL TESTING
7.1 INTRODUCTION
The constant terminal rate solution, which describes the pressure drop in the wellbore
due to constant rate production, is the basic equation used in well test analysis. Apart
from during the brief transient flow period, (infinite reservoir case) the solution depends
critically on the reservoir boundary condition. In this chapter the constant terminal rate
solution is presented for a well situated within a no-flow boundary for all the
geometrical configurations considered by Matthews, Brons and Hazebroek and for any
value of the flowing time. The solutions are expressed in dimensionless form to simplify
and generalise the mathematics. Superposition of such solutions leads to a general
well test equation which can be applied to the analysis of any pressure test conducted
in the wellbore. In this chapter such tests are described for reservoirs containing a fluid
of small and constant compressibility (undersaturated oil). In Chapter 8 the same
techniques are applied to well test analysis in gas and gas saturated oil reservoirs.
7.2 THE CONSTANT TERMINAL RATE SOLUTION
Starting from the static equilibrium pressure p
wf
= p
i
at t = 0, the constant terminal rate
solution of the radial diffusivity equation describes how the bottom hole flowing
pressure p
wf
varies as a function of time after imposing a rate change from 0 to q. This
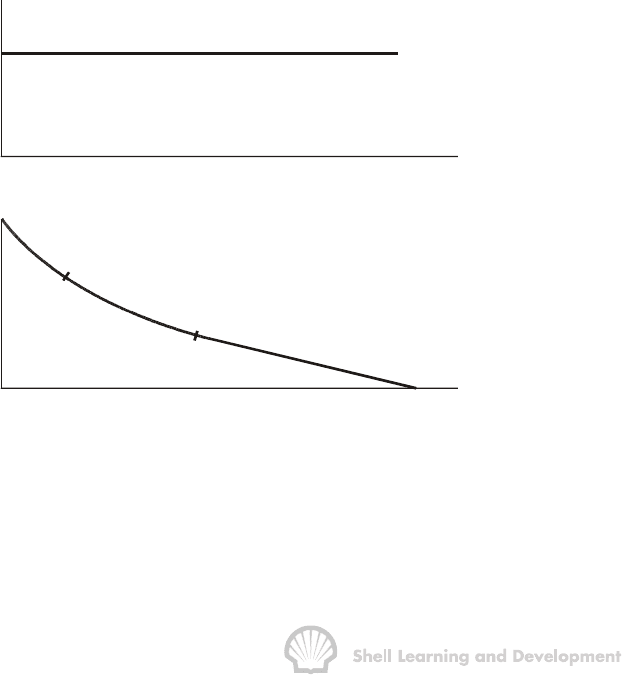
is illustrated in fig 7.1.
time
(b)
Pressure
p
wf
Transient
Late Transient
Semi Steady State
p
i
Rate
q
time
(a)
Fig. 7.1 Constant terminal rate solution; (a) constant production rate (b) resulting
decline in the bottom hole flowing pressure

OILWELL TESTING 149
The constant terminal rate solution is therefore the equation of p
wf
versus t for constant
rate production for any value of the flowing time. The pressure decline, fig. 7.1 (b), can
normally be divided into three sections depending on the value of the flowing time and
the geometry of the reservoir or part of the reservoir being drained by the well.
Initially, the pressure response can be described using a transient solution of the
diffusivity equation. It is assumed during this period that the pressure response at the
wellbore is not affected by the drainage boundary of the well and vice versa. This is
frequently referred to as the infinite reservoir case since, during the transient flow
period, the reservoir appears to be infinite in extent.
The transient phase is followed by the so-called late transient period during which the
influence of the drainage boundary begins to be felt. For a well producing from within a
no-flow boundary both the shape of the area drained and position of the well with
respect to the boundary are of major importance in determining the appropriate late
transient constant terminal rate solution.
Eventually, stabilised flow conditions will prevail which means that for the no-flow
boundary case the rate of change of wellbore pressure with respect to time is constant.
This corresponds to the semi-steady state condition described in Chapter 5, sec 3(b).
The constant terminal rate solution, for all values of the flowing time, was first
presented to the industry by Hurst and Van Everdingen in 1949. In their classic paper
on the subject
1
, the authors solved the radial diffusivity equation using the Laplace
transform for both the constant terminal rate and constant terminal pressure cases. The
latter, which is relevant to water influx calculations. will be described in Chapter 9.
The full Hurst and Van Everdingen solution, equ. 7.34, is a most intimidating
mathematical equation which contains as one of its components an infinite summation
of Bessel functions. The complexity is due to the wellbore pressure response during
the late transient period, since for transient and semi-steady state flow relatively simple
solutions can be obtained which will be described in sec. 7.3. The fact that the full
solution is so complex is rather unfortunate since the constant terminal rate solution of
the radial diffusivity equation can be regarded as the basic equation in wellbore
pressure analysis techniques. By superposition of such solutions, as will be shown in
sec. 7.5, the pressure response at the wellbore can be theoretically described for any
sequence of different rates acting for different periods of time, and this is the general
method employed in the analysis of any form of oil or gas well test.
7.3 THE CONSTANT TERMINAL RATE SOLUTION FOR TRANSIENT AND SEMI-
STEADY STATE FLOW CONDITIONS
During the initial transient flow period, it has been found that the constant terminal rate
solution of the radial diffusivity equation, determined using the Laplace transform, can
be approximated by the so-called line source solution which assumes that in
comparison to the apparently infinite reservoir the wellbore radius is negligible and the
wellbore itself can be treated as a line. This leads to a considerable simplification in the
OILWELL TESTING 150
mathematics and for this solution the boundary and initial conditions may be stated as
follows
i
i
r0
a) p p at t 0, for all r
b) p p at r , for all t
pq
c) lim r , for t 0
r2kh
µ
π
→
==
==∞
∂
=>
∂
(7.1)
Condition (a) is merely the initial condition that, before producing, the pressure
everywhere within the drainage volume is equal to the initial equilibrium pressure p
i
.
Condition (b) ensures the condition of transience, namely that the pressure at the
outer, infinite boundary is not affected by the pressure disturbance at the wellbore and
vice versa.
Condition (c) is the line source inner boundary condition.
In addition, the assumptions made in deriving the radial diffusivity equation in
Chapter 5 are retained. That is, that the formation is homogeneous and isotropic, and
drained by a fully penetrating well to ensure radial flow; the fluid itself must have a
constant viscosity and a small and constant compressibility. The solution obtained will,
therefore, be applicable to the flow of undersaturated oil. Having developed the simple
theory of pressure analysis based on these assumptions, many of the restrictions will
be removed by considering, for instance, the effects of partial well completion, the flow
of highly compressible fluids, etc. These modifications to the basic theory will be
gradually introduced in this and the following chapter.
Under the above conditions the diffusivity equation
1pcp
r
rr r k t
φµ
æö
∂∂ ∂
=
ç÷
∂∂ ∂
èø
(5.20)
can be solved by making use of Boltzmann's transformation
22
rcr
s
4 (Diffusivity constant)t 4kt
φµ
==
so that
scr
t2kt
φµ
∂
=
∂
(7.2)
and
2
2
scr
r
4kt
φµ
∂
=
∂
(7.3)
