Dake L.P. Fundamentals of reservoir engineering

Подождите немного. Документ загружается.

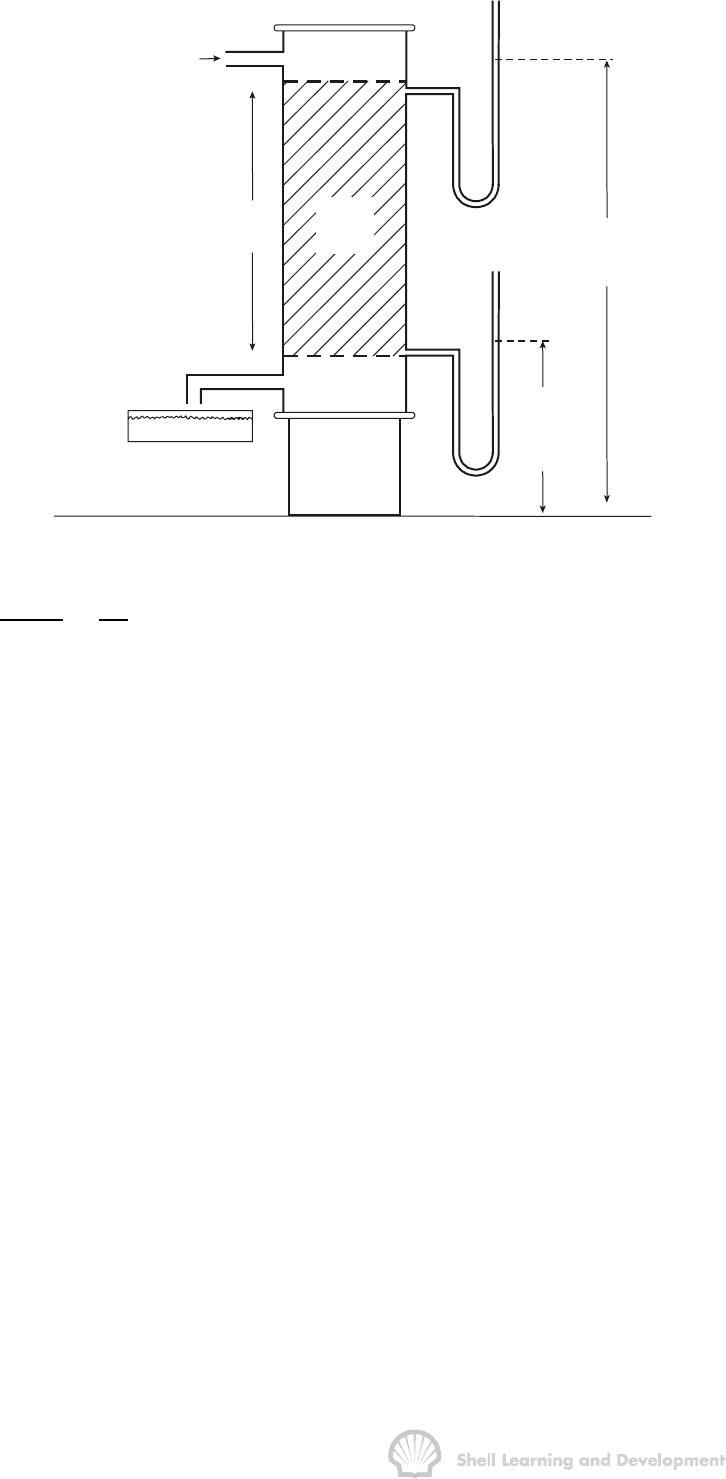
DARCY'S LAW AND APPLICATIONS 101

constant rate

water injection

q cc/sec

sand

pack

water collection

and measurement

mercury

manometers

Fig. 4.1 Schematic of Darcy's experimental equipment

hh h

uK K

−∆

(4.1)

where

u = flow velocity in cm/sec, which is the total measured flow rate q cc/sec,

divided by the cross-sectional area of the sand pack

∆h = difference in manometric levels, cm (water equivalent)

I = total length of the sand pack, cm, and

K = constant.

Darcy's only variation in this experiment was to change the type of sand pack, which

had the effect of altering the value of the constant K; otherwise, all the experiments

were carried out with water and therefore, the effects of fluid density and viscosity on

the flow law were not investigated. In addition the iron cylinder was always maintained

in the vertical position.

Subsequently, others repeated Darcy's experiment under less restrictive conditions,

and one of the first things they did was to orientate the sand pack at different angles

with respect to the vertical, as shown in fig. 4.2. It was found, however, that irrespective

of the orientation of the sand pack, the difference in height, ∆h, was always the same

for a given flow rate. Thus Darcy's experimental law proved to be independent of the

direction of flow in the earth's gravitational field.

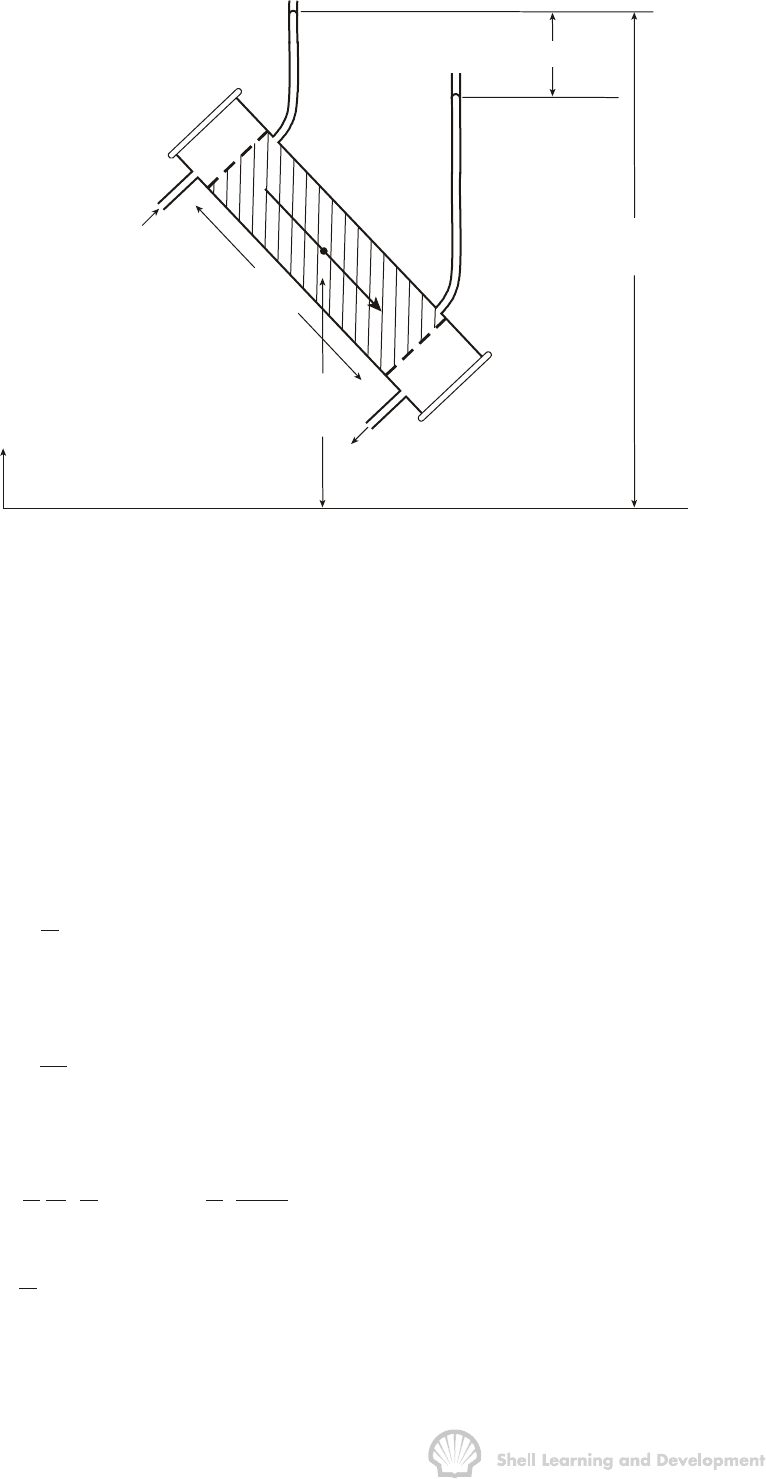
DARCY'S LAW AND APPLICATIONS 102

water

manometers

q cc / sec

+ z

∆h

datum plane; z = 0, p = 1 atm.

Fig. 4.2 Orientation of Darcy's apparatus with respect to the Earth's gravitational field

It is worthwhile considering the significance of the ∆h term appearing in Darcy's law.

The pressure at any point in the flow path, fig. 4.2, which has an elevation z, relative to

the datum plane, can be expressed in absolute units as

p =

g(h-z)

with respect to the prevailing atmospheric pressure. In this equation h is the liquid

elevation of the upper manometer, again, with respect to z = 0 and

is the liquid

(water) density. The equation can be alternatively expressed as

hg ( gz)

(4.2)

If equ. (4.1) is written in differential form as

= (4.3)

then differentiating equ. (4.2) and substituting in equ. (4.3) gives

Kd p K d(hg)

ugz

gdl g dl

æö

=+=

ç÷

èø

(4.4)

The term (

+ gz), in this latter equation, has the same units as hg which are:

distance × force per unit mass, that is, potential energy per unit mass. This fluid

potential is usually given the symbol Φ and defined as the work required, by a

DARCY'S LAW AND APPLICATIONS 103

frictionless process, to transport a unit mass of fluid from a state of atmospheric

pressure and zero elevation to the point in question, thus

1atm

−

Φ= +

(4.5)

Although defined in this way, fluid potentials are not always measured with respect to

atmospheric pressure and zero elevation, but rather, with respect to any arbitrary base

pressure and elevation (p

, z

) which modifies equ. (4.5) to

g(z z )

Φ= + −

(4.6)

The reason for this is that fluid flow between two points A and B is governed by the

difference in potential between the points, not the absolute potentials, i.e.

ABA

bbB

ppp

AB Ab Bb AB

ppp

dp dp dp

g(z z ) g(z z ) g(z z )

ρρρ

Φ−Φ= + − − + − = + −

òòò

It is therefore conventional, in reservoir engineering to select an arbitrary, convenient

datum plane, relative to the reservoir, and express all potentials with respect to this

plane. Furthermore, if it is assumed that the reservoir fluid is incompressible (

independent of pressure) then equ. (4.5) can be expressed as

Φ= +

(4.7)

which is precisely the term appearing in equ. (4.4). It can therefore be seen that the h

term in Darcy's equation is directly proportional to the difference in fluid potential

between the ends of the sand pack.

The constant K/g is only applicable for the flow of water, which was the liquid used

exclusively in Darcy's experiments. Experiments performed with a variety of different

liquids revealed that the law can be generalised as

(4.8)

in which the dependence of flow velocity on fluid density

and viscosity

is fairly

obvious. The new constant k has therefore been isolated as being solely dependent on

the nature of the sand and is described as the permeability. It is, in fact, the absolute

permeability of the sand, provided the latter is completely saturated with a fluid and,

because of the manner of derivation, will have the same value irrespective of the

nature of the fluid.

This latter statement is largely true, under normal reservoir pressures and flow

conditions, the exception being for certain circumstances encountered in real gas flow.

At very low pressures there is a slippage between the gas molecules and the walls of

DARCY'S LAW AND APPLICATIONS 104

each pore leading to an apparent increased permeability. This phenomenon, which is

called the Klinkenberg effect

, seldom enters reservoir engineering calculations but is

important in laboratory experiments in which, for convenience, rock permeabilities are

determined by measuring air flow rates through core plugs at pressures close to

atmospheric. This necessitates a correction to determine the absolute permeability

Due to its very low viscosity, the flow velocity of a real gas in a reservoir is much

greater than for oil or water. In a limited region around the wellbore, where the pressure

drawdown is high, the gas velocity can become so large that Darcy's law does not fully

describe the flow.

This phenomenon, and the manner of its quantification in flow

equations for gas, will be fully described in Chapter 8, sec. 6.

4.3 SIGN CONVENTION

Darcy's empirical law was described in the previous section without regard to sign

convention, it being assumed that all terms in equ. (4.8) were positive. This is adequate

if the law is being used independently to calculate flow rates; however, if equ. (4.8) is

used in conjunction with other mathematical equations then, just as described in

connection with the definition of thermodynamic compressibility in Chapter 1, sec. 4,

attention must be given to the matter of sign convention.

Linear flow

If distance is measured positive in the direction of flow, then the potential gradient dΦ/dl

must be negative in the same direction since fluids move from high to low potential.

Therefore, Darcy's law is

=−

(4.9)

Radial flow

If production from the reservoir into the well is taken as positive, which is the

convention adopted in this book, then, since the radius is measured as being positive in

the direction opposite to the flow, dΦ/dr is positive and Darcy's law may be stated as

(4.10)

4.4 UNITS: UNITS CONVERSION

In any absolute set of units Darcy's equation for linear flow is

(4.9)

in which the various parameters have the following dimensions

u = L/T;

= M/L

;

= M/LT; I = L and Φ (potential energy/unit mass) = L

. Therefore,

the following dimensional analysis performed on equ. (4.9):

DARCY'S LAW AND APPLICATIONS 105

[]

322

M/L L /T

TM/LTL

éùé ù

ëûë û

reveals that

[k] = [L

]

Thus the unit of permeability should be the cm

in cgs units, or the metre

in Sl units.

Both these units are impracticably large for the majority of reservoir rock, as will be

demonstrated in exercise 4.1, and therefore, a set of units was devised in which the

permeability would have a more convenient numerical size. These are the so-called

"Darcy units" (refer table 4.1) in which the unit of permeability is the Darcy. The latter

was defined from the statement of Darcy's law for horizontal, linear flow of an

incompressible fluid

kdp

=−

(4.11)

such that k = 1 Darcy when u = 1 cm/sec;

= 1 cp; and dp/dl = 1 atmosphere/cm.

Inspection of table 4.1 reveals that the units are a hybrid system based on the cgs

units. The only difference being that pressure is expressed in atmospheres, viscosity in

cp (centipoise) and, as a consequence, the permeability in Darcies. It was intended, in

defining this system of units, that not only would the unit of permeability have a

reasonable numerical value but also, equations expressed in these units would have

the same form as equations in absolute units. That is, there would be no awkward

constants involved in the equations other than multiples of π which reflect the geometry

of the system. Unfortunately, this latter expectation is not always fulfilled because the

Darcy, defined through the use of equ. (4.11), is based on an incomplete statement of

Darcy's law. Certainly, equ. (4.11) has the same form whether expressed in absolute or

Darcy units but considering the general statement of the flow law, equ. (4.9), applied to

an incompressible fluid (

≈ constant), then

DARCY'S LAW AND APPLICATIONS 106

Absolute units Hybrid units

Parameter Symbol Dimensions

cgs SI Darcy Field

Length I L cm metre cm ft

Mass M M gm kg gm lb

Time t T sec sec sec hr

Velocity u L/T cm/sec metre/sec cm/sec ft/sec

Rate q L

/T cc/sec metre

/sec cc/sec

Pressure p (ML/T

)/L

dyne/cm

Newton/meter

(Pascal) atm

stb/d(liquid)

Mscf / d (gas)

psia

Density

M/L

gm/cc kg/metre

gm/cc Ib/cu.ft

Viscosity

M/LT gm/cm.sec (Poise) kg/metre.sec cp cp

Permeability k L

metre

Darcy mD

TABLE 4.1

Absolute and hybrid systems of units used in Petroleum Engineering

DARCY'S LAW AND APPLICATIONS 107

kd kdp dz

dl dl dl

µµ

æö

==−+

ç÷

èø



(4.12)

in absolute units, while

kdp g dz

dl dl

1.0133 10

æö

=− +

ç÷

èø

(4.13)

in Darcy units. The constant 1.0133 × 10

is the number of dyne/cm

in one

atmosphere and is required because both

and g have the same units in both the cgs

and Darcy systems, and yet, the second term within the parenthesis of equ. (4.13)

must have the same units as the first, namely, atm/cm.

In spite of this obvious drawback, reservoir engineers tend to work theoretically using

equations expressed in Darcy units. This practice will generally be adhered to in this

text and, in the remaining chapters, the majority of the theoretical arguments will be

developed with equations expressed in these units.

When dealing with the more practical aspects of reservoir engineering, such as well

test analysis described in Chapters 7 and 8, it is conventional to switch to what are

called practical, or field units. The word practical is applied to such systems because all

the units employed are of a convenient magnitude. There are no rules governing field

units which therefore vary between countries and companies. The set of such units

presented in table 4.1 is, however, probably the most widely accepted in the industry at

the time of writing this book.

Because of the wide variation in unit systems employed by the industry, it is very

important that reservoir engineers should be adept at converting equations expressed

in Darcy units to the equivalent form in field units, or for that matter, any other set of

units. There is a systematic approach in making such conversions which, if rigorously

applied, will exclude the possibility of error. Consider, as an example, the conversion of

equ. (4.11) from Darcy to field units. Since

q = u(cm/sec) × A(cm

)

the equation can be expressed in more practical form, in Darcy units, as

k(D) A(cm ) dp

q(cc / sec) (atm / cm)

(cp) dl

=− (4.14)

which, when converted to field units will have the form

k(mD) A(ft ) dp

q(std / d) (constan t) (psi/ ft)

(cp) dl

=− (4.15)

in which the same symbols are used in both equations.

Making the conversion amounts to evaluating the constant in equ. (4.15) and this can

be achieved simply by remembering that equations must balance. Thus, if q in

DARCY'S LAW AND APPLICATIONS 108

equ. (4.14) is, say, 200 reservoir cc/sec, then the left hand side of equ. (4.15) must

also have the numerical value of 200, even though q in the latter is in stb/d, i.e.

conversion

q(stb / d) q(r.cc / sec)

factor

éù

×=

êú

ëû

which is satisfied by

r.cc / sec

q(stb / d) q(r.cc / sec)

stb / d

éù

êú

ëû

This preserves the balance on the left hand side of both equations. The conversion

factor can be expanded as

r.cc / sec r.cc / sec rb / d

stb/d rb/d stb/d

éùéùéù

êúêúêú

ëûëûëû

Applying this method throughout, then

and since

Dcm

atm

kmD Aft

mD ft

psi

stb r.cc / sec rb / d dp psi

d rb / d stb / d (cp) dl ft

D1cm atm1

; 30.48 and ; equ.(4.16)

mD 1000 ft psi 14.7

éù

êú

ëû

éùéù

ûëû

=− ×

êúêú

éù

ëûëû

êú

ëû

éù

éù éù

== =

êú

êú êú

ëû ëû

ëû

(4.16)

can be evaluated as

kA dp

q 1.127 10 (stb / d)

−

=− ×

(4.17)

EXERCISE 4.1 UNITS CONVERSION

1) What is the conversion factor between k, expressed in Darcies, and in cm

and metre

respectively.

2) Convert the full equation for the linear flow of an incompressible fluid, which in Darcy

units is

kA dp g dz

dl dl

1.0133 10

æö

=− +

ç÷

èø

to field units.

DARCY'S LAW AND APPLICATIONS 109

EXERCISE 4.1 SOLUTION

1) For linear, horizontal flow of an incompressible fluid

k(D) A(cm ) dp

q(cc / sec) (atm / cm) (Darcyunits)

(cp) dl

=−

and

22 2

k(cm ) A(cm ) dp (dyne / cm )

q(cc / sec) (Absolute cgs units)

(poise) dl (cm)

=−

The former equation can be converted from Darcy to cgs, absolute units by balancing

both sides of the resulting equation, as follows

atm

(dyne / cm )

k(cm ) A(cm )

dyne / cm

q(cc / sec)

dl (cm)

(poise)

poise

éù

êú

ëû ë û

=−

éù

êú

ëû

and evaluating the conversion factors

[]

k(cm ) A

dp 1

q (dyne / cm )

(poise) 100 dl 1.0133 10

éù

êú

ëû

=−

k(cm ) A

dp 1

1.0133 10

éù

êú

ëû

=−

But the numerical constant in this equation must be unity, therefore

1.0133 10

éù

=×

êú

ëû

so that 1 Darcy ≈ 10

-8

= 10

-12

metre

It is proposed that the industry will eventually convert to Sl (Système Internationale)

absolute units, (table 4.1), in which case the basic unit of permeability will be the

metre

. Because this is such an impracticably large unit, it has been tentatively

suggested

that a practical unit, the micrometre

(

), be "allowable" within the new

system. Since

= 10

-12

then

1 Darcy ≈ 1

DARCY'S LAW AND APPLICATIONS 110

It is also suggested that both the Darcy and milli-Darcy be retained as allowable terms.

2) For horizontal flow, the conversion from Darcy to field units of the first part of the flow

equation is

kA dp

q 1.127 10

Bdl

−

=− ×

(4.17)

To convert the gravity term, using the conventional manner described in the text, is

rather tedious but can be easily achieved in an intuitive manner. The second term,

(

g /1.0133×10

) dz/dl, must, upon conversion to field units, have the units psi/ft. The

only variable involved in this latter term is

, the fluid density. If this is expressed as a

specific gravity γ, then, since pure water has a pressure gradient of 0.4335 psi/ft, the

gravity term can be expressed as

0.4335γ

psi/ft

Furthermore, adopting the sign convention which will be used throughout this book,

that z is measured positively in the upward, vertical direction, fig. 4.2, and if

is the dip

angle of the reservoir measured counter-clockwise from the horizontal then

= sin

and the full equation, in field units, becomes

kA dp

q 1.127 10 0.4335 sin

Bdl

−

æö

=− × +

ç÷

èø

(4.18)

4.5 REAL GAS POTENTIAL

The fluid potential function was defined in section 4.2, in absolute units as

Φ= +

(4.6)

and for an incompressible fluid (

≈ constant) as

Φ= +

(4.7)

Liquids are generally considered to have a small compressibility but the same cannot

be said of a real gas and therefore, it is worthwhile investigating the application of the

potential function to the description of gas flow.

The density of a real gas can be expressed (in absolute units) as

ZRT

= (1.27)