Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

152

ИССЛЕДОВАНИЕ

УСТОЙЧИВОСТИ

СИСТЕМ

[ГЛ

Для

нее

нф

==0.

Обозначим

Составим характеристическое уравнение замкнутой системы:

G(p) =

Q(p)

+ P(p) =

+l)(T

p+l)(T

p+l)

или,

после раскрытия скобок,

(р)

О,

где

®2

+ fe.

Воспользуемся теперь условиями устойчивости (табл.

10 2,

стро-

ка

3).

Поскольку постоянные времени

коэффициент усиления

положительны,

то все

коэффициенты

#ь

#2,

положительны,

т.

е.

первое требование условий Гурвица выполняется Далее,

из

условия

Аг

> 0

следует

или,

после подстановки значений коэффициентов,

Г,Г

k)<

{Т{Г

Т,

Т,)(Т

(11.3)

Неравенство

(11.3)

можно преобразовать

виду

(у;

Т[)

{Т

тj)

(ПА

)

определяет

граничный

коэффициент

усиления

системы,

пре-

вышение которого ведет

неустойчивости. Граничный

коэффи-

циент

усиления

(11.4)

удобно представить

следующем виде:

Таким

образом, величина

зависит

не от

абсолютных значе-

ний

постоянных времени,

определяется только

их

отноше-

ниями.

При

равенстве

постоянных

времени,

гранич-

ный

коэффициент

усиления

принимает

минимально

воз-

можное

значение

= 8.

Граничный

коэффициент

усиления

гр

тем

больше,

чем

си/ьънее

отличаются

друг

от

друга

постоянные

времени

ИССЛЕДОВАНИЕ

УСТОЙЧИВОСТИ ТИПОВЫХ

СИСТЕМ

IS3

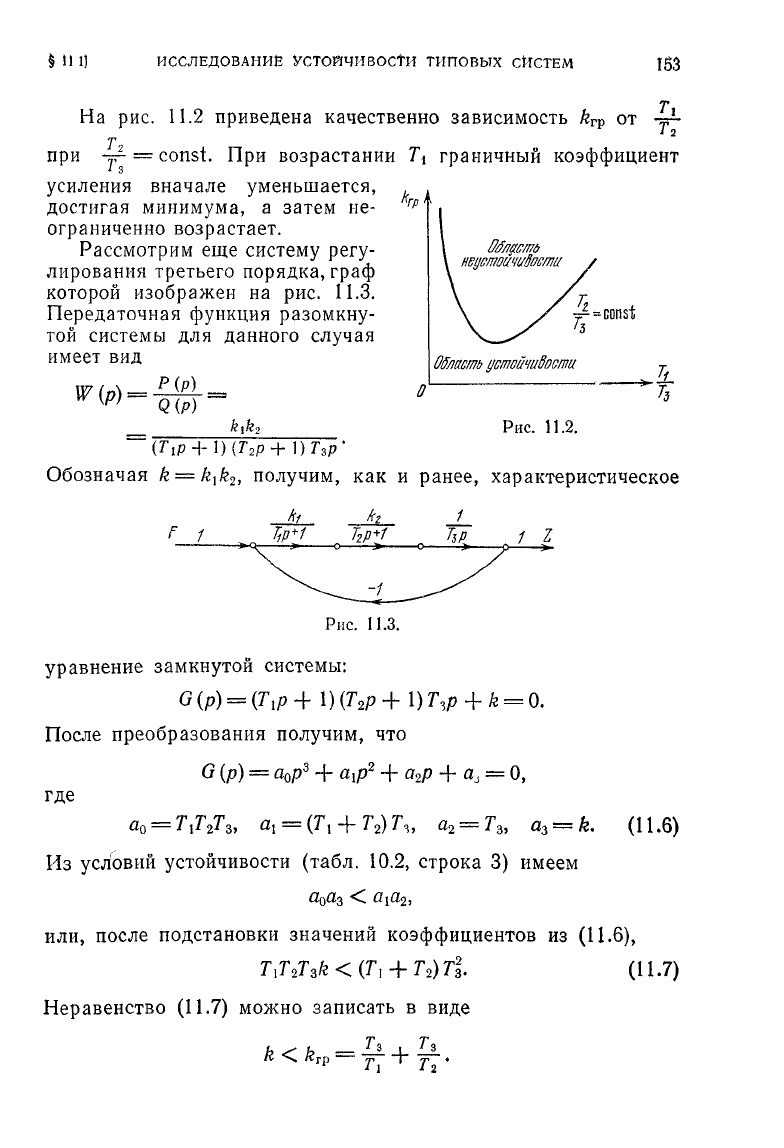
На

рис.

11.2

приведена качественно зависимость

от

при

у-=

const. При возрастании

граничный коэффициент

усиления вначале уменьшается,

достигая минимума, а затем не-

ограниченно возрастает.

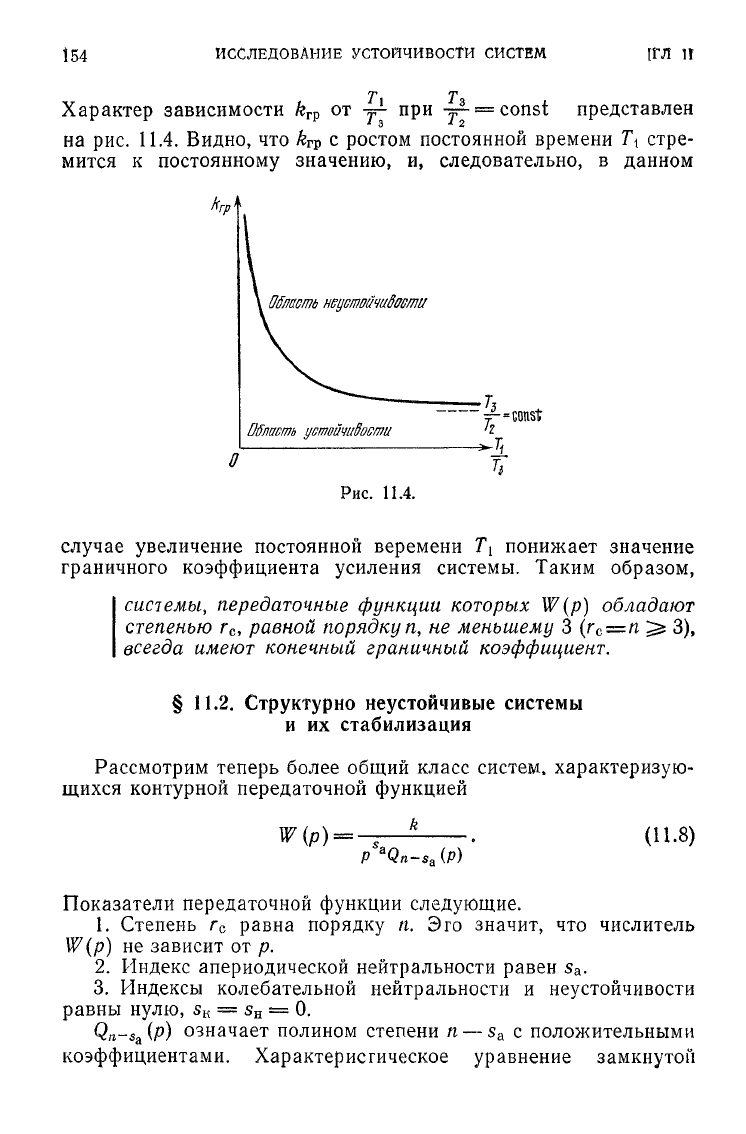
Рассмотрим еще систему

регу-

лирования третьего порядка, граф

которой изображен на рис. 11.3.

Передаточная функция разомкну-

той системы для данного случая

имеет вид

/„\

(Р)

Q(P)

Область

устошбооти

Рис.

11.2.

Обозначая

получим, как и ранее, характеристическое

уравнение замкнутой системы:

G (р) =

{Т

(Т

+l)Ttf

= 0.

После преобразования получим, что

(/?)

{

а,

= 0,

где

ао

ВДГд,

(7-,

^)^,

(11.6)

Из

условий устойчивости (табл. 10.2, строка 3) имеем

CIQCLS

&\CL

)

или,

после подстановки значений коэффициентов из (11.6),

/г

)

з.

(11.7)

Неравенство

(11.7)

можно записать в виде

ь^

—II.JL.LL

154

ИССЛЕДОВАНИЕ

УСТОЙЧИВОСТИ СИСТЕМ

ГГЛ

т т

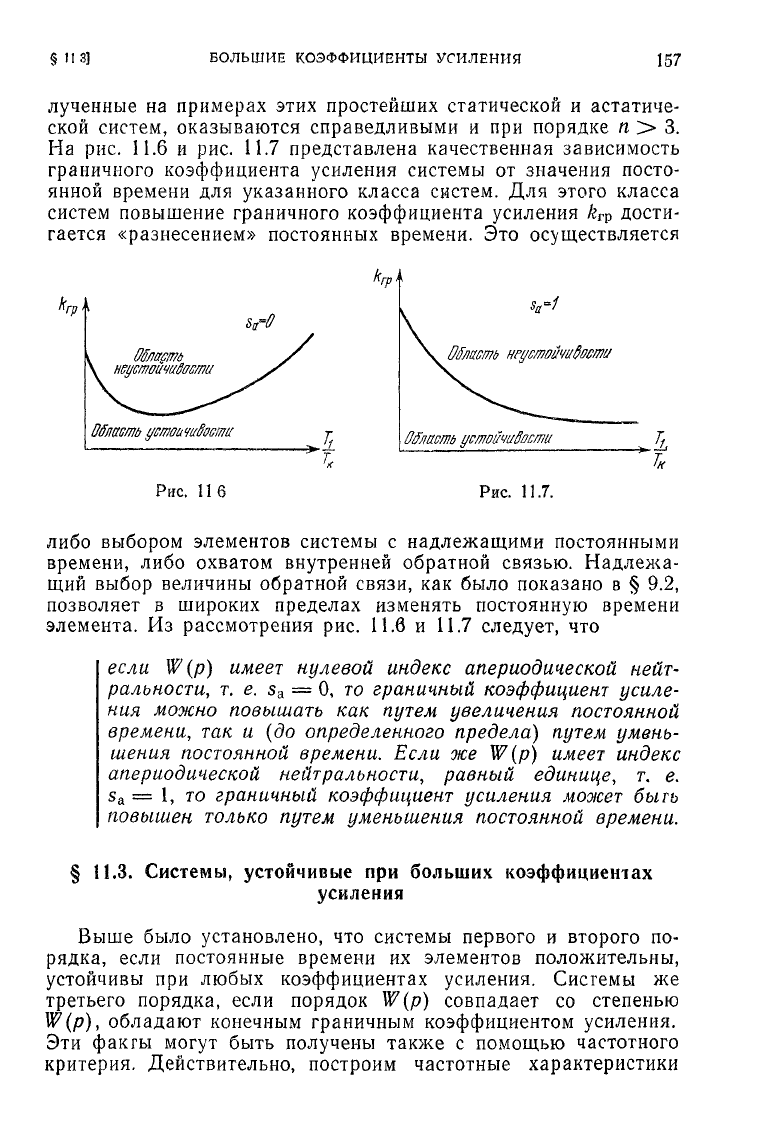
Характер зависимости

от -^

const представлен

на

рис.

11.4.

Видно, что

с ростом постоянной времени

стре-

мится

к постоянному значению, и, следовательно, в данном

Область

ниустпачи8ос/ли

Рис.

11.4.

случае

увеличение постоянной веремени Т\ понижает значение

граничного коэффициента усиления системы. Таким образом,

системы,

передаточные

функции

которых

(р)

обладают

степенью

равной

порядку

/г,

не

меньшему

(г

=п

^ 3),

всегда

имеют

конечный

граничный

коэффициент.

11.2.

Структурно неустойчивые системы

их стабилизация

Рассмотрим теперь более общий класс систем, характеризую-

щихся контурной передаточной функцией

Qn-

(Р)

(11.8)

Показатели

передаточной функции следующие.

1. Степень

равна порядку п.

Эго

значит, что числитель

W(p)

не зависит от р.

2. Индекс апериодической нейтральности равен

3. Индексы колебательной нейтральности и неустойчивости

равны

нулю,

Qn-s^ip)

означает полином степени п —

с положительными

коэффициентами.

Характеристическое уравнение замкнутой

Т12]

СТРУКТУРНО

НЕУСТОЙЧИВЫЕ

СИСТЕМЫ

155

системы в этом случае

будет

иметь вид

или,

в развернутой форме,

... +

р'"

+ *

(11.9)

где

> 0,

> 0, ...,

> 0.

При

^ 2 часть коэффициентов характеристического уравнения

(11.9),

а именно

-ь

#п-2,

...,

Sa+1

обращается в нуль, и, сле-

довательно, не

будет

выполнено условие положительности всех

коэффициентов,

что свидетельствует о неустойчивости системы.

Никаким

выбором

...,

и k при

^ 2 невозможно

придать системе устойчивость, т. е. стабилизировать ее. Итак,

системы,

для

которых

степень

передаточной

функции

W(p)

равна

ее

порядку,

структурно

неустойчивы,

если

ин-

декс

апериодической

нейтральности

не

меньше

двух.

Та-

кие

системы

содержат

не

менее

двух

последовательно

со-

единенных

интеграторов.

Для стабилизации структурно неустойчивых систем необхо-

димо изменить их структуру таким образом, чтобы уменьшить

степень передаточной функции. Действительно, если изменить

структуру системы таким образом, чтобы передаточная функция

W(р)

приняла вид

*Qn-s

(Р)

то степень передаточной функции

будет

равна

— п —

т,

где

— степень полинома Р{р).

Если

индекс неминимально-фазовости равен нулю,

cf>

= 0, то мож-

но

подобрать коэффициенты Р(р) так, чтобы характеристи-

ческое уравнение замкнутой системы

имело все коэффициенты, отличные от нуля. Для этого, очевид-

но,

нужно, чтобы степень многочлена Р(р) была не меньше

—1.

Итак,

условие, при котором система перестает быть струк-

турно неустойчивой, можно записать в виде

—

156

ИССЛЕДОВАНИЕ

УСТОЙЧИВОСТИ

CIICTLM

[ТЛ

1Г

Стабилизация

структурно

неустойчивой

системы

достига-

ется

введением

внутренней

связи,

охватывающей

один

из

интеграторов,

либо

введением

производной.

Такого рода коррекцию системы можно также рассматривать

как

параллельную коррекцию.

структурно неустойчивым системам относятся также систе-

мы,

для которых степень передаточной функции

W(p)

равна ее

порядку и если индекс неустойчивости

не меньше

двух,

т. е.

если, например,

(г,р

—

(г

—

(р)

•

где

Т\

> 0. Характеристическое уравнение замкнутой си-

стемы имеет вид

Построим

зависимость G(p) при изменении р от 0 до

оо.

По-

скольку при

7р~

ир =

1 / 2

имеем

G(y-)

—

то эта зависимость имеет вид,

показанный

на рис.

11.5.

G(p)

с ростом р изменяется не моно-

тонно.

Это возможно лишь то-

гда, когда не все коэффициен-

ты характеристического урав-

Рис.

11.6.

нения

G(/?)=0

(11.10) поло-

жительны. Следовательно, ха-

рактеристический многочлен G(p) имеет по крайней мере один

отрицательный коэффициент при любых значениях параметров

системы.

Система,

которой

степень

передаточной

функции

W(p)

равна

ее

порядку,

индекс

неустойчивости

^ 2, струк-

турно

неустойчива.

Такую

структурно

неустойчивую

си-

стему

можно

стабилизировать

введением

внутренней

об-

ратной

связи,

охватывающей

неустойчивый

элемент.

При

индексе апериодической нейтральности

или

=l,

если индексы колебательной нейтральности

и неустойчиво-

сти

равны нулю и все полюсы W(p) вещественны (а значит, и

отрицательны), мы при п = 3 приходим к рассмотренным выше

простейшим статической и астатической системам. Выводы, по-

ИЗ]

БОЛЬШИЕ

КОЭФФИЦИЕНТЫ

УСИЛЕНИЯ

157

лученные на примерах этих простейших статической и астатиче-

ской

систем, оказываются справедливыми и при порядке п

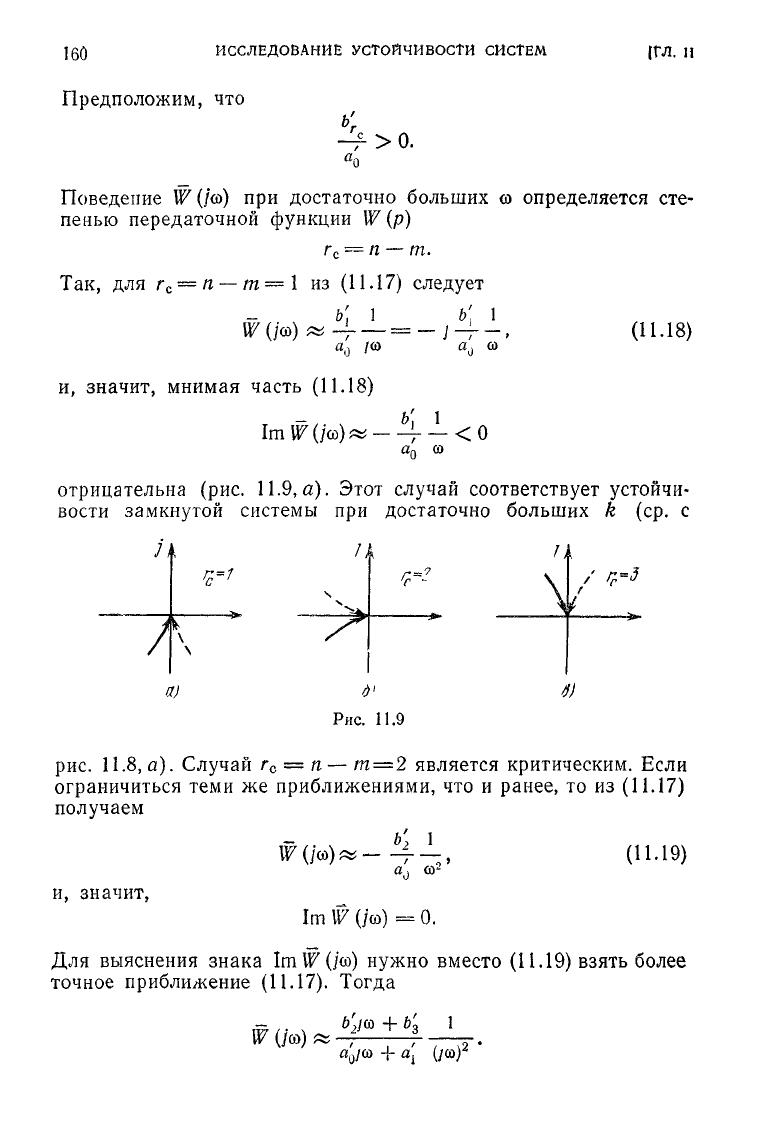
На

рис.

11.6

и рис.

11.7

представлена качественная зависимость

граничного коэффициента усиления системы от значения посто-

янной

времени для указанного класса систем. Для этого класса

систем повышение граничного коэффициента усиления

Уг

гр

дости-

гается «разнесением» постоянных времени. Это осуществляется

класть

уе/лойчиНости

Рис,

Рис.

11.7.

либо выборОхМ элементов системы с надлежащими постоянными

времени,

либо охватом внутренней обратной связью. Надлежа-

щий

выбор величины обратной связи, как было показано в § 9.2,

позволяет в широких пределах изменять постоянную времени

элемента. Из рассмотрения рис.

11.6

11.7

следует, что

если

W(p)

имеет

нулевой

индекс

апериодической

нейт-

ральности,

т. е.

= 0, то

граничный

коэффициент

усиле-

ния

можно

повышать

как путем увеличения

постоянной

времени,

так и (до

определенного

предела)

путем

умень-

шения

постоянной

времени.

Если же

W(p)

имеет

индекс

апериодической

нейтральности,

равный

единице,

т.

е.

1, то

граничный

коэффициент

усиления

может

быть

повышен

только

путем

уменьшения

постоянной

времени.

11.3. Системы, устойчивые при больших коэффициентах

усиления

Выше было установлено, что системы первого и второго по-

рядка, если постоянные времени их элементов положительны,

устойчивы при любых коэффициентах усиления. Системы же

третьего порядка, если порядок

W(p)

совпадает со степенью

W(p),

обладают конечным граничным коэффициентом усиления.

Эти факты могут быть получены также с помощью частотного

критерия.

Действительно, построим частотные характеристики

158

ИССЛЕДОВАНИЕ

УСТОЙЧИВОСТИ

СИСТЕМ

разомкнутых систем

-7W

+ -

—

ГЖ

Г)/ш+

[ГЛ.

1Г

(11.11)

(11.12)

(11.13)

При

малых со

при больших со частотные характеристики разо-

мкнутых систем приближенно равны

\У{ш)&-}-у^,

(11.11')

(11.120

(П.130

Поэтому нетрудно изобразить качественно соответствующий вид

частотных характеристик. На рис.

11.8

изображены нормирован-

ные

частотные характеристики

Жирными

линиями отмечены участки нормированных частотных

характеристик, соответствующие приближенным значениям

W(jco)

(11.11

)

—

(11.13

При возрастании

точка

Г—г-,

/0J

движет-

ся

вдоль действительной оси

началу координат. При этом для

систем первого

второго порядка точка

(—

-т-,

/0J

ни

при ка-

ком

значении

k не

будет

охватываться частотными характери-

стиками

(/со) (рис.

11.8,

а, б),

для

систехмы

третьего порядка,

начиная

некоторого значения, точка

Г—

у,

/Отстанет

охваты-

П.Si

БОЛЬШИЕ

КОЭФФИЦИЕНТЫ

УСИЛЕНИЯ 159

ваться частотной характеристикой (рис.

11.8,

в), что свидетель-

ствует

об устойчивости систем первого и второго порядка при

любом

и о наступлении неустойчивости в системах третьего

порядка

при превышении k некоторого граничного значения. Эти

элементарные соображения

будут

положены в основу определе-

ния

условий, при которых замкнутая система произвольного по-

рядка допускает теоретически неограниченное увеличение

коэф-

фициента

усиления без нарушения ее устойчивости.

Рассмотрим передаточную функцию

где

Q(p)

<&«+a\p«-i+

... +

представляет собой нормированную передаточную функцию

разомкнутой системы. Характеристическое уравнение замкнутой

системы запишется в виде

или

lQ(/?)

P(p)

(11.15)

При

===

со это характеристическое уравнение вырождается в

предельное

уравнение

Р(р)

(11.16)

Поскольку

при

= оо система должна быть устойчива, то

корни,

этого предельного уравнения должны быть

^евыми.

Отсюда

сле-

дует,

что индекс неминимально-фазовости

W(p)

(11.14)

должен

быть равен нулю, т. е.

нф

= 0.

Но,

чтобы замкнутая система была устойчива при достаточно

больших k, поведение нормированной частотной характеристики

И?(/со)

при больших значениях k должно быть гюдобным

поведе-

нию

нормированных частотных характеристик

W(j(d)

систем

пер*

вого и второго порядка (рис. 11.8,

а,

б). Подставляя в

(11.14)

= /со и ограничиваясь при достаточно больших со старшими

степенями

со, получим

150

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМ

Предположим, что

{ГЛ.

Поведение W (/со) при достаточно больших со определяется сте-

пенью передаточной функции

W(р)

(11.18)

Так,

для t

и,

значит,

= п — т = 1

/со

мнимая

часть

Imtf

ИЗ

—

т.

(11.17)

следует

Ь\

/со

1.18)

в)«

—

со

отрицательна (рис.

11.9,

а). Этот случай соответствует

устойчи-

вости замкнутой системы при достаточно больших k (ср. с

Рис.

11.9

рис.

11.8, а). Случай

п—

т=2

является критическим. Если

ограничиться теми же приближениями, что и ранее, то из

(11.17)

получаем

Ъ'

(/со)

я^

—,

(11.19)

и,

значит,

(/со)

Для выяснения знака

ImW(/co)

нужно вместо

(11.19)

взять более

точное приближение

(11.17).

Тогда

(/со)

Ь'

]а>

ф/со

а\

(/со)

|113]

БОЛЬШИЕ

КОЭФФИЦИЕНТЫ

УСИЛЕНИЙ

1б1

И,

значит,

Q l

Замкнутая система

будет

устойчива при достаточно большом

если мнимая часть

tF(/co)

будет

отрицательна (рис.

11.9,6),

или

|д!

__ . _ __ _ . _

ао/сэ

а!

со

~\-а\

т. е. если выполняется неравенство

—

6з<^о

> 0,

что эквивалентно,

ь' ь'

-4>-f.

(П-20)

Это условие обеспечивает поведение

W(/со)

при достаточно боль-

ших со, аналогичное изображенному на рис.

11.8,6.

Если же

= п — т = 3, то из

(11.17)

получаем

Ьо

&о

(/со)

«-4—з-

/-гт,

(П.21)

(/со)

и,

значит, мнимая часть (11.21)

положительна (рис.

11.9,

б). Этот случай соответствует неустой-

чивости замкнутой системы при достаточно больших

так как

при

малых частотах мнимая часть отрицательна и, значит, рано

или

поздно,

W(/со)

с ростом со пересечет отрицательную действи-

тельную ось (ср. с рис.

11.8,

в) Аналогичная картина

будет

иметь место и при

n — m = 2 и невыполнении неравенства

(11.20) (см. рис.

11.8,6).

Теперь можно подвести итог проведенному анализу и прийти

следующему заключению.

Замкнутая

система

будет

устойчива

при

достаточно

боль-

ших

коэффициентах

усиления,

если

индекс

неминимально-

фазовости

W (р)

равен

нулю,

нф

= 0, и при

= 1 вы-

Ь\

полнено

условие

— > 0, при

= 2

выполнено

условие

—г

> — •

При

> 2 или при

0 замкнутая

система

не

может

быть

устойчивой

при

достаточно

больших

коэф-

фициентах

усиления,

Я 3

Цнпкин