Cooper L.N., Feldman D. (Eds.) BCS: 50 Years

Подождите немного. Документ загружается.

October 4, 2010 10:17 World Scientiﬁc Review Volume - 9.75in x 6.5in ch20

BCS from Nuclei and Neutron Stars to Quark Matter and Cold Atoms 511

systems of the Meissner eﬀect in superconductors.

The detailed theory

was soon worked out by Beliaev,

who came to Copenhagen for a year at

the end of 1957, and by Migdal.

As Beliaev showed, the moment of inertia

is given by

I = 2

ν,ν

hν

|νi|

+ E

− v

, (1)

where the u and v, the usual BCS coherence factors associated with the single

particle levels ν and ν

, are responsible for the reduction of the moment of

inertia from its classical value, similar to the reduction of the normal electron

fraction in BCS. Explicit calculations by Migdal and others later gave good

agreement with experiment.

3. Neutron Stars

Migdal, in the introduction to his paper on superﬂuidity and moments of

inertia of nuclei,

makes the prescient remark that “superﬂuidity of nuclear

matter may lead to some interesting cosmological phenomena if stars exist

which have neutron cores. A star of this type would be in a superﬂuid state

with a transition temperature corresponding to 1 MeV.” The theme of super-

ﬂuidity of nuclear matter in neutron stars was later ampliﬁed by Ginzburg

and Kirzhnits,

prior to the discovery of pulsars and their identiﬁcation as

rotating neutron stars, and by Ruderman,

and Baym, Pethick and Pines,

among others.

Figure 1 shows the cross-section of a neutron star. With increasing depth

in the star, the matter becomes more and more neutron rich as the electron

Fermi energy rises; electron captures, e + p → n + ν

, convert protons into

neutrons in the formation of the neutron star (the produced neutrino es-

capes). At the “neutron drip” point, the ﬁrst solid line in the crust in Fig. 1,

the matter become so neutron rich that the bound neutron states are ﬁlled

and the continuum neutron states begin to ﬁll; the still solid matter becomes

permeated by a sea of free neutrons in addition to the sea of electrons. Above

the neutron-drip point, the protons remain localized in nuclei in shells with Z

= 40 or 50 as the matter continues to become more and more neutron rich,

until the “pasta nuclei” regime, where the nuclear shapes becomes highly

distorted. The neutron ﬂuid is expected to be superﬂuid, with BCS pairing

in the crust in

and pairing in

states in the liquid core. The proton

ﬂuid in the interior is expected to be a Type II superconductor paired in

states.

October 4, 2010 10:17 World Scientiﬁc Review Volume - 9.75in x 6.5in ch20

512 G. Baym

Nuclei and electrons

Nuclei, electrons and free neutrons

Pasta nuclei

OUTER CORE

Free neutrons, protons and electrons

INNER CORE

hyperons

meson condensates

quark droplets

quark-gluon plasma

CRUST

~10km

neutron

pairing in

crust

proton

pairing in

core

neutron

Fig. 1. Cross-section of a neutron star. The neutron superﬂuid in the crust is

expected to be paired in

states, as is the proton superﬂuid in the core. The

neutron superﬂuid in the core is expected to be paired in

states. The electrons

are normal, however. A quark ﬂuid in the core is also expected to be BCS paired

states.

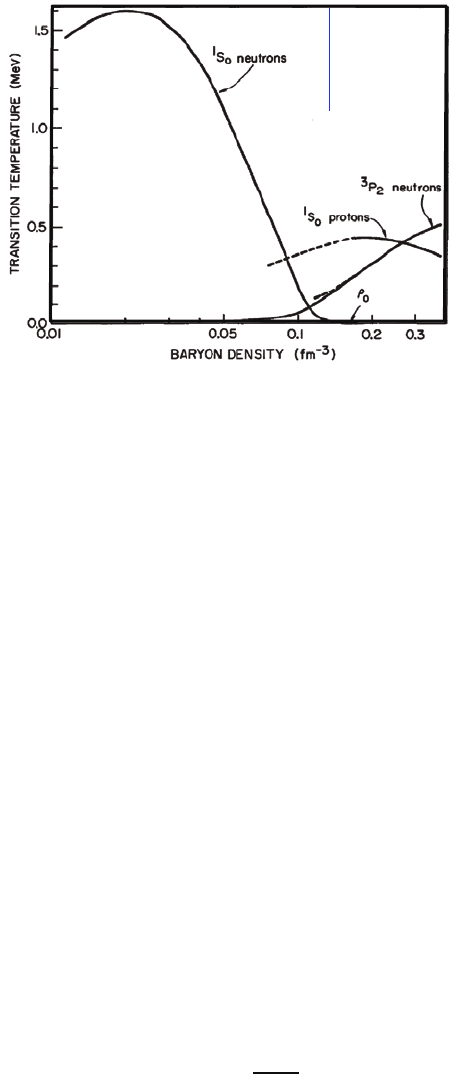
The original estimates of pairing gaps were based on nucleon–nucleon

scattering phase shifts, e.g. by Ref. 18 for neutrons, and by Ref. 19 for

protons. The corresponding transition temperatures for pairing are illus-

trated in Fig. 2. Over the years, more and more sophisticated calculations

of nucleonic pairing, taking into account dynamical screening of the eﬀective

interactions between nucleons, have been performed. More recently, numer-

ical simulations of dense nuclear matter via Monte Carlo have been carried

out to determine pairing gaps; various calculations are reviewed in Ref. 21.

Figure 3 shows the results of a quantum Monte-Carlo (QMC) calculation

by Gezerlis and Carlson for the zero temperature BCS pairing gap in low

density pure neutron matter (as found in the crust of a neutron star); the

calculation has been done for 66 to 68 particles in a box with an s-wave

nucleon–nucleon potential with scattering length a = −18.5 fm and an ef-

fective range r

= 2.7 fm.

–

For comparison, the plot also shows the BCS

mean-ﬁeld gap for the same s-wave scattering length.

October 4, 2010 10:17 World Scientiﬁc Review Volume - 9.75in x 6.5in ch20

BCS from Nuclei and Neutron Stars to Quark Matter and Cold Atoms 513

CORECRUST

Fig. 2. Estimates of transition temperature for nucleonic pairing, based on

nucleon–nucleon phase shifts.

The highly relativistic electrons, one should note, are too weakly inter-

acting to undergo BCS pairing at ambient neutron star temperatures; the

transition temperature for electron superconductivity would be ∼ µ

−1/α

where α = e

/~c is the electromagnetic ﬁne structure constant and µ

is the

electron chemical potential.

BCS pairing in neutron stars leads to macroscopic behavior familiar

in laboratory superﬂuids and superconductors. In a rotating neutron

starneutron star, the neutron superﬂuid rotates by forming vortex lines par-

allel to the rotation axis, around which the superﬂuid circulation is quantized

in units of κ = π~/2m

, where m

is the neutron mass. The proton ﬂuid, on

the other hand, is threaded by a triangular (Abrikosov) array of magnetic

ﬂux tubes each carrying a ﬂux quantum, φ

= π~c/e, parallel to the mag-

netic ﬁeld, as in a Type II superconductor. Even though ambient magnetic

ﬁelds are below the critical magnetic ﬁeld for ﬂux expulsion, the enormous

electrical conductivity of the normal state implies that the characteristic

times for ﬂux diﬀusion from macroscopic regions, of order R

τ, where R

is the neutron star radius and τ is the microscopic scattering time, are typi-

cally comparable with the age of the universe.

23,24

Proton superconductivity

forms in the magnetic ﬁeld present at the birth of the neutron star, despite

the Meissner eﬀect.

While the vortex cores are of order 10 fm in radius, the characteris-

tic spacing of neutron vortices ' 0.01

P (s) cm (where P (s) is the pulsar

October 4, 2010 10:17 World Scientiﬁc Review Volume - 9.75in x 6.5in ch20

514 G. Baym

Fig. 3. Superﬂuid pairing gap for low density neutron matter, as a function of

the neutron Fermi momentum, k

calculated by QMC and compared with the

mean-ﬁeld BCS gap. The ﬁgure also shows the equivalent result for pairing of cold

atomic fermions, where the eﬀective range is negligible, and the unitarity limit of

the QMC calculation (right arrow) compared with experiment (left arrow). Figure

from Gezerlis’s thesis.

rotational period in seconds) is macroscopic. The proton vortices, on the

other hand, are separated by sub-

Angstrom scales owing to the enormous

magnetic ﬁelds (B ∼ 10

G) in typical neutron stars.

The phenomenon of pulsar glitches, or sudden rotational speed-ups, pro-

vides an unusual opportunity to probe the superﬂuidity of neutron star

matter. Over 90 glitches have been observed in over 30 pulsars. Since its

discovery in 1968, the Vela pulsar PSR 0833-45, with a period 0.089 ms,

has undergone some 15 such sudden increases of its rotation rate Ω, of

size ∆Ω/Ω ∼ 10

−6

, corresponding to an increase in rotational energy,

∆E

rot

= IΩ∆Ω ∼ 10

erg, where I ∼ 10

g cm

is the stellar moment

of inertia. The Crab pulsar, since its discovery in 1969, has undergone some

14 glitches of average size ∆Ω/Ω ∼ 10

−8

− 10

−9

. After a speed-up, the

rotation relaxes back to its preglitch behavior over days to years.

A pulsar glitch, involving an energy comparable to the entire energy of

the pulsar magnetosphere but with little change in the electromagnetic pul-

sations, appears to originate within the neutron star. On the one hand, re-

laxation processes within a normal star are microscopically rapid,

strongly

suggesting that the long relaxation times observed in glitches are related to

October 4, 2010 10:17 World Scientiﬁc Review Volume - 9.75in x 6.5in ch20

BCS from Nuclei and Neutron Stars to Quark Matter and Cold Atoms 515

superﬂuidity. As reviewed in Ref. 26, the most likely mechanism involves

pinning of superﬂuid neutron vortices to the nuclei in the inner crust and

their slow outward creep through the nuclear lattice.

Since the angular mo-

mentum of a vortex, ∼N~(1 −r

) (where N is the number of particles

in the superﬂuid, r is the radial position of the vortex in polar coordinates,

and R is the stellar radius) decreases as the vortex moves outwards, the

spin-down of a neutron star is controlled by the rate at which vortices can

move radially under dissipation. To the extent that vortices remain ﬁxed to

the crystal lattice, the superﬂuid angular velocity remains constant, allowing

the diﬀerence between the angular velocities of the superﬂuid and the solid

crust to grow as the crust slows. This diﬀerential motion can then act as the

source of energy that powers glitches, with sudden transfers of angular mo-

mentum from the superﬂuid to the crust caused by catastrophic unpinning

of many vortex lines, or by cracking of the crust to which the vortex lines

are pinned. An unpinned line experiences a frictional force which transfers

angular momentum to the crust on minute time scales. Following eventual

repinning the vortices resume their slow outward creep, with the long-term

observed post-glitch relaxation reﬂecting variations in the creep rate.

4. Pairing in Quark Matter

With increasing density in a neutron star, the nucleons, composed of three

valence quarks, are squeezed together and the liquid becomes dominated by

quark degrees of freedom, eventually becoming “quark matter.” The compo-

nents of quark matter are the very light up (u) and down (d) ﬂavor quarks;

at higher densities more massive strange (s) quarks enter as the chemical

potential of d quarks exceeds the strange quark mass, ∼100 MeV, plus

interaction corrections. At non-zero temperature gluons are also present.

Understanding the transition to quark matter remains an important theo-

retical challenge. The transition is most likely gradual; indeed once nucleons

overlap considerably, the matter should percolate, opening the possibility of

their quark constituents propagating throughout the system.

Quark matter at low temperatures becomes a color superconductor,

driven (at very high densities) by exchange of gluons.

28,29

Two

pair-

ing states, with condensates antisymmetric in color (which takes on three

values, nominally red, blue, and green) and ﬂavor are most energetically fa-

vorable: a two-ﬂavor color-antitriplet 2SC or isoscalar state, in which only

u and d quarks are paired; and for massless u, d and s quarks, a color-ﬂavor

locked (CFL) state

that breaks both color and ﬂavor symmetry, containing

October 4, 2010 10:17 World Scientiﬁc Review Volume - 9.75in x 6.5in ch20

516 G. Baym

18 condensates, e.g. pairing of a red u quark with a blue s quark, a blue s

quark with a green d quark, and a green d quark with a red u quark, etc. The

CFL state is the most stable for three ﬂavors of massless quarks in the weak

coupling limit, both at zero temperature, and near the critical temperature

Quark pairing would play a role in the dynamics of neutron stars. The

2SC and CFL phases respond quite diﬀerently to magnetic ﬁelds and ro-

tation.

The isoscalar state, if a Type II superconductor, would behave

analogously to that of superconducting protons in a neutron star, forming

magnetic vortices in response to ordinary magnetic ﬁeld with ﬂux quantum

6π~c/

+ e

, where g is the qcd coupling constant and e the electron

charge. As in a rotating superconductor, this state responds to rotation by

forming a very weak London magnetic ﬁeld, B

∼

1 G (the ﬁeld is actu-

ally a superposition of electromagnetic and color-gluon magnetic ﬁelds; the

latter dominates).

On the other hand, the CFL phase forms U(1) vortices in response to

rotation, as do superﬂuid neutrons, with a quantum of circulation, 3π~c

/µ,

where µ is the baryon chemical potential.

Such vortices could play a role

in the pinning and depinning of rotational vortices that give rise to pulsar

glitches.

Vortices involving only an electromagnetic U(1) phase of the gap

are unstable

; however, the system does support stable magnetic vortices

which involve the gradients of the full SU(3)

× U(1)

color structure.

As with superconducting protons in neutron stars, magnetic ﬁelds in color

superconducting matter would be frozen in an intermediate state composed

of alternating regions of normal and superconducting material if the sys-

tem is a Type I superconductor, or in a lattice of vortices if a Type II

superconductor.

5. Coupling of Pairing and Chiral Symmetry

The rich structure of quark matter opens new physics of superconductivity.

A basic symmetry of the strong interaction is chiral symmetry, the conser-

vation of the handedness or helicity (the spin of a particle along its direction

of momentum) of massless quarks. Chiral symmetry is spontaneously bro-

ken in the normal vacuum, giving rise to a quark-antiquark condensate h¯qqi;

such a condensate is an analog of magnetization in condensed matter sys-

tems. Figure 4 shows a possible schematic phase diagram of dense matter in

the temperature — baryon chemical potential µ plane. At low temperatures

and densities, matter is in the hadronic phase whose degrees of freedom are

October 4, 2010 10:17 World Scientiﬁc Review Volume - 9.75in x 6.5in ch20

BCS from Nuclei and Neutron Stars to Quark Matter and Cold Atoms 517

hadrons

deconned

quarks and gluons

color

superconductor

baryon chemical potential

temperature

<qq>=0

Fig. 4. Schematic phase diagram of high density quark matter. In the hadronic

regime, chiral symmetry is spontaneously broken, with a non-zero order parame-

ter h¯qqi. In the high temperature quark-gluon plasma phase chiral symmetry is

restored, with the quarks unpaired. In the lower quark-gluon plasma phase to the

right, quarks are BCS paired with an order parameter hqqi, and chiral symmetry

weakly broken. In the region below EDA quarks remain paired, likely as diquarks,

and chiral symmetry is broken.

the familiar strongly interacting neutrons, protons, pi mesons, and other

hadrons. This phase contains a non-zero chiral condensate. As the tem-

perature or baryon density increases, matter enters the quark-gluon plasma

(QGP) phase. Along the line CD the transition is likely ﬁrst order, and at

densities below that at C, the transition is second order for massless quarks.

In the QGP, chiral symmetry is restored, h¯qqi = 0. Far to the right, at low

temperatures, the system is color-paired, as described above.

Not all the symmetries of the unrenormalized QCD Lagrangian are real-

ized in nature. In particular, owing to the axial anomaly, renormalization

breaks the axial U(1) symmetry producing an eﬀective attractive interac-

tion between six quarks.

This coupling leads to an attractive third order

coupling of the chiral condensate h¯qqi ≡ σ to itself,

as well an eﬀective

attractive interaction between the chiral condensate and the quark pairing

ﬁeld

hqqi ≡ d, schematically of the form −

cσ

− γd

σ, where c and d

are positive constants. With this axial anomaly term, the Ginzburg–Landau

interaction describing the coupled eﬀective σ and d ﬁelds is schematically

int

−

− γd

σ + λd

. (2)

October 4, 2010 10:17 World Scientiﬁc Review Volume - 9.75in x 6.5in ch20

518 G. Baym

The ﬁrst four terms describe the chiral ﬁeld self-interaction and the usual

Ginzburg–Landau terms for BCS pairing of quarks, while the ﬁnal two terms

describe the coupling of the chiral and pairing ﬁelds. Owing to this latter

coupling, the intermediate region around point A can develop a new critical

point at ﬁnite baryon density and low temperature (always below the onset of

pairing).

The symmetry group of color-ﬂavor locked paired quark matter

is in fact the same as that of chiral-symmetry-broken hadronic matter with

equal mass u, d and s quarks,

SU(3) × Z

, suggesting the possibility of

a continuous transition below the critical point from the paired quark state

to the hadronic phase. The solid line DE represents the transition from

quark pairing to hadrons. As we discuss in a moment, the region below the

critical point likely exhibits a BEC-BCS crossover, in which as the density

is decreased large BCS pairs become small diquarks.

6. BEC-BCS Crossover and the Deconﬁnement Transition

Historically, the ﬁelds of superconductivity and Bose–Einstein condensation,

which focused primarily on superﬂuid

He, developed along rather indepen-

dent paths. Thus, it was not surprising that the connection between the two

phenomena was not on the front burner. Indeed, the original BCS paper

comments on the newly proposed Schafroth, Butler and Blatt “quasichem-

ical approach” to superconductivity in which small electron molecules are

formed and Bose condense,

in the following footnote, “Our picture diﬀers

from that of Schafroth, Butler and Blatt, who suggest that pseudomolecules

of pairs of electrons of opposite spin are formed. They show if the size of the

pseudomolecules is less than the average distance between them, and if other

conditions are fulﬁlled, the system has properties similar to that of a charged

Bose–Einstein gas, including a Meissner eﬀect and a critical temperature of

condensation. Our pairs are not localized in this sense, and our transition

is not analogous to ‘a Bose–Einstein condensation.’ ” Shortly after the BCS

paper was written, Bardeen sent a letter to Dyson, who was a ﬁrm believer

in the equivalence of the two theories, emphasizing the diﬀerence of the two

theories: “We believe that there is no relation between actual superconduc-

tors and the superconducting properties of a perfect Bose–Einstein gas. The

key point in our theory is that the virtual pairs all have the same net mo-

mentum. The reason is not Bose–Einstein statistics, but comes from the

exclusion principle . . .”

We now understand more fully the connection of

the two approaches thanks to the work of Eagles,

Leggett,

and Nozi`eres

and Schmitt-Rink,

who showed how BCS pairs continuously transform

October 4, 2010 10:17 World Scientiﬁc Review Volume - 9.75in x 6.5in ch20

BCS from Nuclei and Neutron Stars to Quark Matter and Cold Atoms 519

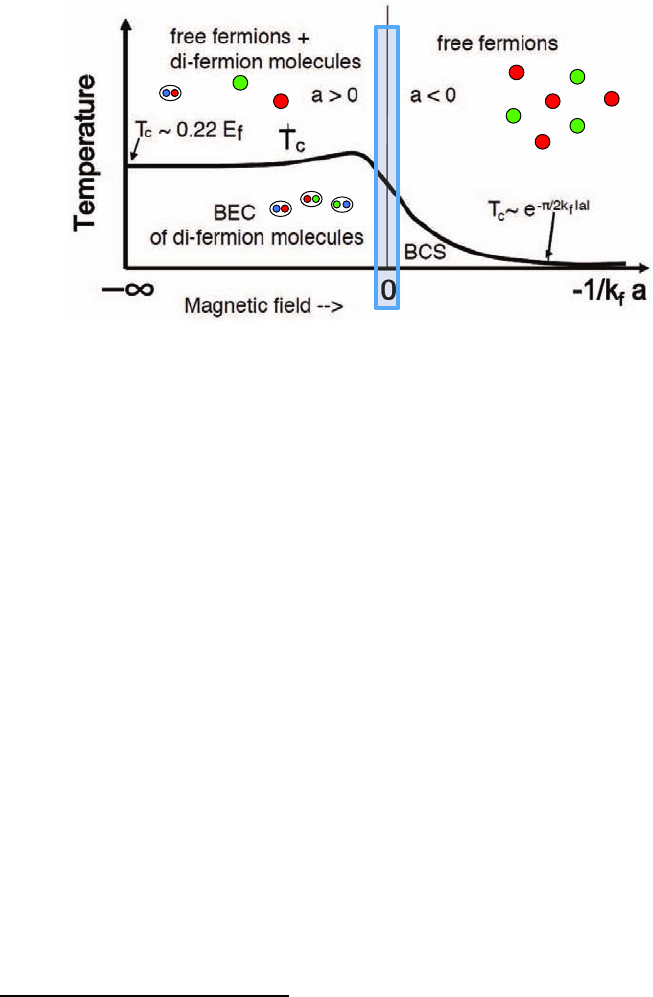
Fig. 5. Phase diagram of a gas of two equally populated hyperﬁne states of ultra-

cold atomic fermions as a function of the negative of the inverse scattering length a,

in units of the Fermi momentum. The continuous curve is the transition tempera-

ture for condensation, approaching the weakly interacting Bose–Einstein transition

temperature to the left and the BCS transition temperature to the right; E

is the

free particle Fermi energy. The transition between the BEC and BCS regions is a

smooth crossover.

into molecules with increasing interaction strength between the paired

fermions.

Figure 5 shows the ﬁnite temperature phase diagram of a gas of two

equally populated hyperﬁne states of ultracold fermionic atoms. The hor-

izontal axis is −1/k

a, where a is the s-wave scattering length, and k

the Fermi momentum of the gas. At small positive a, to the left of the

phase diagram, the system has strong bound states — di-fermion molecules

— which as the temperature is lowered undergo Bose condensation, while

at small negative a, to the right, the fermions become BCS paired at low

temperatures. Remarkably, in the region between these two extremes the

system undergoes a gradual crossover from a BEC superﬂuid of molecules

to a BCS paired superﬂuid.

41,42

Nothing dramatic happens as one goes

through “unitarity” (|a| → ∞); rather the molecules continuously expand

in size from tightly bound in the BEC regime to widely spaced pairs in the

Leon Cooper believes that Bardeen did, in fact, understand the connection, but

felt it wisest to focus on how the two pictures diﬀered. (Private communication to

G. Baym, March 2009). Leon’s own view on the BEC-BCS crossover is discussed

brieﬂy in his chapter in this volume.

October 4, 2010 10:17 World Scientiﬁc Review Volume - 9.75in x 6.5in ch20

520 G. Baym

BCS regime. The system remains superﬂuid, as veriﬁed in a rotating system

by the presence of quantized vortices from the BEC to BCS regimes.

The transition temperature rises slightly with increasing a > 0 from

the ideal Bose limit on the left, initially linear in a. Determining the ef-

fect of a repulsive interaction on the transition temperature of the ideal

Bose gas was controversial for over four decades,

and was only resolved a

decade ago.

The precise coeﬃcient of the linear rise can only be calculated

numerically.

The correspondences of the phase diagram of ultracold atomic fermions

with the phase diagram of dense QCD matter, Fig. 4, are apparent. At

very large baryon chemical potential, µ, and low temperature the matter

is BCS paired, as are the atomic systems at large −1/k

a and low tem-

perature. As the temperature increases the atomic system becomes a ﬂuid

of normal unpaired fermions, while the QCD system becomes an unpaired

plasma. Furthermore, with decreasing −1/k

a, the atomic system contin-

uously transforms into a Bose–Einstein condensate of di-fermion molecules;

similarly QCD matter at low temperature goes from the color-paired states

at large µ smoothly under the critical point, to the coexistence state in which

both hqqi and h¯qqi are non-zero.

Were the color symmetry group only SU(2), the analogy between the

atomic and quark case would be strong — the baryons would be diquark

pairs, bosons, which would go over into BCS pairs at higher densities, just as

the atomic molecules slowly expand into BCS pairs with increasing magnetic

ﬁeld through a Feshbach resonance. However in the real world of SU(3)-

color the baryons are three quark objects; understanding how the system

crosses over from strong three-quark correlations at low densities to two-

quark correlations at high densities remains an open issue. Since at lower

densities two-ﬂavor 2SC color pairing is favored, the atomic systems raise

the possibility that at low temperatures three-quark correlations could enter

through (2SC) BCS pairs shrinking into diquarks as the system enters the

coexistence region, turning continuously into a strongly interacting diquark

BEC. Then at line DE in Fig. 4, the diquarks would bind to the unpaired

quarks to form baryons at lower density.

A simple simulation of this transition with ultracold atoms, via binding of bosonic

atoms (analogs of diquarks) with fermionic atoms (analogs of the unpaired quarks)

into molecules, the analog of the nucleon, is suggested in Ref. 47. More generally,

atomic fermionic systems with three internal states, e.g. the three lowest hyper-

ﬁne levels of

Li, oﬀer the possibility of studying laboratory analogs of the QCD

hadronization-deconﬁnement transition with pairing correlations.

–