Cooper L.N., Feldman D. (Eds.) BCS: 50 Years

Подождите немного. Документ загружается.

September 14, 2010 15:18 World Scientiﬁc Review Volume - 9.75in x 6.5in ch14

Breaking Translational Invariance by Population Imbalance 341

yields a pairing amplitude Ψ

σσ

) which depends upon the direction k

on the Fermi surface.

The fundamental property of Ψ

σσ

is its behavior as a two-fermion wave

function in many respects. This expresses the fact that a superconducting or-

der parameter is not the thermal expectation value of a physical observable,

but rather a complex (pseudo) wave function describing quantum phase cor-

relations on the macroscopic scale of the superconducting coherence length.

Its phase is a direct signature of the broken gauge invariance in the super-

conducting condensate.

The Pauli principle requires Ψ

σσ

to be antisymmetric under the inter-

change of particles Ψ

σσ

) = −Ψ

(−k

). In addition, it transforms like

a two-fermion wave function under rotations in position and spin space and

under gauge transformations. The transformation properties yield a general

classiﬁcation scheme for the superconducting order parameter which is rep-

resented by a 2 × 2 matrix in (pseudo) spin space. It can be decomposed

into an antisymmetric “singlet” (s) and a symmetric “triplet” (t) contribu-

tion according to Ψ(k

) = Ψ

) + Ψ

) with Ψ

) = φ(k

)iσ

and Ψ

) =

µ=1

)σ

iσ

, where σ

with µ = 1, 2, 3 denote

the Pauli matrices. Antisymmetry, Ψ(k

) = −Ψ

(−k

), requires φ(k

) =

φ(−k

) and d

) = −d

(−k

) for the complex orbital functions φ(k

)

and d

The general classiﬁcation scheme for superconducting order parameters

proceeds from the behavior under the transformations of the symmetry group

G of the Hamiltonian. It consists of the crystal point group G or the SO(3)

in the case of an isotropic liquid, the spin-rotation group SU(2), the time-

reversal symmetry group K, and the gauge group U(1). A comprehensive

description is given e.g. in Ref. 15 and references therein.

Population imbalance aﬀects only opposite “spin” pairs, i.e. pairs formed

by diﬀerent species which occur in the even-parity (spin-singlet) supercon-

ductors as well as the d

-component of a triplet state. In the following discus-

sion, we shall focus on even-parity (spin-singlet) superconductors belonging

to a one-dimensional representation Γ of the symmetry group. These states

are characterized by a complex scalar function, g (k

), which can have zeros,

symmetry-imposed or accidental, on the Fermi surface. If Γ is the unity rep-

resentation, the superconductor is called “conventional”, otherwise we call

it “unconventional”.

The classiﬁcation scheme described above refers to the symmetry prop-

erties of the pair amplitudes with respect to the relative variable which re-

ﬂects the short-ranged quasiparticle interaction varying on the atomic scale.

September 14, 2010 15:18 World Scientiﬁc Review Volume - 9.75in x 6.5in ch14

342 G. Zwicknagl and J. Wosnitza

Considering the separation of length scales, we adopt the same scheme to

classify the variation with the relative variable of inhomogeneous order pa-

rameters speaking of s- and d-wave, conventional and unconventional FFLO

states. A textured order parameter which varies periodically with the center-

of-mass variable R on the scale of the coherence length may break both

translational and rotational symmetry. The general classiﬁcation scheme for

a periodic order parameter has not yet been worked out. An interesting

phenomenon is the potential spontaneous breaking of relative symmetries in

FFLO states. The orientation of the “crystalline” order parameter is deter-

mined by anisotropies of the normal-state properties but also by anisotropies

in the order parameter of the homogeneous reference system.

2.2. Population imbalance and breaking of translational

symmetry

To start with, we consider a two-component Fermi liquid at T = 0 where the

two species are denoted by ↑ and ↓, respectively. The elementary excitations

in the normal state are weakly interacting quasiparticles with dispersion (k)

where the energies are conveniently measured relative to the average chem-

ical potential µ. The quasiparticles feel a short-ranged attraction V which

causes the instability of the normal state. Adopting mean-ﬁeld approxima-

tion and introducing the abbreviation

∆ (k; q) =

V (k, −k; k

, −k

)

−k

↓

↑

(3)

for the eﬀective pair ﬁeld leads to the separable model Hamiltonian

H =

H(k) + const, (4)

where

H(k) =







k +



− δµ



†

↑







−k +



+ δµ



†

−k+

↓

−k+

↓

+ ∆

∗

(k; q) c

−k+

↓

↑

+ ∆ (k; q) c

†

↑

†

−k+

↓

. (5)

The operators c

†

kσ

) create (annihilate) a quasiparticle in state kσ, δµ

denotes the chemical-potential mismatch. In Eq. (4), the constant corrects

for double counting of interactions. An ultraviolet cut-oﬀ is introduced as

indicated by the prime in the sum in Eq. (3). As written, Eq. (5) is the usual

Bardeen-Cooper-Schrieﬀer (BCS) Hamiltonian for an order parameter with

ﬁnite center-of-mass momentum q varying in real space ∼ e

iq·R

17,18

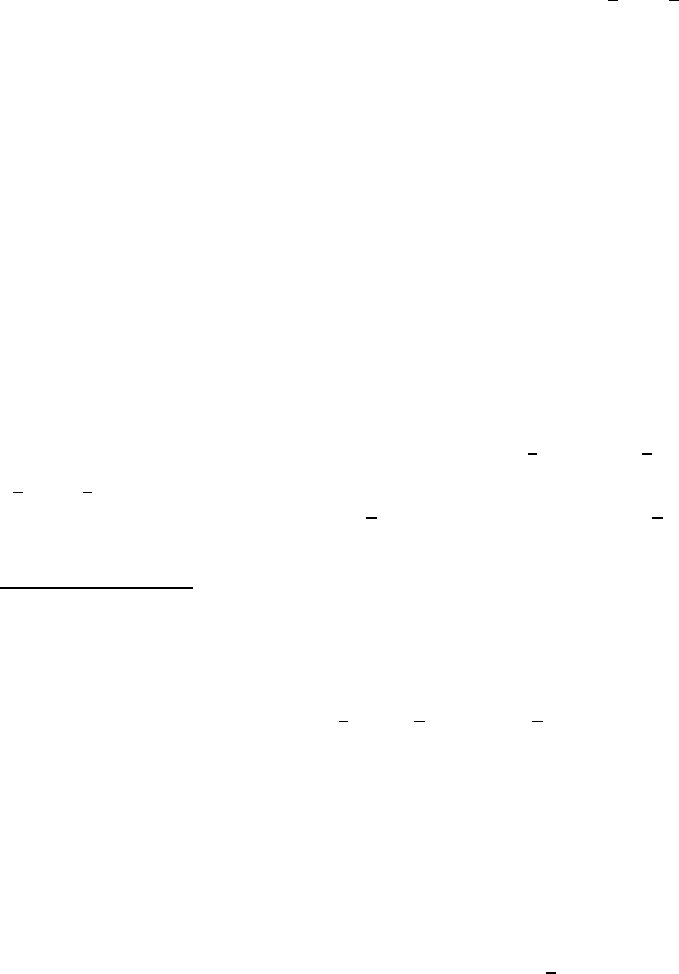
September 14, 2010 15:18 World Scientiﬁc Review Volume - 9.75in x 6.5in ch14

Breaking Translational Invariance by Population Imbalance 343

assume that the corresponding length scale is set by the coherence length

which implies q ∼ 1/ξ

 k

. In that respect, the modulated order

parameters considered here diﬀer from those of antiferromagnetic supercon-

ductors

19,20

where the staggered ﬁeld induces contributions hc

−k

↓

↑

with q ∼ k

The thermodynamic properties of the model Eq. (4) can be deduced from

the free energy. For a given chemical-potential mismatch the latter is cal-

culated by treating the center-of-mass momentum q and the pair potential

∆ (k; q) as variational parameters. The values of the latter are subsequently

determined so as to minimize the free energy. Proceeding along these lines

yields directly the (meta-) stable states. The traditional approach based

on solving the self-consistency equation for the order parameter yields the

stationary points of the free energy which include (meta-) stable as well as

unstable phases.

Following this line of thought we begin by calculating the eigenvalues

and eigenstates of the model Hamiltonian for a given chemical-potential

mismatch δµ, center-of-mass momentum q, and pair potential ∆ (k; q).

Since all pair Hamiltonians H(k) commute the eigenfunctions of the

BCS Hamiltonian Eq. (4) will be products of the eigenstates of H(k). The

operators H(k) are easily diagonalized in the basis c

†

↑

|0i, c

†

−k+

↓

|0i,

†

↑

†

−k+

↓

|0i, and |0i where the single-particle states |k; ↑i and |k; ↓i are

eigenstates with energies E

k↑

= 



k +



− δµ and E

k↓

= 



−k +



δµ, respectively. The characteristic feature of the superconducting state

are the pair states |k; −i and |k; +i with energies E

∓

(k) =  (k) ∓

( (k))

+ |∆ (q; k)|

, which are obtained as coherent superpositions of the

two-particle states and the empty state in close analogy to bonding and

anti-bonding states in molecular physics. We explicitly used the fact that

the anticipated center of mass momentum of the Cooper pairs is small on the

scale of the Fermi momentum setting

((k +

) + (−k +

)) ' (k). Tran-

sitions between the diﬀerent branches labeled by ν = ±, ↑, ↓ are described

in terms of ladder operators, the Bogoliubov operators.

Figure 1 displays the eigenvalues for the unperturbed balanced supercon-

ductor (a) and one with imbalance and ﬁnite center of mass momentum (b)

and (c). In the unperturbed superconductor, the bound pair states |k; −i

are energetically more favorable than the single-particle states. Both the

chemical-potential mismatch δµ and ﬁnite center-of-mass momentum q, shift

the single-particle state relative to the bound pair states which remain un-

aﬀected. For a ﬁxed direction on the Fermi surface, δµ and

) ·q can

September 14, 2010 15:18 World Scientiﬁc Review Volume - 9.75in x 6.5in ch14

344 G. Zwicknagl and J. Wosnitza

Fig. 1. Eigenvalues E

with ν = −, ↑, ↓, + of the pair Hamiltonian Eq. (5) for

∆ > 0 versus kinetic energy (k) of the normal-state quasiparticles with Q as deﬁned

in the text. In a homogeneous superconductor without imbalance (δµ = 0, q = 0,

i.e. Q = 0) (left panel) the ground state is formed as a product of bound-pair states,

i.e. ν (k) = − or all momenta k. Population imbalance δµ > 0 in a homogeneous

superconductor as well as ﬁnite center-of-mass momenta q 6= 0, i.e. Q 6= 0 (middle

and right panel) may reduce the energies of the single particle states E

↑(↓)

below

those of the bound-pair states. The Zeeman splitting may be partially compensated

by ﬁnite center-of-mass momentum. Forming a many-particle state with single-

particle states in the vicinity of the Fermi energy ξ = 0 reduces the phase space for

pairing. At the intersection of the branches, the character of the compromise state

changes abruptly. This leads to singularities in the ground-state energy as function

of ∆, δµ, and q.

be combined to mutually compensate the shifts. The appropriate q-vector

depends, of course, on the Fermi velocity v

) which varies on the Fermi

surface. As a consequence, it is impossible to fully compensate a mismatch

δµ for all fermions at the Fermi surface in two (2D) and three-dimensional

(3D) superconductors by choosing a single wave vector q. Depending on

the relative size of



δµ −

) · q



and ∆ (k; q) we may have partial

compensation (see Fig. 1(b) and Fig. 1(c)). In a one-dimensional (1D) su-

perconductor, on the other hand, the mismatch δµ can be fully compensated

resulting in the absence of a limiting δµ value.

Having diagonalized the mean-ﬁeld Hamiltonian for arbitrary ∆(k; q),

δµ and q we now turn to a discussion of the ground state of the system

which — like any eigenstate of the model Hamiltonian Eq. (4) — is given

as a product |Ψ {ν (k)}i =

|k; ν(k)i. The index function ν (k) = ∓, ↑, ↓

speciﬁes the state to be selected for a given k-vector. At this point, we

would like to emphasize that the product must run over all k states in order

to obtain an eigenfunction of the model Hamiltonian. This feature reﬂects

the highly correlated nature of the states. Any eigenstate is characterized

September 14, 2010 15:18 World Scientiﬁc Review Volume - 9.75in x 6.5in ch14

Breaking Translational Invariance by Population Imbalance 345

by the momentum-space function ν (k) which can be viewed as an analogue

of the momentum-distribution function. The corresponding energy, given by

E ({ν (k)}) =

ν(k)

(k), (6)

is minimal when the state ν

(k) with the lowest value for every k is se-

lected. Comparing the energies of the bound pair states E

−

(k) to those of

the single-particle states E

↑

(k) and E

↑

(k) in Fig. 1 shows that the BCS

wave function built as a product of bound pair states |Ψ

0BCS

i =

|k; −i

gives the lowest energy for weak imbalance (δµ < ∆) and long-wavelength

modulation (

q < ∆).

The central focus of the present article are compromise states built from

a combination of bound pair states and single-particle states. These states

include the gapless homogeneous BP phase where the normal majority com-

ponent is found in the immediate vicinity of the Fermi surface. Allowing

for ﬁnite center-of-mass momentum q, we arrive at partially gapped states

where quasiparticle excitations of both the majority and the minority com-

ponents may be present at k

. The gapless regions do not contribute to

pairing, they are “blocked”. In general, blocking reduces the energy gain

due to pair formation and, consequently, destabilizes the superﬂuid state.

Treating ∆ and q as independent variables, the energy gain due to pair

formation for given δµ is easily evaluated from

∆E

(∆, δµ, q)

min

(k) −

k,σ

( (k) + σδµ) Θ (−( (k) + σδµ)) + const, (7)

with the Heaviside function Θ(x) = 0 for x < 0 and Θ(x) = 1 otherwise. The

ﬁrst two terms are the quasiparticle contribution while the constant corrects

for double counting of interaction energies in the quasiparticle contribution.

Before we turn to the solution we simplify the notation and introduce

dimensionless variables. We explicitly account for the fact that the relevant

degrees of freedom are restricted to the immediate vicinity of the Fermi

surface. As a result, the summation over the quasiparticle states separate

into products of integrals over the Fermi surface parameterized by k

and

energy integrations over ξ

··· = N(0)

w (k

) dk

dξ ··· = N (0)



dξ ···



F S

. (8)

September 14, 2010 15:18 World Scientiﬁc Review Volume - 9.75in x 6.5in ch14

346 G. Zwicknagl and J. Wosnitza

We introduced the density of states at the Fermi energy, N(0), and h···i

F S

as a short-hand notation for the Fermi-surface integral

w (k

) dk

··· with

the normalized weight function hw (k

F S

= 1 given by the Fermi velocity

w (k

) ∝

. This allows us to fully account for anisotropies in the

Fermi wave vector and in the eﬀective mass. The anisotropic gap function

is given by ∆

g (k

) with the normalized function

|g (k

= 1. All

energies are measured in units of the order-parameter amplitude ∆

which

minimizes the energy diﬀerence Eq. (7) of the homogeneous reference system

q = 0 without imbalance δµ = 0. We deﬁne Q (k

) =

)·q

and mea-

sure the center-of-mass momentum in units of the inverse coherence length.

Finally, the coupling constant and the ultra-violet cut-oﬀ are eliminated in

favor of the energy gap ∆

of the balanced reference system and we arrive

∆E

(∆

, δµ, q) /N (0)

= −

|∆



(δµ + Q (k

))



F S

−



(δµ + Q (k

))



(δµ + Q (k

))

− |∆

|g (k





F S

+ |∆

|g (k

Re log

(δµ + Q (k

))

(δµ + Q (k

))

− |∆

|g (k

∆

|g (k

F S

(9)

The expression has singularities which correspond to the bounds of the

broken-pair regions. This fact already indicates that an expansion of the

ground-state energy in terms of the order-parameter amplitude ∆ is likely

to fail. The radius of convergence of such an expansion will depend upon the

dimensionality of the system under consideration. The consequences were

discussed in detail by Combescot and Mora.

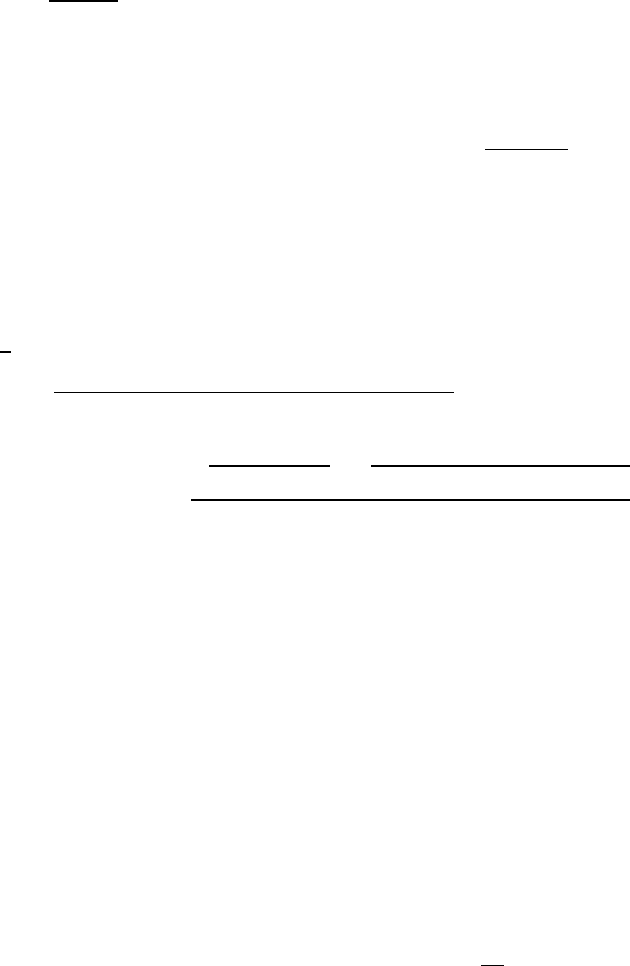
The evolution of the ground-state energy of a homogeneous supercon-

ductor with imbalance is displayed in Fig. 2 for a homogeneous isotropic

s-wave superconductor and its d

−y

-wave-counterpart. The characteris-

tic features for the isotropic s-wave superconductor can be summarized as

follows: for large values of the chemical-potential mismatch δµ > ∆

, the

energy increases monotonically with ∆ and the normal state ∆ = 0 is the

only stable phase. As δµ is lowered below δµ = ∆

, the BCS ground state

∆ = ∆

appears as a metastable state and we enter the two-phase regime.

The latter extends down to the supercooling ﬁeld δµ =

∆

below which the

system must be superconducting. In the two-phase regime, the local minima,

September 14, 2010 15:18 World Scientiﬁc Review Volume - 9.75in x 6.5in ch14

Breaking Translational Invariance by Population Imbalance 347

Fig. 2. Contour plot of variation with δµ and ∆ of the energy gain

∆E

(∆

q=0

, δµ, q = 0)/(N(0)∆

) (see Eq. (7)) for the homogeneous s-wave (left

panel) and d

−y

-wave (right panel) superconductor. Solutions of the selfconsis-

tency equation correspond to stationary points of ∆E

with respect to variations of

∆

q=0

. The order-parameter amplitude ∆

q=0

and the chemical-potential mismatch

δµ are measured in units of the order-parameter amplitude ∆

in the BCS ground

state of the corresponding balanced reference system. The latter corresponds to

the minimum of ∆E

along the δµ = 0-line. For the homogeneous s-wave state,

∆E

has a (local) minimum at ∆/∆

= 1 as long as δµ/∆

< 1. The BCS

state (solid line) therefore persists as a (meta-) stable state up to the superheat-

ing “ﬁeld” δµ/∆

= 1. For small values of the mismatch δµ/∆

< 0.5, the BCS

state is the only minimum of ∆E

. At the supercooling “ﬁeld” δµ/∆

= 0.5, the

normal state ∆/∆

= 0 becomes a (local) minimum. The homogeneous systems

exhibit a rather broad two-phase regime for 0.5 ≤ δµ/∆

≤ 1. In this δµ-range,

∆E

has a local maximum which corresponds to Sarma’s unstable solution of the

selfconsistency equation (dashed line). The qualitative behavior of ∆E

for a ho-

mogeneous d

−y

-wave order parameter closely parallels that of the homogeneous

isotropic s-wave superconductor. The quantitative diﬀerences, however, are due to

the presence of low-energy quasiparticle excitations.

i.e. the normal state ∆ = 0 and the usual BCS state ∆ = ∆

, are separated

by a well which is centered at the line ∆ = ∆

δµ

∆

− 1 which was found by

Sarma.

At the Chandrasekhar–Clogston limit, δµ =

∆

√

, the normal phase

and the BCS state become degenerate and a ﬁrst-order transition between

the normal and the superconducting state occurs. It is important to note

that there is no stable BP state, superconducting (meta-) stable states oc-

cur only for ∆ = ∆

≥ δµ. The main features are also present in the case

of a d

−y

-wave order parameter which is likely to occur in many super-

conductors with strongly correlated electrons. The presence of low-energy

September 14, 2010 15:18 World Scientiﬁc Review Volume - 9.75in x 6.5in ch14

348 G. Zwicknagl and J. Wosnitza

Fig. 3. Variation with chemical-potential mismatch δµ/∆

, order-parameter am-

plitude ∆

/∆

, and length of modulation vector Q =

∆

of the energy diﬀerence

∆E

from Eq. (9) for (a) an isotropic three-dimensional (3D), (b) an isotropic two-

dimensional (2D), and (c) one-dimensional (1D) Fermi surface. All energies are

measured in units of the order-parameter amplitude ∆

characterizing the BCS

ground state of the homogeneous (q = 0) balanced (δµ = 0) reference system. In

the ﬁlled regions, the superconducting solution is energetically more favorable than

the normal state (∆E

< 0). The boundary surface corresponds to combinations

of δµ/∆

, ∆

/∆

, and Q =

∆

for which the energy of the superconducting

solution equals that of the normal state, i.e. ∆E

= 0. The plane δµ/∆

= 1/

√

corresponds to the Chandrasekhar–Clogston limit for the ﬁrst-order transition be-

tween the homogeneous superconducting and normal states. For modulated states

Q 6= 0, pair formation can lead to energy gain for chemical-potential mismatch

δµ/∆

exceeding the Chandrasekhar–Clogston limit.

excitations, however, reduces the energy-gap opening at the superheating

ﬁeld.

We next turn to the case of ﬁnite-q pairing. As pointed out before, the

possible compensation of the chemical-potential mismatch depends on the

dimensionality of the system. This is clearly evident from Fig. 3 which shows

the regions in δµ-q-∆ space where the energy of the superconducting state

is lower than that of the normal phase, ∆E

(∆

, δµ, q) ≤ 0, for isotropic

3D and 2D as well as for 1D superconductors with s-wave order parameter.

The limiting value of the chemical-potential mismatch δµ/∆

is given by the

maximum which only slightly exceeds the Chandrasekhar–Clogston limit in

3D. In 2D, the limiting value is enhanced and coincides with the beginning of

the two-phase regime. The singularities for small ∆q/∆

give rise to highly

anomalous properties to be discussed in the subsequent section. The absence

of a limiting mismatch in 1D is obvious.

September 14, 2010 15:18 World Scientiﬁc Review Volume - 9.75in x 6.5in ch14

Breaking Translational Invariance by Population Imbalance 349

At ﬁnite temperatures T > 0, the free-energy gain due to pairing is given

∆F (∆

, δµ, q; T ) = −N (0)



−



(δµ − Q (k

))



F S

+ |∆

+ 2πk

∞

`=0



2Re



(ω

+ i (δµ − Q (k

)))

+ |∆

)



F S

− 2ω

−

|∆



(10)

where ω

= πk

T (2` + 1) are the fermionic Matsubara frequencies and T

denotes the superconducting transition temperature of the balanced refer-

ence system. Of particular interest is the second-order transition from the

normal phase to a superconducting state ∆

iq·r

which occurs at a critical

mismatch δµ(T ) given by the linearized selfconsistency equation (linearized

stationarity condition) for ∆F (∆

, δµ, q; T ). The latter is given by the im-

plicit equation

=ψ





−min



) Re ψ



2πk

(δµ (T )+Q (k

))



F S

(11)

where ψ (z) is Euler’s digamma function. The optimal modulation vector de-

pends on the anisotropies of the normal-state quasiparticle dispersion and the

superconducting order parameter as given by v

) and g (k

). The vari-

ation with T has been analyzed in great detail by Saint-James and Sarma

for the s-wave case. The formal key to the phase diagram is the variation

with x of the curvature −Re ψ



+ ix



which is negative for small values of

the argument and changes sign at x = 0.304. This implies that close to the

transition temperature T

, i.e. for small values of δµ the homogeneous state

q = 0 is formed. In this temperature range, the critical mismatch follows a

universal curve independent of the details of the system under consideration.

With decreasing temperature a tricritical point appears at T = 0.55T

, be-

low which the transition from the normal state into a modulated state with

q 6= 0 occurs. The critical value for the mismatch, assuming q = 0, becomes

the supercooling ﬁeld below which the homogeneous superconductor is the

thermodynamically stable phase.

The inﬂuence of dimensionality on the δµ–T phase diagram is clearly

evident from Fig. 4 (left panel) which displays the variation with tempera-

September 14, 2010 15:18 World Scientiﬁc Review Volume - 9.75in x 6.5in ch14

350 G. Zwicknagl and J. Wosnitza

0.0 0.5 1.0

0.0

0.5

1.0

T/T

δµ/∆

homogeneous

superconductor

normal state

2−phase

0.0 0.5 1.0

0.0

0.4

0.8

1.2

T/T

δµ/∆

homogeneous

superconductor

normal state

Fig. 4. Comparison of δµ-T phase diagrams. Left panel: s-wave superconductor.

For temperatures above the tricritical point (black dot) the normal state becomes

unstable relative to a homogeneous superconducting state (for suﬃciently low δµ).

Below the tricritical point, the homogeneous superconducting phase can coexist with

the normal state in a δµ regime bound by the supercooling ﬁeld (dotted line) and the

superheating ﬁeld (dash-dotted line). In a 3D system with spherical Fermi surface a

second-order transition from the normal state to an FFLO state (solid line) is found

for δµ slightly above the critical value for the ﬁrst-order transition between the

homogeneous phases (dashed line). For a 2D system with cylindrical Fermi surface

the second-order transition coincides with the superheating ﬁeld of the homogeneous

phases. Right panel: d-wave superconductor. Second-order transition from the

normal to the d

−y

-wave FFLO state in a 2D superconductor with cylindrical

Fermi surface for modulation vector parallel to the nodal direction (dashed line)

and anti-nodal direction (solid line). The supercooling ﬁeld (dotted line) is included

for comparison.

ture of the critical mismatch for s-wave superconductors with spherical and

cylindrical Fermi surfaces as well as the two-phase regime for homogeneous

superconductivity bounded by the superheating and the supercooling ﬁelds

as well as the corresponding line of ﬁrst-order transitions. In an anisotropic

superconductor the variation with angle of the gap function selects the opti-

mal orientation of the modulation vector q. The latter may change discon-

tinuously with temperature leading to kinks in the critical-mismatch curve.

This eﬀect was predicted for superconductors with a d

−y

-wave order pa-

rameter and a cylindrical Fermi surface by Maki and Won

as shown in

Fig. 4 (right panel).

The second-order transition lines give good qualitative insight into the

overall behavior of superconductors with population imbalance. The explicit

evaluation of the full phase diagram including potential ﬁrst-order transitions