Coburn J.W. Algebra and Trigonometry
Подождите немного. Документ загружается.


60 CHAPTER R A Review of Basic Concepts and Skills R-60
Quotient Property of Radicals
If and represent real-valued expressions with then
and .
Many times the product and quotient properties must work together to simplify a
radical expression, as shown in Example 10.
EXAMPLE 10
Simplifying Radical Expressions
Simplify each expression:
a. b.
Solution
a. b.
Now try Exercises 27 and 28
Radical expressions can also be simplified using rational exponents.
EXAMPLE 11
Using Rational Exponents to Simplify Radical Expressions
Simplify using rational exponents:
a. b. c. d.
Solution
a. b.
c. d.
or
Now try Exercises 29 and 30
D. Addition and Subtraction of Radical Expressions
Since 3x and 5x are like terms, we know If the sum becomes
illustrating how like radical expressions can be combined. Like
radicals are those that have the same index and radicand. In some cases, we can iden-
tify like radicals only after radical terms have been simplified.
31
3
7 51
3
7 81
3
7,
x 1
3
7,3x 5x 8x.
2
6
m
5
1
6
x x
1
6
m
5
6
x
1
2
#
1
3
m
1
3
1
2
1x
1
2
2
1
3
1
3
m1m m
1
3
m
1
2
2
3
1x 2
3
x
1
2
v
2
1
3
v 6p
2
q
2
1q
v
6
3
v
1
3
6p
2
q
2
q
1
2
v
7
3
6p
2
q
1
4
2
1
2
2
v
3
3
#
v
4
3
36
1
2
p
4
2
q
5
2
v2
3
v
4
v
1
#
v
4
3
236p
4
q
5
136p
4
q
5
2
1
2
1
3
m1m2
3
1xv2
3
v
4
236p
4
q
5
31
3
3
5x
1
3
27
#
3
5x
29a
4
A
3
81
125x
3
1
3
81
2
3
125x
3
218a
5
22a
B
18a
5
2a
A
3
81
125x
3
218a
5
22a
1
n
A
1
n
B
A
n
A
BA
n
A
B
1
n
A
1
n
B
B 0,1
n
B 1
n
A
3a
2
C. You’ve just reviewed
how to use properties of
radicals to simplify radical
expressions
College Algebra—
cob19413_chR_001-072.qxd 14/10/2008 12:08 PM Page 60 EPG 204:MHDQ069:mhcob%0:cob2chR:
R-61 Section R.6 Radicals and Rational Exponents 61
EXAMPLE 12
Adding and Subtracting Radical Expressions
Simplify and combine (if possible).
a. b.
Solution
a. simplify radicals:
like radicals
result
b.
simplify radicals
result
Now try Exercises 31 through 34
E. Multiplication and Division of Radical Expressions;
Radical Expressions in Simplest Form
Multiplying radical expressions is simply an extension of our earlier work. The mul-
tiplication can take various forms, from the distributive property to any of the special
products reviewed in Section R.3. For instance, even if
A or B is a radical term.
EXAMPLE 13
Multiplying Radical Expressions
Compute each product and simplify.
a. b.
c. d.
Solution
a. distribute;
simplify:
result
b. F-O-I-L
result
c.
result
d.
simplify each term
result
Now try Exercises 35 through 38
One application of products and powers of radical expressions is to evaluate
certain quadratic expressions, as illustrated in Example 14.
EXAMPLE 14
Evaluating a Quadratic Expression
Show that when is evaluated at the result is zero.
Solution
original expression
substitute for x
multiply
commutative and associative properties
Now try Exercises 39 through 42
0 ✓
14 3 8 12 1413
4132
4 413
3 8 413 1
2 23 12 132
2
412 132 1
x
2
4x 1
x 2 13
,x
2
4x 1
11 612
9 612 2
13 12
2
2
132
2
21321122 1122
2
x
2
7
1A B21A B2 A
2
B
2
1x 1721x 172 x
2
1172
2
3015 20130
1215 20130 1815
1212 613213110 1152 6120 2130 18130 6145
1512 60
218 322 513212 1202132
1232
2
3 5 13116 4132 5118 201132
2
13 222
2
1x 2721x 272
1222
623213210 2152523126 4232
1A B2
2
A
2
2AB B
2
,
x2
3
2x
2
2x2
3
2x
2
3x2
3
2x
2
2
3
16x
5
x2
3
54x
2
2
3
8
#
2
#
x
3
#
x
2
x2
3
27
#
2
#
x
2
715
315 415
245 29
#
5; 220 24
#
5 145 2120 315 212152
2
3
16x
5
x2
3
54x
2
145 2120
D. You’ve just reviewed
how to add and subtract
radical expressions
LOOKING AHEAD
Notice that the answer for
Example 13(c) contains no
radical terms, since the outer
and inner products sum to
zero. This result will be used
to simplify certain radical
expressions in this section
and later in Chapter 1.
extract roots and
simplify
1A B2
2
A
2
2AB B
2
College Algebra—
cob19413_chR_001-072.qxd 14/10/2008 12:08 PM Page 61 EPG 204:MHDQ069:mhcob%0:cob2chR:

62 CHAPTER R A Review of Basic Concepts and Skills R-62
When we applied the quotient property in Example 10, we obtained a denomina-
tor free of radicals. Sometimes the denominator is not automatically free of radicals,
and the need to write radical expressions in simplest form comes into play. This process
is called rationalizing the denominator.
Radical Expressions in Simplest Form
A radical expression is in simplest form if:
1. The radicand has no perfect nth root factors.
2. The radicand contains no fractions.
3. No radicals occur in a denominator.
As with other types of simplification, the desired form can be achieved in various
ways. If the denominator is a single radical term, we multiply the numerator and
denominator by the factors required to eliminate the radical in the denominator [see
Examples 15(a) and 15(b)]. If the radicand is a rational expression, it is generally easier
to build an equivalent fraction within the radical having perfect nth root factors in the
denominator [see Example 15(c)].
EXAMPLE 15
Simplifying Radical Expressions
Simplify by rationalizing the denominator. Assume
a. b. c.
Solution
a. multiply numerator and denominator by
simplify—denominator is now rational
b. multiply using two additional factors of
product property
c.
the denominator is now a perfect cube—simplify
result
Now try Exercises 43 and 44
In some applications, the denominator may be a sum or difference containing a
radical term. In this case, the methods from Example 15 are ineffective, and instead
we multiply by a conjugate since If either A or B is a
square root, the result will be a denominator free of radicals.
1A B21A B2 A
2
B
2
.
2
3
6a
2
2a
2
B
3
6a
2
8a
6
A
3
3
4a
4
B
3
3
4a
4
#
2a
2
2a
2
2
3
x
3
x
72
3
x
2
x
72
3
x
2
2
3
x
3
1
3
x
7
1
3
x
711
3
x211
3
x2
1
3
x11
3
x211
3
x2
223
51232
2
223
15
23
2
523
2
523
#
23
23
A
3
3
4a
4
7
1
3
x
2
523
a, x 0.
is the smallest perfect cube with 4 as a factor;
is the smallest perfect cube with as a factora
4
a
4
#
a
2
a
6
4
#
2 8
College Algebra—
cob19413_chR_001-072.qxd 14/10/2008 12:08 PM Page 62 EPG 204:MHDQ069:mhcob%0:cob2chR:
R-63 Section R.6 Radicals and Rational Exponents 63
EXAMPLE 16
Simplifying Radical Expressions Using a Conjugate
Simplify the expression by rationalizing the denominator.
Write the answer in exact form and approximate form
rounded to three decimal places.
Solution
simplify
exact form
approximate form
Now try Exercises 45 through 48
F. Formulas and Radicals
A right triangle is one that has a angle. The longest side (opposite the right angle)
is called the hypotenuse, while the other two sides are simply called “legs.” The
Pythagorean theorem is a formula that says if you add the square of each leg, the result
will be equal to the square of the hypotenuse. Furthermore, we note the converse of this
theorem is also true.
Pythagorean Theorem
1. For any right triangle with legs a and b and hypotenuse c,
2. For any triangle with sides a, b,and c, if
then the triangle is a right triangle.
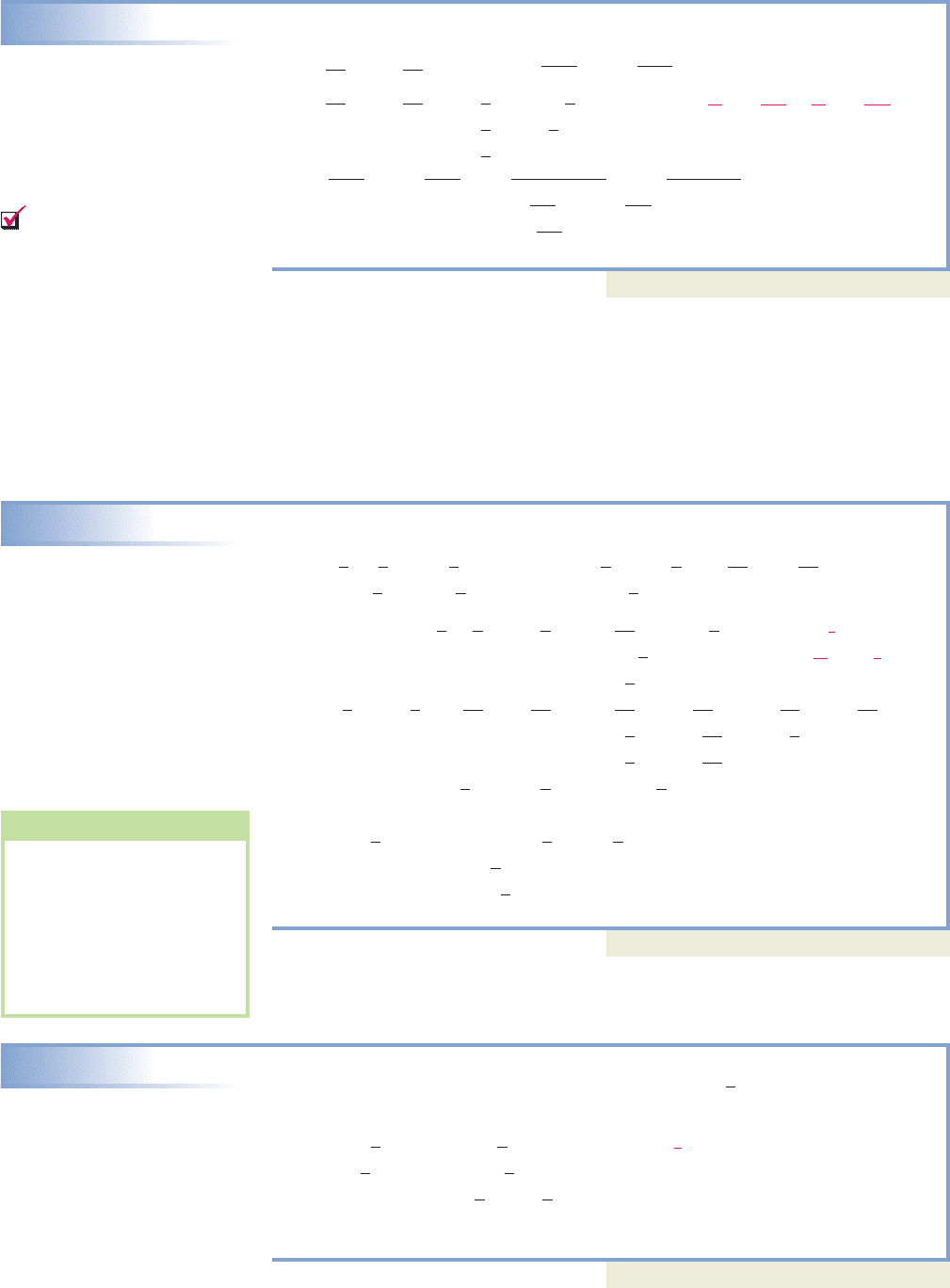
A geometric interpretation of the theorem is given in the figure, which shows
3
2
4
2
5
2
.
a
2
b
2
c
2
,
a
2
b
2
c
2
90°
3.605
326
522
4
326
222 322
6 2
226
222 218 26
1262
2
1222
2
2 23
26 22
2 23
26 22
#
26 22
26 22
2 23
26 22
E. You’ve just reviewed
how to multiply and divide
radical expressions and write
a radical expression in
simplest form
Hypotenuse
Leg
Le
g
90
5
4
3
Area
16 in
2
Area
9 in
2
Area
25 in
2
13
5
12
5
2
12
2
13
2
25 144 169
13
5
12
5
2
12
2
13
2
25 144 169
7
2
24
2
25
2
49 576 625
7
25
24
a
2
b
2
c
2
general case
c
a
b
EXAMPLE 17
Applying the Pythagorean Theorem
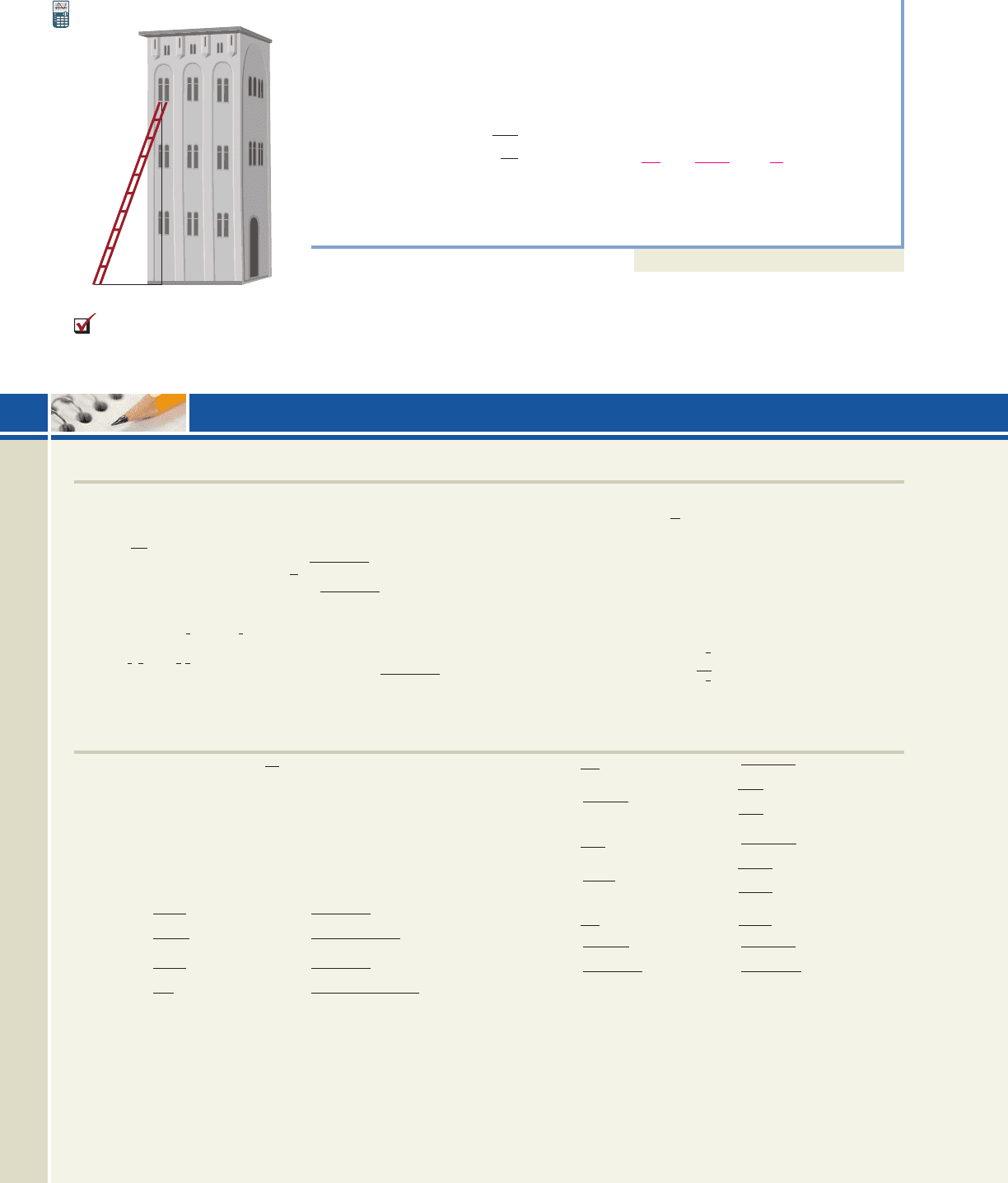
An extension ladder is placed 9 ft from the base of a building in an effort to reach a
third-story window that is 27 ft high. What is the minimum length of the ladder
required? Answer in exact form using radicals, and approximate form by rounding
to one decimal place.
multiply by the conjugate
of the denominator
FOIL
difference of squares
College Algebra—
cob19413_chR_001-072.qxd 14/10/2008 12:08 PM Page 63 EPG 204:MHDQ069:mhcob%0:cob2chR:
64 CHAPTER R A Review of Basic Concepts and Skills R-64
Solution
We can assume the building makes a angle with the ground, and use the
Pythagorean theorem to find the required length. Let c represent this length.
Pythagorean theorem
substitute 9 for a and 27 for b
add
definition of square root;
exact form:
approximate form
The ladder must be at least 28.5 ft tall.
Now try Exercises 51 and 52
c 28.5 ft
2810 281
#
10 9210 c 9210
c 7 0 c 2810
c
2
810
9
2
81, 27
2
729 c
2
81 729
c
2
192
2
1272
2
c
2
a
2
b
2
90°
9 ft
c
27 ft
F. You’ve just reviewed
how to evaluate formulas
involving radicals
R.6 EXERCISES
CONCEPTS AND VOCABULARY
Fill in each blank with the appropriate word or phrase.
Carefully reread the section, if necessary.
1. if is a(n) integer.
2. The conjugate of is .
3. By decomposing the rational exponent, we can
rewrite as
4. is an example of the
property of exponents.
1x
3
2
2
2
3
x
3
2
#
2
3
x
1
116
?
?
2
?
.16
3
4
2 23
n 7 01
n
a
n
a
5. Discuss/Explain what it means when we say an
expression like has been written in simplest
form.
6. Discuss/Explain why it would be easier to simplify
the expression given using rational exponents
rather than radicals:
x
1
2
x
1
3
1A
DEVELOPING YOUR SKILLS
Evaluate the expression for the values given.
7. a. b.
8. a. b.
Simplify each expression, assuming that variables can
represent any real number.
9. a. b.
c. d.
10. a. b.
c. d. 24a
2
12a 92v
10
21y 22
2
225n
2
2x
2
6x 9281m
4
21x 32
2
249p
2
x 8x 7
x 10x 9
2x
2
11. a. b.
c. d.
12. a. b.
c. d.
13. a. b.
c. d.
e. f. 2
6
1h 22
6
2
5
1k 32
5
2
5
243x
5
2
5
243x
10
1
6
641
6
64
B
3
w
3
64
2
3
27q
9
2
3
125p
3
1
3
8
B
3
v
3
8
2
3
216z
12
2
3
125x
3
1
3
64
College Algebra—
cob19413_chR_001-072.qxd 14/10/2008 12:08 PM Page 64 EPG 204:MHDQ069:mhcob%0:cob2chR:

14. a. b.
c. d.
e. f.
15. a. b.
c. d.
16. a. b.
c. d.
17. a. b.
c. d.
18. a. b.
c. d.
19. a. b.
c. d.
20. a. b.
c. d.
Use properties of exponents to simplify. Answer in
exponential form without negative exponents.
21. a. b.
22. a. b.
Simplify each expression. Assume all variables represent
non-negative real numbers.
23. a. b.
c. d.
e. f.
27 272
6
6 228
2
232p
3
q
6
3
8
2
3
64m
3
n
5
22
3
125p
3
q
7
218m
2
A
2x
1
4
y
3
4
B
4
a
24x
3
8
4x
1
2
b
2
a
8y
3
4
64y
3
2
b
1
3
A
2n
2
p
2
5
B
5
a
x
9
8
b
4
3
11252
2
3
a
49
36
b
3
2
100
3
2
a
27x
3
64
b
4
3
1272
2
3
a
4
25
b
3
2
144
3
2
a
125v
9
27w
6
b
2
3
a
16
81
b
3
4
a
4
9
b
3
2
9
3
2
a
27p
6
8q
3
b
2
3
a
4
25
b
3
2
a
16
25
b
3
2
8
2
3
B
25x
6
4
2121
2
4
16m
24
1
3
216
B
49v
10
36
236
2
4
81n
12
1
3
125
2
6
1p 42
6
2
5
1q 92
5
2
5
1024z
20
2
5
1024z
15
1
4
2161
4
216
24. a. b.
c. d.
e. f.
25. a. b.
c. d.
26. a. b.
c. d.
27. a. b.
c. d.
28. a. b.
c. d.
29. a. b.
c. d.
e.
30. a. b.
c. d.
e.
Simplify and add (if possible).
31. a.
b.
c.
d.
32. a.
b.
c.
d. 3240q
9210q
3212x 5275x
5212 2227
3280 22125
2228p 3263p
7218m 250m
8248 32108
12272 9298
1
3
c1
4
c
1
3
3
2
4
3
32
4
a
a2
5
a
6
2
4
81a
12
b
16
2b1
4
b
1
3
6
26
3
4
1
3
b
x2
4
x
5
2
5
32x
10
y
15
9
A
3
125
27x
6
B
20
4x
4
2
3
72b
5
2
3
3b
2
227y
7
23y
12
A
3
81
8z
9
B
45
16x
2
2
3
108n
4
2
3
4n
28m
5
22m
2
3
5cd
2
1
3
25cd
B
ab
2
3 B
25ab
4
27
4
5
25q220q
3
5.122p232p
5
2
3
9v
2
u2
3
3u
5
v
2
B
x
3
y
3 B
4x
5
y
12y
2
3
23b212b
2
2.5218a22a
3
20 232
4
12 248
8
254m
6
n
8
2
9
2
3
27a
2
b
6
32
3
128a
4
b
2
28x
6
R-65 Section R.6 Radicals and Rational Exponents 65
College Algebra—
cob19413_chR_001-072.qxd 14/10/2008 12:08 PM Page 65 EPG 204:MHDQ069:mhcob%0:cob2chR:

33. a.
b.
c.
34. a.
b.
c.
Compute each product and simplify the result.
35. a. b.
c. d.
36. a. b.
c. d.
37. a.
b.
c.
38. a.
b.
c.
Use a substitution to verify the solutions to the
quadratic equation given.
39.
a. b.
40.
a. b. x 5 17
x 5 17
x
2
10x 18 0
x 2 13
x 2 13
x
2
4x 1 0
1315
41221115 162
113
1221110 1112
15 4110
211 21102
1212
616213110 172
115
1142112 1132
13 217
213 2172
12 15
2
2
14 13214 132
15
116 12210.3152
2
16 132
2
1n 1521n 152
13
115 17217122
2
275r
3
132 127r 138
110b 1200b 120 140
52
3
54m
3
2m2
3
16m
3
272x
3
150 17x 127
14 13x 112x 145
3x1
3
54x 52
3
16x
4
41.
a. b.
42.
a. b.
Rationalize each expression by building perfect nth root
factors for each denominator. Assume all variables
represent positive quantities.
43. a. b.
c. d. e.
44. a. b.
c. d. e.
Simplify the following expressions by rationalizing the
denominators. Where possible, state results in exact
form and approximate form, rounded to hundredths.
45. a. b.
46. a. b.
47. a. b.
48. a. b.
1 16
5 213
1 12
16 114
7 16
3 312
110 3
13 12
12
1x 13
7
17 3
6
1x 12
8
3 111
8
31
3
5
A
3
3
2m
2
B
5
12x
B
125
12n
3
4
120
5
1
3
a
A
3
1
4pB
27
50b
B
20
27x
3
3
112
x 7 215x 7 215
x
2
14x 29 0
x 1 110
x 1 110
x
2
2x 9 0
66 CHAPTER R A Review of Basic Concepts and Skills R-66
WORKING WITH FORMULAS
49. Fish length to weight relationship:
The length to weight relationship of a female
Pacific halibut can be approximated by the formula
shown, where W is the weight in pounds and L is
the length in feet. A fisherman lands a halibut that
weighs Approximate the length of the fish
(round to two decimal places).
400 lb.
L 1.131W2
1
3
50. Timing a falling object:
The time it takes an object to fall a certain distance
is given by the formula shown, where t is the time
in seconds and s is the distance the object has
fallen. Approximate the time it takes an object to
hit the ground, if it is dropped from the top of a
building that is in height (round to
hundredths).
80 ft
t
1s
4
College Algebra—
cob19413_chR_001-072.qxd 14/10/2008 12:08 PM Page 66 EPG 204:MHDQ069:mhcob%0:cob2chR:

R-67 Section R.6 Radicals and Rational Exponents 67
APPLICATIONS
51. Length of a cable: A radio tower
is secured by cables that are
anchored in the ground 8 m from
its base. If the cables are attached
to the tower 24 m above the
ground, what is the length of each
cable? Answer in (a) exact form
using radicals, and (b) approximate
form by rounding to one decimal
place.
52. Height of a kite: Benjamin
Franklin is flying his kite in a storm once again.
John Adams has walked to a position directly under
the kite and is 75 m from Ben. If the kite is 50 m
above John Adams’ head, how much string S has
Ben let out? Answer in (a) exact form using
radicals, and (b) approximate form by rounding to
one decimal place.
The time T (in days) required for a planet to make one
revolution around the sun is modeled by the function
where R is the maximum radius of the
planet’s orbit (in millions of miles). This is known as
Kepler’s third law of planetary motion. Use the equation
given to approximate the number of days required for
one complete orbit of each planet, given its maximum
orbital radius.
53. a. Earth: 93 million mi
b. Mars: 142 million mi
c. Mercury: 36 million mi
54. a. Venus: 67 million mi
b. Jupiter: 480 million mi
c. Saturn: 890 million mi
55. Accident investigation: After an accident, police
officers will try to determine the approximate
velocity V that a car was traveling using the
formula where L is the length of the
skid marks in feet and V is the velocity in miles
V 226L
,
T 0.407R
3
2
,
S
75 m
50 m
per hour. (a) If the skid marks were 54 ft long,
how fast was the car traveling? (b) Approximate
the speed of the car if the skid marks were 90 ft
long.
56. Wind-powered energy: If a wind-powered
generator is delivering P units of power, the
velocity V of the wind (in miles per hour) can be
determined using where k is a constant
that depends on the size and efficiency of the
generator. Rationalize the radical expression and
use the new version to find the velocity of the wind
if and the generator is putting out 13.5
units of power.
57. Surface area: The lateral surface
area (surface area excluding the base)
S of a cone is given by the formula
where r is the
radius of the base and h is the height
of the cone. Find the surface area of a
cone that has a radius of 6 m and a height of 10 m.
Answer in simplest form.
58. Surface area: The lateral surface
area S of a frustum (a truncated
cone) is given by the formula
where a is the radius of the upper
base, b is the radius of the lower
base, and h is the height. Find the surface area of a
frustum where and
Answer in simplest form.
h 10 m.b 8 m,a 6 m,
S 1a b22h
2
1b a2
2
,
h
a
b
S r2r
2
h
2
,
h
r
k 0.004
V
A
3
P
k
,
College Algebra—
c
24 m
8 m
cob19413_chR_001-072.qxd 14/10/2008 12:08 PM Page 67 EPG 204:MHDQ069:mhcob%0:cob2chR:
The expression is not factorable using integer
values. But the expression can be written in the form
enabling us to factor it as a “binomial” and
its conjugate: Use this idea to
factor the following expressions.
1x 27
21x 272.
x
2
1272
2
,
x
2
7
59. a. b.
60. a. b. 9w
2
114v
2
11
n
2
19x
2
5
68 CHAPTER R A Review of Basic Concepts and Skills R-68
EXTENDING THE CONCEPT
61. The following terms . . .
form a pattern that continues until the sixth term is
found. (a) Compute the sum of all six terms;
(b) develop a system (investigate the pattern
further) that will enable you to find the sum of 12
such terms without actually writing out the terms.
62. Find a quick way to simplify the expression
without the aid of a calculator.
a3
5
6
b
3
2
4
5
3
4
2
5
10
3
227x 23x 29x
63. If find the value of
64. Rewrite by rationalizing the numerator:
1x h
1x
h
x
1
2
x
1
2
.
A
x
1
2
x
1
2
B
2
9
2
,
aaa
a
aaa
a
OVERVIEW OF CHAPTER R
Important Definitions, Properties, Formulas, and Relationships
R.1 Notation and Relations
concept notation description example
• Set notation: {members} braces enclose the members of a set set of even whole numbers
• Is an element of indicates membership in a set
• Empty set Ø or { } a set having no elements odd numbers in A
• Is a proper subset of indicates the elements of one set
are entirely contained in another
• Defining a set the set of all x, such that x . . .
R.1 Sets of Numbers
• Natural: • Whole:
• Integers: • Rational:
• Irrational: {numbers with a nonterminating, • Real: {all rational and irrational numbers}
nonrepeating decimal form}
R.1 Absolute Value of a Number R.1 Distance between a and b on a
number line
or
b a
a b
0n0 e
n if n 0
n if n 6 0
e
p
q
, where p, q ; q 0f 5. . . , 3, 2, 1, 0, 1, 2, 3, . . .6
50, 1, 2, 3, p6 51, 2, 3, 4, p6
S 5x
|
x 6n for n 65x
|
x . . .6
S ( A
S 50, 6, 12, 18, 24, p6(
14 A
A 50, 2, 4, 6, 8, p6
College Algebra—
cob19413_chR_001-072.qxd 14/10/2008 12:08 PM Page 68 EPG 204:MHDQ069:mhcob%0:cob2chR:

R.2 Properties of Real Numbers: For real numbers a, b, and c,
Commutative Property Associative Property
• Addition: • Addition:
• Multiplication: • Multiplication:
Identities Inverses
• Additive: • Additive:
• Multiplicative:
• Multiplicative:
R.3 Properties of Exponents: For real numbers a and b, and integers m, n, and p
(excluding 0 raised to a nonpositive power),
p
q
#
q
p
1; p, q 0
1
#
a a
a 1a2 00 a a
1a
#
b2
#
c a
#
1b
#
c2a
#
b b
#
a
1a b2 c a 1b c2a b b a
R-69 Overview of Chapter R 69
• Product property:
• Product to a power:
• Quotient property:
• Negative exponents:
1a, b 02
b
n
1
b
n
; a
a
b
b
n
a
b
a
b
n
b
m
b
n
b
mn
1b 02
1a
m
b
n
2
p
a
mp
#
b
np
b
m
#
b
n
b
mn
• Power property:
• Quotient to a power:
• Zero exponents:
• Scientific notation: N 10
k
; 1
N
6 10, k
b
0
1 1b 02
a
a
m
b
n
b
p
a
mp
b
np
1b 02
1b
m
2
n
b
mn
R.3 Special Products
••
•
•
R.4 Special Factorizations
••
••
R.5 Rational Expressions: For polynomials P, Q, R, and S with no denominator of zero,
• Lowest terms: • Equivalence:
• Multiplication: • Division:
• Addition: • Subtraction:
• Addition/subtraction with unlike denominators:
1. Find the LCD of all rational expressions.
2. Build equivalent expressions using LCD.
3. Add/subtract numerators as indicated.
4. Write the result in lowest terms.
R.6 Properties of Radicals
• is a real number only for
• only if
• For any real number a, when n is even1
n
a
n
a
b
n
a1
n
a b,
a 01a
P
R
Q
R
P Q
R
P
R
Q
R
P Q
R
P
Q
R
S
P
Q
#
S
R
PS
QR
P
Q
#
R
S
P
#
R
Q
#
S
PR
QS
P
Q
P
#
R
Q
#
R
P
#
R
Q
#
R
P
Q
A
3
B
3
1A B21A
2
AB B
2
2A
3
B
3
1A B21A
2
AB B
2
2
A
2
2AB B
2
1A B2
2
A
2
B
2
1A B21A B2
1A B21A
2
AB B
2
2 A
3
B
3
1A B21A
2
AB B
2
2 A
3
B
3
1A B2
2
A
2
2AB B
2
1A B2
2
A
2
2AB B
2
; 1A B21A B2 A
2
B
2
College Algebra—
• only if
• If n is even, represents a real number only
if
• For any real number a, when n is odd1
n
a
n
a
a 0
1
n
a
b
2
a2a b,
cob19413_chR_001-072.qxd 14/10/2008 12:08 PM Page 69 EPG 204:MHDQ069:mhcob%0:cob2chR:
