Чупров И.Ф., Канева Е.А., Мордвинов А.А. Уравнения математической физики с приложениями к задачам нефтедобычи и трубопроводного транспорта газа

Подождите немного. Документ загружается.

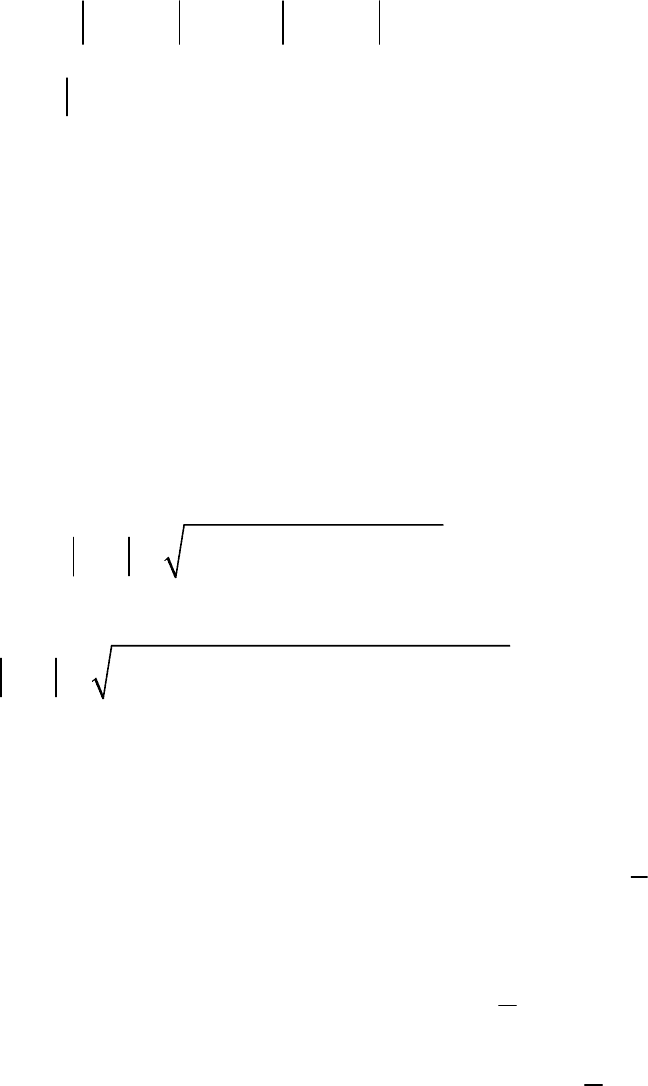
111

(

)

()

(

)

,max,

xy Г

uxy uxy

∈

≤

В частности, если

u =

, то

(

)

,0вuxy D

≡

Из принципа максимума следуют и многие другие важные свойства гар-

монических функций.

Отметим, что теорема о среднем и принцип максимума выполняются и

для функций, гармонических в пространственных областях.

§ 4. Функция Грина

Рассмотрим уравнение Лапласа

∆

на плоскости или в пространстве

в области

D. Рассмотрим точки

(

)

,pxy и

(

)

000

,pxy для плоскости и

(

)

,,pxyz и для пространства. Расстояния между этими точками

будут

(

000

,,px y z

)

()()

rpp xx yy==−+−

или

()()()

000

rpp xx

zz==−+−+−.

Пусть на границе области задано нулевое значение функции (нулевое ус-

ловие Дирихле).

Определение. Функция

(

)

,Gpp называется функцией Грина задачи Ди-

рихле в области

D, если для любой фиксированной точки

D∈

, она, как

функция от

, удовлетворяет следующим условиям: 1) непрерывная в

D всю-

ду, кроме точки

(

)

,Gpp 0

на границе ; 2) гармоническая в за

исключением точки

D D

; 3) в случае плоскости

()

,lnGpp

−

остается гармо-

нической функцией в точке

; в случае пространства

()

,Gpp

−

остается

гармонической в точке

Функцию Грина называют также функцией источника. Функция Грина

(

)

,Gpp (если она существует) однозначно определяется условиями 1-3. Кро-

ме того

(

)

,Gpp > 0 в области . D

Задача 1. Построить функцию Грина для плоской области, ограниченной

кругом.

Введем понятие сопряженных точек относительно окружности.

112

Определение. Точки

и называются сопряженными относительно

окружности, если они лежат на одном луче, исходящем из центра

О окружно-

сти, и произведение их расстояний от центра равно квадрату радиуса:

*Op Op R⋅=

(рис. 5.2).

Рис. 5.2

Обозначим через

rOp= и *rOp*

. Тогда

*rr R

⋅

= . Так как точ-

ки

и лежат на одном луче, выходящем из начала координат, то

0000 0 0

***

*,*

xyrR R R

xyrr r r

===⇒=⋅ =⋅

Возьмем функцию

()

,lnln

Gpp

=−

⋅

, (5.5)

где

rpp= ,

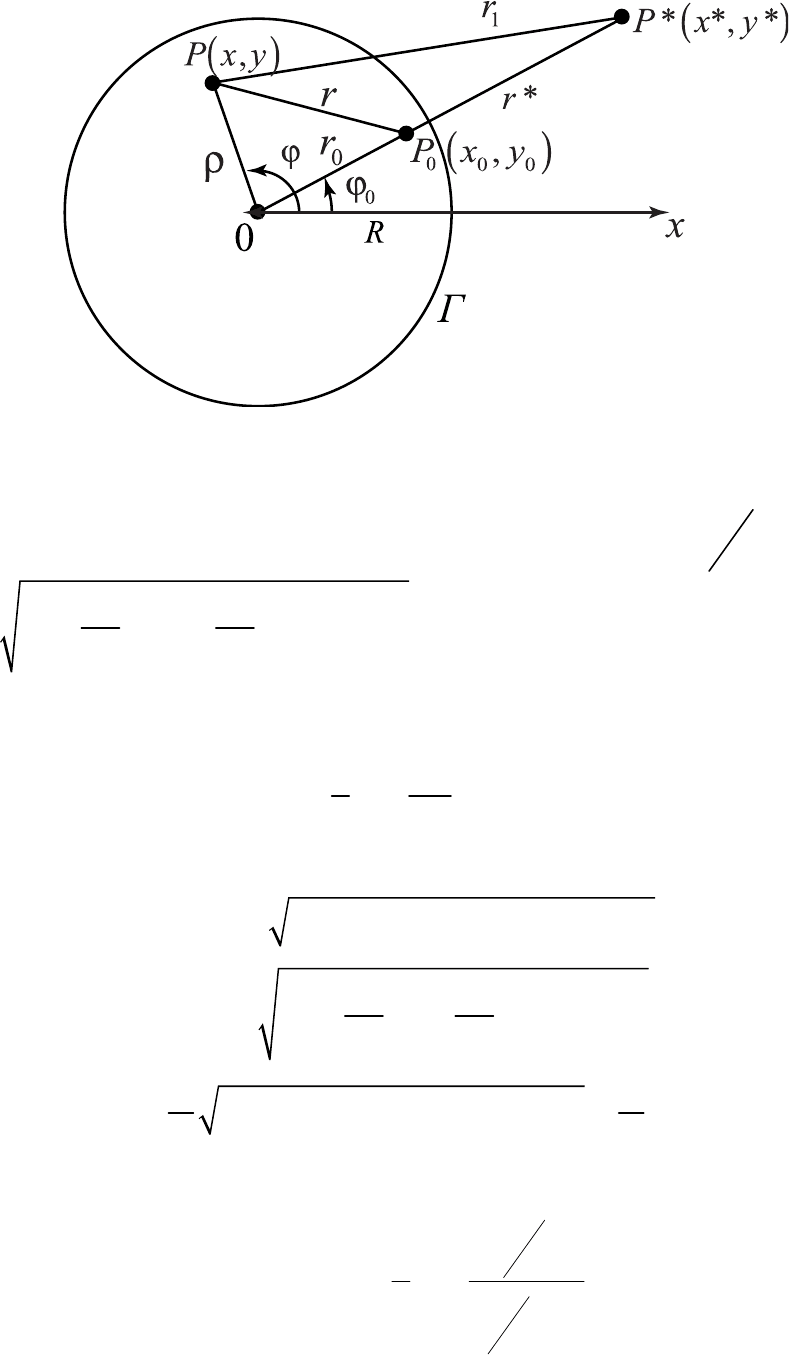
*rpp= (рис. 5.3).

Из треугольника

по теореме косинусов

()

2cosrrr=ρ+ −ρ⋅⋅ ϕ−ϕ

()

*2 *rrr=ρ+ −ρ⋅ ⋅ϕ−ϕ

113

Рис. 5.3

Воспользовавшись равенством

rr R r

⋅= ⇒= , получим

()

2cos

=ρ+ −⋅ρ⋅ ϕ−ϕ r. Величины и выражаются через

rρ

и ,

, в конечном счете через

,,, ,

xyx y

Покажем, что (5.5) удовлетворяет условиям 1-3 определения функции

Грина. Функция

()

,lnln

Gpp

=−

непрерывна в круге кроме точки

(когда

). На границе круга

0r =

()

2cos

rRrRr

ρ=

=−−⋅⋅ϕ−ϕ

()

00 0

2cos

rR R

Rr Rr r

ρ=

=+− ϕ−ϕ=

=−−⋅⋅ϕ−ϕ=⋅

Отсюда

()

,lnln

Gpp

−=

⎛⎞

⋅

⎜⎟

⎝⎠

т.е. на границе обращается в нуль.

114

Функция

(

)

,Gpp гармоническая в за исключением точки D

, что

можно проверить, если записать оператор Лапласа в полярной системе коорди-

нат с полюсом в точке

Выполняется и третье условие. Функция

()

,lnln

Gpp

−=−

бу-

дет гармонической в точке

, т.к. принадлежит области , а точка лежит

вне области

и .

0r >

Примечание. Аналогично строится функция Грина для шара радиуса R.

Она имеет вид

()

Gpp

=−

, (5.6)

где

rpp= ,

*rpp= ,

rOp=

. Точка в этом случае – сопряженная

точка

относительно сферы радиуса R c центром в точке О, т.е.

*Op Op R⋅=

Функцию Грина можно рассматривать не только для ограниченных, но и

для неограниченных областей.

Задача 2. Построить функцию Грина для полуплоскости.

Определим точки, сопряженные относительно прямой. Точки

называются сопряженными относительно прямой, если они симметричны отно-

сительно этой прямой (рис.5.4а).

а) б)

Рис. 5.4

Функция

()

,lnlnGpp

=−

, (5.6)

115

где

()()

rpp xx yy==−+−

()()

*rpp xx yy==−++

(рис.5.4б) удовлетворят свойствам 1-3 определения функции Грина в полуплос-

кости

. В самом деле, на границе области при

0y > 0y

, поэтому

rr=

(

)

Gpp

= 0. Гармоничность функции

в области проверим не-

посредственно

0y >

111 11

111

ln ln

drd

xr dr rdx rr

⎛⎞ ⎛⎞

−

∂

=⋅=−⋅

⎜⎟ ⎜⎟

∂

⎝⎠ ⎝⎠

;

111

yr r r

⎛⎞

∂

=− ⋅

⎜⎟

∂

⎝⎠

;

(

)

11 1

xrr r r

−

⎛⎞

∂

⋅−

⎜⎟

∂

⎝⎠

;

(

)

11 1

yrr r

⎛⎞

∂

⋅−

⎜⎟

∂

⎝⎠

;

ln 0

⎛⎞

∆

⎜⎟

⎝⎠

Следовательно, функция

(

)

,Gpp гармоническая в области всю-

ду, кроме точки

0y >

, а

()

,lnlnGpp

−=−

гармоническая в точке

Примечание. Для полупространства

функция Грина имеет вид

0z >

()

,Gpp

−

где

()()()

rxx

zz=−+−+−,

()()()

10 0

rxx yy zz=−+−++

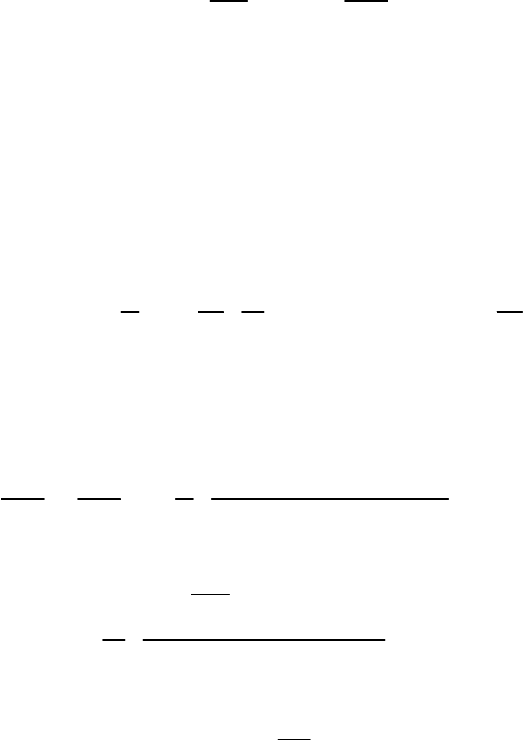
116

§ 5. Решение задачи Дирихле методом функции Грина

Главная задача математической физики – построение решения данного

дифференциального уравнения в частных производных, удовлетворяющего за-

данными граничным и начальным условиям. Метод Фурье использует технику

разложения искомого решения по собственным функциям. Этот метод приво-

дит к цели, если только удается найти подходящую для заданных границ сис-

тему координат, допускающую разделение переменных в уравнении

. Однако

есть множество задач, где такое разделение не удается, т.к. граница тела доста-

точно сложна.

Если же метод Фурье применим, результат обычно получается в виде ря-

да, который часто сходится медленно, что затрудняет анализ решения.

Для некоторых видов задач желательно иметь решение в замкнутой фор-

ме, хотя бы в

форме интеграла. Использование функций Грина представляет

такой подход. Метод функции Грина решения задачи Дирихле основывается на

формулах Грина. Оставляя в сторону выводы, напишем формулу, которая дает

решение задачи Дирихле на плоскости, если известна функция Грина

() ()

ux y f s d

∂

=−

π∂

∫





. (5.7)

Здесь

Г – граница области (ориентирована положительно),

()

s – ус-

ловие на границе. Производная от функции

G берется по внешней нормали к

границе.

Построим решение задачи Дирихле для круга. Функция

(

)

,Gpp для

этого круга имеет вид

()

01 0

,lnln lnlnln

Gpp r r

rrr

=−⋅=−+−

Так как направление внешней нормали совпадает с направлением поляр-

ного радиуса

(рис. 5.3), то

(

)

()

cos

nrr

−⋅ ϕ−ϕ

∂∂

==−⋅

∂∂ρ

ρ− ϕ−ϕ

+⋅

На границе

Г расстояние

, поэтому

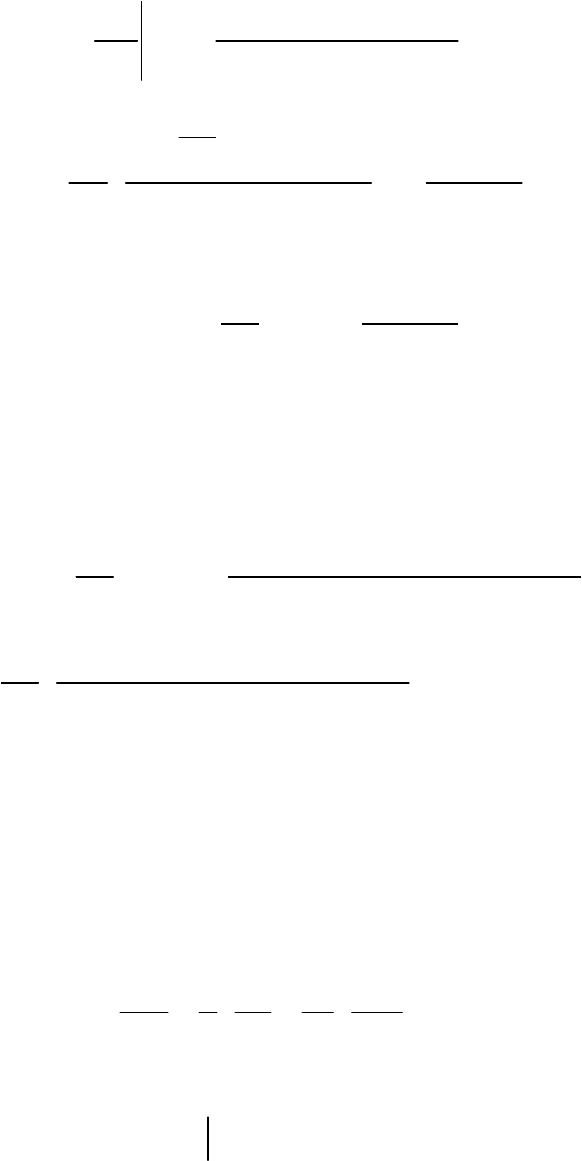
117

(

)

()

cos

rr R

Rr R

−⋅ ϕ−ϕ

∂

=− +

∂

−ϕ−ϕ

−

+⋅ =−

Подставим полученное выражение для производной в формулу (5.7)

() ()

ux y f s d

−

=⋅

∫



)

(5.8)

Так как точка

может быть произвольной внутри круга, обо-

значим ее координаты

(

000

,pxy

cosx =ρ α

siny

ρα

(

)

α – полярная система

координат с полюсом в точке

О. Тогда (5.8) примет вид

() ()

()

22cos

−ρ

ρα = ϕ ⋅ ϕ

π − ⋅ρ⋅ ϕ−α +ρ

∫

. (5.9)

Функция

()

22cos

−ρ

⋅

π − ⋅ρ⋅ ϕ−α +ρ

называется ядром Пуассона

для круга.

§ 6. Задача Дирихле для круга. Решение методом Фурье

Найдем методом Фурье решение задачи Дирихле для круга. Радиус круга

обозначим через

, центр поместим в начало координат. Очевидно, что здесь

необходимо решать задачу в полярных координатах

uu u

rrrr

∂∂∂

+⋅ + ⋅ =

∂∂∂ϕ

. (5.10)

На границе круга задано условие первого рода

()

(

)

(

)

ur uR f

ϕ= ϕ=ϕ, (5.11)

где

(

)

f ϕ – заданная функция.

Обратим внимание на постановку краевой задачи: здесь нет начальных

условий. Это и понятно – ведь рассматривается установившийся процесс, кото-

рый от времени не зависит.

Следуя идее метода разделения переменных, будем искать решение зада-

чи в виде

(

)

(

)

(

)

,ur Rr Фϕ= ⋅ ϕ≠0. (5.12)

118

Подставим искомое решение в уравнение

"' "R Ф R Ф R Ф

+⋅ + ⋅ =0

. (5.13)

Разделим переменные и приравняем обе части числу

""rR Ф

R Ф

−=λ.

(Ниже дано обоснование такого обозначения). Если решение задачи ис-

кать в форме (5.12), то уравнение распадается на два обыкновенных дифферен-

циальных уравнения

"ФФ0

λ=

, (5.14)

"'rR rR R 0

−λ =

. (5.15)

Решение уравнения (5.14)

. (5.16)

()

cos sinФА Bϕ= ⋅ λϕ+ ⋅ λϕ

Покажем, что

не может принимать произвольные значения. Действи-

тельно, искомая функция

(

)

,ur

является периодической относительно

периодом

2π

(

)

(

)

,2 ,ur ur

+π= ϕ. Это вытекает из характера полярной

системы координат: увеличение

на

возвращает точку

(

)

,r ϕ в исходное

положение. Но тогда и функция

(

)

, как показывает (5.12), должна обладать

свойством периодичности. Последний вывод и позволяет определить

, т.к.

должно выполняться

()

(

)

cos 2 sin 2 cos sinABA⋅ λ ϕ+ π + ⋅ λ ϕ+ π ≡ ⋅ λϕ+ λϕB

или

()

(

)

cos 2 sin 2 cos sinABA⋅ λϕ+ πλ + ⋅ λϕ+ πλ ≡ ⋅ λϕ+ λϕB

Последнее тождество выполняется только тогда, когда

есть целое чис-

ло,

– собственные числа задачи

nλ=

(

)

∈

. Отрицательные можем от-

бросить, т.к. знак

влияет только на знак произвольной постоянной .

Равенство (5.16) сейчас можно переписать в виде

. (5.17)

()

cos sinФ AnBnϕ= ⋅ ϕ+ ⋅ ϕ

Перейдем теперь к решению уравнения (5.15)

RR R

−=. (5.18)

119

Это уравнение второго порядка имеет переменные коэффициенты при

неизвестной функции и ее производной, поэтому метод интегрирования линей-

ных уравнений здесь не применим. Будем искать решение этого уравнения, на-

зываемого уравнением Эйлера, в виде

(

)

. (5.19)

После подстановки этого соотношения в уравнение получим

()

2212

rnn r rnr r

−−

⋅−⋅+⋅⋅−λ⋅=

или

(

)

10nn n

−

+−λ=,

или

(

)

0; 0nn−λ = =±λ λ≥

Общее решение уравнения Эйлера будет

()

rcrDr

−

⋅+⋅

. (5.20)

Рассмотрим случай

, т.е.

0n = 0

. Уравнения (5.14) и (5.15) примут

вид

"0ФФAB=⇒ = + ϕ

"'0 lrR rR Rc D r⋅+⋅=⇒=+ ⋅n

Так как решение должно быть периодическим с периодом

, то

2π

должно равняться нулю. Кроме того, в силу ограниченности решения всюду

внутри круга, в том числе и в центре

(

)

, должно равняться нулю. От-

сюда делаем вывод – нулевое решение должно быть постоянным (постоянная

функция является периодической функцией любого периода). Обозначим это

решение

В решение (5.20) надо положить

. Иначе функция в центре круга

обратится в бесконечность и искомое решение не будет ограниченным. Тогда

()

rcr=⋅

в силу линейности и однородности уравнения Лапласа решение

будет

() (

,coss

ur A n B n r

∞

ϕ= + ⋅ ϕ+ ⋅ ϕ

∑

)

. (5.21)

Здесь

;

Ac A⋅=

cB⋅=

Коэффициенты полученного ряда Фурье подберем так, чтобы решение

удовлетворяло краевому условию (5.11)

120

() ()

cos sin

uf AnBn

∞

=ϕ= + ⋅ ϕ+⋅ ϕ⋅

∑

По известным формулам разложения периодической

(

)

2T =π функции в

полный ряд Фурье находим коэффициенты

()

−π

ϕϕ

∫

;

()

cos

−π

=ϕ⋅

⋅π

∫

dϕϕ;

()

sin

−π

=ϕ⋅

⋅π

∫

ndϕϕ.

После подстановки найденных коэффициентов можно решение предста-

вить в виде

() () ()

()

sin sin .

ur f d f d n

fndn

∞

−π

⎛

ϕ= τ τ+ τ⋅ ττ⋅ ϕ+

⎜

ππ

⎝

⎞

⎛⎞

+τ⋅τ⋅τ⋅ϕ⋅

⎟

⎜⎟

⎝⎠

⎠

∑

∫

oscos

(5.22)

Этот ряд является сходящимся к функции

(

)

,ur

при условии непре-

рывности и дифференцируемости функции

(

)

Запишем решение (5.22) в другой форме. Меняя порядок суммирования и

интегрирования, получим

() () (

)

() ()

,cos

sin sin 1 cos .

ur f n n

nnd f n d

∞

−π

∞

−π

⎛⎞

ϕ= τ + ⋅ ϕ⋅ τ+

⎜⎟

⎝⎠

⎛⎞

+ϕ⋅ττ= τ+ ϕ−τ

⎜⎟

⎝⎠

∑

∫

∑

∫

cos

По формуле Эйлера

() ()

()

cos exp exp

nininϕ−τ = ϕ−τ + − ϕ−τ

Обозначим