Чупров И.Ф., Канева Е.А., Мордвинов А.А. Уравнения математической физики с приложениями к задачам нефтедобычи и трубопроводного транспорта газа
Подождите немного. Документ загружается.

61
и постоянных граничных условиях
0
,.
H
k
xx
uuuu
==
=
=
Рассмотрим функцию
() ()
,,
kH
H
uu
vxt uxt u x
−
⎡
⎤
=−+
⎢
⎥
⎣
⎦
. (3.25)
Видим, что
0
0
xx
vv
==
=
=
,
() ()
0
kH
H
t
uu
vfxu x
=
x
−
⎛⎞
=−+ =ϕ
⎜⎟
⎝⎠
.
Пусть
(
)
,vxt является решением уравнения
2
2
2
vv
a
tx
∂
∂
=
∂
∂
,
при начальном условии
(
)
0t
vx
=
=
ϕ
и нулевых граничных условиях.
Функция
(
)
,vxt может быть найдена согласно (3.21). Тогда искомая
функция
(
)
,uxt найдется из (3.25).
Окончательное решение задачи примет вид:
() (
,
kH
H
uu
uxt u x vxt
)
,
−
=+ +
. (3.26)
Приведем примеры на применение метода Фурье для уравнения тепло-
проводности при условии, что рассматриваемая область конечна.
Пример 1. Решить уравнение
2
2
9
uu
tx
∂
∂
=
∂
∂
,
[
]
0,1x
∈
,
[
]
0,t ∈∞ при на-
чальном условии
и граничных условиях
.
()
32
,0 4sin sinux x x=π−π
() ()
0, 1, 0utut==
Здесь нулевые граничные условия. Можно сразу применить метод Фурье.
Согласно формуле (3.21) решение задачи будет
() ( )
(
)
2
1
,exp3sin
n
n
uxt A n t nx
∞
=
=−π⋅
∑
π
, (3.27)

62
где
()
1
3
0
2 4sin sin 2 sin
n
A
xxn=π−π⋅
∫
xdxπ.
Выполним преобразования начального условия
()
(
)
32
4sin sin 2 4sin 1 cos sin 2
1cos2
4sin 1 sin 2
2
2sin 2sin cos 2 sin 2
2sin sin 3 sin sin 2 3sin sin3 sin 2 .
fx x x x x x
x
xx
xxxx
xxxx xx
= π−π=π−π−π=
+π
⎛⎞
=π− −π=
⎜⎟
⎝⎠
=π−π⋅π−π=
= π−π+π−π=π−π−π
x
x
Вычислим коэффициент ряда
.
n
A
()
1
0
111
000
2 3sin sin3 sin 2 sin
6 sin sin 2 sin 3 sin 2 sin 2 sin .
n
Axxxnxdx
xnxdx xnx xnxd
=π−π−π⋅π=
= π⋅π− π⋅π− π⋅π
∫
∫∫∫
Вычислим интегралы.
() ()
()
()
()
()
()
()
()
()
11
1
00
1
0
6sin sin 3 cos 1 cos 1
sin 1 sin 1 sin 1 sin 1
33
11 1
J x n xdx n x n x dx
nx nx n n
nn n n
=π⋅π= −π−+π=
⎛⎞⎛⎞
−π +π −π +π
=−=−
⎜⎟⎜⎟
−π +π −π +
⎝⎠⎝⎠
∫∫
,
1
где
1, 2, 3n = …
Если
, то интеграл равен 0. При
1n ≠ 1n →
(
)
()
1
sin 1
lim 1
1
n
n
n
→
−
π
=
−π
.
Итак,
. Также можно показать, что
1
3J =
1
2
0
1 при 3,
2sin3 sin
0 при 3.
n
Jxnxdx
n
=
⎧
=π⋅π=
⎨
≠
⎩
∫
1
3
0
1 при 2,
2 sin 2 sin
0 при 2.
n
Jxnxdx
n
=
⎧
=π⋅π=
⎨
≠
⎩
∫
Отсюда
,
1
3A =
2
1A
=
−
, ,
3
1A =− 0
n
A
=
при . Подставляя эти коэффи-
циенты в формулу (3.27), получаем
4n ≥

63
()
()
(
)
()
22
2
, 3exp 9 sin exp 36 sin 2
exp 81 sin 3 .
uxt t x t x
tx
=−π⋅π−−π⋅π
−−π⋅π
−
(3.28)
В этом примере ответ получили в виде элементарной функции, что обу-
словлено особенностью начального условия, а именно тем, что
(
)
f
x есть ли-
нейная комбинация функций
sin kx
π
. Легко видеть, что решение (3.28)
удовлетворяет начальному и граничным условиям, а также дифференциальному
уравнению.
Пример 2. Пусть нефтяной пласт, имеющий постоянную температуру
,
начал прогреваться плоской батареей скважин с температурой
0
u
H
u
. На расстоя-
нии
от батареи поддерживается температура . Необходимо исследовать не-
стационарный процесс распространения температуры в зоне пласта при
предположении, что тепло распространяется только с помощью теплопровод-
ной составляющей. Такая постановка задачи физически оправдана при прогреве
призабойной зоны пласта или при густой сетке нагнетательных скважин. Прак-
тически с помощью теплопроводной составляющей прогревается пласт в шахт-
ных уклонах Ярегского
месторождения, разрабатываемого термошахтным
способом, на начальном этапе прогрева пласта. Здесь из-за высоких фильтраци-
онных сопротивлений при густой сетке нагнетательных скважин теплоноситель
в основном прорывается в подстилающий пласт водоносный горизонт.
k
u
Рассмотрим эту задачу применительно к условиям пласта Ярегского ме-
сторождения. Начальная температура пласта 6°. Температура теплоносителя
120°, коэффициент теплопроводности
232 2
3, 5 10 / 31 /a
м
час м год
−
=⋅ ≈
,
длина участка пласта 15 м.
При этих предположениях необходимо решить уравнение
2
2
31
uu
tx
∂
∂
=
∂
∂
,
при начальном условии
(
)
,0 6ux
=
и граничных условиях
(
)
0, 120ut
=
и
(
)
15, 6ut
=
.
Здесь ненулевые граничные условия.
Воспользуемся формулой (3.26).
()
1
6120
, 120 sin
15 15
n
n
n
uxt x A x
∞
=
−
π
=+ + ⋅
∑
,
где

64
()
()
15
0
218
6sin 1 1
15 15
0 при 2,
11,5
при 21.
n
n
n
Axdx
n
nk
nk
n
π
=⋅ =−−
π
=
⎧
⎪
=
⎨
=−
⎪
⎩
∫
=
()
()
()
()
()
(
() ()
2
1
,1207,6
sin 2,1 2 1
11,5 exp 3 2 1
21
120 7,6 11,5 sin 2,1 exp 3
sin 6,3 sin10,5
exp 27 exp 75 .
35
k
uxt x
kx
kt
k
xxt
xx
tt
∞
=
=
−+
−
+⋅−
−
=− + ⋅ −+
⎞
+−+⋅−
⎟
⎠
∑
…
−=
+
(3.29)
При больших значениях
( , единицей измерения времени взят один
год) вместо суммы ряда достаточно взять 1-й член ряда. Расчеты показывают,
что в течение 1 года температурный фронт достигает 14 м. Температура на рас-
стоянии 1 м – 113°, 2 м – 104°, 3 м – 97° и т.д. По формуле (3.29) можно опре-
делить температуру в любой момент времени для любого
t
1t ≥
[
]
0,15x ∈ . Сумма
ряда в (3.29) практически равна нулю при
. Наступает стационарный про-
цесс,
2t ≥
(
)
, 120 7,6ux x∞≈ − .
Пример 3. Пласт, имеющий форму кругового цилиндра радиуса
, имел
температуру
. В момент времени
R
0
u
0t
=
начала работать кольцевая галерея
нагнетательных скважин, расположенных по боковой поверхности пласта. В
результате чего на поверхности поддерживается постоянная температура, кото-
рую будем считать равной условному нулю температуру
(
)
0
0u < . Толщина
пласта такова, что теплопотери в кровлю и подошву отсутствуют. Прогрев
осуществляется теплопроводностью.
При этих предположениях необходимо найти решение уравнения
2
2
2
1uu
a
trr
⎛⎞
∂∂∂
=+⋅
⎜
∂∂∂
⎝⎠
u
r
⎟
, (3.30)
при начальном условии
0
0
t
u
=
u
=
, (3.31)
и граничном условии
0
rR
u
=
=
. (3.32)
65
Отметим еще, что решение существует всюду, в том числе и при
, т.е.
0r =
(
)
0,ut – существует. (3.33)
Согласно метода Фурье будем искать решение уравнения в виде
()
(
)
(
)
,uxt Xr Tt
=
⋅
и подставим в уравнение (3.30).
2
2
2
1
'
dX dX
TX aT
dr r dr
⎛⎞
=+
⎜⎟
⎝⎠
.
Разделим переменные:
2
2
2
1
'
dX dX
T
dr r dr
XaT
+
=
=−λ. (3.34)
Откуда
2
2
1
0
dX dX
X
dr r dr
+
+λ = . (3.35)
Согласно (3.32), (3.33) функция
(
)
Xr должна удовлетворять тем же ус-
ловиям по
, что и искомая функция r
(
)
,urt, т.е.
(
)
0XR
=
. (3.36)
Решением уравнения (3.35) будет функция
()
(
)
0
Xr J r
=
λ
. (3.37)
Подставим (3.37) в (3.36)
(
)
0
0JR
λ
=
.
Отсюда
nn
R
v
λ
=
, где – положительные корни уравнения
n
v
(
)
0
0Jx= .
n
n
v
R
λ
=
. (3.38)
Множество собственных функций
задачи задается формулой X
()
0
n
n
vr
Xr J
R
⎛⎞
=
⎜
⎝⎠
⎟
. (3.39)
66
Будем искать решение задачи в виде ряда
() ()
0
1
,
n
n
n
vr
urt T t J
R
∞
=
⎛⎞
=⋅
⎜
⎝⎠
∑
⎟
. (3.40)
Граничные условия для (3.40) выполняются.
Переходим к определению функции
(
)
n
Tt. Подставим (3.40) в (3.30)
() ( ) ()
2
'2
2
11
1
nn
nn n
nn
dX dX
Tt X r a Tt
dr r dr
∞∞
==
⎛⎞
⋅= +
⎜⎟
⎝⎠
∑∑
.
Но согласно (3.35)
2
2
1
nn
nn
dX dX
X
dr r dr
+
=−λ ⋅ .
Поэтому имеем
() ()
()
()
'2
1
0
nnnn
n
Tt a Tt X r
∞
=
+
λ=
∑
,
или
() ()
22
'
0
2
1
0
nn
nn
n
av vr
Tt Tt J
nR
∞
=
⎛⎞
⎛⎞
+=
⎜⎟
⎜⎟
⎝⎠
⎝⎠
∑
.
Тождественный нуль разложен на отрезке
[
]
0, R по собственным функ-
циям задачи. Поэтому коэффициенты разложения равны нулю
() ()
22
'
2
0
n
nn
av
Tt Tt
R
+
= . (3.41)
Подчиним решение (3.40) начальному условию (3.31)
()
0
00
0
1
0
n
t
n
v
uTJr
R
∞
=
=
⎛⎞
=⋅
⎜⎟
⎝⎠
∑
u
=
.
Из этого соотношения с применением свойства ортогональности функции
Бесселя найдем начальные условия для уравнения (3.41).
()
()
0
1
2
0
n
nn
u
T
vJ v
=
. (3.42)
Тогда решение уравнения (3.41) имеет вид
()
()
2
0
1
2
exp
n
n
nn
uav
Tt t
vJ v R
⎛⎞
⎛⎞
=⋅−
⎜
⎜⎟
⎜
⎝⎠
⎝⎠
⎟
⎟
. (3.43)
67
Окончательно решение задачи будет
()
()
2
0
0
1
1
1
,2 exp
n
n
n
nn
v
J
r
av
R
urt u t
vRJ
∞
=
⎛⎞
⎜⎟
⎛⎞
⎛⎞
⎝
=⋅−⋅
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
∑
v
⎠
. (3.44)
Можно показать, что при
0r
=
этот ряд сходится, поэтому условие (3.33)
выполняется.
§ 6. Неоднородное уравнение теплопроводности
Случай 1. Рассмотрим неоднородное уравнение
(
2
2
2
,
uu
af
tx
∂∂
=+
∂∂
)
xt, (3.45)
с начальным условием
0
0
t
u
=
=
, (3.46)
и с граничными условиями
()
(
)
0, , 0utut
=
= . (3.47)
Будем искать решение задачи в виде
() ()
1
,si
n
n
n
uxt T t x
∞
=
n
π
=⋅
∑
. (3.48)
Решение (3.48) удовлетворяет граничным условиям. Для того чтобы вы-
полнялось начальное условие, необходимо
(
)
0
n
T 0
=
. (3.49)
Пусть функция
(
,
)
f
xt такова, что ее можно разложить в ряд по синусам
() ()
1
,s
n
n
n
in
f
xt t x
∞
=
π
=ϕ ⋅
∑
, (3.50)
где
() ()
0
2
,sin
n
n
tfxt x
π
ϕ= ⋅
∫
dx
. (3.51)
Подставим ряд (3.48) в уравнение (3.45) и учтем (3.50)
() () ()
2
'
1
sin 0
nnn
n
an n
Tt Tt t x
∞
=
⎛⎞
ππ
⎛⎞
+−ϕ
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
∑
=
.
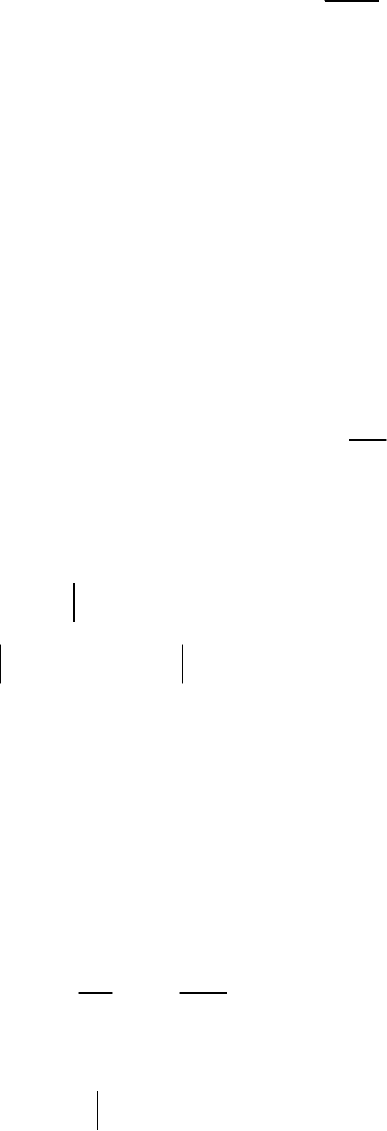
68
Для определения функции
(
)
n
Tt получили линейное дифференциальное
уравнение первого порядка
() () ()
'2
,
nnnn n
an
Tt Tt t
π
⎛⎞
+ω ⋅ =ϕ ω =
⎜
⎝⎠
⎟
, (3.52)
при начальном условии
(
)
00
n
T
=
.
Решая обыкновенное линейное дифференциальное уравнение (3.52) при на-
чальном условии (3.49), находим
()
()
()
2
0
n
t
t
n
Tt e d
−ω −τ
=
⋅ϕ τ τ
∫
. (3.53)
Решение поставленной задачи будет
()
()
()
2
1
0
,
n
t
t
n
n
n
uxt e d x
∞
ω−τ
=
⎛⎞
sin
π
=⋅ϕττ
⎜⎟
⎝⎠
∑
∫
. (3.54)
Случай 2. Неоднородные граничные и начальные условия.
Пусть необходимо найти решение уравнения (3.45) при условиях
(
)
0
0
t
u
=
x
=
=ϕ
, (3.55)
(
)
(
)
1
0
;
xx
utu
==
=ψ =ψ
2
t
. (3.56)
Эту задачу будем в принципе решать так же, как и задачу о вынужденных
колебаниях струны.
Будем искать решение задачи (3.45) при условиях (3.55) и (3.56) в виде
суммы двух функций
(
)
(
)
(
)
,,u xt v xt xt,
=
+ω , (3.57)
где функция
удовлетворяет однородному уравнению v
2
2
2
vv
a
tx
∂
∂
=
∂
∂
, (3.58)
при условиях
(
)
0t
v
=
x
=
ϕ
, (3.59)
()
(
)
(
)
(
)
1
0, ; ,vt tvt t=ψ =ψ
2
, (3.60)
а функция
удовлетворяет неоднородному уравнению
ω
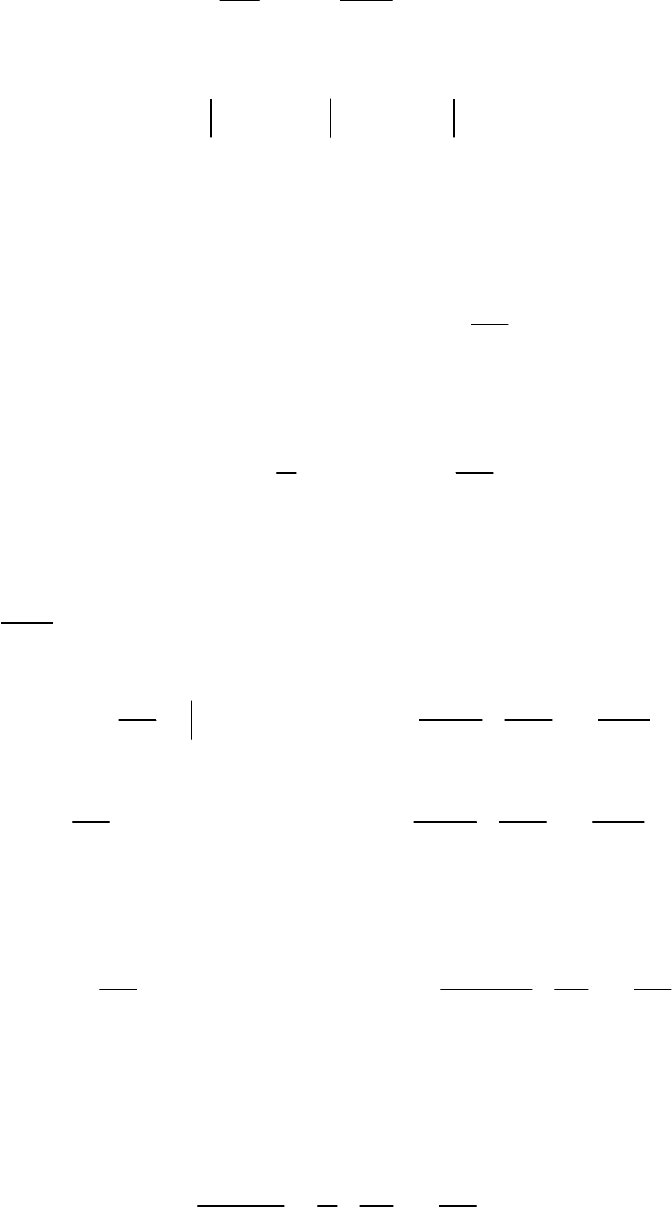
69
(
2
2
2
,af
tx
∂ω ∂ ω
=⋅ +
∂∂
)
xt (3.61)
и условиям
00
0, 0, 0.
txx===
ω=ω=ω=
(3.62)
Эта задача нами уже решена в начале этого параграфа.
Остается найти функцию
(
)
,vxt.
Решение задачи (3.58) ищем в виде ряда
() ()
1
,si
n
n
n
vxt T t x
∞
=
n
π
=⋅
∑
, (3.63)
где
() ()
0
2
,sin
n
n
Tt vxt xdx
π
=⋅
∫
. (3.64)
Интегрируем (3.64) два раза по частям, обозначив
(
)
,uvxt= ,
sin
nx
dV dx
π
=
. Получим
() ()
()
() ( ) ()
()
2
22 2
0
0
2
12
22 2
0
22
1sin
22
1sin
n
nx
x
n
vnx
Tt u u dx
nnx
vnx
tt
nnx
=
=
∂π
=−−−
ππ∂
∂π
=ψ−−ψ −
ππ∂
∫
∫
.
dx
=
(3.65)
С другой стороны, за
можно принять функцию
()
n
Tt
() () ( ) ()
()
12
222
0
22
1
n
n
vn
Tt t t xdx
nan
∂π
=ψ−−ψ −
ππ
∫
sin
t
∂
. (3.66)
Действительно, если приравнять (3.65) и (3.66), то получим уравнение
(3.58).
Дифференцируем выражение (3.64) по
t
()
0
2
sin
n
dT t
vn
xdx
dt t
∂π
=
∂
∫
. (3.67)
Исключим интеграл из равенств (3.66), (3.67). Получим уравнения для
()
n
Tt
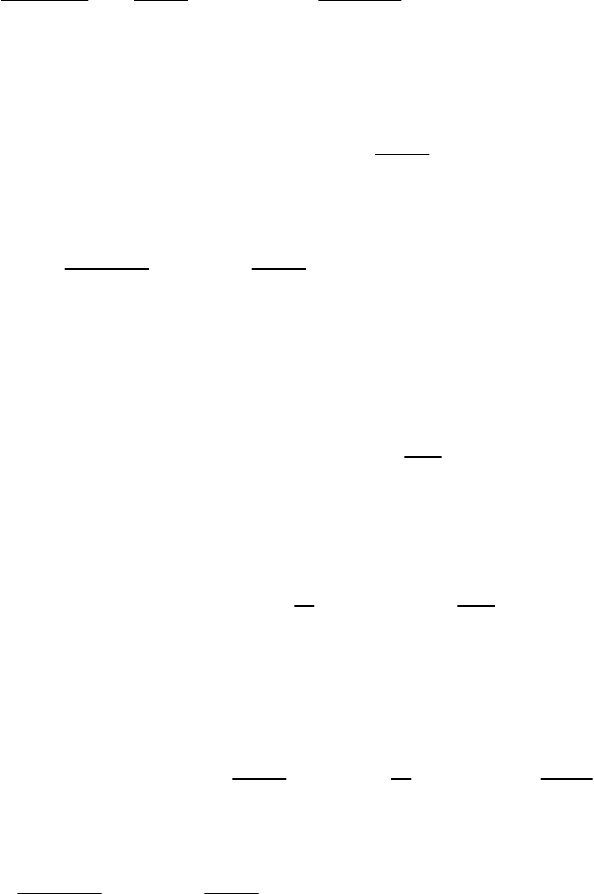
70
()
() () ( )
()
()
2
2
1
2
2
1
n
n
n
dT t
an a n
Tt t t
dt
ππ
⎛⎞
+=ψ−−
⎜⎟
⎝⎠
2
ψ
. (3.68)
Общее решение этого уравнения имеет вид
()
() ( )
()
()
2
2
2
12
2
0
exp
2
exp 1 .
n
n
n
an
Tt t
na a n
cd
⎛⎞
π
⎛⎞
=− ×
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
⎛⎞
⎛⎞
ππ
⎛⎞
×+ τψτ−−ψττ
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
⎝⎠
∫
(3.69)
Чтобы удовлетворить решение начальному условию (3.59), потребуем
выполнение
() () ()
1
,0 0 sin
n
n
n
vx T x x
∞
=
π
=⋅=ϕ
∑
,
откуда
() ()
0
2
0si
nn
n
Tc x x
π
== ϕ ⋅
∫
ndx
. (3.70)
Функция
определена
()
n
Tt
() ()
() ( ) ()
()
2
0
2
2
12
2
0
2
exp sin
2
exp 1 .
n
n
an nx
Tt t x dx
na an
d
⎛⎞
ππ
⎛⎞ ⎛
=
−⋅⋅ϕ +
⎜⎟
⎜⎟ ⎜
⎜⎟
⎝⎠ ⎝
⎝⎠
⎞
⎛⎞
ππ
⎛⎞
+⋅τ⋅ψτ−−ψ
⎟
⎜⎟
⎜⎟
⎜⎟
⎟
⎝⎠
⎝⎠
⎠
∫
∫
ττ
(3.71)
Решение поставленной задачи найдено в виде (3.63), где
определя-
ется по формуле (3.71).
()
n
Tt
Рассмотрим частный случай, когда концы стержня поддерживаются при
постоянных температурах
(
)
1
H
tuψ=,
(
)
2 k
tu
ψ
= .
Тогда (3.71) принимает вид
