Чупров И.Ф., Канева Е.А., Мордвинов А.А. Уравнения математической физики с приложениями к задачам нефтедобычи и трубопроводного транспорта газа
Подождите немного. Документ загружается.

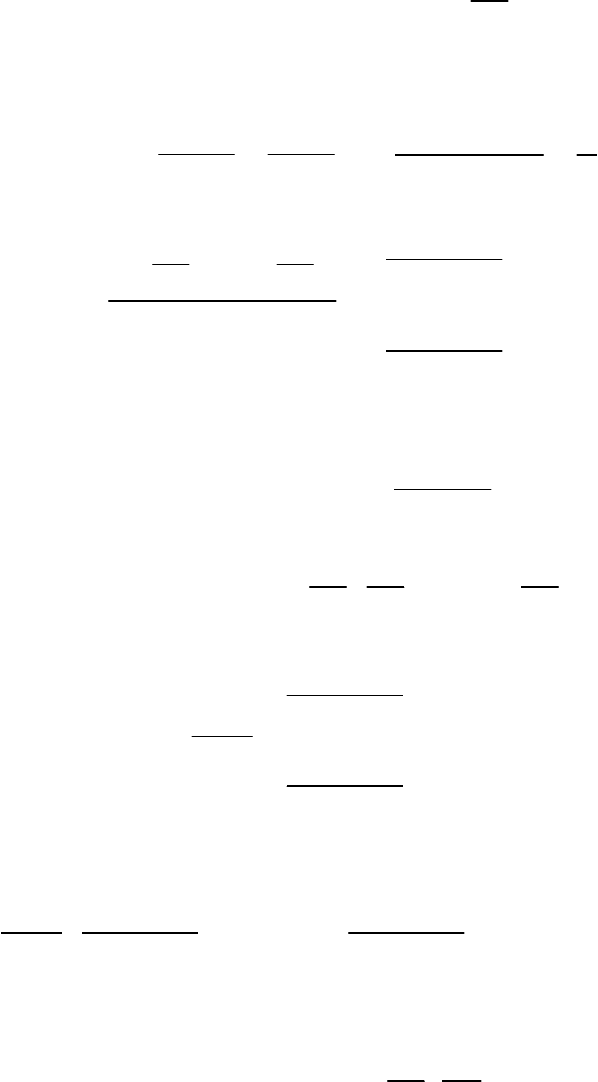
101
Давление в любом сечении определится формулой
() ()
1
,si
n
n
n
n
P
xt P t x
∞
=
π
=⋅
∑
. (4.97)
Учитывая, что
1
sin
2
n
nx x
n
∞
=
π
−
=
∑
;
(
)
1
1sin
2
n
n
nx
x
n
∞
=
−
=
∑
;
(
)
()
1
1
2
1
22
1
1
1
2
при ,
sin sin
при ,
n
xx
nn
xx
xx
n
xx
xx
∞
=
−
⎧
ππ
<
⋅
⎪
⎪
=
⎨
π
−
⎪
>
⎪
⎩
∑
получим
()
()
()
2
2
1
1
1
1
1
,
exp sin
2
при ,
2
при .
Hk
H
n
n
PP
Pxt P
cn n
ct
a
xx
xx
aG
F
xx
xx
∞
=
x
−
=− −
⎛⎞
ππ
⎛⎞
−
⋅− ⋅
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
−⎧
<
⎪
⎪
−⋅
⎨
−
⎪
>
⎪
⎩
∑
−
(4.98)
Последние слагаемые (4.98) можно было бы записать в виде
()
()
(
)
() ( )
()
11
11
2
.
xx xx
aG
xx x xx
F
−−
⎛⎞
σ− − σ −σ−
⎜⎟
⎝⎠
Имея давление, можно найти массовый расход через любое сечение
()
,
2
FP
Mxt
ax
∂
=
−⋅
∂
.
§ 9. Обобщенные функции
Единичная функция Хевисайда.
При решении задач нефтепромысловой
механики широко используются единичная функция Хевисайда и дельта-
функция Дирака. Рассмотрим эти функции, их основные свойства и правила
обращения с ними.
102
()
при 0,
0 при 0
at
t
t
>
⎧
ϕ=
⎨
<
⎩
называется функцией Хевисайда.
Если
, то
1a =
()
1 при 0,
0 при 0
t
t
t
>
⎧
σ=
⎨
<
⎩
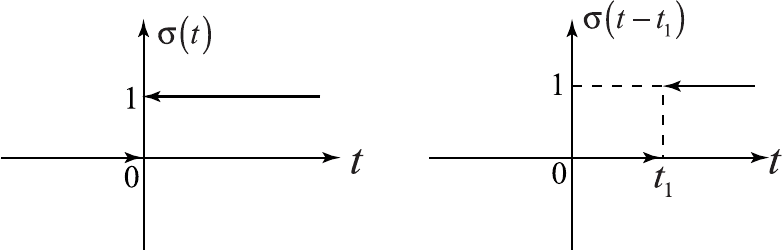
называется единичной функцией Хевисайда. График этой функции изображен
на рис. 4.2.
Рис. 4.2 Рис. 4.3
Используя известные свойства функций, рассмотрим
()
1
1
1
1 при ,
0 при .
tt
tt
tt
>
⎧
σ− =
⎨
<
⎩
График этой функции изображен на рис. 4.3.
В задачах нефтепромысловой механики иногда удобно пользоваться ком-
бинацией единичных функций от различных переменных (например по време-
ни
t
или координате ). Пусть линейный источник мощностью действует на
промежутке времени
[
x
h
]
12
,tt , т.е.
()
1
12
2
0 при ,
при ,
0 при .
tt
thttt
tt
<
⎧
⎪
ϕ= <<
⎨
⎪
>
⎩
Выразим
(
)
tϕ через единичную функцию
()()
1
12 1
2
000при ,
101при ,
11 0при ,
tt
tt tt t tt
tt
2
−
=<
⎧
⎪
σ− −σ− = −= <<
⎨
⎪
−= >
⎩
103
откуда
.
() ( ) ( )
()
12
t h tt ttϕ=σ−−σ−
Если источник действовал при
[
]
12
,ttt
∈
на участке
[
]
12
,xxx
∈
, то
() ( )
(
)
(
)
(
)
(
)
(
)
121
,xt xx xx tt ttϕ=σ−−σ−⋅σ−−σ−
2
.
Из приведенных примеров следует, что с помощью единичной функции
удобно записывать условия того, что какой-либо физический процесс начина-
ется с некоторого момента времени и заканчивается в определенный момент
(цикличность отбора жидкости из скважин, отбор из трубопровода в опреде-
ленный промежуток времени), учитывать несовершенство скважин и т.д.
При интегрировании
функций, содержащих единичную функцию, следу-
ет учесть, что
() ( )
()
()
1
11
1
, если ,
, если ,
0, если .
b
a
bb
aa
fxdx x a
f
xxxdx fxdx ax
xb
⎧
<
⎪
⎪
⎪
⎪
⋅σ − = < <
⎨
⎪
⎪
>
⎪
⎪
⎩
∫
∫∫
b
Дельта-функция. Функция, обладающая свойствами:
1)
равна нулю при всех
0x
≠
;
2)
обращается в бесконечность при
0x
=
;
3)
интеграл от этой функции, взятый в пределах
(
)
,
−
∞+∞ , равен еди-
нице; называется дельта-функцией Дирака и обозначается
. Та-
ким образом,
()
xδ
()
0 при 0,
при 0
x
x
x
≠
⎧
δ=
⎨
∞=
⎩
и
()
1xdx
∞
−∞
δ
=
∫
.
При помощи дельта-функции удобно записывать действие источников или
стоков в отдельные моменты времени или в отдельных точках. Если источник
действует в точке с координатой
, то дельта-функция имеет вид .
Функция
означает действие источника в момент времени .
1
x
()
1
xxδ−
(
1
ttδ−
)
1
t
Выражение
()
(
)
()
(
)
12
xx xx tt
1
σ
−−σ− ⋅δ−
означает, что источник
действовал на отрезке
[
]
12
,xx в момент времени . Аналогично,
1
tt=

104
()()
()
(
12
tt tt xxσ− −σ− ⋅δ −
)
1
означает, что источник действовал в точке
в промежутке времени
[
1
xx=
]
12
,tt .
Следует отметить, что для дельта-функции не существует никакого явно-
го выражения. Поэтому она не может входить ни в какие окончательные соот-
ношения. Отметим также, что дельта-функция является размерной величиной и
имеет размерность, обратную размерности аргумента. Кстати, функция Хеви-
сайда безразмерна.
Приведем некоторые интегральные соотношения, связанные с дельта-
функцией.
1)
() () ()
0,если 0
b
a
x
xdx a b
ϕ
⋅δ =
ϕ
<<
∫
,
2)
() ()
[]
0, если 0,
b
a
x
xdx abϕ⋅δ = ∈
∫
,
3)
()
() ()
00
, если
b
a
0
x
xxdx x ax b
ϕ
⋅δ − =
ϕ
<<
∫
.
Выше рассматривалась дельта-функция одной переменной. В двухмерных
и трехмерных задачах фильтрации, теплового воздействия на пласт и в задачах
трубопроводного транспорта используется дельта-функция на плоскости
и в пространстве
(
,xyδ
) (
)
,,xyzδ .
Для плоскости, например, функция вводится следующим образом:
()
0, если 0 или 0,
,
, если 0
xy
xy
xy
≠
≠
⎧
δ=
⎨
∞==
⎩
и
(
)
,1
Д
f
xydx=
∫
∫
.
Для плоскости и пространства имеют место интегральные соотношения,
аналогичные для одномерного случая.
§ 10. Распространение тепла в пласте
при линейном течении горячей жидкости
При закачке горячей воды в пласт, если пренебречь перетоком тепла в
выше- и нижележащие пласты, температурное поле определяется уравнением
2
2
uu
a
xx
u
t
∂
∂∂
−β =
∂
∂∂
. (4.99)
Наличие конвективного слагаемого связано с движением теплоносителя.
Уравнение (4.99) будем решать при условиях:

105
(
)
0
0
,
t
uxt T
=
=
, (4.100)
(
)
1
0
,
x
uxt T
=
=
, (4.101)
(
)
,
x
uxt
→∞
ограничено.
Применим преобразование Лапласа
() ()()
0
,exp ,uxs stuxtdt
∞
=−
∫
.
Получаем изображающее уравнение
2
0
2
du du
asu
dx dx
T
−
β−=−, (4.102)
где учтено начальное условие.
Для нахождения изображения
u
необходимо решить уравнение (4.102)
при условиях
()
1
0
,
x
T
uxs
s
=
=
, (4.103)
()
,
x
uxs
→∞
ограничено.
Решение уравнения (4.102) при ограниченности
u
, когда имеет
вид
x →∞
()
2
0
,expexp
24
T
s
uxs A x x
s
aa
⎛⎞
ββ
⎛⎞
=+⋅ ⋅ − +
⎜
⎜⎟
⎜
⎝⎠
⎝⎠
a
⎟
⎟
, (4.104)
где
A
определяется из условия (4.103)
0
1
T
T
A
s
s
=+
,
10
TT
A
s
−
=
.
Подставляя
A
в условие (4.104), получаем
()
2
010
,expexp
24
TTT
xx
uxs s
ss a a
a
⎛⎞
−
ββ
⎛⎞
=+ ⋅ ⋅ − +
⎜
⎜⎟
⎜
⎝⎠
⎝⎠
⎟
⎟
. (4.105)
Необходимо перейти к оригиналу по таблицам операционного исчисления.
Решение задачи имеет вид
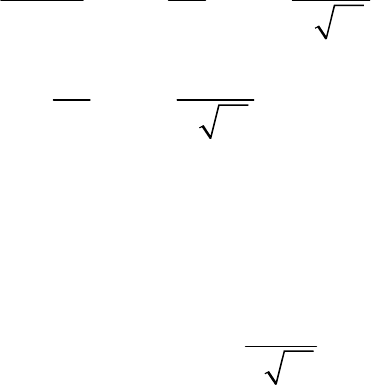
106
()
10
0
,exp
22
2
exp ,
2
2
TT
xx
uxt T erfc
a
at
xxt
erfc
a
at
−
⎛β +β
⎛⎞
=+ ⋅ +
⎜⎟
⎜
⎝⎠
⎝
β−β⎞
⎛⎞
+−⋅
⎜⎟
⎟
⎝⎠
⎠
t
(4.106)
где
1er
f
cz er
f
z=−
; .
()
2
0
exp
z
erfz t dt=−
∫
Если
, то решение при тех же условиях имеет вид
0β=
() ( )
010
,
2
x
uxt T T T erfc
at
=+ − ⋅
.

107
Глава V. Уравнение Лапласа
§ 1. Задачи, приводящие к уравнению Лапласа
Исследования стационарных процессов различной физической природы
(колебания, теплопроводность, диффузия, фильтрация и т.д.) обычно приводят
к уравнениям эллиптического типа. Наиболее распространенным уравнением
этого типа является уравнение Лапласа
0u
∆
=
.
На плоскости
22
22
0
uu
xy
∂∂
+
=
∂∂
.
В пространстве
222
222
0
uuu
xyz
∂∂∂
+
+=
∂∂∂
.
Как было показано в главе III, температура нестационарного температур-
ного поля удовлетворяет уравнению теплопроводности
2
u
au
t
∂
=
∆
∂
.
Если процесс стационарен (не зависит от времени), то
0
u
t
∂
=
∂
, и урав-
нение теплопроводности переходит в уравнение Лапласа.
При наличии внутри рассматриваемого тела источников тепла получим
уравнение
(
)
,,ufxyz∆=− ,
где
()
,,
F
fxyz=
λ
. Здесь – плотность тепловых источников, – коэффи-
циент теплопроводности. Неоднородное уравнение Лапласа принято называть
уравнением Пуассона.
F
λ
Рассмотрим некоторый объем
V
, ограниченный поверхностью . Задача
о стационарном распределении температуры
σ
(
)
,,uxyz внутри тела
V
форму-
лируется следующим образом: найти функцию
(
)
,,uxyz, удовлетворяющую
внутри
V
уравнению
(
)
,,yufxz∆=−
)
z
и граничному условию, которое может
быть взято в одном из следующих видов:
1)
на – первая краевая задача;
(
,,uxy=ϕ
σ
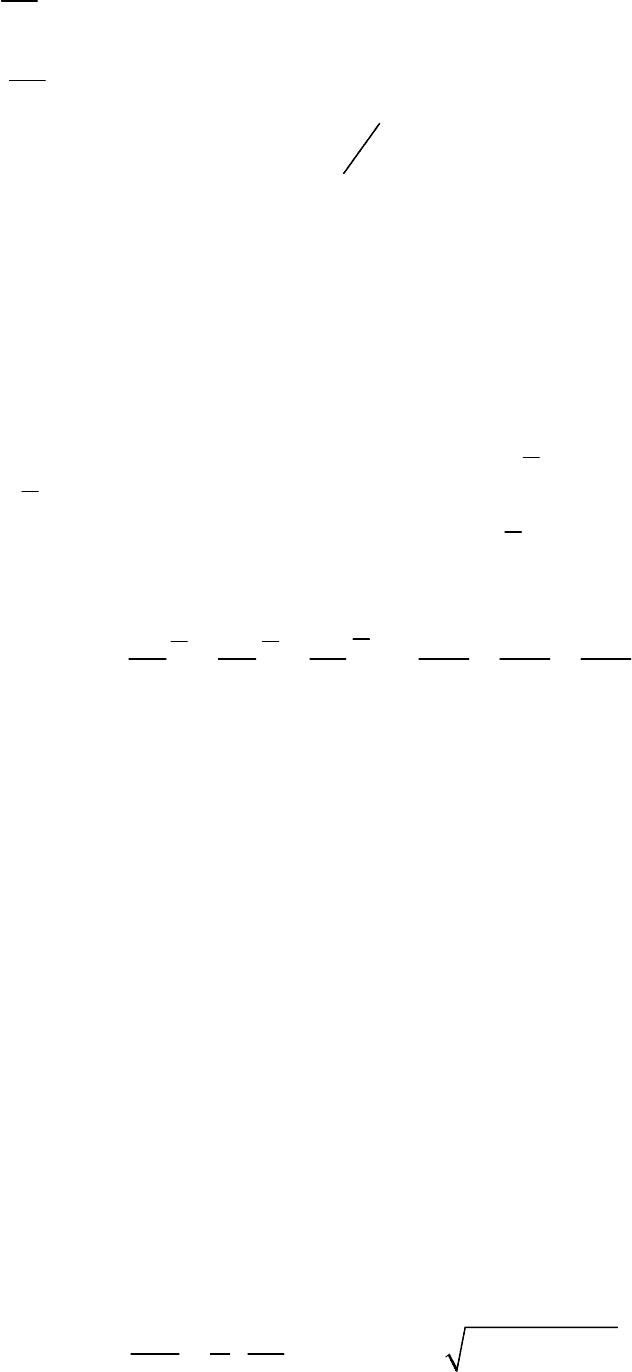
108
2)
(
,,
u
x
)
y
z
n
∂
=Ψ
∂
на – вторая краевая задача;
σ
3)
()
0
u
hu
n
∂
+⋅ −χ=
∂
на
σ
– третья или смешанная краевая задача.
Здесь
– заданные функции,
,,ϕψχ
u
n
∂
∂
– производная по внешней нормали к
поверхности
. Первую краевую задачу часто называют задачей Дирикле, а
вторую – задачей Неймана.
σ
В качестве второго примера рассмотрим потенциальное течение жидко-
сти без источников и стоков. Напомним, что поле
(
)
up называется потенци-
альным, если
.
()
rot 0up=
Пусть внутри некоторого объема
с границей
V
σ
имеет стационарное
течение жидкости (плотность
const
ρ
=
), характеризуемое скоростью
(
)
vp.
Если течение жидкости не вихревое, то скорость
v
является потенциальным
вектором
g
radv =− ϕ
, где – скалярная функция, называемая потенциалом
скорости. Если отсутствуют источники, то
ϕ
div 0v
=
. Подставляя, получим
div
g
rad 0ϕ=
. Перейдем к координатам в пространстве
222
222
0
u
div i j k
xyz xyz
⎛⎞
∂ϕ ∂ϕ ∂ ∂ ϕ ∂ ϕ ∂ ϕ
++ =++=
⎜⎟
∂∂∂ ∂∂∂
⎝⎠
,
т.е. потенциал скорости удовлетворяет уравнению Лапласа.
§ 2. Гармонические функции
Рассмотрим уравнение Лапласа на плоскости или в пространстве
0u
∆
=
. (5.1)
Определение. Функция
(
)
uup
=
, имеющая непрерывные частные произ-
водные второго порядка и удовлетворяющая уравнению Лапласа (5.1) в некото-
рой области D, называется гармонической в этой области.
Простейшими примерами гармонических функций являются линейные
функции:
uaxb
y
c=++
на плоскости и
uaxb
y
cz d
=
+++
в пространстве.
Особый интерес представляют решения уравнений Лапласа, обладающие сфе-
рической или цилиндрической (в случае двух независимых переменных – кру-
говой) симметрией.
Решение
, обладающее сферической симметрией, будет опреде-
ляться из обыкновенного дифференциального уравнения
()
uur=
2
2
2
0
uu
rrr
∂∂
+⋅ =
∂
∂
, где
22
rxyz
2
=
++.
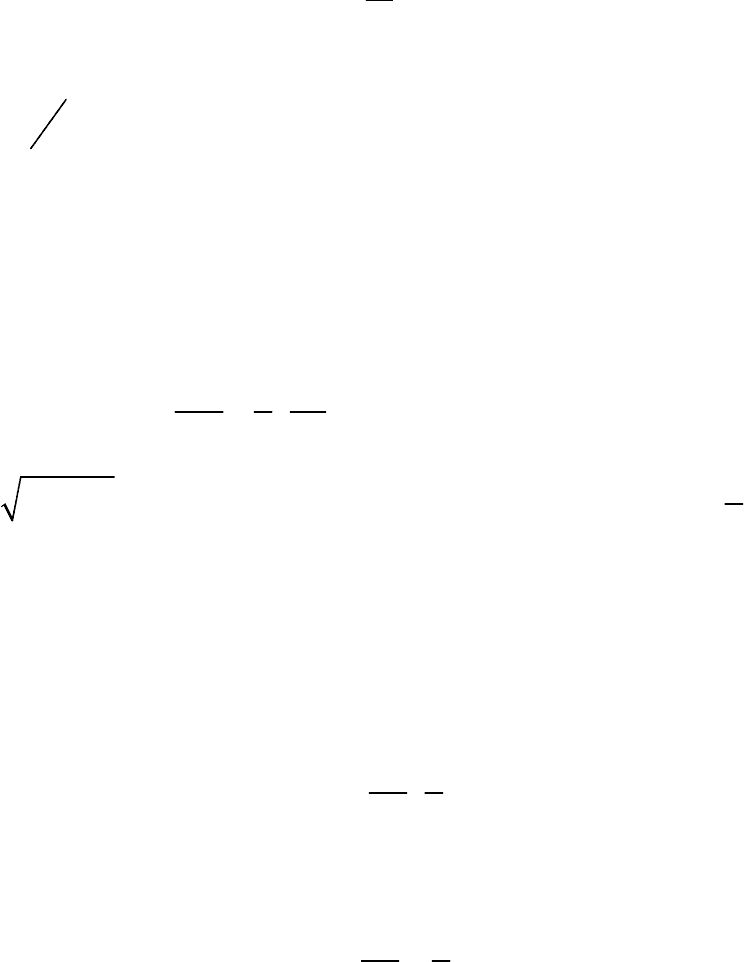
109
Это уравнение получится, если подставить искомую функцию в уравне-
ние Лапласа (5.1), записанное в сферических координатах (см. главу II). Интег-
рируя это уравнение, находим
1
2
c
uc
r
=
+
,
где и – произвольные постоянные. Полагая
1
c
2
c
1
1c
=
,
2
0c
=
, получим функ-
цию
0
1
u
r
=
, которую часто называют фундаментальным решением уравне-
ния Лапласа в пространстве. Функция
является гармонической всюду в
пространстве, кроме начала координат.
0
u
Аналогично, полагая
(
)
uur= и пользуясь уравнением Лапласа в цилин-
дрических или полярных координатах (см. главу II), найдем решения, обла-
дающие цилиндрической или круговой симметрией
2
12
2
1
0ln
uu
uc rc
rrr
∂∂
+⋅ =⇒= +
∂∂
,
где
2
rxy=+
2
. Выбирая
1
1c
=
−
и
2
0c
=
, будем иметь
0
1
lnu
r
=
, которую
называют фундаментальным решением уравнения Лапласа на плоскости.
Фундаментальные решения уравнения Лапласа имеют помимо большого
значения в теории гармонических функций важный физический смысл.
Рассмотрим в пространстве электрическое поле, образованное точечным
зарядом величины
q, помещенным в начало координат. Тогда потенциал этого
поля равен
1
4
q
u
r
=
⋅
π
.
Если рассмотреть поле, создаваемое заряженной прямой, то потенциал
такого поля будет равен
1
1
ln
2
q
u
r
=
π
,
где – линейная плотность заряда (величине заряда, рассчитанной на единицу
длины).
1
q
§ 3. Свойства гармонических функций
Теорема о среднем. Пусть функция
(
)
,uuxy
=
гармоническая в некото-
ром круге
D радиуса R c центром
(
)
00
,xy и непрерывная в соответствующем
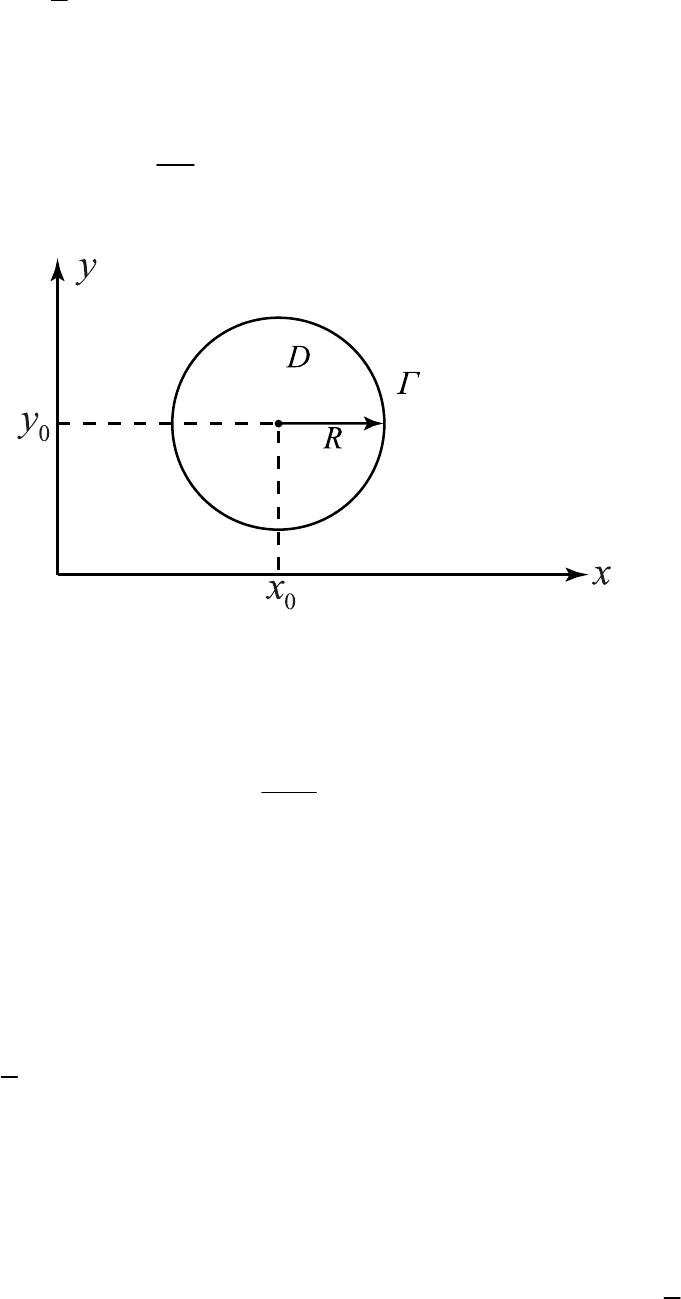
110
замкнутом круге
DDГ
=
∪
. Тогда значение этой функции в центре круга рав-
но ее среднему значению на окружности
Г, ограничивающей данный круг
(рис. 5.1), т.е.
() (
2
00 0 0
0
1
,cos,
2
ux y ux R y R d
π
=+ϕ+ϕ
π
∫
)
sin
ϕ. (5.2)
Рис. 5.1
Формуле (5.2) можно придать другой вид
() ()
00
2
1
,,
D
u x y u x y dxdy
R
=
π
∫∫
. (5.3)
Имеет место и обратная теорема: если в некоторой области
D функция
(
)
,uuxy= непрерывная и для каждой точки
(
)
00
,xy D
∈
выполняется теоре-
ма о среднем в любом сколь угодно малом круге с центром в точке
(
)
00
,xy, то
эта функция гармоничная в
D.
Принцип максимума. Если функция
(
)
,uxy непрерывна в области D и на
ее границе
(
DDГ= ∪
)
)
, удовлетворяет уравнению Лапласа (гармонична) в
области
D, то максимальные и минимальные значения функции дости-
гаются на границе
Г, т.е.
(
,uxy
()
()
(
)
()
(
)
,
,
min , , max ,
xy Г
xy Г
ux
y
ux
y
ux
y
∈
∈
≤
≤
. (5.4)
Следствие. Если функция
(
)
,uuxy
=
непрерывна в области D и гармо-
нична в области
D, то
