Чулков П.В. Уравнения и неравенства в школьном курсе математики
Подождите немного. Документ загружается.

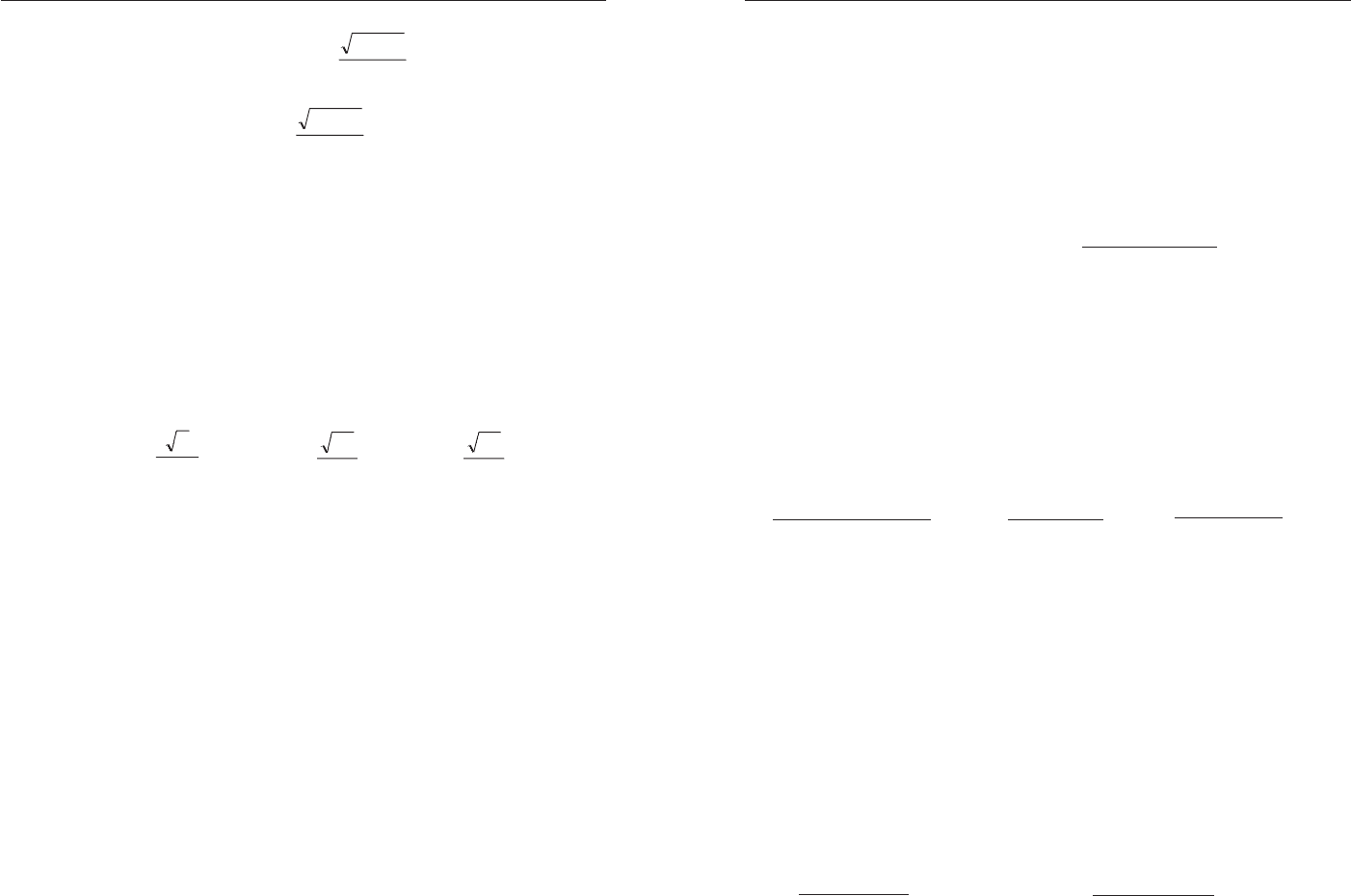
40
41
Ìåòîäû ðåøåíèÿ íåðàâåíñòâ
Ëåêöèÿ 2
Òåîðåìà 13. Åñëè ôóíêöèÿ
)
(
xp
óáûâàåò íà íåêîòîðîì ïðîìå-
æóòêå, òî íåðàâåíñòâà
0
)
(
)
(
>−
bpap
è
0<−
ba
ðàâíîñèëüíû íà
ÎÄÇ.
 âèäå ñõåìû:
() ()
00,
() ()
00,
() ()
00.
pa pb a b
pa pb a b
pa pb a b
−>⇔−<
−<⇔−>
−=⇔−=
Ïðèìåð 17. Ðåøèòå íåðàâåíñòâî
0
6
)
23
(
2211
>
−
−−
x
xx
.
Ðåøåíèå. Äàííîå íåðàâåíñòâî èìååò âèä
0
)
(
)
(
>⋅
xgxf
, ãäå
11211
)
(
)
23
(
)
(
xxxf
−−=
.
Ïóñòü
11
)
(
xxp
=
,
)
(
xp
âîçðàñòàåò íà ìíîæåñòâå âñåõ äåé-
ñòâèòåëüíûõ ÷èñåë. Òîãäà ïðîìåæóòêè çíàêîïîñòîÿíñòâà
)
(
xf
ñî-
âïàäàþò ñ ïðîìåæóòêàìè çíàêîïîñòîÿíñòâà
2
1
)
23
(
)
(
xxxf
−−=
, è
íåðàâåíñòâî
0
)
(
)
(
>⋅
xgxf
ðàâíîñèëüíî íåðàâåíñòâó
0
)
(
)
(
1
>⋅
xgxf
.
Ñëåäîâàòåëüíî,
0
)
(
)
23
(
2
>−−
xpxp
⇔
0
)
23
(
2
>−−
xx
, è
0
6
)
(
)
23
(
11211
>
−
−−
x
xx
⇔
0
6
23
2
>
−
−−
x
xx
⇔
0
6
)
2
)(
1
(
<
−
−−
x
xx
.
Äàëåå, âîñïîëüçîâàâøèñü ìåòîäîì èíòåðâàëîâ äëÿ ðàöèîíàëü-
íûõ ôóíêöèé, ïîëó÷èì îòâåò:
(
;1
)(
2; 6
)
−∞ ∪
.
Ïðîâåðüòå ýòî ñàìîñòîÿòåëüíî.
 äàëüíåéøåì ìû íå ðàç óáåäèìñÿ, ÷òî ïðèìåíåíèå ìåòîäà çà-
ìåíû ìíîæèòåëåé äëÿ ñâåäåíèÿ ðåøåíèÿ íåðàâåíñòâà ê ìåòîäó
èíòåðâàëîâ ñóùåñòâåííî ñíèæàåò îáúåì ðåøåíèÿ.
Óïðàæíåíèÿ äëÿ ñàìîñòîÿòåëüíîé ðàáîòû
Ðåøèòå êâàäðàòè÷íûå íåðàâåíñòâà (14).
1.
0243
2
≤+−
xx
. 2.
096
2
≤+−
xx
.
3.
017
2
>+−
xx
. 4.
023
2
>+−
xx
.
Ðåøèòå íåðàâåíñòâà ìåòîäîì èíòåðâàëîâ (59).
5.
0
)
2
)(
3
(
)
4
)(
1
(
>
−+
−+
xx
xx
.6.
0
5
)
2
)(
2
(
2
≤
+
−+
x
xx
.
Ïðèìåð 16. Ðåøèòå íåðàâåíñòâî
0
2
11
2
≥
+
+
xx
x
.
Ðàññìîòðèì ôóíêöèþ
xx
x
xf
2
11
)
(
2
+
+
=
.
1) Îáëàñòü îïðåäåëåíèÿ ôóíêöèè
)
(
xf
íàõîäèì èç ñèñòåìû íå-
ðàâåíñòâ
11−≥x ,
02
2
≠+
xx
.
Îáëàñòü îïðåäåëåíèÿ:
[
11, 2
)(
2; 0
)(
0;
)
−−∪− ∪+∞.
2) Óðàâíåíèå
0
)
(
=
xf
èìååò åäèíñòâåííûé êîðåíü: 11.
Òàêèì îáðàçîì, îáëàñòü îïðåäåëåíèÿ ôóíêöèè
)
(
xf
ñîñòîèò èç
ñëåäóþùèõ èíòåðâàëîâ çíàêîïîñòîÿíñòâà (11, 2), (2; 0),
(
0;
)
+∞
.
3) Îïðåäåëèì çíàê ôóíêöèè
)(xf
íà êàæäîì èç èíòåðâàëîâ
çíàêîïîñòîÿíñòâà. Ïîëó÷èì:
0
69
8
)
3
(
>
−
=−
f
,
0
21
10
)
1
(
<
−
=−
f
,
0
21
12
)
1
(
>
+
=
f
.
Íåðàâåíñòâî íåñòðîãîå, ïîýòîìó 11 âõîäèò â ìíîæåñòâî ðåøåíèé.
Îòâåò:
[
11;2
)(
0;
)
−∪+∞.
Ìåòîä çàìåíû ìíîæèòåëåé
Åñëè îáëàñòè îïðåäåëåíèÿ, íóëè è ïðîìåæóòêè çíàêîïîñòîÿí-
ñòâà ôóíêöèé
)
(
xf
è
)
(
1
xf
ñîâïàäàþò, òî èíîãäà áûâàåò âûãîäíî
âìåñòî íåðàâåíñòâà
0
)
(
)
(
∨⋅
xgxf
ðåøàòü íåðàâåíñòâî
0
)
(
)
(
1
∨⋅
xgxf
.
 ÷àñòíîñòè, ìîæíî ðàçíîñòü çíà÷åíèé ìîíîòîííûõ ôóíêöèé
çàìåíèòü ðàçíîñòüþ çíà÷åíèé èõ àðãóìåíòîâ.
Òåîðåìà 12. Åñëè ôóíêöèÿ
)
(
xp
âîçðàñòàåò íà íåêîòîðîì ïðî-
ìåæóòêå, òî íåðàâåíñòâà
0
)
(
)
(
>−
bpap
è
0>−
ba
ðàâíîñèëüíû
íà ÎÄÇ.
Èëè â âèäå ñõåìû:
() ()
00;
() ()
00;
() ()
00.
pa pb a b
pa pb a b
pa pb a b
−>⇔−>
−<⇔−<
−=⇔−=
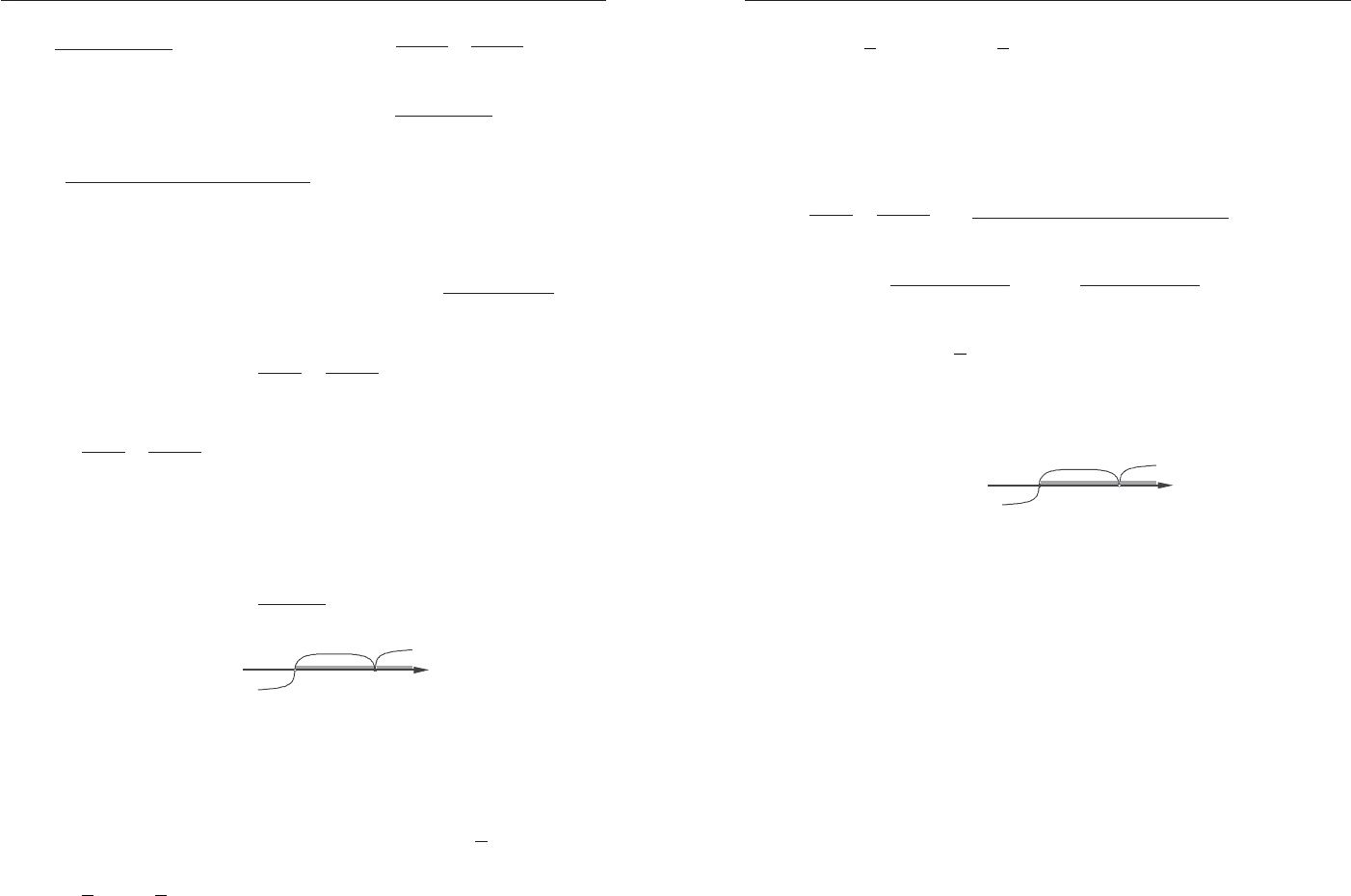
42
43
Ìåòîäû ðåøåíèÿ íåðàâåíñòâ
Ëåêöèÿ 2
11.
) )
17
;1;22;3;
23
−∞ − ∪ ∪ ∪ +∞
. 12.
()
;1 1;
−∞ − ∪ +∞
.
13. [3; 4]. 14.  õîäå ïðåîáðàçîâàíèé îáå ÷àñòè íåðàâåíñòâà
óìíîæèëè íà îáùèé çíàìåíàòåëü. Ïðè ýòîì íå áûëî ó÷òåíî, ÷òî
âûðàæåíèå
)14)(2( −+ xx
ìîæåò ïðèíèìàòü êàê ïîëîæèòåëüíûå,
òàê è îòðèöàòåëüíûå çíà÷åíèÿ. Ïðàâèëüíîå ðåøåíèå:
14
32
2
2
−
−
≥
+
−
x
x
x
x
⇔
0
)
14
)(
2
(
)
2
)(
32
(
)
14
)(
2
(
≥
−+
+−−−−
xx
xxxx
⇔
⇔
0
)
14
)(
2
(
45
2
≥
−+
+−
xx
xx
⇔
0
)
14
)(
2
(
)
4
)(
1
(
≥
−+
−−
xx
xx
.
Îòâåò:
()
1
;2 ;1 [4; )
4
−∞ − ∪ ∪ +∞
.
15. Íåðàâåíñòâî ñòðîãîå, ïîýòîìó ÷èñëî
5
, ïðè êîòîðîì ëåâàÿ
÷àñòü íåðàâåíñòâà îáðàùàåòñÿ â 0, íå ÿâëÿåòñÿ åãî ðåøåíèåì.
Ïðàâèëüíûé ðèñóíîê (ðèñ. 11):
N
+
−
+
#
Ðèñ. 11
Îòâåò:
(
1; 5
)(
5;
)
∪+∞
.
7.
1
)
1
)(
13
(
1314
≥
+−
−
xx
x
. 8.
12
2
13
2
−
−
≤
+
+
x
x
x
x
.
9.
0
)
2811
)(
86
(
22
<+−+−
xxxx
. 10.
x
xx
xx
≤
++
++
34
43
2
2
.
11.
()
()
()()
0
)
243
(
273
1352
2
2
2
≥
+−−−
−−−
xxxx
xxx
.
Ïðè ðåøåíèè íåðàâåíñòâà âîñïîëüçóéòåñü ìåòîäîì çàìåíû ïå-
ðåìåííûõ (1213).
12.
032
24
≥−+
xx
. 13.
.0
177
20
167
2
2
≤
+−
−+−
xx
xx
Óêàæèòå è èñïðàâüòå îøèáêè â ðåøåíèè íåðàâåíñòâà (1415).
14. Ðåøèòå íåðàâåíñòâî
14
32
2
2
−
−
≥
+
−
x
x
x
x
.
Ðåøåíèå.
14
32
2
2
−
−
≥
+
−
x
x
x
x
⇔
)
2
)(
32
(
)
14
)(
2
(
+−≥−−
xxxx
⇔
⇔
08102
2
≥+−
xx
⇔
⇔
045
2
≥+−
xx
⇔
0
)
4
)(
1
(
≥−−
xx
.
Îòâåò:
(
;1
][
4;
)
−∞ ∪ +∞
.
15. Ðåøèòå íåðàâåíñòâî
0
1
)
5
(
2
>
−
−
x
x
.
Ðåøåíèå. Âîñïîëüçóåìñÿ ìåòîäîì èíòåðâàëîâ (ðèñ. 10), ïîëó÷èì:
N
+
−
+
#
Ðèñ. 10
Îòâåò:
);1( +∞
.
Îòâåòû, óêàçàíèÿ, ðåøåíèÿ
1. Íåò ðåøåíèé. 2.
3
. 3.
)
;
(
∞−∞
. 4.
(
;1
)(
2;
)
−∞ ∪ ∞
.
5.
(
;3
)(
1; 2
)(
4;
)
−∞ − ∪ − ∪ +∞
. 6.
{}
(
5; 2
]
2
−−∪
. 7.
{}
2
)
3
1
;1
(
∪−
.
8.
()
11
;0;8;
32
−∞ − ∪ ∪ +∞
. 9.
(
2; 4
)(
4;7
)
∪
. 10.
() )
3; 1 1;
∪+∞
.

44
45
Ìåòîäû ðåøåíèÿ ñèñòåì óðàâíåíèé
Ëåêöèÿ 3
Èëè, â âèäå ñõåìû:
Åñëè
)
,,
(
)
,
(
)
,
(
)
,
(
2211
yxgyxfyxgyxf
=⇔=
òî
=
=
)
,
(
)
,
(
)
,,
(
)
,
(
11
yxgyxf
yxgyxf
⇔
=
=
)
,
(
)
,
(
)
,,
(
)
,
(
22
yxgyxf
yxgyxf
.
Ïðèìåð 1. Åñëè â ñèñòåìå óðàâíåíèé
22
6,
22
xy
xxy
+=
−=
óðàâíåíèå
6=+
yx
çàìåíèòü íà óðàâíåíèå
yx
−= 6
, òî ïîëó÷èì ðàâíîñèëü-
íóþ ñèñòåìó
=−
−=
.22
,6
22
yxx
yx
Òåîðåìà 2. Åñëè îäíî èç óðàâíåíèé ñèñòåìû çàìåíèòü íà ñóì-
ìó óðàâíåíèé ñèñòåìû, òî ïîëó÷åííàÿ ñèñòåìà óðàâíåíèé áóäåò
ðàâíîñèëüíà èñõîäíîé.
 âèäå ñõåìû:
11
11
11
(,) (, ) (,) (,),
(,) (,),
(,) (,)
(,) (,).
fxy f xy gxy g xy
fxy gxy
fxy g xy
fxy g xy
+=+
=
⇔
=
=
Ïðèìåð 2. Åñëè â ñèñòåìå óðàâíåíèé
2
34,
0
xy
xy
+=
−=
óðàâíåíèå
0
2
=−
yx
çàìåíèòü íà óðàâíåíèå
43
2
=+
xx
, òî ïîëó÷èì ðàâíî-
ñèëüíóþ ñèñòåìó
=+
=+
.43
,43
2
xx
yx
Òåîðåìà 3. Åñëè â îäíîì èç óðàâíåíèé ñèñòåìû âûðàçèòü îäíó
èç ïåðåìåííûõ ÷åðåç äðóãóþ, ïîäñòàâèòü ïîëó÷åííîå âûðàæåíèå
âî âòîðîå óðàâíåíèå, òî ïîëó÷åííàÿ ñèñòåìà áóäåò ðàâíîñèëüíà
èñõîäíîé ñèñòåìå.
 âèäå ñõåìû:
Åñëè
)
,
(
)
,
(
)
,
(
11
ypxyxgyxf
=⇔=
òî
=
=
)
,
(
)
,
(
)
,,
(
)
,
(
11
yxgyxf
yxgyxf
⇔
11
(),
((),) ((),).
xpy
fpyy gpyy
=
=
Ïîñëåäíåå ïðåîáðàçîâàíèå ñëóæèò îñíîâîé òàê íàçûâàåìîãî
ìåòîäà ïîäñòàíîâêè (èëè èíà÷å: ìåòîä ïîñëåäîâàòåëüíîãî èñêëþ-
Ëåêöèÿ 3
Ìåòîäû ðåøåíèÿ ñèñòåì óðàâíåíèé
Çàäà÷à î ðåøåíèè ñèñòåì óðàâíåíèé ñ íåñêîëüêèìè ïåðåìåí-
íûìè òðóäíà, è â îáùåì ñëó÷àå åå íåëüçÿ ðåøèòü ñðåäñòâàìè ýëå-
ìåíòàðíîé àëãåáðû.
Îäíàêî èíîãäà, êîìáèíèðóÿ íåêîòîðûå èçâåñòíûå ìåòîäû ðå-
øåíèÿ: ïîäñòàíîâêè è àëãåáðàè÷åñêîãî ñëîæåíèÿ, çàìåíû ïå-
ðåìåííûõ, óäàåòñÿ íàéòè ïóòü ê ðåøåíèþ ñèñòåìû. Ïðè ýòîì â
êàæäîì îòäåëüíîì ñëó÷àå ïðèõîäèòñÿ èñïîëüçîâàòü ÷àñòíûå îñî-
áåííîñòè çàäà÷è äëÿ òîãî, ÷òîáû íàéòè óäà÷íûé ìåòîä ðåøå-
íèÿ.
Âíà÷àëå ìû ðàññìîòðèì íåêîòîðûå âîïðîñû òåîðèè ñèñòåì óðàâ-
íåíèé. Äëÿ ïðîñòîòû îãðàíè÷èìñÿ ñèñòåìàìè óðàâíåíèé ñ äâóìÿ
íåèçâåñòíûìè.
Ñèñòåìû àëãåáðàè÷åñêèõ óðàâíåíèé
Íàïîìíèì îñíîâíûå îïðåäåëåíèÿ.
Ïóñòü äàíû äâà óðàâíåíèÿ ñ äâóìÿ ïåðåìåííûìè:
)
,
(
)
,
(
yxgyxf
=
è
)
,
(
)
,
(
11
yxgyxf
=
.
(3.1.) Ðåøåíèåì ñèñòåìû óðàâíåíèé íàçûâàþò óïîðÿäî÷åííóþ
ïàðó ÷èñåë
)
,
(
00
yx
, ïðè êîòîðîé îáà óðàâíåíèÿ ñèñòåìû îáðàùà-
þòñÿ â âåðíûå ðàâåíñòâà.
(3.2.) Ðåøèòü ñèñòåìó óðàâíåíèé îçíà÷àåò íàéòè âñå ðåøå-
íèÿ èëè äîêàçàòü, ÷òî ðåøåíèé íåò.
(3.3.) Äâå ñèñòåìû óðàâíåíèé íàçûâàþò ðàâíîñèëüíûìè, åñëè
ìíîæåñòâà èõ ðåøåíèé ñîâïàäàþò. Ïðèíÿòî ñ÷èòàòü, ÷òî ñèñòåìû
óðàâíåíèé, íå èìåþùèå ðåøåíèé, ðàâíîñèëüíû.
(3.4.) Ñèñòåìà óðàâíåíèé ÿâëÿåòñÿ ñëåäñòâèåì íåêîòîðîé äðó-
ãîé ñèñòåìû, åñëè êàæäîå ðåøåíèå äðóãîé ñèñòåìû ÿâëÿåòñÿ ðå-
øåíèåì äàííîé ñèñòåìû.
Ïðè ðåøåíèè ñèñòåì óðàâíåíèé èõ çàìåíÿþò áîëåå ïðîñòû-
ìè, íî ðàâíîñèëüíûìè ñèñòåìàìè. Ïðè ýòîì ÷àùå âñåãî âûïîë-
íÿþò ïðåîáðàçîâàíèÿ, îñíîâàííûå íà ñëåäóþùèõ óòâåðæäåíè-
ÿõ.
Òåîðåìà 1. Åñëè îäíî èç óðàâíåíèé ñèñòåìû çàìåíèòü íà ðàâ-
íîñèëüíîå óðàâíåíèå, à âòîðîå óðàâíåíèå îñòàâèòü íåèçìåííûì,
òî ïîëó÷èì ñèñòåìó, ðàâíîñèëüíóþ èñõîäíîé.
46
47
Ìåòîäû ðåøåíèÿ ñèñòåì óðàâíåíèé
Ëåêöèÿ 3
Òåîðåìà 4. Åñëè óðàâíåíèå
)
,
(
)
,
(
yxsyxp
=
ÿâëÿåòñÿ ñëåäñòâè-
åì íåêîòîðîé ñèñòåìû óðàâíåíèé, òî ñèñòåìà, ïîëó÷åííàÿ ïðèñî-
åäèíåíèåì óðàâíåíèÿ
)
,
(
)
,
(
yxsyxp
=
ê èñõîäíîé ñèñòåìå, åé ðàâ-
íîñèëüíà.
 âèäå ñõåìû:
Åñëè
11
(,) (,),
(;) (;)
(,) (, )
fxy gxy
pxy sxy
fxy g xy
=
⇒=
=
, òî
=
=
)
,
(
)
,
(
)
,,
(
)
,
(
11
yxgyxf
yxgyxf
⇔
=
=
=
)
.,
(
)
,
(
)
,,
(
)
,
(
)
,,
(
)
,
(
11
yxsyxp
yxgyxf
yxgyxf
Ïðèìåð 5. Ðåøèòå ñèñòåìó óðàâíåíèé
=−−+
=−−+
.0320310
,0733
222
222
xyxyx
xyxyx
Ðåøåíèå. Åñëè ïåðâîå óðàâíåíèå ñèñòåìû óìíîæèòü íà 3,
à çàòåì ñëîæèòü ñî âòîðûì, òî ïîëó÷èì óðàâíåíèå
01811
22
=+−
xyyx
, êîòîðîå ÿâëÿåòñÿ ñëåäñòâèåì èñõîäíîé ñèñ-
òåìû (ïîäóìàéòå ïî÷åìó).
Òàêèì îáðàçîì,
22 2
22 2
3370,
10 3 20 3 0
xy x xy
xy x xy
+− −=
+− −=
⇔
22 2
22 2
22
3370,
10 3 20 3 0,
11 18 0.
xy x xy
xy x xy
xy xy
+− −=
+− −=
−+=
Ðåøàåì óðàâíåíèå
01811
22
=+−
xyyx
ñ ïîìîùüþ ïîäñòàíîâ-
êè
axy
=
, ïîëó÷èì:
2
11 18 0
aa
−+=
, îòêóäà
9
1
=
a
è
2
2
=
a
.
Èñõîäíàÿ ñèñòåìà ðàâíîñèëüíà ñîâîêóïíîñòè ñèñòåì
22 2
22 2
3370,
10 3 20 3 0,
2
xy x xy
xy x xy
xy
+− −=
+− −=
=
è
=
=−−+
=−−+
.9
,0320310
,0733
222
222
xy
xyxyx
xyxyx
÷åíèÿ íåèçâåñòíûõ), êîòîðûé ñâîäèò ðåøåíèå ñèñòåìû óðàâíåíèé
ê ðåøåíèþ óðàâíåíèÿ ñ îäíîé ïåðåìåííîé.
Ïðèìåð 3. Ðåøèòå ñèñòåìó óðàâíåíèé
=+
=−−
xyyy
yx
32
2
,01
.
Ðåøåíèå. Ïðèìåíèì ìåòîä ïîäñòàíîâêè. Ïðåîáðàçóåì èñõîä-
íóþ ñèñòåìó:
=+
+=
xyyy
yx
32
2
,1
⇔
+=+
+=
yyyy
yx
)
1
(
,1
232
2
⇔
=−
+=
0
,1
2
2
yy
yx
⇔
⇔
2
1,
0
1
xy
y
y
=+
=
=
⇔
0,
1
1,
2.
y
x
y
x
=
=
=
=
Îòâåò: (1; 0), (2; 1).
Ïðèìåð 4. Ðåøèòå ñèñòåìó óðàâíåíèé
=−
−=+−−
.1
,233
22
2233
yxx
xyxyx
Ðåøåíèå. Óìíîæèì âòîðîå óðàâíåíèå íà 3.
Ïîëó÷åííîå óðàâíåíèå ñëîæèì ñ ïåðâûì óðàâíåíèåì:
=−
=+−−
.1
,133
22
2233
yxx
xyyxyx
⇔
=−
=−
.1
,1
)
(
22
3
yxx
yx
⇔
=−
=−
.1
,1
22
yxx
yx
⇔
⇔
=−
−=
.1
,1
22
yxx
xy
Âûïîëíèì ïîäñòàíîâêó y = x 1 âî âòîðîì óðàâíåíèè.
Ïîëó÷èì:
012
23
=+−
xx
.
Êîðíè óðàâíåíèÿ:
1
1
=
x
,
2
51
2
+
=
x
,
2
51
3
−
=
x
.
Îòâåò: (1; 0),
+−+
2
51
;
2
51
,
−−−
2
51
;
2
51
.

48
49
Ìåòîäû ðåøåíèÿ ñèñòåì óðàâíåíèé
Ëåêöèÿ 3
Çàìåíà ïåðåìåííûõ
Ïðè ðåøåíèè ñèñòåì óðàâíåíèé ÷àñòî èñïîëüçóåòñÿ ìåòîä ââå-
äåíèÿ íîâûõ ïåðåìåííûõ (ìåòîä çàìåíû).
Ñóòü ìåòîäà ñîñòîèò â ñëåäóþùåì:
Ïîñêîëüêó:
=
=
=
=
byxs
ayxp
yxsyxpgyxsyxpf
yxsyxpgyxsyxpf
)
,
(
,
)
,
(
))
,,
(
)
,,
(
(
))
,
(
)
,,
(
(
))
,,
(
)
,,
(
(
))
,
(
)
,,
(
(
11
⇔
11
(,) (,),
(,) (,),
(,) ,
(,) ,
fab gab
fab gab
pxy a
sxy b
=
=
=
=
òî ìîæíî âìåñòî ñèñòåìû
11
( ( , ), ( , )) ( ( , ), ( , )),
((, ),(,)) ((,),(,))
fpxy sxy gpxy sxy
f pxy sxy g pxy sxy
=
=
ðåøèòü áîëåå ïðîñòóþ ñèñòåìó
11
(,) (,),
(,) (,).
fab gab
fab gab
=
=
(*)
À çàòåì ñîâîêóïíîñòü ñèñòåì
=
=
,
)
,
(
,
)
,
(
1
1
byxs
ayxp
=
=
,
)
,
(
,
)
,
(
2
2
byxs
ayxp
…
=
=
,
)
,
(
,
)
,
(
n
n
byxs
ayxp
ãäå
)
;
(
11
ba
,
)
;
(
22
ba
, …,
)
;
(
nn
ba
ðåøåíèÿ ñèñòåìû (*).
Èíîãäà ñ ïîìîùüþ çàìåíû ïåðåìåííûõ óäàåòñÿ óïðîñòèòü îäíî
èç óðàâíåíèé ñèñòåìû.
Ïðèìåð 7. Ðåøèòå ñèñòåìó óðàâíåíèé
=−
=
+
−
+
−
+
.12
,
3
10
22
yx
yx
yx
yx
yx
Ðåøåíèå. Ïóñòü
a
yx
yx
=
−
+
, òîãäà ïåðâîå óðàâíåíèå ñèñòåìû
ïðèìåò âèä
3
1
3
1
=+
a
a
, îòêóäà ëåãêî ïîëó÷èòü, ÷òî
3
1
=
a
,
3
1
2
=
a
.
Ñëåäîâàòåëüíî, ïåðâîå óðàâíåíèå ñèñòåìû ðàâíîñèëüíî ñîâîêóï-
íîñòè óðàâíåíèé
3=
−
+
yx
yx
è
3
1
=
−
+
yx
yx
, à èñõîäíàÿ ñèñòåìà ðàâ-
íîñèëüíà ñîâîêóïíîñòè ñèñòåì
Ðåøèì ïåðâóþ ñèñòåìó. Òàê êàê
2=
xy
, òî ïåðâîå óðàâíåíèå
ñèñòåìû ìîæíî ïåðåïèñàòü â âèäå:
,07612
2
=−−+
x
îòêóäà
=
=
2
,1
1
1
y
x
è
2
2
1,
2.
x
y
=−
=−
Ïðîâåðêà ïîêàçûâàåò, ÷òî îáà ðåøåíèÿ óäîâëåòâîðÿþò èñõîä-
íîìó óðàâíåíèþ.
Âòîðàÿ ñèñòåìà ðåøåíèé íå èìååò.
Îòâåò: (1; 2), (1; 2).
Íåêîòîðûå ïðåîáðàçîâàíèÿ ñîõðàíÿþò ðàâíîñèëüíîñòü ñèñòåì
ïðè îïðåäåëåííûõ îãðàíè÷åíèÿõ.
Òåîðåìà 5. Åñëè â ñèñòåìå óðàâíåíèé ñ äâóìÿ ïåðåìåííûìè
îäíî èç óðàâíåíèé ïðåäñòàâëåíî â âèäå ïðîèçâåäåíèÿ, ðàâíîãî
íóëþ, òî ñèñòåìà ðàâíîñèëüíà ñîâîêóïíîñòè äâóõ ñèñòåì íà èõ
îáùåé îáëàñòè äîïóñòèìûõ çíà÷åíèé.
Åñëè x, y ∈ ÎÄÇ èñõîäíîé ñèñòåìû, òî
(
,
)(
,
)
0,
(
,
)(
,
)
fxy gxy
pxy sxy
⋅=
=
⇔
(
,
)
0,
(
,
)(
,
)
(
,
)
0,
(
,
)(
,
)
.
fxy
pxy sxy
gxy
pxy sxy
=
=
=
=
Ïðèìåð 6. Ðåøèòå ñèñòåìó óðàâíåíèé
=+
=−
.6
,04
2
22
xxy
yx
Ðåøåíèå. Ïðåîáðàçóåì èñõîäíóþ ñèñòåìó:
=+
=−
6
,04
2
22
xxy
yx
⇔
=+
=+−
6
,0
)
2
)(
2
(
2
xxy
yxyx
⇔
⇔
2
2
20,
6
20,
6
xy
xy x
xy
xy x
+=
+=
−=
+=
⇔
2
2
2,
26
2,
66.
xy
y
xy
y
=−
=
=
=
Îòâåò: (2; 1), (2; 1),
)
3;32
(
−
,
(
23; 3
)
−
.

50
51
Ìåòîäû ðåøåíèÿ ñèñòåì óðàâíåíèé
Ëåêöèÿ 3
ïåðâîå óðàâíåíèå. Ðåøèâ åãî, íàéäåì çíà÷åíèÿ x è
y
:
22
19,
28
xxyy
xy
++=
+=
⇔
22
19,
82
xxyy
xy
++=
=−
⇔
⇔
22
(8 2 ) (8 2 ) 19,
82
yyyy
xy
−+−+=
=−
⇔
⇔
2
324450,
82
yy
xy
−+=
=−
⇔
2
8150,
82
yy
xy
−+=
=−
⇔
⇔
=
=
2
,3
x
y
èëè
−=
=
.2
,5
x
y
Îòâåò: (2; 3), (2; 5).
Îäíîðîäíûå ñèñòåìû
Ñèñòåìû óðàâíåíèé âòîðîé ñòåïåíè, õîòÿ áû îäíî èç êîòîðûõ
ÿâëÿåòñÿ îäíîðîäíûì óðàâíåíèåì, ðåøàþòñÿ ìåòîäîì ïîäñòàíîâ-
êè ïî ñëåäóþùåé ñõåìå:
22
22
111
1
,
0,
0
Ax Bxy Cy D
Ax Bxy Cy
C
++=
++=
≠
⇔
22
1
22
2
,
,
.
Ax Bxy Cy D
xky
Ax Bxy Cy D
xky
++=
=
++=
=
ãäå
1
k
,
2
k
êîðíè óðàâíåíèÿ
2
111
0
Ak Bk C
++=
.
Ïðèìåð 10. Ðåøèòå ñèñòåìó óðàâíåíèé
=−+
=+−
.732
,353
22
22
yxyx
yxyx
Ðåøåíèå. Óìíîæèì ïåðâîå óðàâíåíèå íà 7, à âòîðîå íà 3, ïîñëå
âû÷èòàíèÿ ïîëó÷èì:
04424
22
=+−
yxyx
.
Îòêóäà
04424
2
=+
−
y
x
y
x
. Äàëåå, âîñïîëüçîâàâøèñü çàìå-
íîé
k
y
x
=
, ïîëó÷èì êâàäðàòíîå óðàâíåíèå
04424
2
=+−
kk
, êîð-
íè êîòîðîãî
22
1
=
k
è
2
2
=
k
.
=−
=
−
+
12
,3
22
yx
yx
yx
è
=−
=
−
+
.12
,
3
1
22
yx
yx
yx
Óêàçàíèå. Äàëåå âîñïîëüçóéòåñü ìåòîäîì ïîäñòàíîâêè.
Îòâåò: (4; 2), (4; 2), (4; 2), (4; 2).
Ïðèìåð 8. Ðåøèòå ñèñòåìó óðàâíåíèé
=−
=−
.6
,
6
111
22
yxxy
yx
Ðåøåíèå. Ïðåîáðàçóåì ñèñòåìó ê âèäó
=−
=
−
.6
)
(
,
6
1
xyxy
xy
xy
Ââåäåì íîâûå ïåðåìåííûå:
xyu
−=
,
xyv
=
.
Ïîëó÷èì áîëåå ïðîñòóþ ñèñòåìó:
=
=
6
,
6
1
uv
v
u
⇔
=
=
6
,6
uv
uv
⇔
=
=
1
,6
2
u
uv
⇔
=
=
1
,6
u
v
èëè
−=
−=
.1
,6
u
v
Îñòàëîñü ðåøèòü ñîâîêóïíîñòü äâóõ ñèñòåì:
=−
=
1
,6
xy
yx
è
−=−
−=
.1
,6
xy
yx
Âòîðàÿ ñèñòåìà ðåøåíèé íå èìååò, à ïåðâóþ ëåãêî ðåøèòü ìå-
òîäîì ïîäñòàíîâêè.
Îòâåò: (2; 3), (3; 2).
Ñèñòåìû óðàâíåíèé, îäíî èç êîòîðûõ ÿâëÿåòñÿ
ëèíåéíûì óðàâíåíèåì
Ñèñòåìû óðàâíåíèé, èç êîòîðûõ îäíî ïåðâîé ñòåïåíè, à äðóãîå
êâàäðàòíîå, êàê ïðàâèëî, ðåøàþò ñ ïîìîùüþ ìåòîäà ïîäñòàíîâêè.
Ïðèìåð 9. Ðåøèòå ñèñòåìó óðàâíåíèé
=+
=++
.82
,19
22
yx
yxyx
Ðåøåíèå. Èç âòîðîãî óðàâíåíèÿ ñèñòåìû âûðàçèì îäíó ïåðå-
ìåííóþ ÷åðåç äðóãóþ, çàòåì ïîäñòàâèì ïîëó÷åííîå âûðàæåíèå â
52
53
Ìåòîäû ðåøåíèÿ ñèñòåì óðàâíåíèé
Ëåêöèÿ 3
Íàéäåì êîðíè êâàäðàòíîãî óðàâíåíèÿ
0210
2
=−+
zz
. Êîðíè
êâàäðàòíîãî óðàâíåíèÿ
14
1
=
z
,
15
2
−
z
.
Îñòàëîñü ðåøèòü ñèñòåìû
−=−
=
153
,142
y
x
è
=−
−=
.143
,152
y
x
Îòâåò: (7; 5),
114
7;
23
−−
.
Ñèììåòðè÷åñêèå ñèñòåìû
Ñèñòåìó óðàâíåíèé âèäà
=
=
0
)
,
(
,0
)
,
(
yxg
yxf
,
ãäå
),( yxf
,
)
,
(
yxg
ñèì-
ìåòðè÷åñêèå ìíîãî÷ëåíû, ðåøàþò ñ ïîìîùüþ çàìåíû:
ayx
=+
,
bxy
=
. Ñìûñë òàêîé çàìåíû çàêëþ÷àåòñÿ â òîì, ÷òî ñòåïåíè óðàâ-
íåíèé, âõîäÿùèõ â ñèñòåìó ïîñëå çàìåíû, êàê ïðàâèëî, óìåíüøà-
þòñÿ: îäíî÷ëåí âòîðîé ñòåïåíè õó ïåðåõîäèò â îäíî÷ëåí ïåðâîé
ñòåïåíè.
Ïðèìåð 13. Ðåøèòå ñèñòåìó óðàâíåíèé
=+
=+
.5
,35
33
yx
yx
Ðåøåíèå. Âîñïîëüçóåìñÿ çàìåíîé:
ayx
=+
,
bxy =
.
Ïîñêîëüêó
)
(
3
)
(
333
yxxyyxyx
+−+=+
, òî äàííóþ ñèñòåìó
ìîæíî ïåðåïèñàòü â ñëåäóþùåì âèäå:
=
=−
.5
,353
3
a
aba
⇔
=
=−
.5
,3515125
a
b
⇔
=
=
.5
,6
a
b
Äàëåå ñìîòðè ïðèìåð 11.
Îòâåò: (2; 3), (3; 2)
Ïðèìåð 14. Ðåøèòå ñèñòåìó óðàâíåíèé
=++
=++
.5
,17
3333
xyyx
yyxx
Ðåøåíèå. Âîñïîëüçóåìñÿ çàìåíîé:
ayx
=+
,
bxy
=
.
Òàêèì îáðàçîì, óðàâíåíèå
04424
22
=+−
yxyx
ðàâíîñèëüíî
ñîâîêóïíîñòè óðàâíåíèé
yx
22=
è
yx
2=
. Òàêèì îáðàçîì
22
22
353,
237
xxyy
xxy y
−+=
+− =
⇔
22
22
353,
24 44 0
xxyy
xxyy
−+=
−+=
⇔
⇔
22
22
353,
22
353,
2.
xxyy
xy
xxyy
xy
−+=
=
−+=
=
Äàëåå ðåøèì êàæäóþ èç ïîëó÷åííûõ ñèñòåì ìåòîäîì ïîäñòà-
íîâêè.
Îòâåò:
141
1
;
141
22
,
−−
141
1
;
141
22
, (2; 1), (2; 1).
Èñïîëüçîâàíèå òåîðåìû Âèåòà
Ñèñòåìó óðàâíåíèé âèäà
,
xy a
xy b
+=
=
ìîæíî ñâåñòè ê êâàäðàòíî-
ìó óðàâíåíèþ
0
2
=+−
bazz
.
Ïðèìåð 11. Ðåøèòå ñèñòåìó óðàâíåíèé
=
=+
.6
,5
xy
yx
Ðåøåíèå. Íàéäåì êîðíè êâàäðàòíîãî óðàâíåíèÿ
065
2
=+−
zz
.
Ïîëó÷èì:
2
1
=
z
,
3
2
=
z
.
Îòâåò: (2; 3), (3; 2).
Ïðèìåð 12. Ðåøèòå ñèñòåìó óðàâíåíèé
=
−=−
.35
,132
xy
yx
Ðåøåíèå. Âîñïîëüçóåìñÿ çàìåíîé:
mx
=2
,
ny
=−3
.
Ïîëó÷èì ñèñòåìó
−=
−=+
.210
,1
mn
nm

54
55
Ìåòîäû ðåøåíèÿ ñèñòåì óðàâíåíèé
Ëåêöèÿ 3
Åùå íåñêîëüêî ïðèìåðîâ
Ïðèìåð 16. Ðåøèòå ñèñòåìó óðàâíåíèé
=−
=+
.6
,24
3
3
x
y
xy
y
x
xy
Ðåøåíèå. Çàìåòèì, ÷òî ïîñêîëüêó
0≠
xy
, òî, ïåðåìíîæèâ óðàâíå-
íèÿ, ïîëó÷èì óðàâíåíèå-ñëåäñòâèå èç äàííîé ñèñòåìû:
()()
22
624
yxxyxy
=−+
, ÷òî ðàâíîñèëüíî
8=xy
.
Ïðèñîåäèíèì óðàâíåíèå
8=
xy
ê èñõîäíîé ñèñòåìå è ðåøèì
ïîëó÷åííóþ ñèñòåìó ìåòîäîì ïîäñòàíîâêè.
Îòâåò: (4; 2), (4; 2).
Ïðèìåð 17. Ðåøèòå ñèñòåìó óðàâíåíèé
=+−−+−
=+−−−+
.020617523
,0416382510
22
22
yxxyyx
yxxyyx
Ðåøåíèå. Ïðåäñòàâèì ïåðâîå óðàâíåíèå ñèñòåìû êàê êâàäðàò-
íîå îòíîñèòåëüíî õ. Ïîëó÷èì:
22
10 2( 19) 5 6 41 0
xyxyy
−+ +−+=
.
Óðàâíåíèå èìååò êîðíè, åñëè
()
0
)
4165
(
1019
2
2
≥+−−+
yyy
,
îòêóäà
0499849
2
≥−+−
yy
è
0
)
1
(
49
2
≥−−
y
, òî åñòü
1=y
.
Ïîñëå ïîäñòàíîâêè âî âòîðîå óðàâíåíèå ñèñòåìû ïîëó÷èì:
044
2
=+−
xx
. Îñòàåòñÿ ïðîâåðèòü, ÷òî ïàðà ÷èñåë (2; 1) ÿâëÿåò-
ñÿ ðåøåíèåì ñèñòåìû. Ñäåëàéòå ýòî ñàìîñòîÿòåëüíî.
Äëÿ ñèñòåì òðåõ (è áîëåå) óðàâíåíèé ñ òðåìÿ (è áîëåå) ïåðåìåí-
íûìè ïðèìåíÿþòñÿ ìåòîäû ðåøåíèÿ è ñïðàâåäëèâû ðåçóëüòàòû,
àíàëîãè÷íûå òåì, ÷òî áûëè ðàññìîòðåíû äëÿ ñèñòåì äâóõ óðàâíå-
íèé ñ äâóìÿ ïåðåìåííûìè.
Ïðèìåð 18. Ðåøèòå ñèñòåìó óðàâíåíèé
=−+++
=++
=++
.9
)
1
(
)
2
(
,132
,2
222
zyx
zyx
zyx
33
317,
5
aabb
ab
−+=
+=
⇔
33
33
317,
3( )125,
5
aabb
ab abab
ab
−+=
++ +=
+=
⇔
⇔
33
33
317,
15 125,
5
aabb
ab ab
ab
−+=
++ =
+=
⇔
18 108,
5
ab
ab
=
+=
⇔
6,
5
ab
ab
=
+=
⇔
2,
3
3,
2.
a
b
a
b
=
=
=
=
Îñòàëîñü ðåøèòü ñèñòåìó
3,
2
xy
xy
+=
=
èëè
=
=+
.3
,2
xy
yx
Ñäåëàéòå ýòî ñàìîñòîÿòåëüíî.
Îòâåò: (1; 2), (2; 1).
Èíîãäà áûâàåò, ÷òî ñèñòåìà, ñîñòîÿùàÿ èç íåñèììåòðè÷åñêèõ
óðàâíåíèé, ìîæåò áûòü ñâåäåíà ê ñèñòåìå ñèììåòðè÷åñêèõ óðàâ-
íåíèé ïîäõîäÿùåé çàìåíîé.
Ïðèìåð 15. Ðåøèòå ñèñòåìó
=−
=−
.8
,2
33
yx
yx
Ðåøåíèå. Ïóñòü
yp
−=
. Ïåðåïèøåì ñèñòåìó â âèäå
=+
=+
.8
,2
33
px
px
Òåïåðü ñèñòåìà ñèììåòðè÷íà. Âîñïîëüçîâàâøèñü ñòàíäàðòíîé
çàìåíîé
apx
=+
,
bxp
=
ïîëó÷èì:
3
2,
38
a
aab
=
−=
⇔
=
=
.06
,2
b
a
Ñëåäîâàòåëüíî,
0=
xp
.
Ðàññìîòðèì äâà ñëó÷àÿ
1)
0=
x
,
2−=
y
;
2)
0=
p
, òîãäà
0=
y
,
2=
x
.
Îòâåò: (0; 2), (2; 0).
56
57
Ìåòîäû ðåøåíèÿ ñèñòåì óðàâíåíèé
Ëåêöèÿ 3
Ïðèìåð 20. Ðåøèòå ñèñòåìó óðàâíåíèé
=
+
=
+
=
+
.3
,4
,5
zx
zx
zy
yz
yx
xy
Ðåøåíèå. Çäåñü òîæå ïîìîæåò ñèììåòðèÿ:
1
,
5
1
,
4
1
3
xy
xy
yz
yz
zx
xz
+
=
+
=
+
=
⇔
111
,
5
11 1
,
4
11 1
3
xy
yz
xz
+=
+=
+=
⇔
111
,
5
11 1
,
4
111
,
3
111 47
120
xy
yz
xz
xyz
+=
+=
+=
++=
⇔
⇔
1471
,
120 5
1471
,
120 4
1471
,
120 3
111 47
120
z
x
y
xyz
=−
=−
=−
++=
⇔
123
,
120
117
,
120
17
,
120
111 47
.
120
z
x
y
xyz
=
=
=
++=
Îòâåò:
120 120 120
;;
17 7 23
.
Ïðèìåð 21. Ðåøèòå ñèñòåìó óðàâíåíèé
22
232 2
2222
2100,
93,
218 10.
zyz xy
yz z x y xy
yxyzxz
++ =
++ =
+−=
Ðåøåíèå. Âû÷òåì ïåðâîå óðàâíåíèå èç âòîðîãî, ïîëó÷èì ðàâ-
íîñèëüíóþ ñèñòåìó:
222
21,
2,
23 1,
(2)(1)9
xy
xyz
xyz
xy z
=− −
++=
++=
++ +− =
⇔
222
21,
3,
23 1,
(2)(1)9
xy
zy
xyz
xy z
=− −
=+
++=
++ +− =
⇔
⇔
222
21,
3,
23 1,
(2 1) ( 2) ( 2) 9
xy
zy
xyz
yyy
=− −
=+
++=
+++++=
⇔
=+
=++
+=
−−=
.0
)
2
(
,132
,3
,12
yy
zyx
yz
yx
Ïîäñòàâèâ
0=
y
â ïåðâîå è âòîðîå óðàâíåíèÿ, ïîëó÷èì:
1−=
x
,
3=
z
.
Åñëè
2=y
, òî
5−=
x
,
5=
z
.
Îòâåò: (5; 2; 5), (1; 0; 3).
Ïðèìåð 19. Ðåøèòå ñèñòåìó óðàâíåíèé
=
=
=
.2
,9
,2
zx
yz
xy
Ñèììåòðè÷íàÿ ñòðóêòóðà óðàâíåíèé ïîäñêàçûâàåò ñëåäóþùèé
ïðèåì. Ïåðåìíîæèì óðàâíåíèÿ ñèñòåìû:
36
222
=
zyx
. Ñëåäîâà-
òåëüíî,
6±=xyz
.
Ðàññìîòðèì ñëó÷àè:
1)
⇔
2)
6,
2,
9,
2
xyz
xy
yz
zx
=−
=
=
=
⇔
3,
2
,
3
3.
z
x
y
=−
=−
=−
Îòâåò:
22
;3;3 , ;3;3
33
.
Íàâûê ðåøåíèÿ ñèñòåì óðàâíåíèé ïðèõîäèò ïîñòåïåííî. Ðàñ-
ñìîòðèì íåñêîëüêî áîëåå òðóäíûõ ïðèìåðîâ.
3,
2
,
3
3;
z
x
y
=
=
=
6,
2,
9,
2
xyz
xy
yz
zx
=
=
=
=

58
59
Ìåòîäû ðåøåíèÿ ñèñòåì óðàâíåíèé
Ëåêöèÿ 3
3)
22
1,
2100,
3
x
zyz xy
zy xy
=−
++ =
+=−
⇔
2
1,
2100,
3
x
zyz y
zy y
=−
++ =
+=
⇔
⇔
2
1,
2100,
2.
x
zyz y
zy
=−
++ =
=
Ïîëó÷èì äâà ðåøåíèÿ:
1−==
yx
,
2−=
z
è
1−=x
,
0==
zy
.
Îòâåò: (1; 1; 2), (à; 0; 0), ãäå à ïðîèçâîëüíîå äåéñòâè-
òåëüíîå ÷èñëî.
Óïðàæíåíèÿ äëÿ ñàìîñòîÿòåëüíîé ðàáîòû
Ðåøèòå ñèñòåìó óðàâíåíèé ìåòîäîì ïîäñòàíîâêè (12).
1.
=++−
−=+
.0199
,1943
22
yxyx
yx
2.
=+
+=+
.6
)
,2
(
2
22
yx
xyyx
Ðåøèòå ñèñòåìó óðàâíåíèé ìåòîäîì ñëîæåíèÿ (34).
3.
=+
=+
.10
,15
2
2
xyy
xyx
4.
−=−+
−=++
.11
,3233
xyyx
xyyx
Ðåøèòå ñèñòåìó óðàâíåíèé ìåòîäîì çàìåíû (57).
5.
=
−
−
−
=
−
+
−
.
18
1
2
1
2
2
,
2
1
2
3
2
2
yxyx
yxyx
6.
=−+
=+−
.622
,332
22
22
yxyx
yxyx
7.
=
+
−
=
+
+−
.
3
1
53
32
,
3
4
53
1
32
yx
yx
yx
yx
Ðåøèòå ñèììåòðè÷åñêóþ ñèñòåìó (810).
8.
=++
++=+
.69
,102
22
yxxy
yxyx
9.
=+
=+
.4
,8
22
33
yx
yx
Ðåøåíèå. Óìíîæèì ïåðâîå óðàâíåíèå ñèñòåìû íà z, âòîðîå
íà
y
6
, òðåòüå íà
y
. Ïîëó÷èì:
32 2
2233 3
332 2
2100,
6 6 54 18 ,
218 10.
zyz xyz
yz yz xy xy
yxyzyxzy
++ =
++ =
+−=
Ñëîæèì âñå òðè óðàâíåíèÿ:
333223
542662
yxyzyyzz
−=+++
,
33
)
3
(
)
(
xyyz
−=+
,
xyyz 3−=+
,
)
13
(
+−=
xyz
.
Ïîñëåäíåå óðàâíåíèå ÿâëÿåòñÿ ñëåäñòâèåì èñõîäíîé ñèñòåìû.
Çàïèøåì ñèñòåìó óðàâíåíèé, ðàâíîñèëüíóþ èñõîäíîé ñèñòåìå:
22
232 2
2222
2100,
93,
218 10,
(3 1).
zyz xy
yz z x y xy
yxyz xz
zyx
++ =
++ =
+−=
=− +
Ïîäñòàâèì âî âòîðîå óðàâíåíèå
)
13
(
+−=
xyz
:
223222
39
)
13
(
)
13
(
xyyxxyxy
=++++−
,
0
)
3916913
(
322
=−++++−−
xxxxxy
,
0
)
1
(
9
22
=+
xyx
.
Îñòàëîñü ðàññìîòðåòü ñëó÷àè:
1)
22
0,
2100,
3
x
zyz xy
zy xy
=
++ =
+=−
⇔
2
0,
20,
0
x
zyz
zy
=
+=
+=
⇔
2
0,
20,
.
x
zyz
yz
=
+=
=−
Ïîëó÷èì ðåøåíèå:
0===
zyx
.
2)
22
0,
2100,
3
y
zyz xy
zy xy
=
++ =
+=−
⇔
2
0,
20,
3
y
z
zy xy
=
=
+=−
⇔
0,
0,
030.
y
z
x
=
=
=− ⋅
Ïîëó÷èì ðåøåíèå:
x
ïðîèçâîëüíîå äåéñòâèòåëüíîå ÷èñëî,
0==
zy
.
