Чулков П.В. Уравнения и неравенства в школьном курсе математики
Подождите немного. Документ загружается.

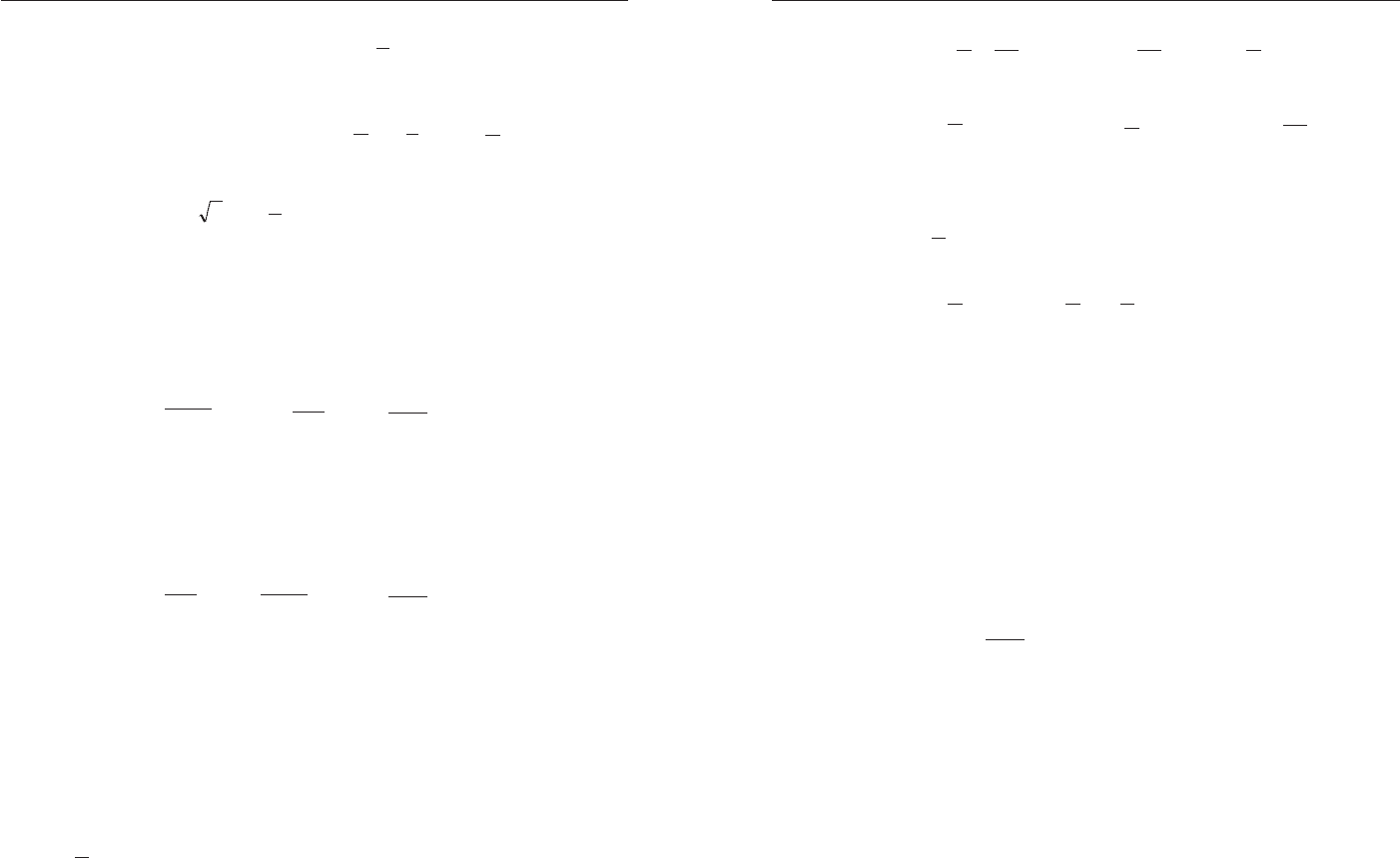
20
21
Îáùèå ñâåäåíèÿ îá óðàâíåíèÿõ, íåðàâåíñòâàõ è èõ ñèñòåìàõ
Ëåêöèÿ 1
Êîðíè êâàäðàòíîãî óðàâíåíèÿ:
2
5
1
=
t
è
4
2
−=
t
.
Òàêèì îáðàçîì, èñõîäíîå óðàâíåíèå ÷åòâåðòîé ñòåïåíè ðàâíî-
ñèëüíî ñîâîêóïíîñòè óðàâíåíèé
2
1
2
1
=+
x
x
è
4
1
−=+
x
x
. Ðåøèâ
óðàâíåíèÿ, ïîëó÷èì åùå ÷åòûðå êîðíÿ èñõîäíîãî óðàâíåíèÿ.
Îòâåò: 1,
32 ±−
, 2,
2
1
.
Âîçâðàòíûå óðàâíåíèÿ
Óðàâíåíèÿ âèäà
0
1221
12
1
12
0
=+++++++
++
++
nn
n
n
n
n
nn
axaxaxaxaxa
KK
íàçûâàþò âîçâðàòíûìè óðàâíåíèÿìè íå÷åòíîé ñòåïåíè, åñëè
1
0
12
+
+
λ=
n
n
a
a
,
n
n
a
a
λ=
1
2
,
λ=
+
n
n
a
a
1
,
ãäå
λ
íåêîòîðîå äåéñòâèòåëüíîå ÷èñëî.
Óðàâíåíèÿ âèäà
0
212
1
1
12
1
2
0
=+++++++
−
+
−
−
nn
n
n
n
n
nn
axaxaxaxaxa
KK
íàçûâàþò âîçâðàòíûìè óðàâíåíèÿìè ÷åòíîé ñòåïåíè, åñëè
n
n
a
a
λ=
0
2
,
1
1
12
−
−
λ=
n
n
a
a
,
λ=
−
+
1
1
n
n
a
a
,
ãäå
λ
íåêîòîðîå äåéñòâèòåëüíîå ÷èñëî.
Òàêèì îáðàçîì, îòíîøåíèÿ êîýôôèöèåíòîâ âîçâðàòíîãî óðàâ-
íåíèÿ, ðàâíîîòñòîÿùèõ îò êîíöîâ, ïðîïîðöèîíàëüíû ñòåïåíÿì
íåêîòîðîãî ôèêñèðîâàííîãî ÷èñëà.
Âîçâðàòíûå óðàâíåíèÿ îáëàäàþò ñëåäóþùèìè ñâîéñòâàìè:
1) âîçâðàòíîå óðàâíåíèå íå÷åòíîé ñòåïåíè èìååò êîðåíü
λ−=
x
,
â ÷åì ìîæíî óáåäèòüñÿ ïîäñòàíîâêîé;
2) óðàâíåíèå ÷åòíîé ñòåïåíè 2n ñ ïîìîùüþ ïîäñòàíîâêè
x
xv
λ
+=
ñâîäèòñÿ ê óðàâíåíèþ ñòåïåíè n.
Ïðèìåð 23. Ðåøèòå óðàâíåíèå
0124423
234
=+−+−
xxxx
.
Ðåøåíèå. Ðàçäåëèì îáå ÷àñòè óðàâíåíèÿ íà õ
2
è ñãðóïïèðóåì
÷ëåíû óðàâíåíèÿ:
0
124
423
2
2
=+−+−
x
x
xx
,
04
2
2
4
3
2
2
=+
+−
+
x
x
x
x
.
Îáîçíà÷èì
p
x
x
=+
2
, òîãäà
2
2
2
p
x
x
=
+
è
4
4
2
2
2
−=+
p
x
x
.
Ïîëó÷èì óðàâíåíèå
042
)
4
(
3
2
=+−−
pp
, îòêóäà
0823
2
=−−
pp
,
è
2
1
=
p
,
3
4
2
−=
p
.
Óðàâíåíèÿ
2
2
=+
x
x
è
3
42
−=+
x
x
êîðíåé íå èìåþò, ñëåäîâà-
òåëüíî, èñõîäíîå óðàâíåíèå òàêæå íå èìååò êîðíåé.
Îòâåò: êîðíåé íåò.
Îäíîðîäíûå óðàâíåíèÿ
Óðàâíåíèå âèäà
() () ()() ()
1
01
() () () () () () 0
nn nkk n
kn
a ux a ux vx a ux vx a vx
−−
+++ ++=
KK
íàçûâàþò îäíîðîäíûì óðàâíåíèåì ñòåïåíè n îòíîñèòåëüíî
)
(
xu
è
)
(
xv
.
Ïîäåëèâ îáå ÷àñòè îäíîðîäíîãî óðàâíåíèÿ íà
()
n
xv
)
(
, ìîæíî ñ
ïîìîùüþ çàìåíû
)
(
)
(
xv
xu
p
=
ïîëó÷èòü óðàâíåíèå
0
1
10
=+++++
−−
n
kn
k
nn
apapapa
KK
,
÷òî ïîçâîëÿåò óïðîñòèòü èñõîäíîå óðàâíåíèå. Ñëó÷àé
0)( =xv
íå-
îáõîäèìî ðàññìîòðåòü îòäåëüíî.
Ïðèìåð 24. Ðåøèòå óðàâíåíèå
0
)
1
(
2
)
1
)(
2
(
)
1
(
)
2
(
2222
=−−−−−+−
xxxxx
.
Ðåøåíèå. Ïóñòü
)
1
)(
2
(
+−=
xxu
,
1−=
xv
, òîãäà èñõîäíîå óðàâ-
íåíèå ìîæíî çàïèñàòü â âèäå
02
22
=−−
vuvu
.
Ðàññìîòðèì ñëó÷àè:
1) Ïóñòü
0=
v
, òîãäà
1=
x
. Íî ïðîâåðêà ïîêàçûâàåò, ÷òî 1 íå
ÿâëÿåòñÿ êîðíåì èñõîäíîãî óðàâíåíèÿ.
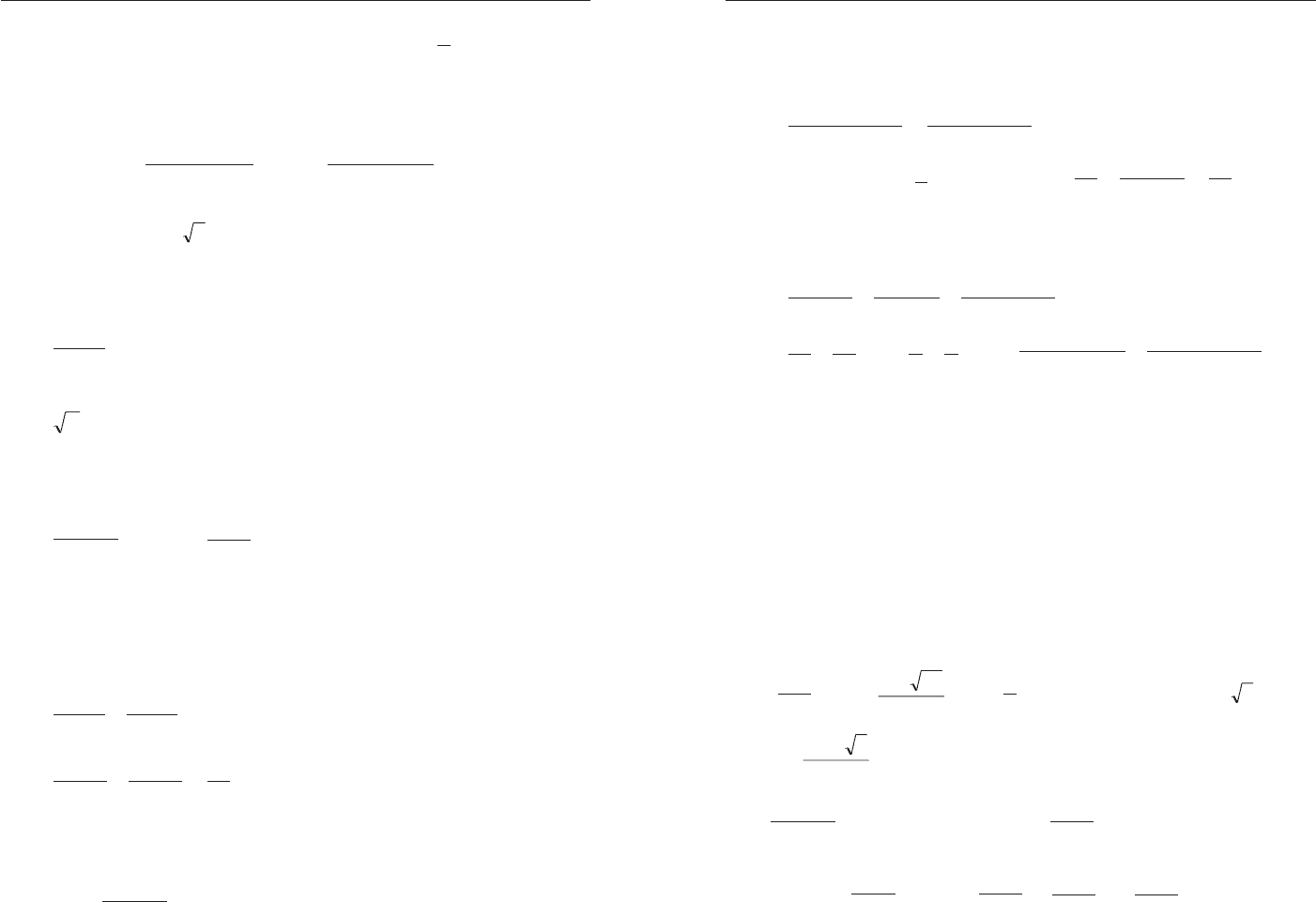
22
23
Îáùèå ñâåäåíèÿ îá óðàâíåíèÿõ, íåðàâåíñòâàõ è èõ ñèñòåìàõ
Ëåêöèÿ 1
2) Ïóñòü
0≠v
, òîãäà ñ ïîìîùüþ çàìåíû
v
u
p
=
ïîëó÷èì óðàâ-
íåíèå
02
2
=−−
pp
, îòêóäà
1
1
−=
p
,
2
2
=
p
.
Îñòàëîñü ðåøèòü ñîâîêóïíîñòü óðàâíåíèé
1
1
)
1
)(
2
(
−=
−
+−
x
xx
è
2
1
)
1
)(
2
(
=
−
+−
x
xx
,
êàæäîå èç êîòîðûõ ñâîäèòñÿ ê êâàäðàòíîìó óðàâíåíèþ.
Îòâåò:
0
,
3
,
3±
.
Óïðàæíåíèÿ äëÿ ñàìîñòîÿòåëüíîé ðàáîòû
Ðàâíîñèëüíû ëè óðàâíåíèÿ (13).
1.
0
1
1
2
=
−
−
x
x
è
01
2
=−
x
.
2.
02
2
=+
xx
è
0)2(
2
=+
xx
.
3.
1
−=
x
è
03
2
=+
x
?
Êàêîå èç äâóõ óðàâíåíèé, ÿâëÿåòñÿ ñëåäñòâèåì äðóãîãî (45).
4.
9
2
=
x
èëè x = 3.
5.
0
9
)
3
(
2
2
=
−
−
x
x
èëè
0
3
3
=
+
−
x
x
?
Ðåøèòå óðàâíåíèå ìåòîäîì ðàçëîæåíèÿ íà ìíîæèòåëè (67).
6.
06116
23
=−+−
xxx
.
7.
)
4
)(
3
)(
2
)(
1
(
)
4
)(
3
)(
2
)(
1
(
++++=−−−−
xxxxxxxx
.
Ðåøèòå äðîáíî-ðàöèîíàëüíîå óðàâíåíèå (89).
8.
23
3
1
4
1
22
=
+
−
−
−
+
x
x
x
x
.
9.
10
29
1
32
32
1
2
2
=
+
+
+
+
+
x
x
x
x
.
Ðåøèòå óðàâíåíèå ìåòîäîì çàìåíû ïåðåìåííûõ (1019).
10.
089
36
=+−
xx
. 11.
015
)
4
(
8
)
4
(
2222
=++++++
xxxxxx
.
12.
27
)
3
(
9
2
2
2
=
+
+
x
x
x
. 13.
10
)
8
)(
5
)(
3
(
=+++
xxxx
.
14.
2
40)6)(1)(3)(2(
xxxxx
=+−−+
.
15.
01454
234
=+−+−
xxxx
.
16.
012101453
234
=+−−+
xxxx
.
17.
156
3
156
1510
22
2
+−
=
+−
+−
xx
x
xx
xx
.
18.
8
1
)
1
(
44
=−+
xx
. 19.
9
10
)
2
(
11
22
=
+
+
xx
.
Ðåøèòå óðàâíåíèå ìåòîäîì çàìåíû ïåðåìåííûõ (2024).
20.
81
)
3
(
2
)
6
(
222
=−−−
xxx
. 21.
6)4)(3)(2( =−−− xxx
.
22.
0
23
3
)
2
(
2
)
1
(
1
222
=
++
−
+
+
+
xxxx
.
23.
−=+
x
x
x
x
4
3
10
48
3
2
2
. 24.
1
7104
3
784
4
22
=
+−
+
+−
xx
x
xx
x
.
Îòâåòû, óêàçàíèÿ, ðåøåíèÿ
1. Íåò. 2. Äà. 3. Äà. 4. Ïåðâîå. 5. Âòîðîå. 6. 1; 2; 3. 7. 0. Ïåðå-
ìíîæèì ïîïàðíî ïåðâûå è ÷åòâåðòûå, à òàêæå âòîðûå è òðåòüè
ñêîáêè â ëåâîé è ïðàâîé ÷àñòÿõ óðàâíåíèÿ:
)
65
)(
45
(
)
65
)(
45
(
2222
++++=+−+−
xxxxxxxx
.
Äàëåå ïðåäñòàâèì ëåâóþ è ïðàâóþ ÷àñòè óðàâíåíèÿ êàê ðàç-
íîñòü êâàäðàòîâ:
1
)
55
(
1
)
55
(
2222
−++=−+−
xxxx
,
îòêóäà ïîëó÷èì:
0
)
55
(
)
55
(
2222
=++−+−
xxxx
è
0
)
102
(
10
2
=+−
xx
.
8.
16
55−
; 5. 9.
2
515 ±
; 1;
5
4
−
. 10. 1; 2. 11. 2;
53 ±−
.
12.
2
533 ±
. Ïðèáàâèì ê îáåèì ÷àñòÿì óðàâíåíèÿ
27
)
3
(
9
2
2
2
=
+
+
x
x
x
âûðàæåíèå
3
3
2
+
⋅−
x
x
x
. Ïîëó÷èì:
3
6
27
3
3
2
2
+
−=
+
−
x
x
x
x
x
,
027
3
6
3
2
2
2
=−
+
+
+
x
x
x
x
.
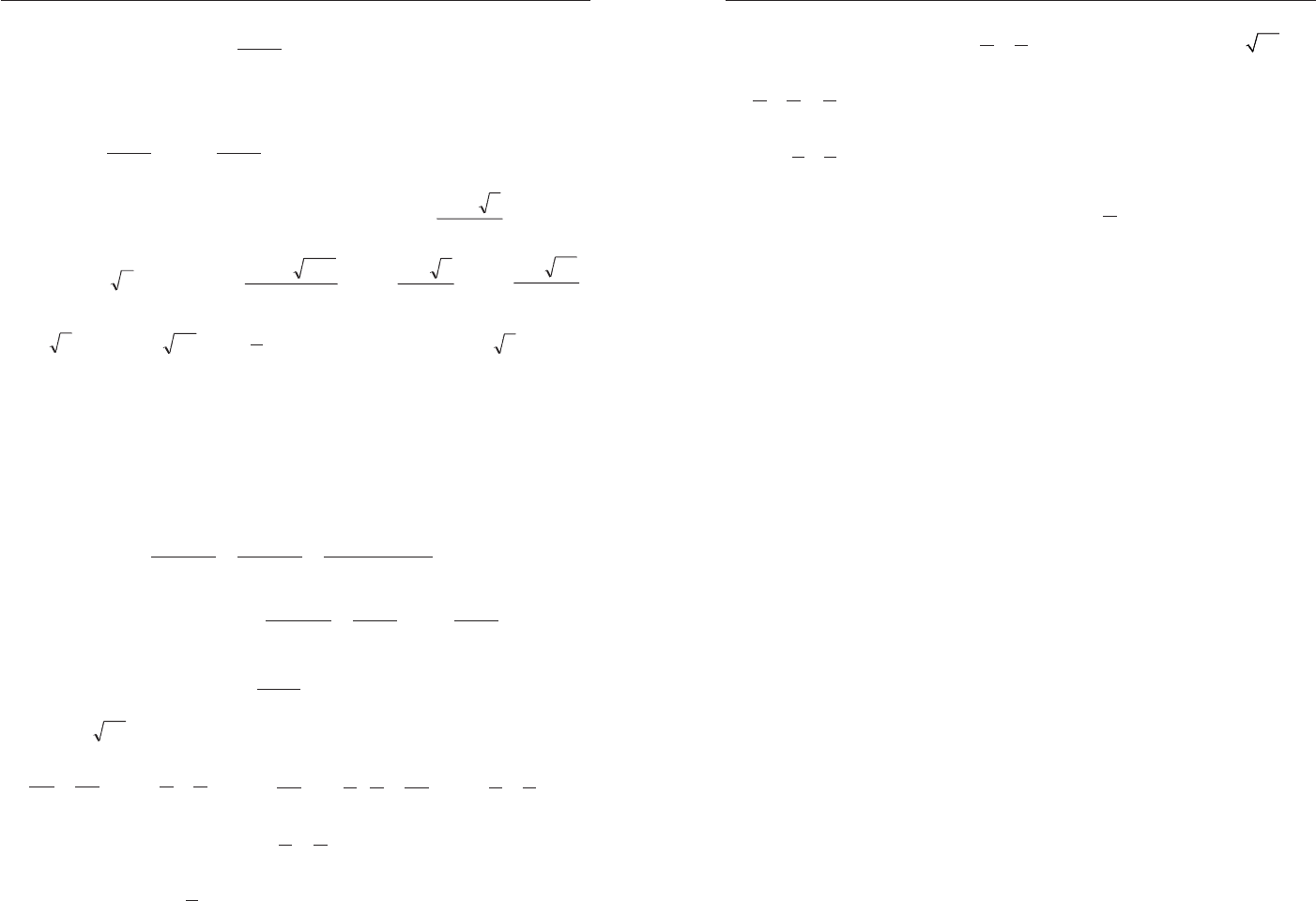
24
25
Îáùèå ñâåäåíèÿ îá óðàâíåíèÿõ, íåðàâåíñòâàõ è èõ ñèñòåìàõ
Ëåêöèÿ 1
Âûïîëíèì çàìåíó
3
2
+
=
x
x
y
. Ïîëó÷èì êâàäðàòíîå óðàâíåíèå
0276
2
=−+
yy
, îòêóäà
9
1
−=
y
,
3
2
=
y
. Ðåøèì ñîâîêóïíîñòü
óðàâíåíèé
9
3
2
−=
+
x
x
,
3
3
2
=
+
x
x
. Ïåðâîå èç óðàâíåíèé ñîâîêóï-
íîñòè ðåøåíèé íå èìååò, à âòîðîå èìååò êîðíè
2
533 ±
.
13.
64 ±−
. 14. 1; 6;
2
1059 ±−
. 15.
2
53 ±
. 16.
6
731 ±
,
31 ±−
. 17.
347
±
. 18.
2
1
. 19. 3 è 1. 20. 3 è
523 ±
.
21. 5. Óêàçàíèå. Ïóñòü
3−=
xt
, òîãäà
3+=
tx
è ïîñëå ïîä-
ñòàíîâêè èñõîäíîå óðàâíåíèå ïðèíèìàåò âèä:
6
)
1
(
2
=−
tt
, îòêóäà
06
3
=−−
tt
. Ðàçëîæèì ïîëó÷åííîå óðàâíåíèå íà ìíîæèòåëè:
063422
223
=−+−+−
ttttt
,
0
)
32
)(
2
(
2
=++−
ttt
, îòêóäà
2=t
.
22. 0. Óêàçàíèå. Ïðåîáðàçóåì óðàâíåíèå ê âèäó
0
)
2
)(
1
(
3
)
2
(
2
)
1
(
1
22
=
++
−
+
+
+
xx
xx
,
÷òî ðàâíîñèëüíî óðàâíåíèþ
02
1
2
3
1
2
)
2
(
1
2
2
=
+
+
+
−
+
+
+
x
x
x
x
x
.
Âîñïîëüçóåìñÿ çàìåíîé
1
2
+
+
=
x
x
y
.
23.
213 ±
, 2, 6. Ðåøåíèå. Äàííîå óðàâíåíèå ðàâíîñèëüíî:
−=
+
x
x
x
x
4
3
10
16
9
3
2
2
⇔
8
4
3
10
164
3
2
9
3
2
2
−
−=
+⋅⋅−
x
x
x
x
xx
.
Âîñïîëüçóåìñÿ çàìåíîé
x
x
y
4
3
−=
. Ïîëó÷èì:
08103
2
=+−
yy
,
îòêóäà
2
1
=
y
,
3
4
2
=
y
.
Ðåøèì óðàâíåíèÿ: 1)
2
4
3
=−
x
x
, îòêóäà
1,2
321
x
=±
, è
2)
3
44
3
=−
x
x
, îòêóäà
2
3
−=
x
,
6
4
=
x
.
24.
2
1
,
2
7
. Óêàçàíèå. Ðàçäåëèòå íà õ ÷èñëèòåëè è çíàìåíàòåëè
äðîáåé. Âîñïîëüçóéòåñü çàìåíîé
10
7
4 −+=
x
xy
.

26
Ëåêöèÿ 1
27
Ìåòîäû ðåøåíèÿ íåðàâåíñòâ
(2.5.) Îáëàñòüþ äîïóñòèìûõ çíà÷åíèé íåðàâåíñòâà (ïðèíÿòîå
ñîêðàùåíèå ÎÄÇ) íàçûâàþò ìíîæåñòâî, íà êîòîðîì îïðåäåëå-
íû îáå ôóíêöèè
)
(
xf
è
)
(
xg
.
(2.6.) Íåðàâåíñòâà ðàâíîñèëüíû, åñëè îíè èìåþò îäíî è òî æå
ìíîæåñòâî ðåøåíèé.  ÷àñòíîñòè, åñëè íåðàâåíñòâà íå èìåþò ðå-
øåíèé, òî îíè ðàâíîñèëüíû.
Ïåðåõîä ê ðàâíîñèëüíîìó íåðàâåíñòâó ïðèíÿòî îáîçíà÷àòü çíà-
êîì «⇔».
(2.7.) Äàííîå íåðàâåíñòâî ÿâëÿåòñÿ ñëåäñòâèåì íåêîòîðîãî äðó-
ãîãî íåðàâåíñòâà, åñëè êàæäîå ðåøåíèå äðóãîãî íåðàâåíñòâà ÿâëÿ-
åòñÿ ðåøåíèåì äàííîãî.
Ïðèìåð 1. Ðàâíîñèëüíû ëè íåðàâåíñòâà:
à)
01
2
<+
x
è
01
2
<+−
xx
? á)
1>
x
è
1
2
>x
?
Ðåøåíèå.
à) Äîêàæåì, ÷òî íåðàâåíñòâî
01
2
<+−
xx
íå èìååò ðåøåíèé.
Äåéñòâèòåëüíî,
0
4
3
2
1
4
3
4
1
2
1
21
2
22
>+
−=++⋅−=+−
xxxxx
,
÷òî ïðîòèâîðå÷èò íåðàâåíñòâó
01
2
<+−
xx
. Íåðàâåíñòâî
01
2
<+
x
òàêæå íå èìååò ðåøåíèé.
Îòâåò: äà.
á) Ìîæíî ïðîâåðèòü, ÷òî ñðåäè ðåøåíèé âòîðîãî íåðàâåíñòâà
åñòü ÷èñëî 2, íå ÿâëÿþùååñÿ ðåøåíèåì ïåðâîãî íåðàâåíñòâà.
Îòâåò: íåò.
Ïåðå÷èñëèì îñíîâíûå ñâîéñòâà ðàâíîñèëüíîñòè íåðàâåíñòâ:
Òåîðåìà 1. Åñëè ê îáåèì ÷àñòÿì íåðàâåíñòâà ïðèáàâèòü îäíî è
òî æå âûðàæåíèå, îïðåäåëåííîå íà ÎÄÇ èñõîäíîãî íåðàâåíñòâà,
òî ïîëó÷èì íåðàâåíñòâî, ðàâíîñèëüíîå äàííîìó íåðàâåíñòâó.
Èëè â âèäå ñõåìû:
ÎÄÇ
() () () ()
,
() ()
.
fx px gx px
fx gx
x
+>+
>⇔
∈
 ÷àñòíîñòè, åñëè ïåðåíåñòè ñëàãàåìîå èç îäíîé ÷àñòè íåðàâåí-
ñòâà â äðóãóþ, òî ïîëó÷èòñÿ íåðàâåíñòâî, ðàâíîñèëüíîå èñõîäíî-
ìó íåðàâåíñòâó.
Òðåáîâàíèå x ∈ ÎÄÇ â ôîðìóëèðîâêå òåîðåìû ñóùåñòâåííî.
Åñëè ôóíêöèÿ
)
(
xp
îïðåäåëåíà íå äëÿ âñåõ õ èç ÎÄÇ, òî ðàâíî-
ñèëüíîñòü íàðóøàåòñÿ, è ïðåîáðàçîâàíèå ìîæåò ïðèâåñòè ê ïîòåðå
êîðíåé.
Ëåêöèÿ 2
Ìåòîäû ðåøåíèÿ íåðàâåíñòâ
Íàïîìíèì îïðåäåëåíèå è íåêîòîðûå îñíîâíûå ñâîéñòâà ÷èñëî-
âûõ íåðàâåíñòâ.
(2.1.) ×èñëî À áîëüøå ÷èñëà Â, åñëè ðàçíîñòü À  ïîëî-
æèòåëüíîå ÷èñëî.
(2.2.) ×èñëî À ìåíüøå ÷èñëà Â, åñëè ðàçíîñòü À  îòðè-
öàòåëüíîå ÷èñëî.
Äëÿ ÷èñåë À è  âåðíî îäíî è òîëüêî îäíî óòâåðæäåíèå:
BA >
,
BA
<
èëè
BA
=
, ïðè÷åì ÷èñëî À ðàâíî ÷èñëó  òîãäà è òîëüêî
òîãäà, êîãäà ðàçíîñòü À Â ðàâíà íóëþ.
 âèäå ñõåìû:
.0
,0
,0
=−⇔=
<−⇔<
>−⇔>
BABA
BABA
BABA
Íåêîòîðûå ñâîéñòâà ÷èñëîâûõ íåðàâåíñòâ
Ïðè ðåøåíèè íåðàâåíñòâ íàèáîëåå ÷àñòî ïðèìåíÿþòñÿ ñëåäóþ-
ùèå ñâîéñòâà ÷èñëîâûõ íåðàâåíñòâ.
1) Åñëè
ba
>
, òî
cbca
+>+
.
2) Åñëè
ba
>
è
0>
c
, òî
bcac
>
.
3) Åñëè
ba
>
è
0<
c
, òî
bcac
<
.
4) Åñëè
0>> ba
, à
n
íàòóðàëüíîå ÷èñëî, òî
nn
ba
>
.
5) Åñëè
0>>
ba
, à
n
íàòóðàëüíîå ÷èñëî, òî
nn
ba
>
.
Íåðàâåíñòâà ñ ïåðåìåííîé
Íåðàâåíñòâî ñ îäíîé ïåðåìåííîé èìååò âèä
)()( xgxf ∨
,
ãäå
)
(
xf
,
)
(
xg
íåêîòîðûå ôóíêöèè. Ïðè ýòîì:
(2.3.) Ðåøåíèåì íåðàâåíñòâà íàçûâàþò çíà÷åíèå ïåðåìåííîé,
ïðè ïîäñòàíîâêå êîòîðîãî â äàííîå íåðàâåíñòâî ïîëó÷àåòñÿ âåð-
íîå ÷èñëîâîå íåðàâåíñòâî.
(2.4.) Ðåøèòü íåðàâåíñòâî îçíà÷àåò íàéòè âñå åãî ðåøåíèÿ
èëè äîêàçàòü, ÷òî ðåøåíèé íåò.

28
29
Ìåòîäû ðåøåíèÿ íåðàâåíñòâ
Ëåêöèÿ 2
(2.9.) Ðåøåíèåì ñèñòåìû íåðàâåíñòâ íàçûâàþò òàêîå çíà÷åíèå
ïåðåìåííîé, ïðè êîòîðîì íåðàâåíñòâà ñèñòåìû îáðàùàþòñÿ â âåð-
íûå ÷èñëîâûå íåðàâåíñòâà.
(2.10.) Ðåøèòü ñèñòåìó íåðàâåíñòâ çíà÷èò íàéòè ìíîæåñòâî
çíà÷åíèé ïåðåìåííîé, êàæäîå èç êîòîðûõ îáðàùàåò íåðàâåíñòâà
ñèñòåìû â âåðíûå ÷èñëîâûå íåðàâåíñòâà.
Ïðèìåð 3. Ðåøèòå ñèñòåìó íåðàâåíñòâ
≤
>
>
.102
,164
,7
2
x
x
x
Ðåøåíèå. Èç ïðîñòåéøèõ ñâîéñòâ íåðàâåíñòâ ñëåäóåò, ÷òî âòî-
ðîå íåðàâåíñòâî ñèñòåìû âûïîëíåíî ïðè
4>
x
, à òðåòüå ïðè
5≤
x
. Ïðè
4>x
16
2
>
x
, à ñëåäîâàòåëüíî, è
7
2
>
x
.
Ïîëó÷èì:
2
7,
4,
5
x
x
x
>
>
≤
⇔
7,
45
x
x
>
<≤
⇔
.54 ≤<
x
Îòâåò: (4; 5].
Ïðèìå÷àíèå. Ïðè ðåøåíèè ìû ó÷èòûâàëè, ÷òî íåðàâåíñòâî
7
2
>
x
ðàâíîñèëüíî íåðàâåíñòâó
7
>
x
ïðè õ ïîëîæèòåëüíîì.
(2.11.) Áóäåì ãîâîðèòü, ÷òî çàäàíà ñîâîêóïíîñòü íåðàâåíñòâ ñ
îäíîé ïåðåìåííîé, åñëè òðåáóåòñÿ íàéòè âñå òàêèå çíà÷åíèÿ ïåðå-
ìåííîé, ïðè êàæäîì èç êîòîðûõ õîòÿ áû îäíî èç íåðàâåíñòâ, îáðà-
çóþùèõ ñîâîêóïíîñòü, îáðàùàåòñÿ â âåðíîå ÷èñëîâîå íåðàâåíñòâî.
Ñòàíäàðòíîå îáîçíà÷åíèå:
11
22
() ()
() ().
fx gx
fx g x
>
<
(2.12.) Ðåøåíèåì ñîâîêóïíîñòè íåðàâåíñòâ íàçûâàþò çíà÷åíèå
ïåðåìåííîé, îáðàùàþùåå õîòÿ áû îäíî èç íåðàâåíñòâ, îáðàçóþ-
ùèõ ñîâîêóïíîñòü, â âåðíîå ÷èñëîâîå íåðàâåíñòâî.
(2.13.) Ðåøèòü ñîâîêóïíîñòü íåðàâåíñòâ îçíà÷àåò íàéòè âñå
ðåøåíèÿ èëè äîêàçàòü, ÷òî ñîâîêóïíîñòü ðåøåíèé íå èìååò.
Ïðèìåð 4. Ðåøèòå ñîâîêóïíîñòü íåðàâåíñòâ
2
7
416
2 10.
x
x
x
>
>
≤
Òåîðåìà 2. Åñëè îáå ÷àñòè íåðàâåíñòâà óìíîæèòü èëè ðàçäå-
ëèòü íà îäíî è òî æå âûðàæåíèå, áîëüøåå íóëÿ, îïðåäåëåííîå íà
ÎÄÇ èñõîäíîãî íåðàâåíñòâà, òî ïîëó÷èòñÿ íåðàâåíñòâî, ðàâíîñèëü-
íîå èñõîäíîìó íåðàâåíñòâó.
Èëè â âèäå ñõåìû:
ÎÄÇ
() (), () () () (),
() 0 .
fx gx fx px gx px
px x
>⋅>⋅
⇔
>∈
 ÷àñòíîñòè, åñëè îáå ÷àñòè íåðàâåíñòâà óìíîæèòü èëè ðàçäå-
ëèòü íà îäíî è òî æå ïîëîæèòåëüíîå ÷èñëî, òî ïîëó÷èòñÿ íåðàâåí-
ñòâî, ðàâíîñèëüíîå èñõîäíîìó íåðàâåíñòâó.
Òåîðåìà 3. Åñëè îáå ÷àñòè íåðàâåíñòâà óìíîæèòü èëè ðàçäå-
ëèòü íà îäíî è òî æå âûðàæåíèå, ìåíüøåå íóëÿ, îïðåäåëåííîå íà
ÎÄÇ èñõîäíîãî íåðàâåíñòâà, à çàòåì ïîìåíÿòü çíàê íåðàâåíñòâà
íà ïðîòèâîïîëîæíûé, òî ïîëó÷èòñÿ íåðàâåíñòâî, ðàâíîñèëüíîå
èñõîäíîìó íåðàâåíñòâó.
Èëè â âèäå ñõåìû:
ÎÄÇ
() ()
,
() () () ()
,
()
0.
fx gx fx px gx px
px x
>⋅<⋅
⇔
<∈
 ÷àñòíîñòè, åñëè îáå ÷àñòè íåðàâåíñòâà óìíîæèòü èëè ðàçäå-
ëèòü íà îäíî è òî æå îòðèöàòåëüíîå ÷èñëî, à çàòåì ïîìåíÿòü çíàê
íåðàâåíñòâà íà ïðîòèâîïîëîæíûé, òî ïîëó÷èòñÿ íåðàâåíñòâî, ðàâ-
íîñèëüíîå èñõîäíîìó íåðàâåíñòâó.
Íåêîòîðûå íåðàâåíñòâà óäàåòñÿ ïóòåì ïðåîáðàçîâàíèé ñâåñòè ê
ëèíåéíûì íåðàâåíñòâàì. Ðàññìîòðèì íåñêîëüêî ïðèìåðîâ.
Ïðèìåð 2. Ðåøèòå íåðàâåíñòâî
22
)
4
(
)
6
(
−>−
xx
.
Ðåøåíèå. Ïðåîáðàçóåì èñõîäíîå íåðàâåíñòâî. Ïîëó÷èì:
0
)
4
(
)
6
(
22
>−−−
xx
⇔
0
)
168
(
)
3612
(
22
>+−−+−
xxxx
⇔
⇔
0204 >+−
x
⇔
204 <
x
⇔
5<
x
.
Îòâåò: (∞; 5).
(2.8.) Áóäåì ãîâîðèòü, ÷òî çàäàíà ñèñòåìà íåðàâåíñòâ ñ îäíîé
ïåðåìåííîé, åñëè òðåáóåòñÿ íàéòè âñå òàêèå çíà÷åíèÿ ïåðåìåí-
íîé, ïðè êîòîðûõ íåðàâåíñòâà ñèñòåìû îáðàùàþòñÿ â âåðíûå ÷èñ-
ëîâûå íåðàâåíñòâà.
Ñòàíäàðòíîå îáîçíà÷åíèå:
≤
>
)
.
(
)
(
)
,
(
)
(
22
11
xgxf
xgxf

30
31
Ìåòîäû ðåøåíèÿ íåðàâåíñòâ
Ëåêöèÿ 2
Èç äîêàçàííûõ óòâåðæäåíèé òàêæå ñëåäóåò, ÷òî ïðè óñëîâèè
0≠
a
,
0<
D
íåðàâåíñòâî
0
)
(
>
xaf
âûïîëíåíî ïðè âñåõ äåéñòâè-
òåëüíûõ õ. Èíà÷å ãîâîðÿ, åñëè äèñêðèìèíàíò êâàäðàòíîãî òðåõ-
÷ëåíà îòðèöàòåëåí, òî ïðè âñåõ çíà÷åíèÿõ àðãóìåíòà çíàê êâàä-
ðàòíîãî òðåõ÷ëåíà ñîâïàäàåò ñî çíàêîì åãî ñòàðøåãî êîýôôèöè-
åíòà.
Äëÿ äîêàçàòåëüñòâà ñëåäóþùèõ òåîðåì äîñòàòî÷íî ðàçëîæèòü
êâàäðàòíûé òðåõ÷ëåí íà ìíîæèòåëè:
)
)(
(
21
2
xxxxacbxax
−−=++
.
Òåîðåìà 6. Åñëè
0<
a
è
0>
D
, òî äëÿ âñåõ äåéñòâèòåëüíûõ
)
;
(
21
xxx
∈
âûïîëíåíî íåðàâåíñòâî
0
)
(
>
xf
, à äëÿ âñåõ
1
(;)
xx
∈−∞ ∪
2
(; )
x
∪+∞
âûïîëíåíî íåðàâåíñòâî
0)( <xf
.
Òåîðåìà 7. Åñëè
0>
a
è
0>
D
, òî äëÿ âñåõ äåéñòâèòåëüíûõ
)
;
(
21
xxx
∈
âûïîëíåíî íåðàâåíñòâî
0)( <xf
, à äëÿ âñåõ
1
(;)
xx
∈−∞ ∪
2
(; )
x
∪+∞
âûïîëíåíî íåðàâåíñòâî
0
)
(
>
xf
.
Ïóñòü, íàïðèìåð,
0>
a
,
0>
D
; åñëè
)
;
(
21
xxx
∈
, òî
0
1
>−
xx
,
à
0
2
<−
xx
, îòêóäà
0
)
)(
(
)
(
21
<−−=
xxxxaxf
, ÷òî è òðåáîâàëîñü
äîêàçàòü.
Ñëåäóþùèå óòâåðæäåíèÿ ìîæíî äîêàçàòü, åñëè âîñïîëüçîâàòü-
ñÿ ðàçëîæåíèåì:
2
1
2
)(
xxacbxax
−=++
.
Òåîðåìà 8. Åñëè
0<
a
è
0=
D
, òî äëÿ âñåõ
a
b
x
2
−≠
âûïîëíå-
íî íåðàâåíñòâî
0
)
(
<
xf
.
Òåîðåìà 9. Åñëè
0>
a
è
0=
D
, òî äëÿ âñåõ
a
b
x
2
−≠
âûïîëíå-
íî íåðàâåíñòâî
0
)
(
>
xf
.
Ñäåëàéòå ýòî ñàìîñòîÿòåëüíî.
Ðåøåíèÿ êâàäðàòè÷íîãî íåðàâåíñòâà ìîãóò áûòü ïîëó÷åíû èç
ãðàôèêà êâàäðàòè÷íîé ôóíêöèè ïàðàáîëû.
Ïðèìåð 5. Ðåøèòå íåðàâåíñòâî
082
2
<+−−
xx
.
Ðåøåíèå. Ñòðîèì ñõåìàòè÷åñêè ãðàôèê ôóíêöèè f(x) (ðèñ. 1).
Ðåøåíèå. Êàê óêàçûâàëîñü ðàíåå, âòîðîå íåðàâåíñòâî ñèñòåìû
âûïîëíåíî ïðè
4>x
, à òðåòüå íåðàâåíñòâî ïðè
5≤
x
.
Îáúåäèíåíèå ìíîæåñòâ ðåøåíèé ýòèõ íåðàâåíñòâ âñÿ ÷èñëî-
âàÿ îñü.
Îòâåò: (∞; +∞).
Ïðèìåíÿþò è áîëåå ñëîæíûå êîíñòðóêöèè.
Íàïðèìåð, ñìåøàííûå ñèñòåìû óðàâíåíèé è íåðàâåíñòâ, ñî-
âîêóïíîñòè ñèñòåì è òàê äàëåå. Ðåøàÿ íåðàâåíñòâà, ìû â õîäå
ïðåîáðàçîâàíèé áóäåì ïîëó÷àòü íå òîëüêî íåðàâåíñòâà, íî è
óðàâíåíèÿ, à òàêæå ñèñòåìû (ñîâîêóïíîñòè) óðàâíåíèé è íå-
ðàâåíñòâ.
Êâàäðàòè÷íûå íåðàâåíñòâà
Êâàäðàòè÷íûì íåðàâåíñòâîì (íåðàâåíñòâîì âòîðîé ñòåïåíè)
áóäåì íàçûâàòü íåðàâåíñòâî âèäà
0
)
(
∨
xf
, ãäå
cbxaxxf
++=
2
)(
,
è
0≠
a
. Ïðèìå÷àíèå. Çíàê
∨
ïîäðàçóìåâàåò îäèí èç çíàêîâ:
>
,
<
,
≥
èëè
≤
.
Ïóñòü
acbD
4
2
−=
, à
1
x
è
2
x
êîðíè
)
(
xf
(åñëè êîðíè ñóùå-
ñòâóþò), ïðè÷åì
21
xx
<
.
Âåðíû ñëåäóþùèå òåîðåìû.
Òåîðåìà 4. Åñëè
0<
a
è
0<
D
, òî äëÿ âñåõ õ âûïîëíåíî íåðà-
âåíñòâî
0)( <xf
.
Òåîðåìà 5. Åñëè
0>
a
è
0<
D
, òî äëÿ âñåõ õ âûïîëíåíî íåðà-
âåíñòâî
0
)
(
>
xf
.
Äåéñòâèòåëüíî,
−
+
+=−
+=++=
2
22
2
4
242
)(
a
D
a
b
xa
a
D
a
b
xacbxaxxf
.
Òàêèì îáðàçîì, åñëè
0<
D
, òî
0
4
2
2
2
>
−
+
+
a
D
a
b
x
, è çíàê
)(xf
ñîâïàäàåò ñî çíàêîì ñòàðøåãî êîýôôèöèåíòà à.
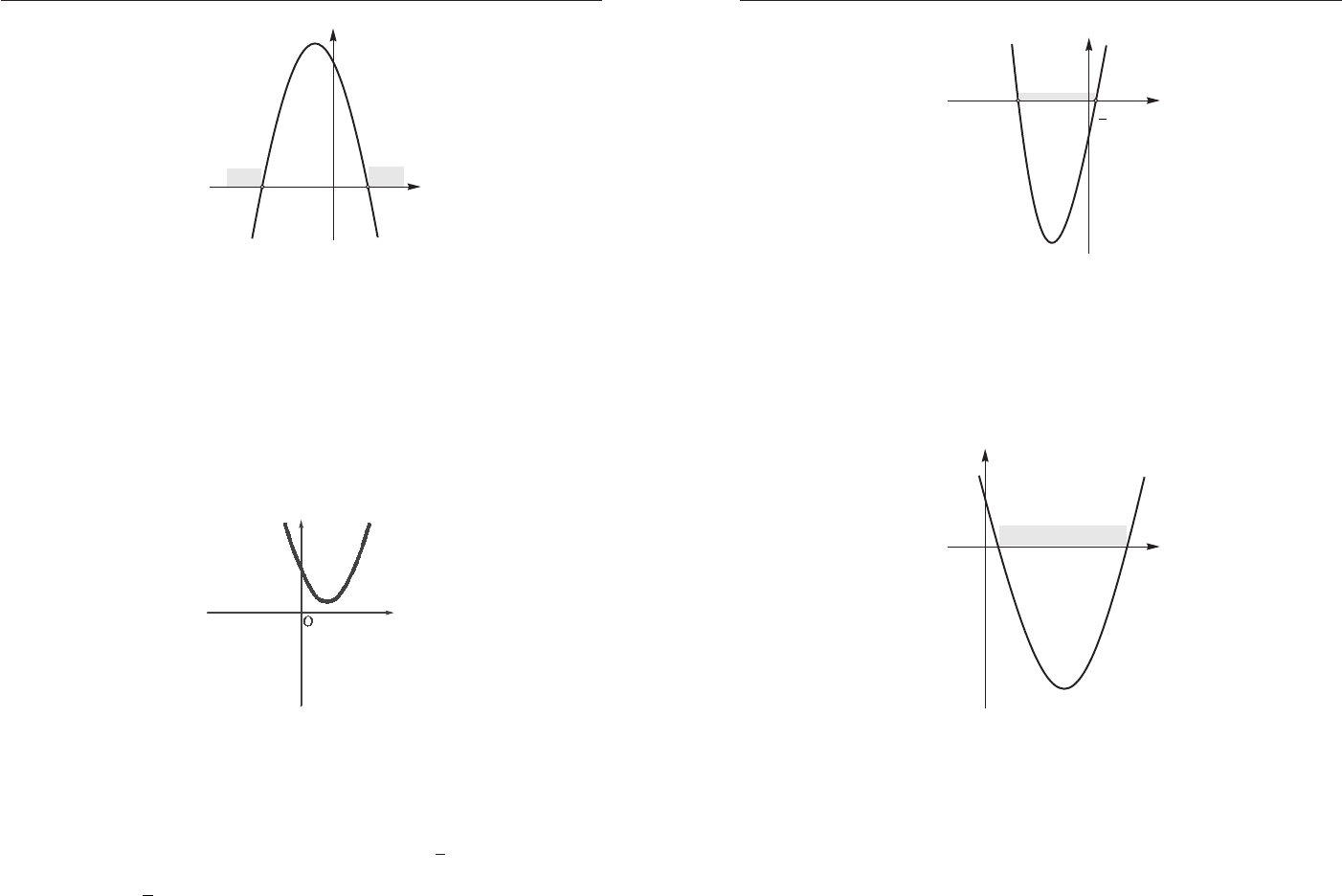
32
33
Ìåòîäû ðåøåíèÿ íåðàâåíñòâ
Ëåêöèÿ 2
x
y
–5
2
3
Ðèñ. 3
Ïðèìåð 8. Ðåøèòå íåðàâåíñòâî
45
2
−≤−
xx
.
Ðåøåíèå. Ïåðåïèøåì íåðàâåíñòâî â âèäå
045
2
≤+−
xx
.
1)
0)( =xf
ïðè
1
1
=
x
è
4
2
=
x
;
2) èç ðèñóíêà âèäíî, ÷òî
≤
()
0
fx
ïðè
41 ≤≤ x
(ðèñ. 4).
x
y
14
Ðèñ. 4
Èíîãäà ñâîéñòâàìè êâàäðàòè÷íûõ íåðàâåíñòâ óäàåòñÿ âîñïîëü-
çîâàòüñÿ ïðè ðåøåíèè áîëåå ñëîæíûõ íåðàâåíñòâ.
Ïðèìåð 9. Ðåøèòå íåðàâåíñòâî
)
95
(
7
)
1
)(
95
(
22
++≤−++
xxxxx
.
Ðåøåíèå. Ðàçäåëèì îáå ÷àñòè íåðàâåíñòâà íà âûðàæåíèå
095
2
>++
xx
. Ïîëó÷èì ðàâíîñèëüíîå íåðàâåíñòâî:
71 <−
x
.
Îòâåò: (∞; 8).
x
y
–4 2
Ðèñ. 1
Èç ðèñóíêà âèäíî, ÷òî
0
)
(
<
xf
ïðè
∈−∞− ∪ +∞
(
;4
)(
2;
)
x
.
Îòâåò:
(
;4
)(
2;
)
−∞ − ∪ + ∞ .
Ïðèìåð 6. Ðåøèòå íåðàâåíñòâî
013
2
<+−
xx
.
Ðåøåíèå. Ñòðîèì ñõåìàòè÷åñêè ãðàôèê ôóíêöèè (ðèñ. 2)
013
2
>+−=
xxy
.
Òàê êàê
0>
a
è
0<
D
, òî äëÿ âñåõ äåéñòâèòåëüíûõ çíà÷åíèé õ
âûïîëíåíî íåðàâåíñòâî
0)( >xf
.
Îòâåò: íåò ðåøåíèé.
N
O
Ðèñ. 2
Ïðèìåð 7. Ðåøèòå íåðàâåíñòâî
010133
2
<−+
xx
.
Ðåøåíèå. Ñòðîèì ñõåìàòè÷åñêè ãðàôèê ôóíêöèè (ðèñ. 3)
10133
2
−+=
xxy
.
Èç ðèñóíêà âèäíî, ÷òî
0
)
(
<
xf
ïðè
)
;5
(
3
2
−∈
x
.
Îòâåò:
2
(5; )
3
−
.
34
35
Ìåòîäû ðåøåíèÿ íåðàâåíñòâ
Ëåêöèÿ 2
Ïðèìåð 10. Ðåøèòå íåðàâåíñòâî
0
)
4
)(
2
)(
1
(
<−−−
xxx
.
Ðåøåíèå. Îòìåòèì íà ÷èñëîâîé îñè êîðíè êàæäîãî èç ëèíåé-
íûõ ìíîæèòåëåé (ðèñ 6):
N
+
−
+
−
"
Ðèñ. 6
Âûÿñíèì çíàêè ëåâîé ÷àñòè íåðàâåíñòâà íà êàæäîì èç ïðîìå-
æóòêîâ: (4; +∞), (2; 4), (1; 2), (∞; 1). Ðåçóëüòàòû èññëåäîâàíèÿ
ïðåäñòàâèì â òàáëèöå.
(4; +∞)
(2; 4)
(1; 2)
(∞; 1)
)
4
(
−
x
+
)
2
(
−
x
+
+
)
1
(
−
x
+
+
+
)
(
xP
+
+
Íà ïðîìåæóòêå (4; +∞) âñå ìíîæèòåëè ëåâîé ÷àñòè íåðàâåíñòâà
ïîëîæèòåëüíû, à ïîòîìó è âñå ïðîèçâåäåíèå áóäåò ïîëîæèòåëüíî.
Íà ïðîìåæóòêå (2; 4) îäèí ìíîæèòåëü
)4( −x
ìåíÿåò çíàê, à
âñå îñòàëüíûå îñòàþòñÿ ïîëîæèòåëüíûìè, à ïîòîìó ïðîèçâåäåíèå
áóäåò îòðèöàòåëüíûì (ñìåíèò çíàê).
Íà ïðîìåæóòêå (1; 2) óæå äâà ìíîæèòåëÿ
)4( −x
è
)2( −x
ñòàíóò
îòðèöàòåëüíûìè, à ìíîæèòåëü
)
1
(
−
x
îñòàíåòñÿ ïîëîæèòåëüíûì,
à ïîòîìó âñå ïðîèçâåäåíèå áóäåò ïîëîæèòåëüíî (âíîâü ñìåíèò çíàê).
È íàêîíåö, íà ïðîìåæóòêå (∞; 1) óæå âñå òðè ìíîæèòåëÿ ñòà-
íóò îòðèöàòåëüíûìè, ïðîèçâåäåíèå ñìåíèò çíàê ïîñëåäíèé ðàç
(ñòàíåò îòðèöàòåëüíûì).
Îòâåò:
(;1)(2;4)
−∞ ∪
.
Êðàòêèé êîììåíòàðèé:
1) Íå ïðèíÿòî (íî íå áóäåò îøèáêîé), åñëè ìíîæåñòâî ðåøåíèé
äàííîãî íåðàâåíñòâà çàïèñàíî â âèäå
42 <<
x
,
1<x
.
2) Îòìåòèì, ÷òî ïðè âûïîëíåíèè ðèñóíêà ìàñøòàá íà êîîðäè-
íàòíîé îñè ñîáëþäàòü íåîáÿçàòåëüíî, ïîñêîëüêó âàæåí ïîðÿäîê
ðàñïîëîæåíèÿ êîðíåé, à íå ðàññòîÿíèÿ ìåæäó íèìè. Áîëåå òîãî,
åñëè, íàïðèìåð, äâà êîðíÿ ðàñïîëîæåíû íà îñè ñîâñåì áëèçêî
äðóã ê äðóãó, íî äàëåêî îò òðåòüåãî êîðíÿ, íåâîçìîæíî ïîñòðîèòü
÷åðòåæ, âñå ðàññòîÿíèÿ íà êîòîðîì ïðîïîðöèîíàëüíû èñòèííûì
ðàññòîÿíèÿì.
Ìåòîä èíòåðâàëîâ äëÿ ðàöèîíàëüíûõ íåðàâåíñòâ
Ðàöèîíàëüíûìè íàçûâàþò íåðàâåíñòâà, ñîäåðæàùèå òîëüêî
öåëûå ðàöèîíàëüíûå è äðîáíî-ðàöèîíàëüíûå ôóíêöèè.
Öåëîå ðàöèîíàëüíîå íåðàâåíñòâî ìîæíî ïðèâåñòè ê âèäó
0
)
(
∨
xP
, à äðîáíî-ðàöèîíàëüíîå ê âèäó
0
)
(
)
(
∨
xQ
xP
, ãäå
)(xP
,
)
(
xQ
ïðèâåäåííûå ìíîãî÷ëåíû.
Ðàöèîíàëüíûå íåðàâåíñòâà ìîæíî ðåøàòü ìåòîäîì èíòåðâà-
ëîâ, îñíîâûâàÿñü íà ïðîñòîì íàáëþäåíèè: çíàê ïðîèçâåäåíèÿ
(÷àñòíîãî) çàâèñèò òîëüêî îò çíàêîâ êàæäîãî èç ìíîæèòåëåé
(äåëèìîãî è äåëèòåëåé).
Ïðèìåíèì ìåòîä èíòåðâàëîâ ê íåðàâåíñòâó âèäà
0
)
(
)
)(
(
21
∨−−−
n
xxxxxx
K
,
ïðè÷åì áóäåì ñ÷èòàòü, ÷òî
n
xxx
<<<
K
21
.
1) Îòìåòèì íà ÷èñëîâîé îñè êîðíè ëåâîé ÷àñòè íåðàâåíñòâà, òî
åñòü ÷èñëà
1
x
,
2
x
, ...,
n
x
(ðèñ.5).
N
N
N
N
!
N
n
Ðèñ. 5
2) Âûÿñíèì çíàêè ëåâîé ÷àñòè íåðàâåíñòâà íà êàæäîì èç ïðî-
ìåæóòêîâ (x
n
; +∞),
)
;
(
1
nn
xx
−
,
)
;
(
12
−−
nn
xx
, ...,
)
;
(
32
xx
,
)
;
(
21
xx
,
)
;
(
1
x
−∞
.
Ðàññìîòðèì ñëó÷àè:
Íà ïðîìåæóòêå (x
n
; +∞) âñå ìíîæèòåëè ëåâîé ÷àñòè íåðà-
âåíñòâà ïîëîæèòåëüíûå, à ïîòîìó è âñå ïðîèçâåäåíèå áóäåò ïîëî-
æèòåëüíî.
Íà ïðîìåæóòêå
)
;
(
1
nn
xx
−
îäèí ìíîæèòåëü (õõ
n
) îòðèöà-
òåëüíûé, à âñå îñòàëüíûå ïîëîæèòåëüíûå, à ïîòîìó âñå ïðîèçâå-
äåíèå áóäåò îòðèöàòåëüíî (ñìåíèò çíàê).
Íà ïðîìåæóòêå
)
;
(
12
−−
nn
xx
óæå äâà ìíîæèòåëÿ îòðèöàòåëü-
íûå, à âñå îñòàëüíûå ïîëîæèòåëüíûå, à ïîòîìó âñå ïðîèçâåäåíèå ïîëî-
æèòåëüíî (âíîâü ñìåíèò çíàê). È òàê äàëåå.
È íàêîíåö, íà ïðîìåæóòêå
)
;
(
1
x
−∞
óæå âñå ìíîæèòåëè îòðèöà-
òåëüíûå, è ïðîèçâåäåíèå ñìåíèò çíàê ïîñëåäíèé ðàç è ñòàíåò ïîëî-
æèòåëüíûì èëè îòðèöàòåëüíûì, â çàâèñèìîñòè îò ÷èñëà ñìåí çíàêà.
Îòâåò ìîæíî ïðîñòî «ñ÷èòàòü ñ ðèñóíêà».
+
...
36
37
Ìåòîäû ðåøåíèÿ íåðàâåíñòâ
Ëåêöèÿ 2
Ïðè ðåøåíèè äðîáíûõ íåðàâåíñòâ (íåðàâåíñòâ âèäà
0
)
(
)
(
∨
xQ
xP
)
ìîæíî ïîñòóïàòü àíàëîãè÷íî:
1) íàéòè êîðíè ÷èñëèòåëÿ è çíàìåíàòåëÿ, à çàòåì ðàçëîæèòü
ìíîãî÷ëåíû
)
(
xP
è
)
(
xQ
íà ìíîæèòåëè;
2) çàìåíèòü êâàäðàòè÷íûå ìíîæèòåëè íà 1 èëè 1 (â çàâèñè-
ìîñòè îò çíàêà);
3) îòìåòèòü íà ÷èñëîâîé îñè êîðíè ÷èñëèòåëÿ è çíàìåíàòåëÿ;
4) îïðåäåëèòü çíàê äðîáè â êàæäîì èç èíòåðâàëîâ, íà êîòîðûå
êîðíè ÷èñëèòåëÿ è çíàìåíàòåëÿ ðàçáèâàþò ÷èñëîâóþ îñü.
Ïðèìåð 12. Ðåøèòå íåðàâåíñòâî
.0
3
)
2
)(
1
(
≤
−
−−
x
xx
Ðåøåíèå. Îòìåòèì íà ÷èñëîâîé îñè êîðíè ÷èñëèòåëÿ è çíàìå-
íàòåëÿ (ðèñ. 8):
N
+
+
−−
12
3
Ðèñ. 8
Ïðè
3>
x
, âûïîëíåíû íåðàâåíñòâà
03 <−
x
,
01 >−
x
,
02 >−
x
,
ïîýòîìó äðîáü îòðèöàòåëüíà.  êàæäîì èç êîðíåé ÷èñëèòåëÿ è çíà-
ìåíàòåëÿ äðîáü ìåíÿåò ñâîé çíàê. Íåðàâåíñòâî íåñòðîãîå, ïîýòîìó
÷èñëà 1 è 2 ðåøåíèÿ íåðàâåíñòâà.
Îòâåò:
[
1; 2
](
3;
)
x
∈∪+∞
.
Ïðèìåð 13. Ðåøèòå íåðàâåíñòâî
.0
)
1
(
)
6
)(
4
)(
1
(
22
22
≥
−
−−−−
xx
xxxx
Çàïèøåì ðàçëîæåíèå ëåâîé ÷àñòè íåðàâåíñòâà íà ëèíåéíûå
ìíîæèòåëè:
.0
)
1
)(
1
(
)
3
(
)
2
)(
2
)(
1
(
2
2
≥
+−
−+−−
xxx
xxxx
Ðàññòàâèì íà îñè êîðíè ëåâîé ÷àñòè íåðàâåíñòâà (ðèñ. 9):
Ðèñ. 9
Îáðàòèì âíèìàíèå, ÷òî â òî÷êàõ
;2−
0 è 1 ëåâàÿ ÷àñòü íåðà-
âåíñòâà çíàêà íå ìåíÿåò, à â òî÷êàõ 1, 2 è 3 çíàê ìåíÿåò.
Íåìíîãî óñëîæíèì ñèòóàöèþ. Ïóñòü
)
(
xP
ïðîèçâîëüíûé ìíî-
ãî÷ëåí, è ðàññìîòðèì íåðàâåíñòâî
0
)
(
∨
xP
.
Êàê èçâåñòíî,
)(xP
ìîæíî ïðåäñòàâèòü â âèäå ïðîèçâåäåíèÿ
íåñêîëüêèõ ëèíåéíûõ è êâàäðàòè÷íûõ ìíîæèòåëåé, êîòîðûå óæå
íå ðàçëàãàþòñÿ íà ëèíåéíûå ìíîæèòåëè (âñåãäà ïîëîæèòåëüíû):
11
22
111
()()( )( )
0
n k
nkk
xx xx x pxq x pxq
αβ
αβ
−−++ ++∨
KK
.
Ïîñëåäíåå íåðàâåíñòâî ìîæíî ïðèâåñòè ê âèäó
0
)
(
)
(
1
1
∨−−
αα
n
n
xxxx
K
.
Ïóñòü äëÿ îïðåäåëåííîñòè
n
xxx
<<<
K
21
. Îòìåòèì íà ÷èñëî-
âîé îñè âñå êîðíè ëåâîé ÷àñòè íåðàâåíñòâà, òî åñòü:
1
x
,
2
x
, ...,
n
x
.
Âûÿñíèì çíàêè ëåâîé ÷àñòè íåðàâåíñòâà íà êàæäîì èç ïðîìåæóòêîâ:
)
;
(
1
x
−∞
,
)
;
(
21
xx
,
)
;
(
32
xx
, ...,
)
;
(
12
−−
nn
xx
,
)
;
(
1
nn
xx
−
,
(
;
)
n
x
+∞
.
Íà êàæäîì èç èíòåðâàëîâ êàæäûé èç ìíîæèòåëåé ñîõðàíÿåò ïî-
ñòîÿííûé çíàê.
Òåì ñàìûì, çíàê ïðîèçâåäåíèÿ íà êàæäîì èç èíòåðâàëîâ îï-
ðåäåëÿåòñÿ îäíîçíà÷íî ïî ÷èñëó îòðèöàòåëüíûõ ìíîæèòåëåé. Íå-
ðàâåíñòâî
0
)
(
>
xP
âûïîëíÿåòñÿ â òåõ èíòåðâàëàõ, â êîòîðûõ ÷èñ-
ëî îòðèöàòåëüíûõ ìíîæèòåëåé ÷åòíî.
 îñòàëüíûõ èíòåðâàëàõ èìååò ìåñòî íåðàâåíñòâî
0
)
(
<
xP
.
Ïðèìåð 11. Ðåøèòå íåðàâåíñòâî
.0
)
3
(
)
2
(
)
1
(
22
≤−−−
xxx
Ðåøåíèå. Îòìåòèì íà ÷èñëîâîé îñè êîðíè ëåâîé ÷àñòè íåðàâåíñòâà
(ðèñ. 7) è îïðåäåëèì çíàêè ëåâîé ÷àñòè íåðàâåíñòâà â êàæäîì èç èí-
òåðâàëîâ.
Ïðè
3>
x
, âûïîëíåíû íåðàâåíñòâà
03 <−
x
,
()
01
2
>−
x
,
()
02
2
>−
x
,
ïîýòîìó çíà÷åíèå âûðàæåíèÿ îòðèöàòåëüíî.  òî÷êå 3 âûðàæåíèå
x
−3
ìåíÿåò çíàê, ñëåäîâàòåëüíî, è âñå âûðàæåíèå ìåíÿåò çíàê, òî
åñòü ïðèíèìàåò ïîëîæèòåëüíûå çíà÷åíèÿ íà èíòåðâàëå
32 <<
x
.
 òî÷êàõ 1 è 2 âûðàæåíèå íå ìåíÿåò çíàê, òî åñòü ñîõðàíÿåò â
ñîîòâåòñòâóþùèõ èíòåðâàëàõ ïîëîæèòåëüíûå çíà÷åíèÿ.
N
++
+
−
12
3
ðèñ. 7
Íåðàâåíñòâî íåñòðîãîå, ïîýòîìó ÷èñëà 1 è 2 ðåøåíèÿ.
Îòâåò:
{}
1; 2
[
3;
)
x
∈∪+∞
.
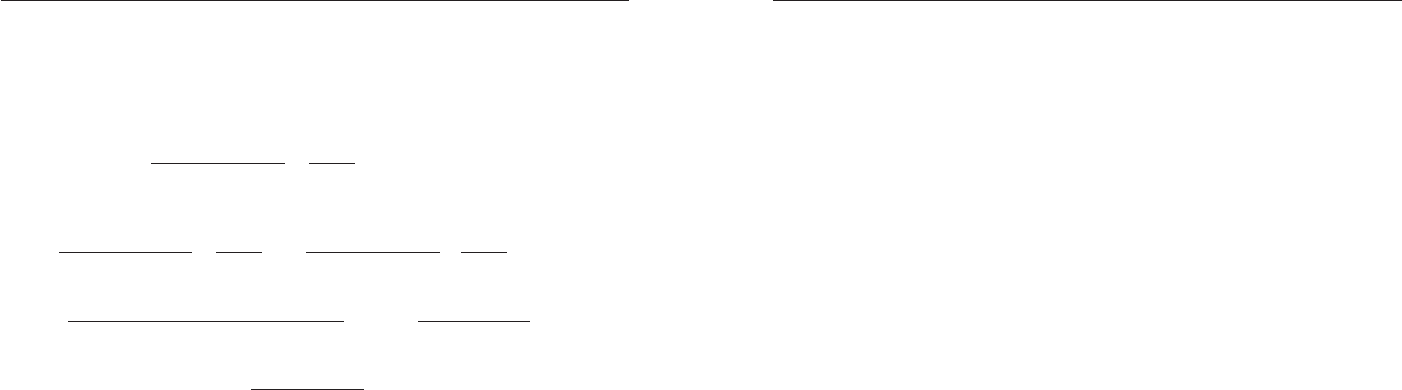
38
39
Ìåòîäû ðåøåíèÿ íåðàâåíñòâ
Ëåêöèÿ 2
Ìåòîä èíòåðâàëîâ
êàê ñëåäñòâèå ñâîéñòâ íåïðåðûâíîñòè
Ìåòîä èíòåðâàëîâ äëÿ íåïðåðûâíûõ ôóíêöèé ìîæåò áûòü îñ-
íîâàí íà ñëåäóþùåì óòâåðæäåíèè.
Òåîðåìà 10. Íåïðåðûâíàÿ ôóíêöèÿ, íå îáðàùàþùàÿñÿ â íóëü
íà íåêîòîðîì èíòåðâàëå, ñîõðàíÿåò íà ýòîì èíòåðâàëå ïîñòîÿí-
íûé çíàê.
Äàííîå óòâåðæäåíèå ìîæíî äîêàçàòü, îïèðàÿñü íà ñëåäóþùåå
óòâåðæäåíèå, ñìûñë êîòîðîãî (íî íå äîêàçàòåëüñòâî) ëåãêî óâè-
äåòü èç ðèñóíêà, à äîêàçàòåëüñòâî ïðèâîäèòñÿ â êóðñå ìàòåìàòè-
÷åñêîãî àíàëèçà.
Òåîðåìà 11 (ÁîëüöàíîÊîøè). Åñëè ôóíêöèÿ
f
íåïðåðûâíà
íà îòðåçêå
]
;
[
ba
è ÷èñëà
)
(
af
è
)
(
bf
ðàçíûõ çíàêîâ, òî íà îòðåçêå
];[ ba
íàéäåòñÿ òàêîå ÷èñëî ñ, ÷òî
0
)
(
=
cf
.
Äîêàçàòåëüñòâî òåîðåìû 10 ïðîâåäåì ìåòîäîì îò ïðîòèâíîãî.
Ïðåäïîëîæèì, ÷òî ñóùåñòâóþò ÷èñëà c è d èç èíòåðâàëà
)
;
(
ba
òàêèå, ÷òî
dc
<
,
0
)
(
>
cf
,
0
)
(
<
df
. Òîãäà ñîãëàñíî òåîðåìå Áîëü-
öàíîÊîøè, ñóùåñòâóåò òàêîå ÷èñëî
p
, ÷òî
dpc
<<
è
0
)
(
=
pf
.
Ïðîòèâîðå÷èå.
Òàêèì îáðàçîì, åñëè ôóíêöèÿ
)
(
xf
íåïðåðûâíà íà íåêîòîðîì
èíòåðâàëå
)
;
(
ba
, òî çíàê ôóíêöèè
)
(
xf
íà ýòîì èíòåðâàëå ìîæíî
âûÿñíèòü ñëåäóþùèì îáðàçîì:
1) Íàéäåì
1
x
,
2
x
, …,
n
x
êîðíè óðàâíåíèÿ
0
)
(
=
xf
. Èíòåð-
âàë
)
;
(
ba
ðàçáèâàåòñÿ íà èíòåðâàëû
)
;
(
1
xa
,
)
;
(
21
xx
, …,
)
;
(
bx
n
,
íà êàæäîì èç êîòîðûõ ôóíêöèÿ
f
ñîõðàíÿåò ïîñòîÿííûé çíàê.
2) Òåïåðü äîñòàòî÷íî âû÷èñëèòü çíà÷åíèå ôóíêöèè â îäíîé òî÷êå
äëÿ êàæäîãî òàêîãî èíòåðâàëà.
Òàêèì îáðàçîì, äëÿ ðåøåíèÿ íåðàâåíñòâà âèäà
0)( ∨xf
ìîæíî
ïîñòóïèòü ñëåäóþùèì îáðàçîì:
1) âûÿñíèòü ïðîìåæóòêè íåïðåðûâíîñòè ôóíêöèè
)
(
xf
;
2) ðåøèòü óðàâíåíèå
0
)
(
=
xf
íà êàæäîì òàêîì ïðîìåæóòêå;
êîðíè óðàâíåíèÿ âìåñòå ñ ãðàíè÷íûìè òî÷êàìè ïðîìåæóòêîâ íå-
ïðåðûâíîñòè ðàçáèâàþò îáëàñòü îïðåäåëåíèÿ íà èíòåðâàëû, íà
êàæäîì èç êîòîðûõ ôóíêöèÿ ñîõðàíÿåò çíàê;
3) âû÷èñëèòü ïî îäíîìó çíà÷åíèþ ôóíêöèè
)(xf
äëÿ êàæäîãî
òàêîãî èíòåðâàëà;
4) çàïèñàòü îòâåò.
Íåðàâåíñòâî íåñòðîãîå, ïîýòîìó êîðíè ñîîòâåòñòâóþùåãî óðàâ-
íåíèÿ (
2±
è 3) âõîäÿò â ìíîæåñòâî ðåøåíèé íåðàâåíñòâà.
Îòâåò:
{}
2
(
1; 0
)(
0;1
)(
1; 2
][
3;
)
−∪−∪∪∪+∞
.
Ïåðåä òåì, êàê ïðèìåíèòü ìåòîä èíòåðâàëîâ, èíîãäà ïðèõî-
äèòñÿ ïðåîáðàçîâûâàòü èñõîäíîå íåðàâåíñòâî.
Ïðèìåð 14.
1
4
56
36172
2
2
+
+
≥
++
++
x
x
xx
xx
.
Ðåøåíèå. Ïðåîáðàçóåì èñõîäíîå íåðàâåíñòâî:
1
4
56
36172
2
2
+
+
≥
++
++
x
x
xx
xx
⇔
0
1
4
)
5
)(
1
(
36172
2
≥
+
+
−
++
++
x
x
xx
xx
⇔
⇔
0
)
5
)(
1
(
)
209
(
36172
22
≥
++
++−++
xx
xxxx
⇔
0
)
5
)(
1
(
168
2
≥
++
++
xx
xx
⇔
⇔
0
)
5
)(
1
(
)
4
(
2
≥
++
+
xx
x
.
Ïðèìåíèì ìåòîä èíòåðâàëîâ.
Îòâåò:
(
;5
){
4
}(
1;
)
−∞ − ∪ − ∪ − +∞
.
Íåðåäêî ïðè ðåøåíèè íåðàâåíñòâ ïðèìåíÿåòñÿ ìåòîä çàìåíû
ïåðåìåííûõ.
Ïðèìåð 15.
180
)
209
)(
23
(
22
<+−+−
xxxx
.
Ðåøåíèå. Ïðåîáðàçóåì èñõîäíîå íåðàâåíñòâî.
Ðàçëîæèì îáà êâàäðàòíûõ òðåõ÷ëåíà íà ìíîæèòåëè. Ïåðåìíî-
æèì ïîëó÷åííûå ìíîæèòåëè. Ïîëó÷èì:
180
)
5
)(
4
)(
2
)(
1
(
<−−−−
xxxx
⇔
180
)
86
)(
56
(
22
<+−+−
xxxx
.
Îáîçíà÷èì
56
2
+−=
xxa
. Òîãäà
180
)
3
(
<+
aa
⇔
01803
2
<−+
aa
⇔
0
)
12
)(
15
(
<−+
aa
⇔
⇔
1215 <<−
a
.
Òàêèì îáðàçîì, èñõîäíîå íåðàâåíñòâî ñâîäèòñÿ ê ñèñòåìå:
2
2
6515,
6512
xx
xx
−+>−
−+<
⇔
<−−
>+−
.076
,0206
2
2
xx
xx
Ïåðâîå íåðàâåíñòâî ñèñòåìû âåðíî ïðè âñåõ çíà÷åíèÿõ õ, à âòî-
ðîå ìîæíî ïðèâåñòè ê âèäó
0)7)(1( <−+ xx
.
Îòâåò: (1; 7).
