Chiodi M. An innovative 3D-CFD-Approach towards Virtual Development of Internal Combustion Engines

Подождите немного. Документ загружается.

136 9 3D-CFD-Modeling of the Combustion for SI-Engines

so that this relation in combination with the equation of ideal gas (assuming constant pressure

within the cell) allows closing the equation system.

,,,,,, jBjBjBjUjUjU

TRTR U U

(9.27)

It is important to underline the iterative aspect of this numerical procedure. At the first

iteration in which a cell

is reached by the flame front,

and

are either assumed

to be equal to the temperature of the central node

or they can be estimated; thus,

also the specific heats

and the real gas constants

are evaluated at these initial

temperatures. From these starting values (iteration 0), applying Eqs. 9.24, 9.25 and 9.27, the new

temperatures of the two zones are evaluated and from these the values

and

are calculated

(iteration 1). After few iterations the equation system converges to a plausible solution (see

Figure 9.15).

Moreover, also the adiabatic flame temperature

jadB

in cell

is determined using the

local fluid properties in the unburned zone of the cell. During the calculation a

comparison between the effective burned gas temperature

and the adiabatic flame

temperature

jadB

(as a maximum value) is performed, so that, if necessary the variable

can be numerically limited to

jadB

. Nevertheless, during many years of investigation it has

been seen that

remains always at least 10 K under the value of the adiabatic flame

temperature.

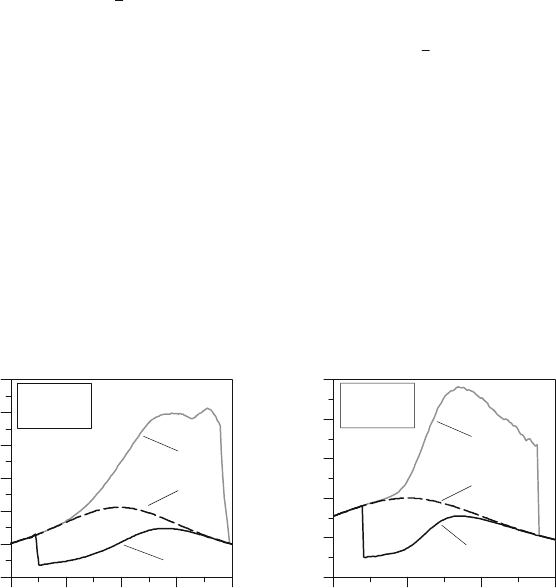
Figure 9.13: Unburned and burned density –

(MB M102-E23)- 1500 rpm - low load –

imep = 3.5 bar.

Figure 9.14: Unburned and burned density –

(MB M102-E23) - 4000 rpm - WOT –

imep = 10.2 bar.

1500 rpm

Low load

Cylinder density, kg/m

Crank an

, de

680 700 FTDC 740 760

4000 rpm

WOT

Cylinder density, kg/m

Crank an

, de

700 FTDC 740 760

9.3 QuickSim’s Approach: Implementation Improvement 137

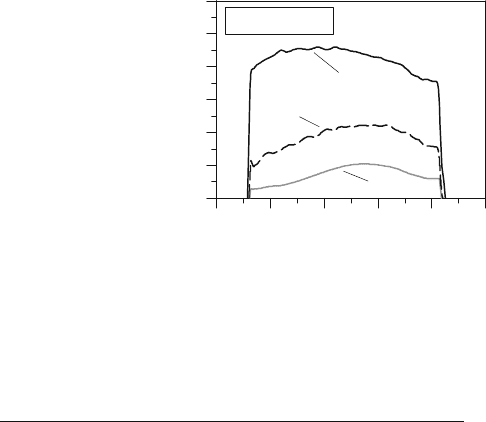
Figure 9.15: Average temperature of the cells at the flame front

(Rotax engine) – 4000 rpm – WOT – imep 10.3 bar.

In Figure 9.15 the profiles of the temperatures as an average over all the cells at the flame front

are reported. As it can be seen, the results of the presented local two-zones-model are plausible.

Comparison: Standard Approach vs. Local Two-Zones Approach

The following comparisons, using the same combustion model, show the differences in the

profiles of the heat-release corrector factor

)(M

(see Chapter 9.3.1) with input variables

either from the standard implementation or from the local two-zones-model. In the standard

implementation the required values are provided by the central node of each cell involved in the

process while in case of the local two-zones-model the required values are conveniently taken

from either the unburned or the burned zones.

The results of two engine simulations at two completely different operating conditions

(see Figures 9.16 and 9.17) show that in case of the two-zones-model the factor

)(M

remains roughly constant during the combustion process. Also the profile of

)(M

c is

quite similar and approximately

1)( #M

in comparison between the presented

simulations.

In case of the standard implementation in contrast,

)(M

shows much wider variations during

the combustion process and also from simulation to simulation, i.e. in this case an overall

correction factor, to be implemented in the combustion model, would not have a general validity.

Using flame propagation models, the calibration of the heat-release rate, independent from the

implementation procedure, is usually performed by the help of a corrector factor

comb

applied to

the turbulence velocity to be introduced in Eq. 9.7:

U_FF

B_FF

Temp. at the flame front, K

500

1000

1500

2000

2500

3000

3500

Crank an

,de

680 700 FTDC 740 760 780

4000 rpm WOT

138 9 3D-CFD-Modeling of the Combustion for SI-Engines



uAvv

combT



(9.28)

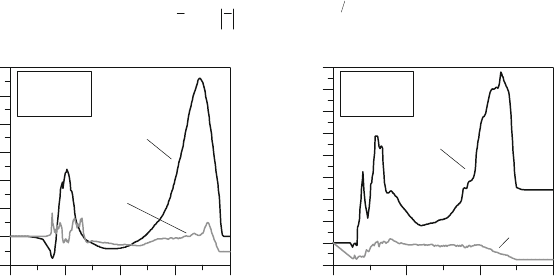
Figure 9.16: Heat-release corrector

factor



. (MB M102-E23)

1500 rpm - low load – imep = 3.5 bar.

Figure 9.17: Heat-release corrector

factor



. (Rotax engine)

4000 rpm - WOT – imep = 10.3 bar.

Of course, also using the standard implementation procedure, it is practically always

possible to fix a reasonable calibration constant

comb

A . This constant allows a matching,

for a given mesh and a more or less wide range of operating conditions, at least

for the combustion duration and the position of 50% burned mass. The determination of

comb

is actually a compromising solution for all local inaccuracies at the flame front,

but often it does not permit a sufficient predictability of the combustion model out

of the calibration range. In contrast the local two-zones-approach allows the following

enhancements:

minor effort in the calibration of the combustion model

a more reliable global and local flame propagation (less mesh dependence)

a better predictability also for complex combustion strategies (e.g. stratified mixture)

a more reliable description of the flame front is available also for other 3D-CFD-models

(e.g. local self ignition models).

Since very often a quite irregular profile of the corrector factor

)(M

remains in the first stage

of the flame development after the ignition (see Figures 9.16 and 9.17), during the years, an

improvement towards a more reliable prediction during this combustion phase has been

achieved. Below the concept idea of this improvement is reported.

1500 rpm

Low Load

Standard

Two-Zones

Model

Burn-rate corrector c

, -

Crank an

, de

680 700 FTDC 740 760

4000 rpm

WOT

Standard

Two-Zones

Model

Burn-rate corrector c

, -

Crank an

, de

690 FTDC 750 780

9.3 QuickSim’s Approach: Implementation Improvement 139

Also at the end of the combustion the corrector factor

)(M

shows some irregularities. Here

the remaining fresh charge mass is very small and the burn rate is low (see Figure 9.9) so that the

effects on the combustion profile are much less sensitive then at the beginning of the flame

propagation. Further models for a better calculation of the flame propagation within the cells in

the wall-near region (mainly responsible for the profile of

)(M

at the end of the combustion)

are already in the development phase.

9.3.4 Ignition Model

After the spark ignition the flame starts propagating from an initial flame kernel generated

by the energy release of the electric arc (plasma region). At the beginning the

flame propagates with a relative laminar flame speed

through the unburned zone

and when the flame front has reached a dimension comparable to the

turbulent eddies it accelerates to the turbulent flame speed

. As introduced in

Chapter 9.3.3 (see Figures 9.16 and 9.17), independently of the local discretization

degree of the mesh, the flame is always numerically very sensitive. The flame starts

propagating within few cells and for a while (ca. 10 deg) it has a dimension not comparable

to the average discretization length of the cells in the spark plug region. Therefore

the prerequisites for a reliable calculation of the local flow field and consequently

the flame propagation are not given.

Up to a certain radius

(usually

4-5 mm) the flame front can be assumed spherical

with good accuracy, thus it is convenient to introduce a phenomenological approach

based on a quasi-dimensional model for the real working-process analysis in this early flame

development. As mentioned in Chapter 4.4.3.2 the main limitations of these quasi-dimensional

models are in the determination of the flame front shape when, reaching a

considerable dimension (usually

8-10 mm), the flame interacts with the

walls of the combustion chamber. That means that as long as the flame propagates

either spherically or half spherically the predictability of the quasi-dimensional model, in

particular in this case where relevant input variables can be detected from the

3D-CFD-simulation, is very good.

Similarly to the wall heat-transfer calculation (see Chapter 10.2.5) an “internal coupling”

between the 3D-CFD-simulation and a phenomenological quasi-dimensional model is

established (see Figure 9.18). This procedure, as a “closed loop”, allows to control the flame

propagation in the 3D-CFD-simulation using a phenomenological spherical kernel growth with a

given flame speed (laminar and turbulent) as a target value.

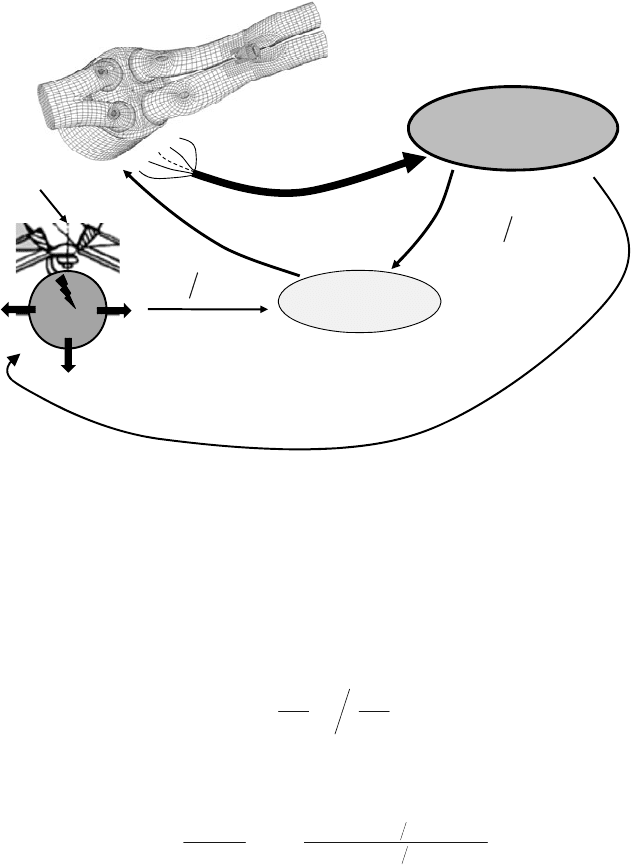
140 9 3D-CFD-Modeling of the Combustion for SI-Engines

Figure 9.18: The “internal coupling” between a 3D-CFD-code and

a phenomenological quasi-dimensional model for early flame propagation.

The control is performed by a correction factor



IgHR

(see Figure 9.18) that adjusts the

flame propagation at each time-step up to

4-5 mm (after reaching this radius the

combustion model switches to the common procedure). The controlling relation (in this case

using as output variable the related heat-release) becomes:



CFD

IgHR

(9.29)

Starting with the definition of the flame kernel volume



IgB

as a sum of the local burned

zone of the involved cells (

IgB

Nj 

)



UU

UU

S

,,,,

,,,

IgB

jBjBjUjB

jjBjUjB

IgB

(9.30)

Evaluation

Tool

Comparison

)(

IgHR







,,,,

xvxT





CFD

ddQ M



.Ph

ddQ M

3D-CFD-Simulation

Phenomenological

kernel propagation

(spark plug region)

Spark plug

 



,

SPSP

9.3 QuickSim’s Approach: Implementation Improvement 141

and applying the two-zones-model presented in Chapter 9.3.3, it is then possible to calculate the

target heat release for a flame propagation with a relative flame speed

. The specific

heat release term

is calculated according Chapter 8.4.2.1:

/ HRTLUKHRTLfU

hSrhSA

'US 'U

(9.31)

Finally it is possible also to calculate the absolute flame speed

IgB

S

(9.32)

so that a comprehensive evaluation and control of the flame propagation during the early flame

development can be performed.

9.3.5 Final Implementation Procedure

The combustion model presented in this chapter is based on the Weller formulation.

The implementation within the 3D-CFD-code

QuickSim has been performed choosing

input variables able to give reliability to the fuel heat release over a wide range of engine

operating conditions and trying to reduce as much as possible the dependence of the mesh on the

results.

In this section the numerical implementation procedure of each variable is briefly described..

Laminar Flame Speed

The laminar flame speed

according to the proposed combustion model is the basic variable

for the calculation of the final flame propagation. Starting with the formulation introduced with

Eqs. 4.17 and 4.18, the local calculation of

in a cell

within the flame front takes the

following input variables into account:

),,,(

,_,, jUEGRjUjFreshL

wTpfS O

(9.33)

where

jFresh,

and

jUEGR ,_

are easily obtained using the local scalar values of the species

(see Chapter 8.4). The local temperature of the unburned zone

is provided by the two-

zones-model introduced in this chapter. Since the pressure

in the cylinder is almost constant

during the working period, there is no need to use the local value

, i.e. the spatial-average

142 9 3D-CFD-Modeling of the Combustion for SI-Engines

pressure

is directly provided to the calculation model of

by the evaluation tool of

QuickSim (see Chapters 7.4 and 10.2.4).

Turbulent Term

In the formulation of the turbulent term (see Eq. 9.28) the local fluid velocity in each cell at the

flame front is taken as a reference for the variable

Regarding the description of the turbulent velocity

, the procedure is more complex. As

already mentioned in this work the turbulence is a very sensitive variable with the mesh quality

(more details in Chapter 10.2.4.1), i.e. the local value of the turbulence can often be an

“unreliable” input variable.

The problem can be pragmatically solved using a filtered result of the turbulence.

Therefore in the cells at the flame front the relevant turbulence value

for the

combustion model is calculated using a weighting factor

turb

that mixes the local

turbulent velocity

local

with the average value over the whole unburned zone

(see

Figure 9.19).



Uturblocalturb

uCuCu





(9.34)

Depending on an estimation of the mesh quality during the whole simulation (the

evaluation tool of

QuickSim automatically provides mesh quality indexes, like

average aspect ratio, warpage angle, etc.) the factor

turb

usually varies between 0.5 and 0.7.

This factor can also be set selectively in the different regions of the combustion

chamber. Exemplarily in the cells in the near-wall region, where the turbulence is extremely

sensible with the mesh quality, it is often convenient to use locally very low values of

turb

(~0.1-0.3).

Since a too high value of the turbulence may cause a local flame extinction (see Chapter 9.1), if

the ratio

exceeds critical values provided by the internal flame quenching models, the

local burn rate can be either reduced or completely deactivated.

Turbulent Length Scale

A similar procedure adopted for the turbulence is used here also for the description of the

relevant turbulent length scale

l for the combustion model.



Ultlslocalltlsl

lClCl

1 

(9.35)

9.4 Results 143

Therefore in the cells at the flame front

is calculated using a weighting factor

tls

that mixes

the local turbulence length scale

locall

with the average value over the whole unburned zone

(see Figure 9.20). The influence of the turbulent length scale on the local burn rate is

less relevant then the turbulence, what allows the usage of relatively high values of

tls

(~0.7-0.9).

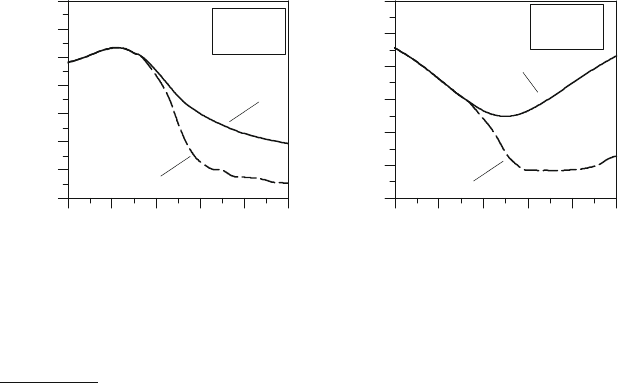
Figure 9.19: Turbulent velocity –

(MB M102-E23) - 4000 rpm - WOT –

imep = 10.2 bar.

Figure 9.20: Turbulent length scale –

(MB M102-E23) - 4000 rpm - WOT –

imep = 10.2 bar.

Flame Radius

The required flame radius

is at disposal from the evaluation tool of QuickSim and is

directly implemented in the formulation of Weller’s combustion model within a “closed

loop”.

9.4 Results

Figures 9.21 and 9.22 show the result of the cylinder pressure profile in the Rotax

engine using the proposed implementation of the combustion model without

additional adjustments for the different operating conditions (i.e. the same

comb

has been

used).

4000 rpm

WOT

Unburned

zone

Cyl. average

Turbulent velocity u', m/s

Crank an

, de

660 690 FTDC 750 780 810

4000 rpm

WOT

Unburned

zone

Cyl. average

Cyl. turb. length scale l

, mm

0.0

0.5

1.0

1.5

2.0

2.5

3.0

Crank an

, de

660 690 FTDC 750 780 810

144 9 3D-CFD-Modeling of the Combustion for SI-Engines

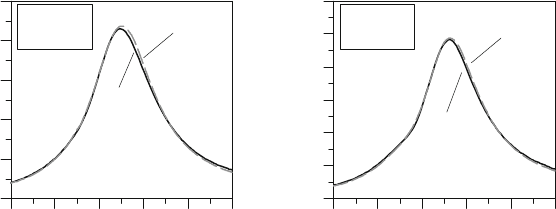
Figure 9.21: Cylinder pressure.

Comparison 3D-Ph. vs. Exp. - (Rotax)

1500 rpm - low load – imep = 4.0 bar.

Figure 9.22: Cylinder pressure.

Comparison 3D-Ph. vs. Exp. - (Rotax)

4000 rpm - WOT – imep = 10.3 bar.

The comparisons with experimental data show a very good accuracy at both operating

conditions, which remarkably differ in terms of engine speed and load.

1500 rpm

Low Load

3D-CFD

Exp.

Cylinder pressure p, bar

Crank an

, de

660 690 FTDC 750 780 810

4000 rpm

WOT

3D-CFD

Exp.

Cylinder pressure p, bar

Crank an

, de

660 690 FTDC 750 780 810

3D-CFD-Modeling of the

Wall Heat-Transfer

The wall heat-transfer represents the thermodynamic boundary condition of the combustion

chamber and, in particular during the working period, is the main source of inaccuracy in the

3D-CFD-analysis of the engine operating cycle.

Very often in the 3D-CFD-simulation attention is mainly paid to the modeling of phenomena

like combustion (chemical kinetic reactions) and fuel spray formation, instead of ensuring an

accurate balance in the solution of all relevant engine processes. This is a fatal error that easily

compromises the quality of the simulation results because a simulation running with wrong

thermodynamic boundary conditions will never deliver reliable results.

10.1 Introduction

During the last 50 years the heat-transfer process between the working fluid and the combustion

chamber walls and its noticeable effects on engine performance, efficiency and emissions have

been intensively experimentally investigated and reported. The heat transfer is one of the major

factors affecting the engine energy balance at any operating condition. Considering exemplary a

common natural aspirated SI engine [5,7,26,40,71-86] (see Figure 3.2), the ratio of heat transfer

to the fuel heating energy is approximately 20 – 25 % for full load and even more than 30 % for

low load, respectively. Therefore, a high accuracy in the determination of the engine heat

transfer is a prerequisite for a realistic computational analysis according, at least, to the engine

energy balance.

In comparison to other engine processes, whose evaluation can be easily proved with reference

values (e.g. during the combustion the heat release will never exceed 100% of the fuel heat-

M. Chiodi, An Innovative 3D-CFD-Approach towards Virtual Development of

Internal Combustion Engines, DOI 10.1007/978-3-8348-8131-1_10,