Черный А.А. Основы изобретательства и научных исследований

101

()

22224

1

2

,

4

1

,

mrdmrcmrbmra

dmrdcmrcbmrbamra

u

umr

u

uumr

mr

xxxx

yxyxyxyx

x

yx

b

+++

⋅+⋅+⋅+⋅

=

⋅

=

∑

=

; (39)

()

22224

1

2

,

4

1

,

msdmscmsbmsa

dmsdcmscbmsbamsa

u

ums

u

uums

ms

xxxx

yxyxyxyx

x

yx

b

+++

⋅+⋅+⋅+⋅

=

⋅

=

∑

=

; (40)

{

}

{}

ysbs

2'

0

2

4

1

⋅= ;

{}

{

}

(

)

222222

/

mndmncmnbmnamn

xxxxysbs +++=

,

{}

{

}

(

)

222222

/

mrdmrcmrbmramr

xxxxysbs +++= ,

{}

{

}

(

)

222222

/

msdmscmsbmsams

xxxxysbs +++= ,

где s

2

{y} - дисперсия опытов; s

2

{b

′

o

}, s

2

{b

mn

}, s

2

{b

mr

}, s

2

{b

ms

} – дисперсии в

определении соответствующих коэффициентов регрессии

b

′

o

, b

mn

, b

mr

, b

ms

.

В многочлене (30) последующий член имеет на один коэффициент

ортогонализации больше, чем предыдущий член. Так, второй член имеет

один коэффициент ортогонализации, третий член – два, четвертый член –

три коэффициента ортогонализации, а всего получилось шесть коэффици-

ентов ортогонализации, причем по мере увеличения количества коэффици-

ентов ортогонализации усложняются формулы для расчета этих коэффи-

циентов.

Важной особенностью уравнения регрессии (30) и матрицы плани-

рования (см. табл.28) является их универсальность в связи с возможностью

изменения чисел показателей степени факторов и перехода в частном слу-

чае к планированию на двух уровнях факторов.

Математические модели процессов сначала следует выявлять при

показателях степени факторов

n = 1, r = 2, s = 3, а если при этом матема-

тические модели не обеспечивают требуемой точности, то показатели сте-

пени факторов необходимо изменять, добиваясь требуемой точности.

Применяя дифференцирование функций или графические построе-

ния, можно найти максимумы или минимумы этих функций.

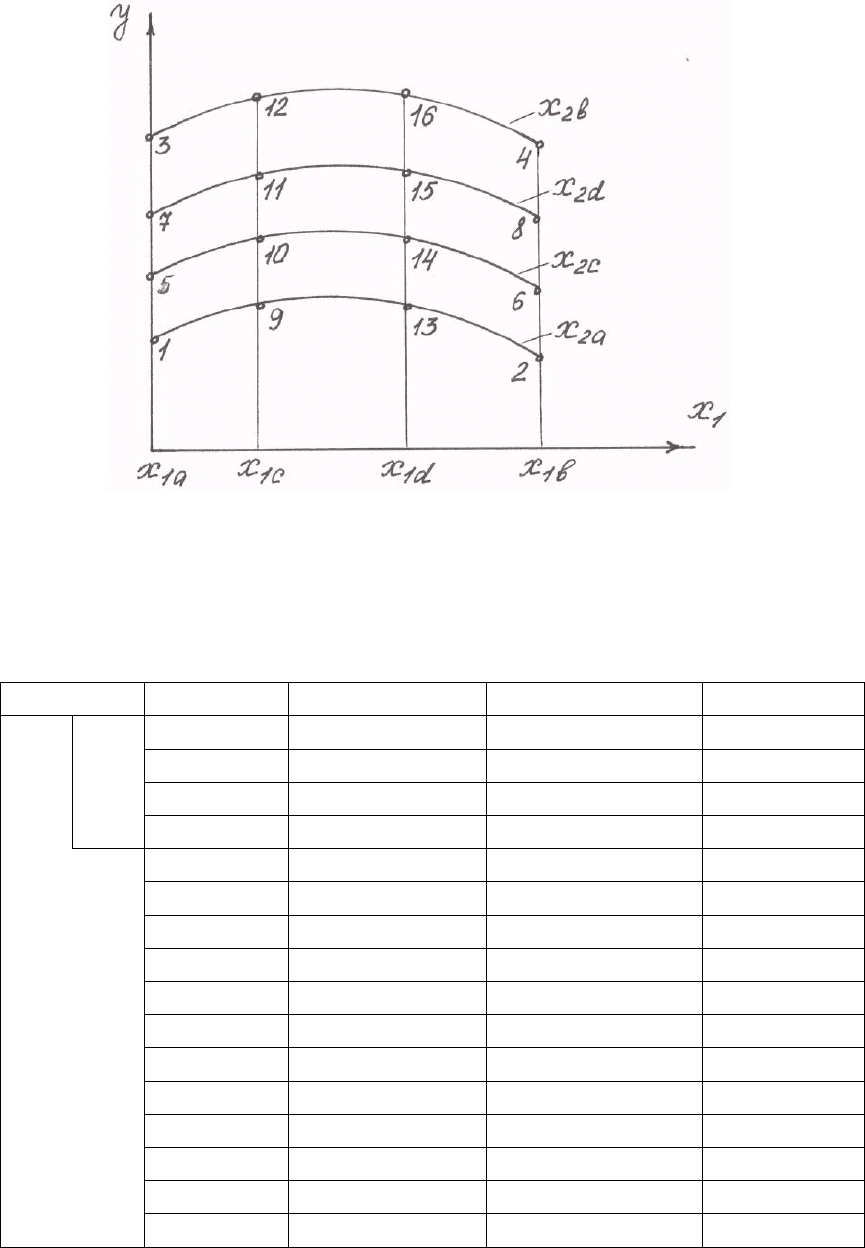
На рис. 18 представлена в общем виде графическая зависимость по-

казателя от двух факторов при планировании 4

2

.

Если записать в виде таблицы координаты точек 1-16 (рис. 18), то

получается план проведения двухфакторных экспериментов на четырех, и

в частном случае, на двух уровнях независимых переменных (табл. 29).

102

Рис.18. Зависимость показателя от двух факторов при

планировании 4

2

Таблица 29

Планы проведения двухфакторных экспериментов 4

2

и 2

2

План №, u

x

1,u

x

2,u

y

u

1

x

1,1

=x

1a

x

2,1

=x

2a

y

1

2

x

1,2

=x

1b

x

2,2

=x

2a

y

2

3

x

1,3

=x

1a

x

2,3

=x

2b

y

3

2

4

x

1,4

=x

1b

x

2,4

=x

2b

y

4

5

x

1,5

=x

1a

x

2,5

=x

2c

y

5

6

x

1,6

=x

1b

x

2,6

=x

2c

y

6

7

x

1,7

=x

1a

x

2,7

=x

2d

y

7

8

x

1,8

=x

1b

x

2,8

=x

2d

y

8

9

x

1,9

=x

1c

x

2,9

=x

2a

y

9

10

x

1,10

=x

1c

x

2,10

=x

2c

y

10

11

x

1,11

=x

1c

x

2,11

=x

2d

y

11

12

x

1,12

=x

1c

x

2,12

=x

2b

y

12

13

x

1,13

=x

1d

x

2,13

=x

2a

y

13

14

x

1,14

=x

1d

x

2,14

=x

2c

y

14

15

x

1,15

=x

1d

x

2,15

=x

2d

y

15

4

2

16

x

1,16

=x

1d

x

2,16

=x

2b

y

16

103

Для плана 4

2

уравнение регрессии определяются исходя из соответ-

ствующих зависимостей:

y = a

′

o

+ a

1n

⋅

x

1n

+ a

1r

⋅

x

1r

+ a

1s

⋅

x

1s

,

где a

′

o

= c

′

o

⋅

x

o

+ c

2n

⋅

x

2n

+ c

2r

⋅

x

2r

+ c

2s

⋅

x

2s

;

a

1n

= d

′

o

+ d

2n

⋅

x

2n

+ d

2r

⋅

x

2r

+ d

2s

⋅

x

2s

;

a

1r

= e

′

o

+ e

2n

⋅

x

2n

+ e

2r

⋅

x

2r

+ e

2s

⋅

x

2s

;

a

1s

= f

′

o

+ f

2n

⋅

x

2n

+ f

2r

⋅

x

2r

+ f

2s

⋅

x

2s

.

После подстановки, перемножений и замены коэффициентов полу-

чается следующий полином для плана 4

2

(см. табл. 29):

y = b

′

o

⋅

x

o

+ b

1n

⋅

x

1n

+ b

2n

⋅

x

2n

+ b

1n,2n

⋅

x

1n

⋅

x

2n

+ b

1r

⋅

x

1r

+ b

2r

⋅

x

2r

+

+ b

1n,2r

⋅

x

1n

⋅

x

2r

+ b

2n,1r

⋅

x

2n

⋅

x

1r

+ b

1r,2r

⋅

x

1r

⋅

x

2r

+ b

1s

⋅

x

1s

+ b

2s

⋅

x

2s

+

+ b

1n,2s

⋅

x

1n

⋅

x

2s

+ b

2n,1s

⋅

x

2n

⋅

x

1s

+ b

1r,2s

⋅

x

1 r

⋅

x

2s

+ b

2r,1s

⋅

x

2r

⋅

x

1s

+

+ b

1s,2s

⋅

x

1s

⋅

x

2s

(41)

В уравнении регрессии (41)

y - показатель (параметр) процесса;

x

o

= + 1; x

1n

= x

n

1

+ v

1

;

x

1r

= x

r

1

+ a

1

⋅

x

n

1

+ c

1

; x

1s

= x

s

1

+ d

1

⋅

x

r

1

+ e

1

⋅

x

n

1

+ f

1

;

x

2n

=x

n

2

+ v

2

; x

2r

= x

r

2

+ a

2

⋅

x

n

2

+ c

2

;

x

2s

= x

s

2

+ d

2

⋅

x

r

2

+ e

2

⋅

x

n

2

+ f

2

;

x

1

, x

2

- 1, 2-й факторы (независимые переменные); n, r, s, -изменяемые чис-

ла показателей степени факторов;

v

1

, a

1

, c

1

, d

1

, e

1

, f

1

- коэффициенты орто-

гонализацииции, определяемые при четырех уровнях 1-го фактора,

m = 1,

по формулам (31) - (36);

v

2

,a

2

, c

2

, d

2

, e

2

, f

2

, - коэффициенты ортогонализа-

ции, определяемые при четырех уровнях 2-го фактора,

m = 2, по формулам

(31)-(36);

b

0

′

, b

1n

, b

2n

, b

1n,2n

, b

1r

, b

2r

, b

1n,2r

, b

2n,1r

, b

1r,2r

, b

1s

, b

2s

, b

1n,2s

, b

2n,1s

, b

1r,2s

, b

2r,1s

,

b

1s,2s

, - коэффициенты регрессии. Для уровней a, b, c, d факторы имеют

следующие обозначения:

x

1a

, x

1b

, x

1c

, x

1d

, x

2a

, x

2b

, x

2c

, x

2d

.

В связи с ортогональным планированием все коэффициенты регрес-

сии и дисперсии в их определении рассчитываются независимо друг от

друга. Формулы для расчета коэффициентов регресcии уравнения (41)

имеют следующий вид:

;

N

y

x

yx

b

N

u

N

u

u,o

u

N

u

u,o

'

∑

=

⋅

=

1

2

1

0

;

x

yx

b

N

u

u,n

u

N

u

u,n

n

∑

=

⋅

=

1

2

1

104

;

x

yx

b

N

u

u,n

u

N

u

u,n

n

∑

=

⋅

=

1

2

1

2

;

)xx(

yxx

b

N

u

u,n

uu,n

N

u

u,n

n,n

∑

=

⋅

⋅⋅

=

1

2

1

2

1

21

;

x

yx

b

N

u

u,r

u

N

u

u,r

r

∑

=

⋅

=

1

2

1

;

x

yx

b

N

u

u,r

u

N

u

u,r

r

∑

=

⋅

=

1

2

1

2

;

)xx(

yxx

b

N

u

u,r

u,n

u

N

u

u,ru,n

r,n

∑

=

⋅

⋅⋅

=

1

2

1

21

;

)xx(

yxx

b

N

u

u,r

u,n

u

N

u

u,ru,n

r,n

∑

=

⋅

⋅⋅

=

1

2

1

2

1

12

;

)xx(

yxx

b

N

u

u,r

u

N

u

u,ru,r

r,r

∑

=

⋅

⋅⋅

=

1

2

1

21

;

x

yx

b

N

u

u,s

u

N

u

u,s

s

∑

=

⋅

=

1

2

1

;

x

yx

b

N

u

u,s

u

N

u

u,s

s

∑

=

⋅

=

1

2

1

2

;

)(

,

,,

,

∑

=

⋅

⋅⋅

=

N

u

us

un

u

N

u

usun

sn

xx

yxx

b

1

2

1

21

;

)xx(

yxx

b

N

u

u,s

u,n

u

N

u

u,su,n

s,n

∑

=

⋅

⋅⋅

=

1

2

1

2

1

12

;

)xx(

yxx

b

N

u

u,s

u,r

u

N

u

u,su,r

s,r

∑

=

⋅

⋅⋅

=

1

2

1

21

;

)xx(

yxx

b

N

u

u,s

u,r

u

N

u

u,su,r

s,r

∑

=

⋅

⋅⋅

=

1

2

1

2

1

12

;

)xx(

yxx

b

N

u

u,s

u

N

u

u,su,s

s,s

∑

=

⋅

⋅⋅

=

1

2

1

21

где

x

1n,u

= x

n

1,u

+ v

1

; x

1r,u

= x

r

1,u

+ a

1

⋅

x

n

1,u

+ c

1

;

x

1s,u

= x

s

1,u

+ d

1

⋅

x

r

1,u

+ e

1

⋅

x

n

1,u

+ f

1

;

105

x

2n,u

= x

n

2,u

+ v

2

; x

2r,u

= x

r

2,u

+ a

2

⋅

x

n

2,u

+ c

2

;

x

2s,u

= x

s

2,u

+ d

2

⋅

x

r

2,u

+ e

2

⋅

x

n

2,u

+ f

2

;

N

– количество опытов в соответствующем уравнению регрессии

плане проведения экспериментов, т.е.

N = 16 для плана 4

2

.

Выполняется расчет тех коэффициентов регрессии, которые входят в

рассматриваемое уравнение регрессии.

Если числитель (делимое) каждой из формул для расчета коэффици-

ентов регрессии заменить величиной дисперсии опытов

s

2

{y}, а знамена-

тель (делитель) оставить прежним, то получаются формулы для расчета

дисперсий в определении соответствующих коэффициентов регрессии

s

2

{b

'

0

}, s

2

{b

1n

}, s

2

{b

2n

}, s

2

{b

1n,2n

}, s

2

{b

1r

}, s

2

{b

2r

}, s

2

{b

1n,2r

}, s

2

{b

2n,1r

}, s

2

{b

1r,2r

},

s

2

{b

1s

}, s

2

{b

2s

}, s

2

{b

1n,2s

}, s

2

{b

2n,1s

}, s

2

{b

1r,2s

}, s

2

{b

2r,1s

}, s

2

{b

1s,2s

}.

Сначала следует принимать n = 1, r = 2, s = 3 и при этих числах по-

казателей степени факторов производить расчет коэффициентов регрессии,

дисперсий в их определении, выявлять статистически значимые коэффи-

циенты регрессии. После подстановки в уравнение регрессии статистиче-

ски значимых и не равных нулю коэффициентов регрессии надо выявлять

точность математической зависимости. Если при проверке выясняется, что

математическая зависимость не обеспечивает

требуемой точности, то сле-

дует изменить величины показателей степени факторов и снова выполнять

расчеты, пока не будет достигнута требуемая точность.

В табл. 30 и 31 представлены планы 4

1

(Х = 4) и 4

2

(Х = 16) с обозна-

чение факторов и показателей применительно к компьютерным програм-

мам. Величина Х соответствует количеству опытов по плану и является

управляющим параметром в программах,

A1 = x

1a

, B1 = x

1b

, C1 = x

1c

, D1 =

x

1d

, A2 = x

2а

, B2 = x

2b

, C2 = x

2c

, D2 = x

2d

, показатели Y(J) соответствуют у

и

.

Таблица 30

План 4

1

(Х = 4)

Номер фактора Фактор

F(J) Показатель Y(J)

1

A1 Y(1)

2

B1 Y(2)

3

C1 Y(3)

4

D1 Y(4)

106

Таблица 31

План 4

2

(Х = 16)

Факторы

Номер опыта

F(J) H(J)

Показатель

Y(J)

1

A1 A2 Y(1)

2

B1 A2 Y(2)

3

A1 B2 Y(3)

4

B1 B2 Y(4)

5

A1 C2 Y(5)

6

B1 C2 Y(6)

7

A1 D2 Y(7)

8

B1 D2 Y(8)

9

С1 A2 Y(9)

10

С1 C2 Y(10)

11

С1 D2 Y(11)

12

С1 B2 Y(12)

13

D1 A2 Y(13)

14

D1 C2 Y(14)

15

D1 D2 Y(15)

16

D1 B2 Y(16)

Многофакторное математическое моделирование можно выполнять

на основе планов

3 · к + 1, где к – количество факторов, оказывающих

влияние на показатель процесса. В этом случае количество уровней каждо-

го фактора – четыре. Уровни

x

md

- общие и определяются как средние

арифметические величины

D1 = x

1d

= 0,5 · (x

1a

+ x

1b

);

D2 = x

2d

= 0,5 · (x

2a

+ x

2b

);

D3 = x

3d

= 0,5 · (x

3a

+ x

3b

);

D4 = x

4d

= 0,5 · (x

4a

+ x

4b

);

D5 = x

5d

= 0,5 · (x

5a

+ x

5b

).

В табл. 32-35 приведены планы 3 · к + 1 соответственно для случаев,

когда

к = 2; к = 3; к = 4; к = 5. Математические модели выявляются как

для однофакторного процесса при планировании на четырех уровнях каж-

дого фактора. Получаются системы уравнений, в которых столько уравне-

ний, сколько принято факторов, оказывающих влияние на показатель про-

цесса. По мере увеличения количества факторов в плане необходимо уве-

личивать количество проводимых опытов (при увеличении

к на 1 увеличи-

вается количество опытов на 3).

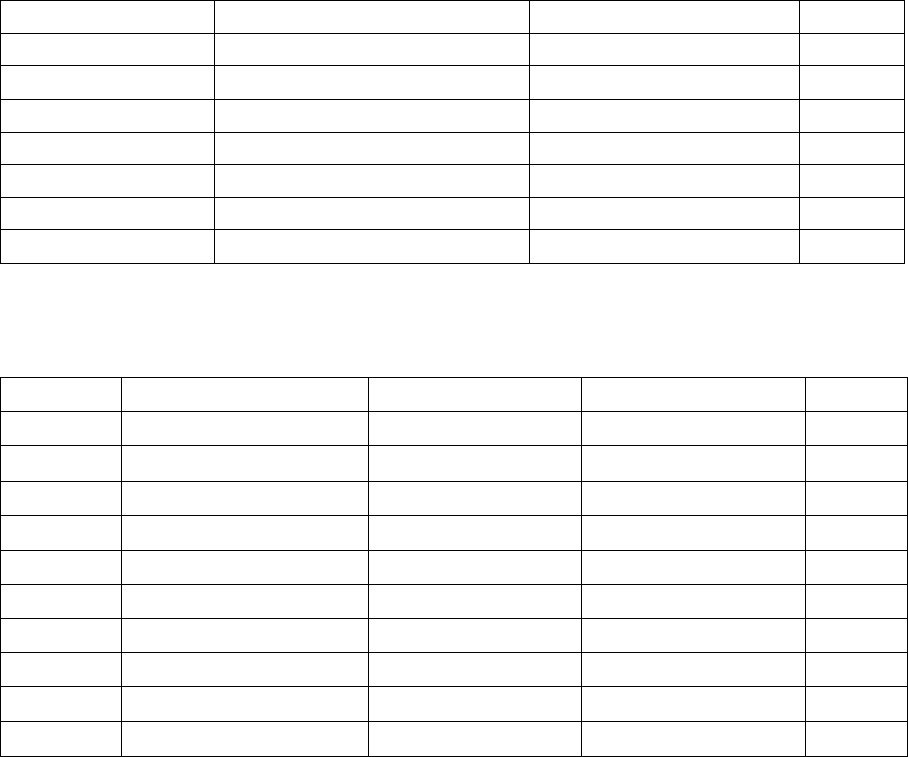
На рис. 19 показана схема зависимости показателя от факторов при

планировании

3 · к + 1, когда к = 5.

107

Таблица 32

План

3 · к + 1 при к = 2

№ х

1

х

2

у

1 A1 = x

1a

D2 Y(1)

2 B1 = x

1b

D2 Y(2)

3 C1 = x

1c

D2 Y(3)

4 D1 A2 = x

2a

Y(1)

5 D1 B2 = x

2b

Y(2)

6 D1 C2 = x

2c

Y(3)

7 D1 D2 Y(4)

Таблица 33

План

3 · к + 1 при к = 3

№ х

1

х

2

х

3

у

1 A1 = x

1a

D2 D3 Y(1)

2 B1 = x

1b

D2 D3 Y(2)

3 C1 = x

1c

D2 D3 Y(3)

4 D1 A2 = x

2a

D3 Y(1)

5 D1 B2 = x

2b

D3 Y(2)

6 D1 C2 = x

2c

D3 Y(3)

7 D1 D2 A3 = x

3a

Y(1)

8 D1 D2 B3 = x

3b

Y(2)

9 D1 D2 C3 = x

3c

Y(3)

10 D1 D2 D3 Y(4)

108

Таблица 34

План

3 · к + 1 при к = 4

№ х

1

х

2

х

3

х

4

у

1

A1 = x

1a

D2 D3 D4 Y(1)

2

B1 = x

1b

D2 D3 D4 Y(2)

3

C1 = x

1c

D2 D3 D4 Y(3)

4

D1 A2 = x

2a

D3 D4 Y(1)

5

D1 B2 = x

2b

D3 D4 Y(2)

6

D1 C2 = x

2c

D3 D4 Y(3)

7

D1 D2 A3 = x

3a

D4 Y(1)

8

D1 D2 B3 = x

3b

D4 Y(2)

9

D1 D2 C3 = x

3c

D4 Y(3)

10

D1 D2 D3 A4 = x

4a

Y(1)

11

D1 D2 D3 B4 = x

4b

Y(2)

12

D1 D2 D3 C4 = x

4c

Y(3)

13

D1 D2 D3 D4 Y(4)

Таблица 35

План

3 · к + 1 при к = 5

№ х

1

х

2

х

3

х

4

х

5

у

1

A1 = x

1a

D2 D3 D4 D5 Y(1)

2

B1 = x

1b

D2 D3 D4 D5 Y(2)

3

C1 = x

1c

D2 D3 D4 D5 Y(3)

4

D1 A2 = x

2a

D3 D4 D5 Y(1)

5

D1 B2 = x

2b

D3 D4 D5 Y(2)

6

D1 C2 = x

2c

D3 D4 D5 Y(3)

7

D1 D2 A3 = x

3a

D4 D5 Y(1)

8

D1 D2 B3 = x

3b

D4 D5 Y(2)

9

D1 D2 C3 = x

3c

D4 D5 Y(3)

10

D1 D2 D3 A4 = x

4a

D5 Y(1)

11

D1 D2 D3 B4 = x

4b

D5 Y(2)

12

D1 D2 D3 C4 = x

4c

D5 Y(3)

13

D1 D2 D3 D4 A5 = x

5a

Y(1)

14

D1 D2 D3 D4 B5 = x

5b

Y(2)

15

D1 D2 D3 D4 C5 = x

5c

Y(3)

16

D1 D2 D3 D4 D5 Y(4)

109

Рис. 19. Схема зависимости показателя от пяти факторов

при планировании 3 · 5 + 1

Математическое моделирование при планировании

3 · к + 1 рацио-

нально проводить, когда необходимо выявить ряд факторов, оказывающих

существенное влияние на показатель процесса. Это моделирование выпол-

няется на основе небольшого количества экспериментальных данных, но

позволяет прогнозировать улучшение процессов, определять, при каких

условиях можно достигать оптимальных результатов.

При проведении двухфакторных экспериментов нередко возни-

кают случаи, когда рационально принимать неодинаковое количество

уровней первого и второго независимых переменных. На рис. 20 представ-

лены для общих случаев различные варианты графических зависимостей

параметра от двух факторов. В соответствии с графиками рис. 20 экспери-

менты можно планировать, принимая для первого фактора три, четыре,

пять уровней, а для второго фактора соответственно четыре, пять, три

уровня.

В табл. 36, 37, 38 приведены планы

34

⋅

, 35

⋅

, 45

⋅

, которые являются

частными случаями плана 5

2

. Каждая строчка плана 3⋅4 (см. табл. 36) явля-

ется координатами соответствующей точки графической кривой рис. 20, а.

В плане

35⋅ (см. табл. 37) представлены построчно координаты графиче-

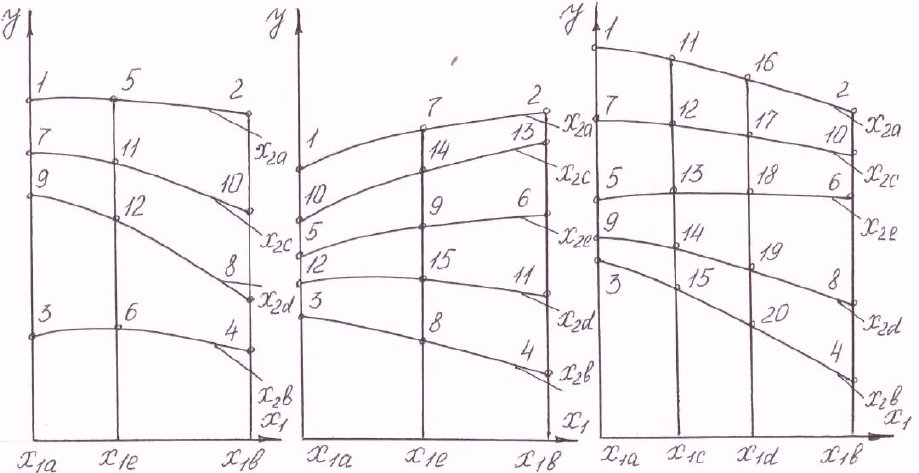
110

ских кривых (рис. 20, б), а в плане 45

⋅

(табл. 38) - координаты графиче-

ских кривых (рис. 20, в).

Планы 3

⋅4, 3⋅5, 4⋅5 являются выборками из плана 5

2

. Они позволя-

ют выявлять математические модели процессов при меньшем количестве

опытов, чем при планировании 5

2

. Сомножители в обозначениях планов

3

⋅4, 3⋅5, 4⋅5 указывают соответственно на количество уровней первого и

второго факторов, а произведения указанных сомножителей - на количест-

во опытов в планах-выборках.

а) б) в)

Рис. 20. Схемы зависимостей показателя от двух факторов

для случаев а) 3·4, б) 3·5, в) 4·5

Черный А.А. Основы изобретательства и научных исследований

Подождите немного. Документ загружается.