Черный А.А. Основы изобретательства и научных исследований
Подождите немного. Документ загружается.

91
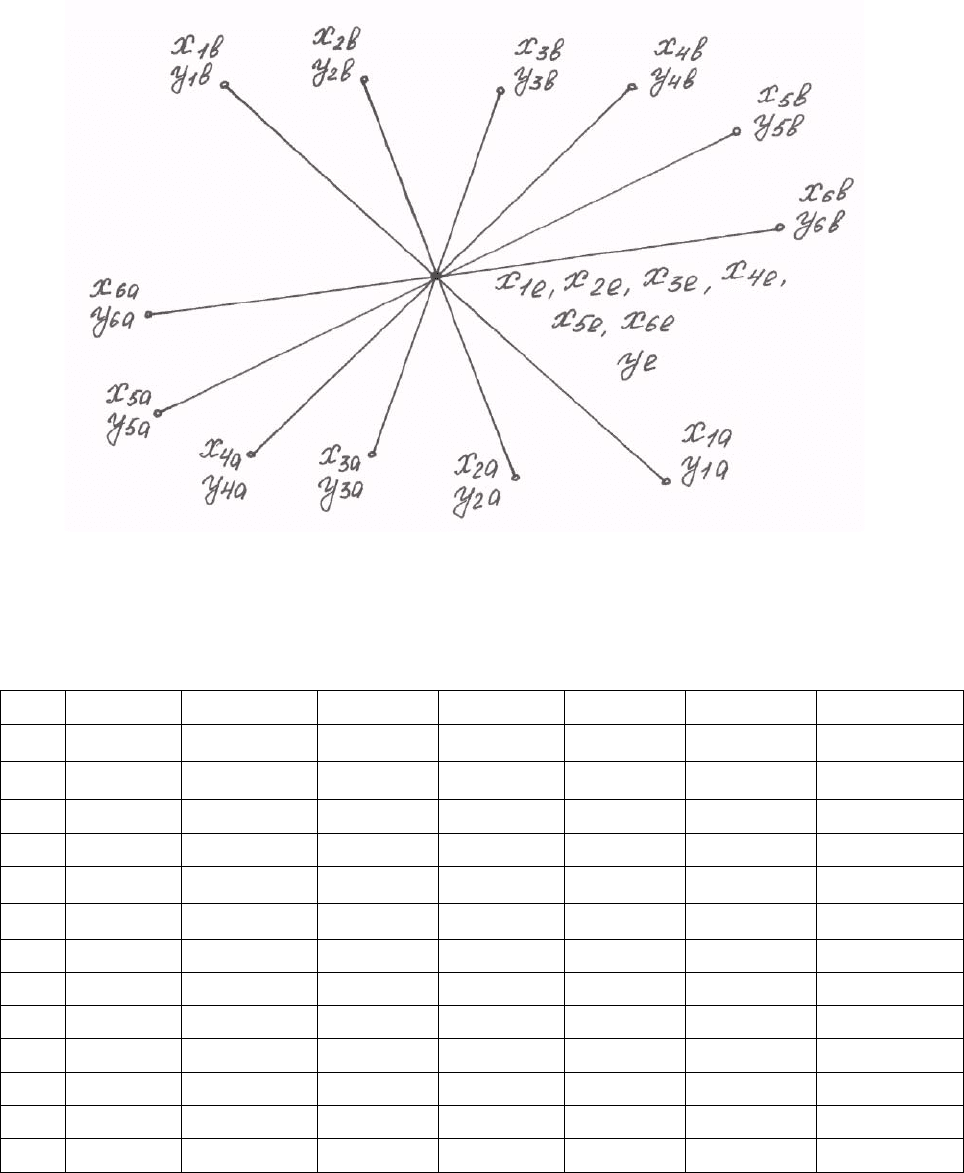
Рис. 17. Схема зависимости показателя от шести факторов
при планировании 2·6 + 1
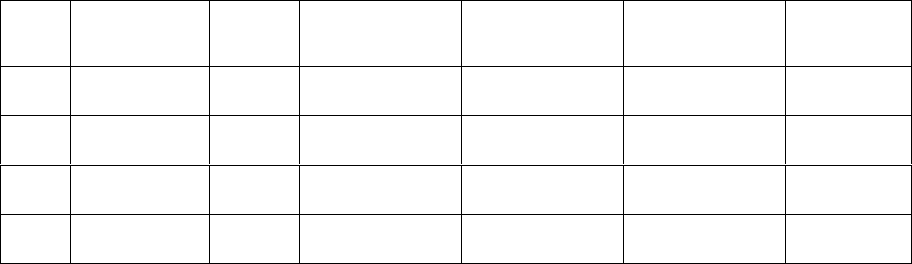
Таблица 27
План 2·к + 1 при к = 6
№
х
1
х
2
х
3
х
4
х
5
х
6
у
1
А1 = х
1а
х
2е
х
3е
х
4е
х
5е
х
6е
Y(1) = у
1а
2
В1 = х
1b
х
2е
х
3е
х
4е
х
5е
х
6е
Y(2) = у
1b
3
х
1е
А1 = х
2а
х
3е
х
4е
х
5е
х
6е
Y(1) = у
2а
4
х
1е
В1 = х
2b
х
3е
х
4е
х
5е
х
6е
Y(2) = у
2b
5
х
1е
х
2е
А1 = х
3а
х
4е
х
5е
х
6е
Y(1) = у
3а
6
х
1е
х
2е
В1 = х
3b
х
4е
х
5е
х
6е
Y(2) = у
3b
7
х
1е
х
2е
х
3е
А1 = х
4а
х
5е
х
6е
Y(1) = у
4а
8
х
1е
х
2е
х
3е
В1 = х
4b
х
5е
х
6е
Y(2) = у
4b
9
х
1е
х
2е
х
3е
х
4е
А1 = х
5а
х
6е
Y(1) = у
5а
10
х
1е
х
2е
х
3е
х
4е
В1 = х
5b
х
6е
Y(2) = у
5b
11
х
1е
х
2е
х
3е
х
4е
х
5е
А1 = х
6а
Y(1) = у
6а
12
х
1е
х
2е
х
3е
х
4е
х
5е
В1 = х
6b
Y(2) = у
6b
13
х
1е
х
2е
х
3е
х
4е
х
5е
х
6е
Y(3) = у
е
92
В ряде случаев рационально применять математическое моделиро-
вание на основе планирования экспериментов на четырех уровнях факто-
ров.
При планировании экспериментов на четырех уровнях независимых
переменных предложено универсальное уравнение регрессии, в общем ви-
де представляющее четырехчлен:
y = b
′
о
⋅
х
о
+ b
mn
· x
mn
+ b
mr
· x
mr
+ b
ms
· x
ms
, (30)
в котором
y – показатель (параметр) процесса; х
о
= +1;
х
mn
= x
n
m
+ v
m
; x
mr
=x
r
m
+a
m
· x
n
m
+c
m
; x
ms
=x
s
m
+ d
m
· x
r
m
+ e
m
· x
n
m
+ f
m
;
m
– порядковый номер фактора; x
m
– m-й фактор (независимое перемен-
ное);
n, r, s – изменяемые числа показателей степени факторов; v
m
, a
m
, c
m
,
d
m
, e
m
, f
m
– коэффициенты ортогонализации; b
′
o
, b
mn
, b
mr
, b
ms
– коэффициен-
ты регрессии.
Для каждой величины
m-го фактора x
ma
, x
mb
, x
mс
, x
md
определяются
соответственно параметры
y
a
, y
b
, y
c
,y
d
.
В табл.28 представлена матрица планирования однофакторных экс-
периментов на четырех уровнях независимых переменных.
Таблица 28
Матрица планирования однофакторных экспериментов
на четырех уровнях независимых переменных
В матрице планирования экспериментов (табл.28):
x
mna
= x
n
ma
+
v
m
; x
mnb
= x
n
mb
+ v
m
; x
mnc
= x
n
mc
+ v
m
; x
mnd
= x
n
md
+ v
m
;
x
mra
= x
r
ma
+ a
m
· x
n
ma
+ c
m
; x
mrb
= x
r
mb
+ a
m
· x
n
mb
+ c
m
;
x
mrc
= x
r
mc
+ a
m
· x
n
mc
+ c
m
; x
mrd
= x
r
md
+ a
m
· x
n
md
+ c
m
;
x
msa
= x
s
ma
+ d
m
· x
r
ma
+ e
m
· x
n
ma
+ f
m
;
x
msb
= x
s
mb
+ d
m
· x
r
mb
+ e
m
· x
n
mb
+ f
m
;
№
Уровни
факторов
х
о
x
mn
x
mr
x
ms
у
1
a
+1
x
mn,1
= x
mnа
x
mr,1
= x
mrа
x
ms,1
= x
msа
y
1
= y
a
2
b
+1
x
mn,2
= x
mnb
x
mr,2
= x
mrb
x
ms,2
= x
msb
y
2
= y
b
3
с
+1
x
mn,3
= x
mnc
x
mr,3
= x
mrc
x
ms,3
= x
msc
y
3
= y
c
4
d
+1
x
mn,4
= x
mnd
x
mr,4
= x
mrd
x
ms,4
= x
msd
y
4
= y
d

93
x
msc
= x
s
mc
+ d
m
· x
r
mc
+ e
m
· x
n
mc
+ f
m
;
x
msd
= x
s
md
+ d
m
· x
r
md
+ e
m
· x
n
md
+ f
m
.
Для сокращения дальнейших записей введены следующие обозначе-
ния средних арифметических величин:
(
)
4/
n
md
n
mc
n
mb
n
ma
n
m
xxxxx +++= ;
(
)
4/
r
md
r
mc
r
mb
r
ma
r
m
xxxxx +++= ;
(
)
4/
sn
md
s
mc
s
mb
s
ma
s
m
xxxxx +++= ;
(
)
4/
22222 n
md
n
mc
n
mb
n
ma
n
m
xxxxx +++= ;
(
)
4/
22222 r
md
r
mc
r
mb
r
ma
r
m
xxxxx +++= ;
(
)
4/
22222 s
md
s
mc
s
mb
s
ma
s
m
xxxxx +++= ;
(
)
4/
rn
md
rn
mc
rn
mb
rn
ma
rn
m
xxxxx
+++++
+++= ;
(
)
4/
sn
md
sn
mc
sn
mb
sn
ma
sn
m
xxxxx
+++++
+++= ;
(
)
4/
sr
md
sr
mc
sr
mb
sr
ma
sr
m
xxxxx
+++++
+++= ;
(
)
4/
mdmcmbmam
xxxxx +++= .
Ортогональность матрицы планирования (см. табл.28) обеспечивает-
ся в том случае, если
0
=
+
+
+
mndmncmnbmna
xxxx ,
0
=
+
+
+
mrdmrcmrbmra
xxxx ,
0
=
+
+
+
msdmscmsbmsa
xxxx ,
0
=
⋅
+
⋅
+
⋅
+⋅
mrdmndmrсmnсmrbmnbmramna
xxxxxxxx ,
0
=
⋅
+
⋅
+
⋅
+⋅
msdmndmsсmnсmsbmnbmsamna
xxxxxxxx ,
0
=
⋅
+
⋅
+
⋅
+⋅
msdmrdmsсmrсmsbmrbmsamra
xxxxxxxx .
После подстановки в эти уравнения значений слагаемых, замены по-
лучаемых сумм средними арифметическими величинами и сокращения
одинаковых величин получится система из шести уравнений, по которой
определяются шесть коэффициентов ортогонализации.
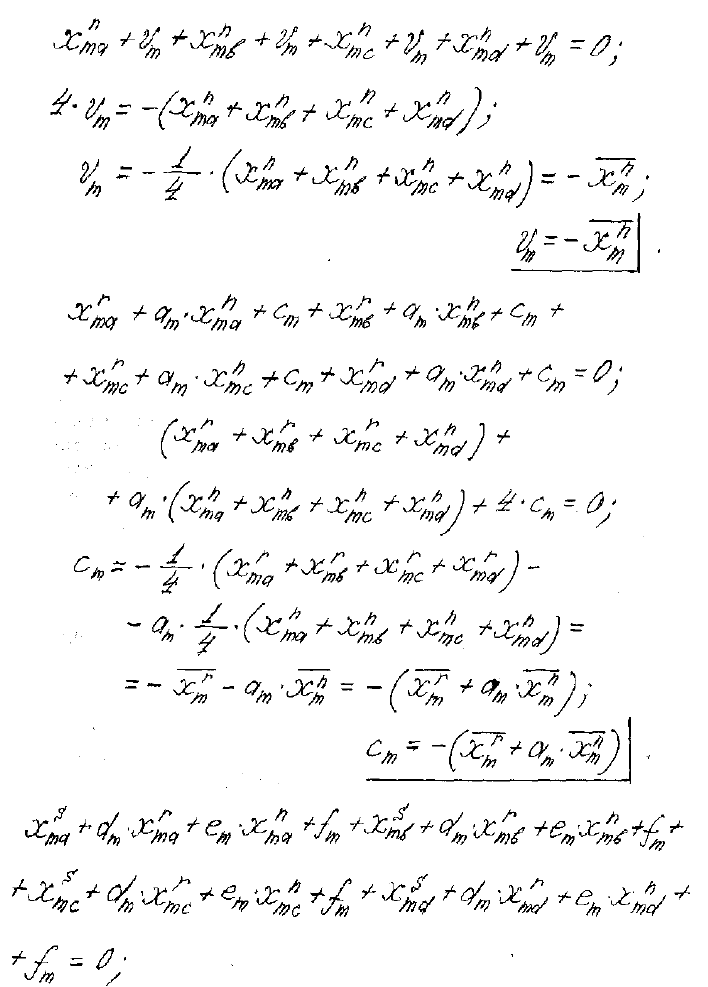
94
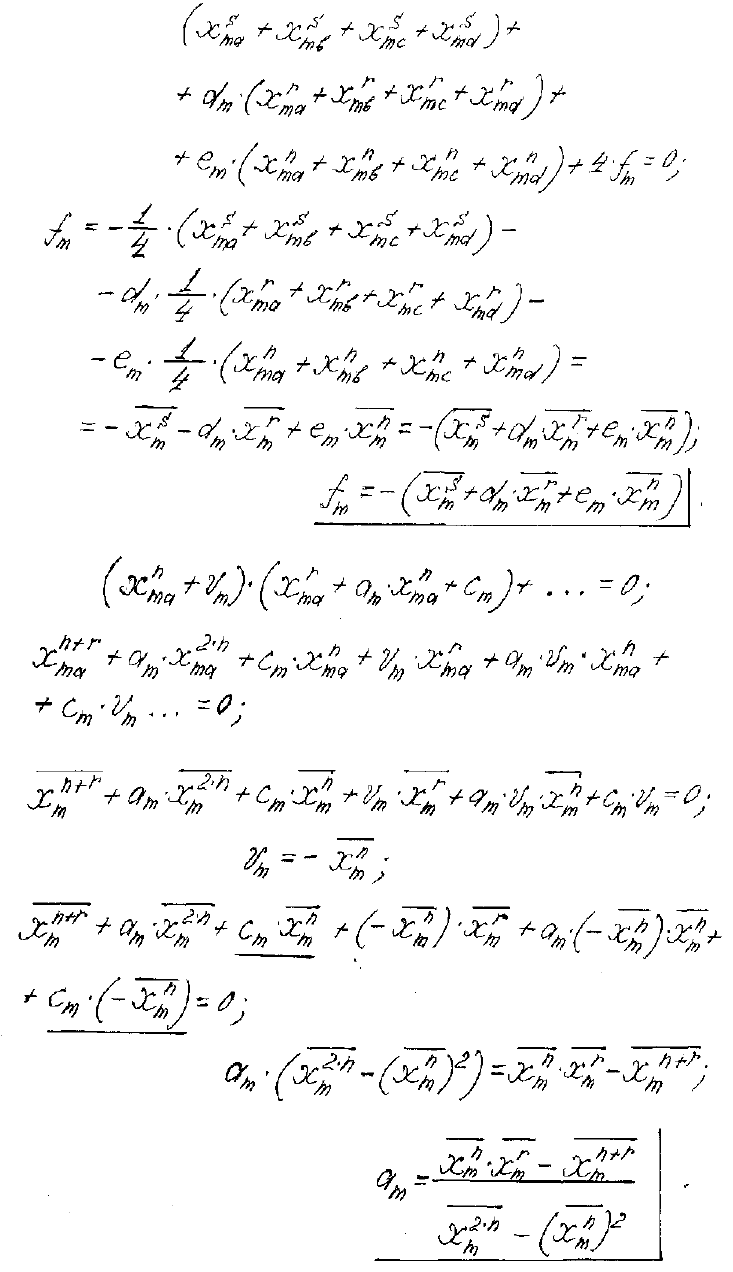
95
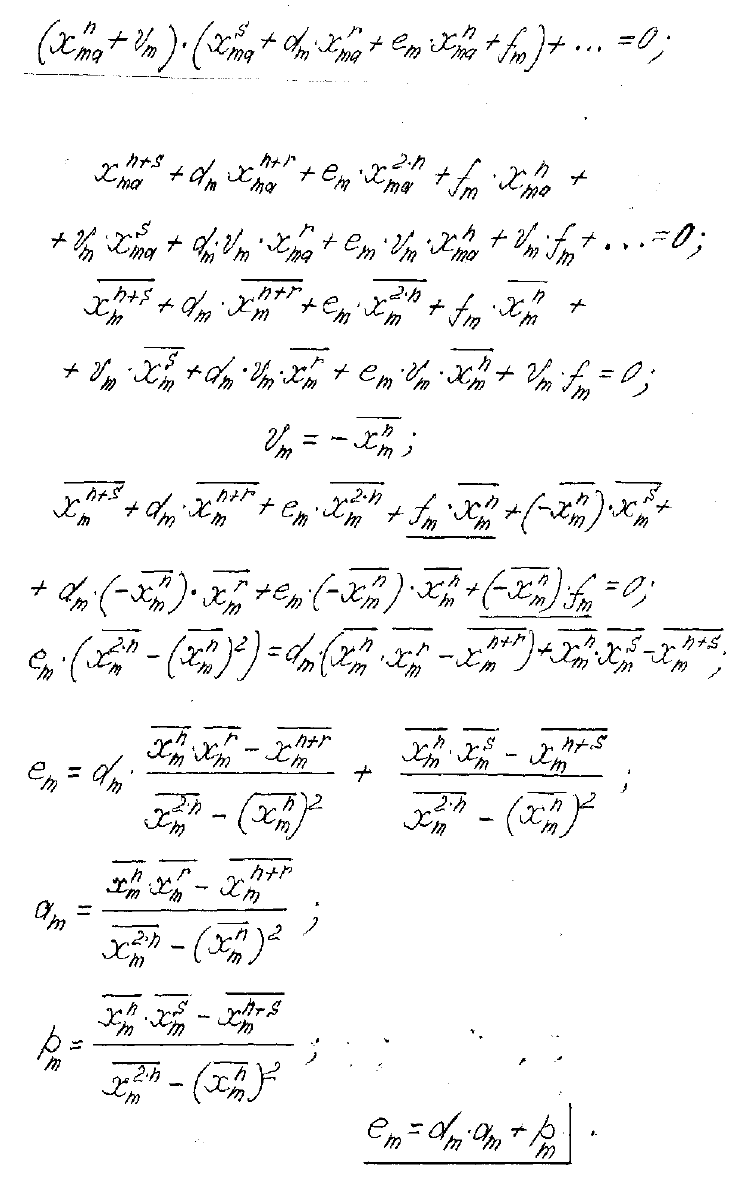
96
97
98
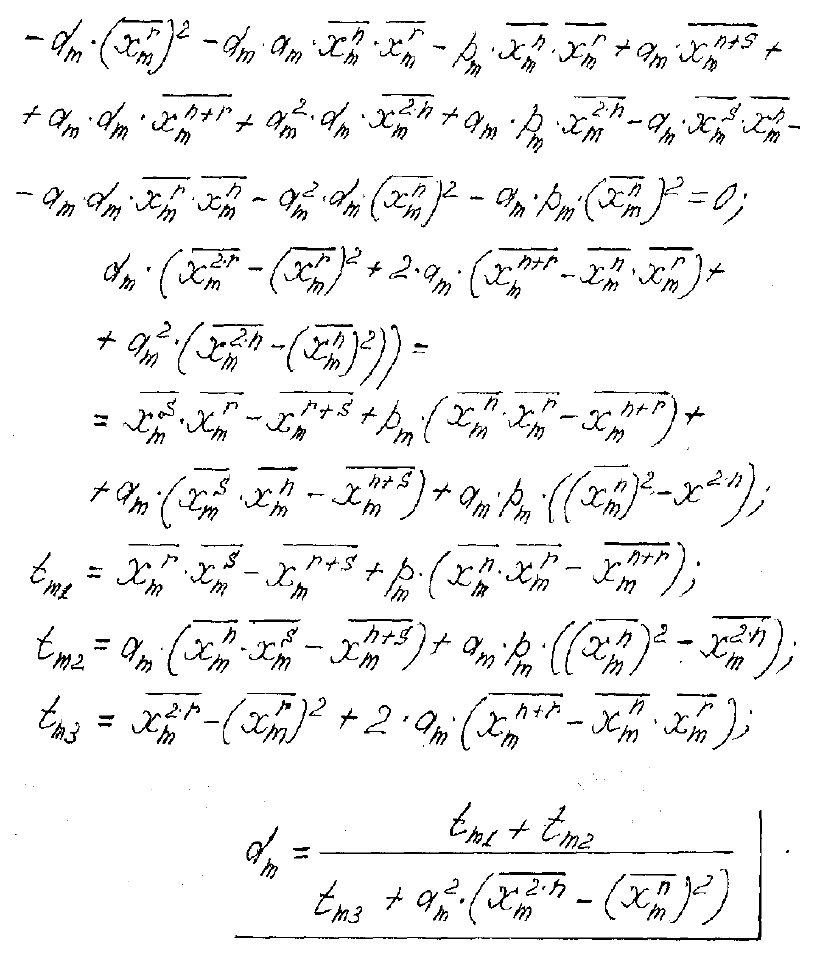
99

100
n
mm
хv −= ; (31)
()
2
2 n
m
n
m
rn
m
r
m
n
m
m
xx
xxx
a
−
−⋅
=
+
; (32)
(
)
n
mm
r
mm
xaxc ⋅+−= ; (33)
()
2
2 n
m
n
m
sn
m
s
m
n
m
m
xx
xxx
P
−
−⋅
=
+
;
(
)
rn
m
r
m
n
mm
sr
m
s
m
r
mm
xxxPxxxt
++
−⋅⋅+−⋅=
1
;
])[()(
22
2
n
m
n
mmm
sn
m
s
m
n
mmm
xхPaxxxat −⋅⋅+−⋅⋅=
+
;
)(2)(
22
3
r
m
n
m
rn
mm
r
m
r
mm
xxxaxxt ⋅−⋅+−=
+
;
])([
222
3
21
n
m
n
mmm
mm
m
xxat
tt
d
−⋅+
+
= ; (34)
mmmm
Pade
+
⋅
=
; (35)
)(
n
mm
r
mm
s
mm
xexdxf ⋅+⋅+−= . (36)
Полученные выше зависимости предназначены для приближенных
вычислений на ЭВМ.
Подстановка в уравнение (30) и в матрицу планирования (см.
табл.28) рассчитанных по формулам (31) – (36) величин коэффициента ор-
тогонализации обеспечивает ортогональность планирования эксперимен-
тов на четырех уровнях факторов.
В связи с ортогональным планированием коэффициенты регрессии
уравнения (30) и дисперсии в определении коэффициентов регрессии рас-
считываются независимо
друг от друга по формулам:
()
dсba
u
u
u
uo
u
uuo
o
уyyyy
x
yx
b +++⋅=⋅=
⋅
=
∑
∑
∑
=
=
=
4
1
4
1
4
1
4
1
2
,
4
1
,
'
; (37)
()
22224
1
2
,
4
1
,
mndmncmnbmna
dmndcmncbmnbamna
u
umn
u
uumn
mn
xxxx
yxyxyxyx
x
yx
b
+++
⋅+⋅+⋅+⋅
=
⋅
=
∑
∑
=
=
; (38)
