Чернов В.П. Математические модели и методы в экономике и менеджменте
Подождите немного. Документ загружается.


91
Пример транспортной задачи
Имеется два пункта производства продукции: «Северный» и «Юж-
ный». Эти пункты способны производить ежемесячно 1,5 тыс. тонн и 2
тыс. тонн продукции, соответственно.
Имеется три пункта потребления этой продукции: «Горный»,
«Озерный» и «Лесной». Ежемесячные потребности этих пунктов в про-
дукции составляют соответственно 0,8 тыс. тонн, 1,6 тыс. тонн и 1 тыс.
тонн. Стоимость транспортирования 1 тонны груза от пункта произ-
водства к пункту потребления представлена в таблице 1.12.
Требуется построить математическую модель для определения та-
кого плана перевозки грузов, с которым были бы связаны наименьшие
затраты на перевозку.
Для удобства записи обозначим пункты производства числами 1 и
2 и пункты потребления числами 1, 2 и 3. Построение модели начнем
с введения переменных. Обозначим посредством хij объем перевозки
(в тоннах) от i-го пункта производства к j-му пункту потребления.
Индекс i принимает одно из двух значений 1 или 2, а индекс j –
одно из трех значений 1, 2 или 3. Таким образом, мы ввели 6 перемен-
ных. Из них, например, переменная х
11
соответствует объему перевозок
от 1-го пункта производства («Северный») к 1-му пункту потребления
(«Горный»), а переменная х
23
– объему перевозок от 2-го пункта произ-
водства («Южный») к 3-му пункту потребления («Лесной»).
Таблица 1.12
Затраты на транспортировку 1 т груза
Пункт
назначения
Пункт
отправления
1. «Горный»
2. «Озерный»
3. «Лесной»
1. Северный 90 80 50
2. Южный 100 120 110
Набор значений переменных х
ij
– это и есть план перевозок. По-
скольку переменные имеют по два индекса, то план удобнее записы-
вать не в виде вектора, а в виде матрицы:
232221
131211
xxx
xxx
X .
92
Математическая модель задачи записывается в следующем виде.
11 12 13 21 22 23
11 12 13
21 22 23
11 21
12 22
13 23
11 12 13
21 22 23
min(90x 80x 50x 100x 120x 110x )
x x x 1500
x x x 2000
x x 800
x x 1600
x x 1000
x 0, x 0, x 0
x 0, x 0, x 0
Целевая функция задачи представляет собой сумму произведений
стоимостей перевозки 1 т груза на объем перевозки для каждой пары
поставщика-потребителя, то есть общую суммарную стоимость всех
перевозок, соответствующих плану Х. Эту суммарную стоимость сле-
дует минимизировать при условии, что будут выполнены все ограниче-
ния.
Ограничения на перевозки можно разбить на три группы. Первая
группа – это верхние два неравенства. В каждое из них входят пере-
менные с одним и тем же первым индексом, но различными вторыми
индексами, то есть переменные, соответствующие одному и тому же
пункту производства, но различным пунктам потребления. Каждое из
этих неравенств говорит о том, что суммарный объем всех грузов, вы-
возимых из одного и того же пункта производства в разные пункты по-
требления, не превосходит того количества продукции, которое может
быть произведено в данном пункте производства.
Вторая группа – это следующие три неравенства. В каждое из них
входят переменные с одним и тем же вторым индексом, но разными
первыми индексами. Эти переменные соответствуют одному пункту
потребления, но разным пунктам производства. Такое неравенство ут-
верждает, что объем всего груза, который свозится из разных пунктов
производства в один и тот же пункт потребления, должен быть не
меньше, чем объем потребности в данном пункте потребления.
Наконец, третья группа ограничений утверждает, что все объемы
перевозок неотрицательны.
.
93
В данной задаче сумма грузов, имеющихся во всех пунктах произ-
водства (3500 т) больше, чем сумма потребностей в грузах, имеющихся
во всех пунктах потребления (3400 т). Такая транспортная задача имеет
оптимальный план перевозок. Как найти такой оптимальный план –
этим вопросом мы займемся позже, но такой план существует. А вот
если бы оказалось наоборот, если бы суммарный груз в пунктах произ-
водства оказался меньше суммарной потребности в пунктах потребле-
ния, то задача оказалась бы неразрешимой. Она не имела бы даже до-
пустимых планов, и тем более не имела бы оптимального.
Если же суммарный груз в пунктах производства в точности равен
суммарной потребности в пунктах потребления, то задача имеет реше-
ние, и ее математическая модель в этом случае может быть приведена к
более удобной форме.
В этом случае из пунктов производства должно быть вывезено все.
Это значит, что ограничения первой группы, связанные с пунктами
производства, должны выполняться в форме равенства. Точно так же и
пункты потребления не могут быть в этом случае удовлетворены с из-
бытком. Следовательно, и ограничения второй группы должны выпол-
нятся в форме равенства.
Таким образом, если, например, потребность третьего пункта по-
требления равна не 1000 т, а 1100 т, так что суммарный груз в пунктах
производства (3500 т) равен суммарной потребности в пунктах потреб-
ления (тоже 3500 т), то в математической модели неравенства первых
двух групп ограничений могут быть заменены равенствами. Модель в
этом случае будет иметь следующий вид:
11 12 13 21 22 23
11 12 13
21 22 23
11 21
12 22
13 23
11 12 13
21 22 23
min(90x 80x 50x 100x 120x 110x )
x x x 1500
x x x 2000
x x 800
x x 1600
x x 1100
x 0, x 0, x 0
x 0, x 0, x 0
Неравенства, связанные с пунктами производства и потребления,
заменены здесь равенствами. Модель транспортной задачи с ограниче-
.

94
ниями-неравенствами называется открытой моделью. Модель с огра-
ничениями-равенствами носит название закрытой модели.
Общий вид транспортной задачи
В общем случае имеется m пунктов производства и n пунктов
потребления. Пункты производства пронумеруем числами от 1 до m.
Номер пункта производства будем обозначать буквой i (таким образом,
1 i m). Пункты потребления пронумеруем числами от 1 до n. Номер
пункта потребления будем обозначать буквой j (таким образом, 1 j n).
Рассмотрим некоторый период времени (например, месяц). Пусть a
i
–
объем производства за период времени в i-м пункте производства, b
i
–
количество продукции, требуемое за период времени в j-м пункте по-
требления. Пусть c
ij
– стоимость перевозки единицы груза из i-го пунк-
та производства в j-й пункт потребления.
Требуется определить план перевозок, удовлетворяющий условиям
по пунктам производства и потребления и соответствующий наимень-
шим затратам на перевозки.
Для построения математической модели следует ввести перемен-
ные. Для каждой пары поставщик-потребитель, то есть для каждой па-
ры (i, j), введем переменную х
ij
– объем перевозки от пункта производ-
ства i к пункту потребления j.
Математическая модель транспортной задачи записывается
следующим образом:
n m
ij ij
j 1 i 1
n
ij i
j 1
m
ij j
i 1
ij
min c x
x a (i 1,m)
x b ( j 1,n)
x 0 (i 1,m; j 1,n)
Целевая функция модели представляет собой общую стоимость
всех перевозок. Она записана в виде двойной суммы. Внутренняя сум-
.
95
ма соответствует пунктам производства, внешняя – пунктам потребле-
ния. Разумеется, эти знаки суммирования в целевой функции можно
поменять местами. От перегруппировки слагаемых сумма не изменяет-
ся.
В модели указано, что целевую функцию следует минимизировать.
Таким образом, модель предписывает искать план перевозок наимень-
шей общей стоимости.
В системе ограничений представлены три группы неравенств. В
первой группе m неравенств, соответствующих пунктам производства.
Каждое неравенство утверждает, что из соответствующего пункта не
может быть вывезено больше, чем в нем имеется. Во второй группе n
неравенств, соответствующих пунктам потребления. Каждое из них
требует, чтобы в соответствующий пункт было привезено не меньше,
чем требуется. В третьей группе m n неравенств, обеспечивающих
неотрицательность объема перевозок.
Представленная модель транспортной задачи с ограничениями-
неравенствами называется открытой моделью. Задача разрешима в
том и только в том случае, когда общий объем груза у поставщиков не
меньше суммарной потребности потребителей, то есть когда выполне-
но неравенство:
m n
i j
i 1 j 1
a b
.
Если выполнено обратное неравенство, то есть если
m n
i j
i 1 j 1
a b
,
то задача неразрешима, для нее не существует не только оптимального,
но даже и допустимого плана.
Если общий объем груза у поставщиков в точности равен общей
потребности потребителей, то есть если имеет место равенство
m n
i j
i 1 j 1
a b
,
то указанная выше открытая модель эквивалентна более простой за-
крытой модели, в которой основные неравенства заменены равенст-
вами. Закрытая модель имеет следующий вид:

96
n m
ij ij
j 1 i 1
n
ij i
j 1
m
ij j
j 1
ij
min c x .
x a (i 1,m),
x b (j 1,n),
x 0 (i 1,m; j 1,n).
Моделирование транспортной задачи средствами Excel
Задание 1.8
Ниже приведены образцы решения транспортной задачи средства-
ми процедуры Поиск решения в Excel.
Постройте в Excel аналогичную таблицу и проведите расчеты.
Задание 2.9
Теневая цена четвертого пункта отправления равна 2, допустимое
увеличение 620, допустимое уменьшение 300. Теневая цена последнего
пункта назначения равна 23, допустимое увеличение 600, допустимое
уменьшение 1310.
Каков смысл величин теневой цены в данной задаче? Как можно
использовать эту информацию при принятии решений?
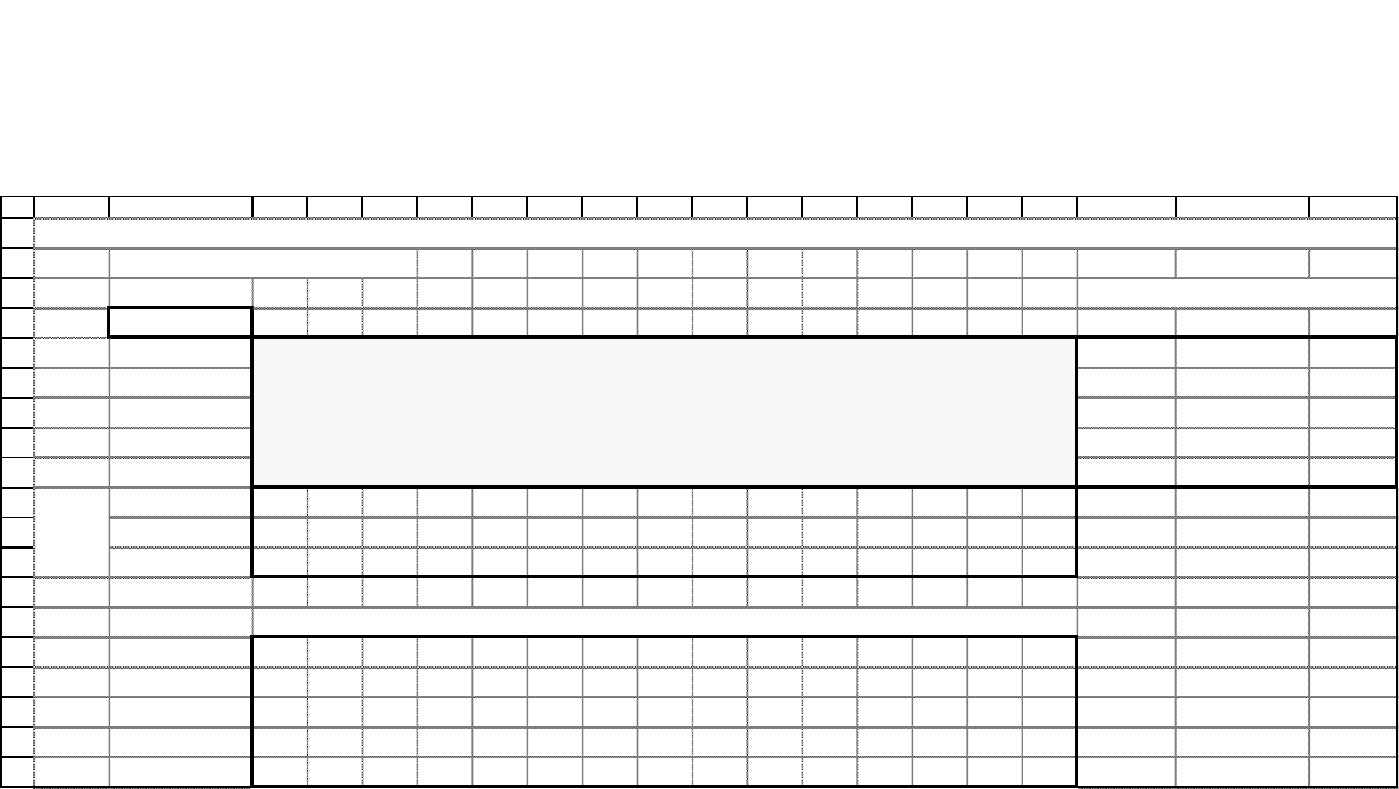
97
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
A B C D E F G H I J K L M N O P Q R S T
Минимальные с уммарные затраты
0
План {x
ij
}
Отправка
Возможности
Остатки
0 1800 1800
0 1200 1200
0 4000 4000
0 300 300
0 4500 4500
Доставка
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Потребности
720 850 1150 230 530 410 480 590 1230 960 880 550 710 400 1310
Остатки
720 850 1150 230 530 410 480 590 1230 960 880 550 710 400 1310
16 16 17 18 18 20 21 19 20 19 18 20 16 18 18
22 26 25 24 26 21 23 27 23 28 23 24 28 23 25
25 26 23 22 26 23 28 25 25 25 22 23 24 22 25
30 28 26 28 26 27 24 26 22 27 21 26 27 31 29
22 21 23 24 24 26 25 27 24 24 26 25 26 24 23
Модель транспортной задачи до решения
Затраты на перевозку единицы груза {c
ij
}
Пункты
назнач.
Пункты отправления
Рис. 1.28. Модель транспортной задачи, подготовленная к решению
91
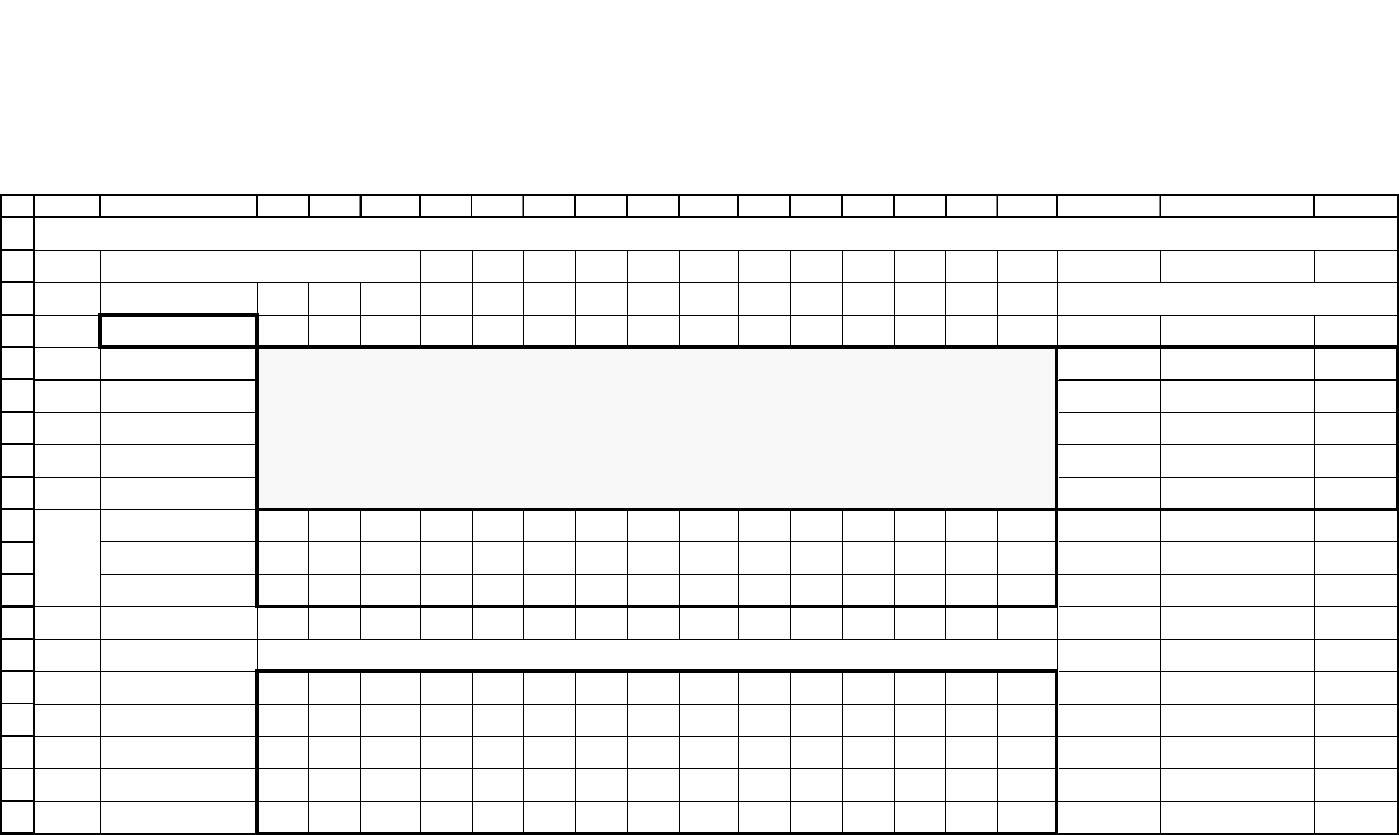
98
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
A B C D E F G H I J K L M N O P Q R S T
Минимальные суммарные затраты
239730
План {x
ij
}
Отправка
Возможности
Остатки
560 0 0 0 530 0 0 0 0 0 0 0 710 0 0
1800
1800
0
0 0 0 0 0 410 480 0 310 0 0 0 0 0 0
1200 1200 0
0 0 1150 230 0 0 0 590 0 0 880 550 0 400 0
3800
4000
200
0 0 0 0 0 0 0 0 300 0 0 0 0 0 0
300 300 0
160 850 0 0 0 0 0 0 620 960 0 0 0 0 1310
3900
4500
600
Доставка
720 850 1150 230 530 410 480 590 1230 960 880 550 710 400 1310
Потребности
720 850 1150 230 530 410 480 590 1230 960 880 550 710 400 1310
Остатки
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
16 16 17 18 18 20 21 19 20 19 18 20 16 18 18
22 26 25 24 26 21 23 27 23 28 23 24 28 23 25
25 26 23 22 26 23 28 25 25 25 22 23 24 22 25
30 28 26 28 26 27 24 26 22 27 21 26 27 31 29
22 21 23 24 24 26 25 27 24 24 26 25 26 24 23
Модель транспортной задачи после решения
Затраты на перевозку единицы груза {c
ij
}
Пункты
назнач.
Пункты отправления
Рис. 1.29. Модель транспортной задачи с результатами решения
92
99
Раздел 2. НЕЛИНЕЙНЫЕ МОДЕЛИ ПЛАНИРОВАНИЯ
Задача максимизации прибыли
Рассмотрим предприятие, которое производит (или покупает) и
продает n видов продукции. Занумеруем все виды продукции числами
от 1 до n. Объем продаж продукции номер j обозначим посредством Q
j
.
Он зависит от цены на эту продукцию и, вообще говоря, от цен на про-
дукцию других видов. Влиянием прочих факторов на объем продаж
пока пренебрежем. Таким образом,
Q
j
= Q
j
(p
1
,…p
j
, p
n
), (1 ≤ j ≤ n)
где p
1
,…p
j
, p
n
– отпускные цены продукции соответствующих видов.
Обозначим вектор цен посредством P, так что P = (p
1
,…p
j
, p
n
). То-
гда предыдущее равенство примет вид:
Q
j
= Q
j
(P). (1 ≤ j ≤ n)
Объем продаж Q
j
не может быть отрицательной величиной, Q
j
≥ 0.
Сами цены тоже не могут быть отрицательными, p
j
≥ 0.
Общие затраты С, связанные с производством (или закупками) и
продажей всех видов продукции, подразделяются на переменную со-
ставляющую V и постоянную составляющую F:
C = V + F,
причем
V(P) =
n
j j
j 1
v Q (P)
.
Выручка от продаж R определяется формулой
R(P) =
n
j j
j 1
p Q (P)
.
Прибыль π есть разность между выручкой и общими затратами
π(P) = R(P) – C(P) =
n
j j
j 1
p Q (P)
–
n
j j
j 1
v Q (P)
– F.
Фирма может устанавливать свои отпускные цены на каждый вид
продукции. Задача состоит в том, чтобы определить такие цены, при
которых общая прибыль фирмы была бы максимальной.
При таких оптимальных ценах затраты фирмы могут выйти за до-
пустимые границы. Обозначим максимальную допустимую величину
затрат посредством S.
Для решения задачи рассмотрим следующую математическую
модель:
100
n
j j
j 1
p Q (P)
–
n
j j
j 1
v Q (P)
– F → max
n
j j
j 1
v Q (P)
+ F ≤ S,
Q
j
(P) 0,
P 0.
Модель предполагает максимизацию прибыли при условии, что
объемы продукции и цены неотрицательны и общие затраты не выхо-
дят за заданные границы.
Отметим, что зависимость Q
j
(P) продаж от цен в общем случае не
предполагается линейной, так что построенная модель представляет
задачу нелинейного программирования. Даже для линейной функции
продаж функция выручки является квадратичной, так что перед нами и
в этом случае будет задача квадратичного программирования.
Решение таких задач можно реализовать средствами Excel.
Рассмотрим для примера относительно простую ситуацию, когда
продажи каждого товара зависят от цены только на этот товар, то есть
будем считать, что
Q
j
= Q
j
(p
j
).
В простейшей ситуации такая зависимость имеет линейный вид:
Q
j
= a
j
p
j
+ b
j
.
Здесь a
j
и b
j
– числовые параметры зависимости объема продаж от це-
ны.
В этой ситуации модель примет простой вид:
n
j j j j
j 1
p (a p b )
–
n
j j j j
j 1
v (a p b )
– F → max
n
j j j j
j 1
v (a p b )
+ F ≤ S,
a
j
p
j
+ b
j
0, (1 ≤ j ≤ n)
p
j
0. (1 ≤ j ≤ n)
Целевая функция задачи имеет вторую степень, а все ограничения
линейны. Перед нами задача квадратичного программирования.
Для обычной продукции естественно предположить, что парамет-
ры удовлетворяют следующим условиям: a
j
< 0 (с ростом цены объем
продаж уменьшается), b
j
> 0 (при нулевой цене объем продаж положи-
телен).
Условие неотрицательности объемов продаж означает, что цена
имеет верхнее предельное значение. Таким образом, цена j-й продук-
