Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

670 Гпава 12

т \''5{M)xdl ^ \''5{M)ydl

У_

^—Ая

• Л1 — X __ Ja

-^с

fb •> Ус сЬ ' Г1)

^ \ 5{M)dl ^ \ 5{M)dl ^^

Ja Ja

где т — масса дуги АВ\ т^,

гПу

— статические моменты этой

дуги относительно осей х,;;; 5{М) —линейная плотность рас-

пределения массы в точке М{х, у)\ dl — дифференциал дуги.

Декартовы координаты центра тяжести

дуги

кривой

урав-

нение которой задано в полярной системе координат 5

8((р),

определяются по формулам

х^=--\'pcoscpdL; Jc=vf P^^^^P^L, (2)

где dL

= yJp +

p d(p — дифференциал дуги; L={ dL — дли-

падуги.

Здесь плотность дуги принята равной единице.

2°.

Координаты центра тяжести криволинейной трапеции,

прилежащей к оси Ох, определяются по формулам

jfi \ 8{M)xydx УУ1 I 8{M)y^dx

•^c

(>b ^ Ус f>b ' K^J

^ I S(M)ydx ^ 2f 5{M)ydx

Ja Ja

где m

—

масса плоской фигуры;

m^,

Шу

— статические моменты

этой фигуры относительно осей х,у.

3°.

Если плоская фигура ограничена линиями у^ =/(л:);

Уг

= fi {^\ х

а;

= Ь

(рис.

12.4),

то координаты центра тяже-

сти определяются по формулам

\''SiM)x{Ux)-f,ix))dx

£а .

l''d(M)(f,(x)-f,(x))dx

х„ =-

Ус

\''S(M)(f,\x)-f,\x))dx

f 5(M)(/,(x)-y;(x))^

(4)

ПРИПОЖЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАПА 671

Здесь 5{М) —поверхностная плотность, т. е. масса едини-

цы площади поверхности фигуры.

Если плотность 5{М) постоянна, то в предьщущих форму-

лах 5 может быть вынесена за знак интегралов и на ее величи-

ну можно сократить.

Если однородная материальная линия или фигура имеет ось

симметрии, то центр тяжести лежит на этой оси.

Координаты центра тяжести криволинейного сектора, ог-

раниченного двумя полярными радиусами и кривой р

р((р),

определяются по формулам

''с=-:^\

P^oscpdcp; у,=—\ р'smcpdcp, (5)

где 5 =

— I

' p^d^ — площадь сектора.

4°.

Расстояние х^ центра тяжести тела от данной плоскости

находится по формуле

xS{x)dx

х.=^.

, (6)

S(x)dx

где S(x)dx — объем элементарого слоя тела на расстоянии х от

плоскости; S(x) — площадь сечения тела плоскостью параллель-

ной данной плоскости и отстоящей от нее на расстоянии х.

Для тела, образованного вращением кривой y

f(x)

(a<x<b) вокруг оси х (рис. 12.18), расстояние х^ центра тяже-

сти от плоскости yOz определяется по формуле

гЬ

ху dx

672 Гпава 12

Расстояние х^ центра тяжести поверхности вращения от

плоскости, перпендикулярной оси

jc,

опредляется по формуле

^у^

_ I

Z^^

^с

- "тг ~

/ ,

г,

• (8)

^ I Wi+(/) ^

J а

5^.

Координаты центра тяжести цилиндрической поверхно-

сти,

перпендикулярной плоскости хОу

(рис.

12.29), образующие

которой ограничены кривой z = z{t), определяются формулами

'•=—• ''=—•

'-^т- <''

где S—площадь цилиндрической поверхности;

т^^,

т^^, т^ —

статические моменты (12.6 (7)) относительно координатных

плоскостей.

6°.

Теоремы Гульдина.

Площадь поверхности, полученной вращением дуги плос-

кой кривой вокруг оси, лежащей в ее плоскости, но ее не пересе-

кающей, равна длине этой дуги, умноженной на длину

окружности, описанной

ее

центром тяжести.

2) Объем тела вращения, образованного вращением плос-

кой фигуры вокруг оси, лежащей в плоскости этой фигуры и ее

не пересекающей, равен произведению площади этой фигуры

на длину окружности, описанной центром тяжести площади фи-

гуры.

7.1.

Найти координаты центра тяжести

дуги:

а) цепной ли-

нии y

ac\i— (0<х<а);\б) арки циклоиды x

a{t-smt),

а{\-cos/), если линейная плотность в каждой ее точке про-

порциональна абсциссе точки; в) кардиоиды p = a(l4-cos^)

{0<(р<к).

Решение, а) Воспользуемся формулами (1), полагая, что

плотность равна

единице.

Для этого найдем дифференциал дуги

ПРИПО?КЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАПА 673

^j\^-y^dx

^\л^^h^—dx=c\i'-'dx, Длина дуги равна

\ а а

L^\

dl=\

ch—(ix^flfsh-

Jo /7

Находим статические моменты:

sh 1.

m,, = I xc\i—dx\ m^=a\ ch^—dx,

У Jo a Jo ^

Интегрируя no частям: x

u, ch—dx

dv; dx

du,

ashxa, будем иметь

m =axsh

— a\

sh—dx = {axsh

a^ch—)

/7 •'0 /7 /7 /7

= a'(shl-chl

+ l).

•i:('

=- Г

ch—

\dx-

—

2 Jo

a ] 2

(

a , 2x

дг

+—sh—

^ 1 ^

l+-sh

Таким образом, координаты центра тяжести дуги будут

х=-^ =

(shl-shl + l) = a

" Z, shl

1-th-

б)

Для определения массы дуги арки циклоиды т при задан-

ной

линейной плотности 5(М) = х найдем дифференциал ее дуги

dl = ^Jx^+y^dt

= sja^

cos

+ a^

sin^ tdt = lasin-dt

и вычислим интеграл

'2л-

^ f

2л:

^ /^ р2л- t pin

xdl

= 2a (t-smt)sm~dt = 2a \ tsm-dt-\ smtsmdt

0 Jo ^ "^ 9 Jo 9 Jo

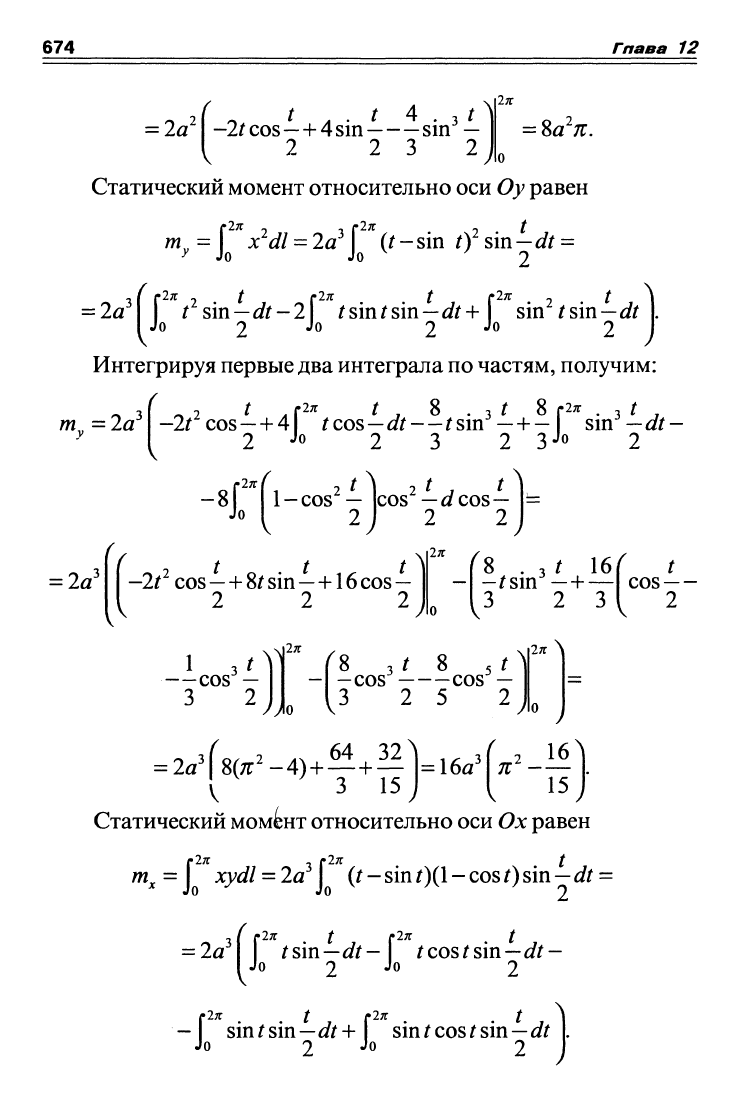
674 Гпава 12

= 2а'

( ^ t л • t 4.3^

—Itcos—l-4sin sin —

(^ 2 2 3 2

1л

= Шп.

Статический момент относительно оси Оу равен

'In , , (1л - t

X dl

2а (t - sin t) sin -dt =

0 Jo ^ ^2

t Sin—a^-2 tsmtsm—dt+l sm

/sin—rf/

Jo 9 Jo 9 Jo 9

= 2a

Интегрируя первые два интеграла по частям, получим:

т„ = 2а

г2ж

-2rcos-

+ 4 tcos-dt—/sin-'-H-

9 Jo '

-€"('-^"^1

if"

sin —dt-

2 З-»» 2

cos^—rfcos—

= 2a'

t t

-2t cos—+8/sin—+ 16cos

8 . 3 / 16

3 2 3

cos

—

Л^

cos —

3 2

2ЛГ

t 8

- -cos COS —

> U 2 5 2,

2я Л

\^ 3 15

= 16a'

К —-

Статический момент относительно оси Ох равен

т^ = xydl

2a J (/-sin/)(l-cos/)sin

—<i/

- ( л2;г / л2;г /

= 2а /sin—Jr- tcostsin—dt-

yjo 2 Jo 2

- [ sin/sin—б//+I sin/cos/sin—J/

Jo 9 Jo

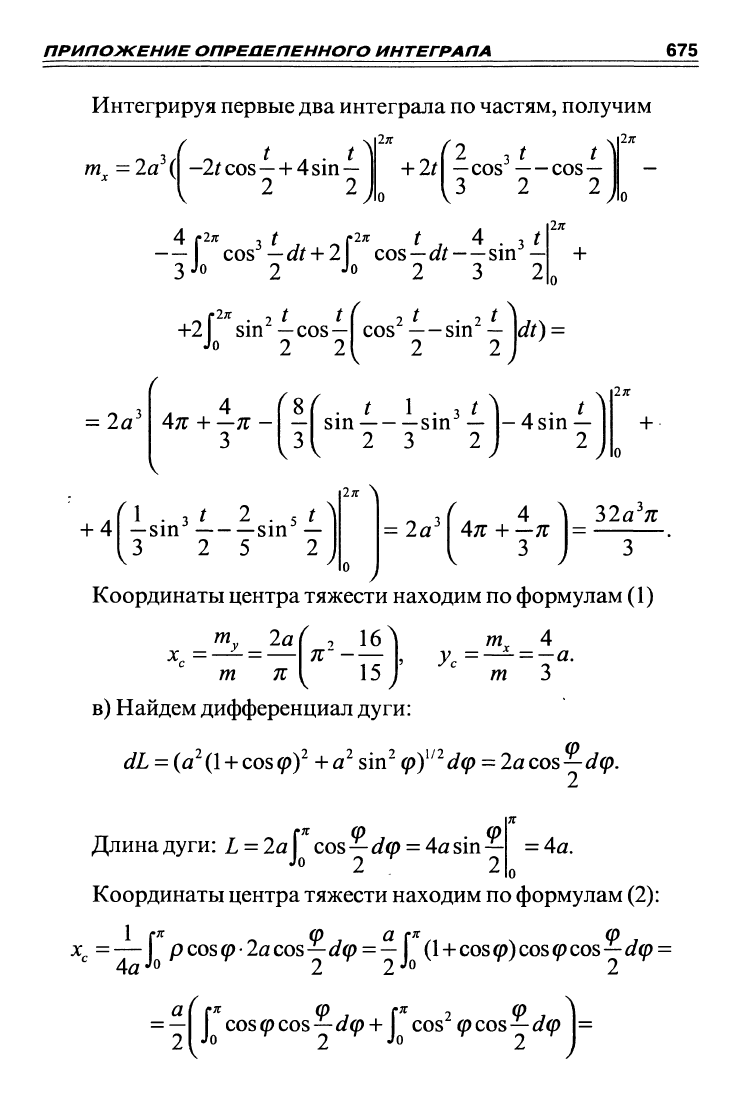
ПРИПОЖЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАПА

675

Интегрируя первые два интеграла по частям, получим

\2к /^ ч|2л:

т^

=2flV ~2^cos

—+

4sin —

2 2

—cos —cos

3 2 2

-1 -

4 f2;r / rlK t , 4.3^

— cos

—a^

cos—at—sin -

3J0 2 Jo 2 3 2

2;r

^ f 2;r ^ ^ t f 2 ^ . 2 О

+2 Sin —COS— cos —sm —

Jo 2 2|^ 2 2)

\dt)

(

= 2a'

л 4 (%^

An +—л: -

. t \ . ъ t

sin sin —

2 3 2

-4sin

—

2;r

+ 4

t 2 .

—sin sin —

,3 2 5 2,

2л:

= 2a'

32a'7i

+—7t

3 3

Координаты центра тяжести находим по формулам (1)

_гп^_2а( . 16^

К"

т к у 15 ^

в) Найдем дифференциал дуги:

т, 4

Л= —= -«•

т 3

.Ф

JZ = {а

-f-

cos (р)

+ а sin (р)

d(p

= 2а

cos—d(p,

Длина

дуги:

Z = 2а J cos—J^ = 4asin^ =4а.

Координаты центра тяжести находим по формулам (2):

jc^

=—J pcos^-2acos—аф =—J (l

cos^)cos^cos—а(р =

—

J cos^cos—<i^ + | cos^^cos—J^ =

676 Гпава 12

^(2rfl-2sin^^Vsin-+2rfl-4sin^^

2-'о(^ 1) 1 ^^\ 2

2<Р

cos —

= а

. (р 2 . ^(р . (р /

sin——sin —+sin—-4

2 3

1.3^ ^ • 59

-sm ——sin —

3 2 5 2

^7 • 9

asm—=

=— psm(p'2acos—a(p =

—

{\ + cos(p)sm(pcos—d(p =

ctf

. (p J f ^ Ф J

—

I sin<pcos—а<рч-1 cos^sinepcos—a(p

^V 2 0 2 ^

-4rcos^^Jcos^-4rf2cos^^-l'|

Jo 2 2 Jol^ 2 J

bos ^Jcos—

= -2a| -cos^^+-cos^ ^ —^

.Ф

cos —

2 3 2

1 ,(p 2

-cos ^

^3 2 5

7.2.

Найти координаты центра тяжести фигуры, ограничен-

= —(2.

ной: а) осью Ох и полуокружностью у = л/а^ - х^; б) осями ко-

ординат и дугой эллипса х = а cos ^ у =

sin

раположеннои в

первом квадран! е, если плотность в каждой ее точке пропорцио-

нальна оси ординат; в)^линиями >^^ = ах и х = а;; г) правой пет-

лей лемнискаты Бернулли р^ -а^ cos

2(j0.

Решение, а) Поскольку полукруг симметричен относитель-

но оси координат, то центр тяжести находится на оси Оу и коор-

дината х^ = О.

Для вычисления координаты у^ воспользуемся формулами

(3).

В знаменателях формул (3) интегралы при 5(М) =

есть не

что

иное,

как площадь фигуры, ограниченной криволинейной тра-

пецией и осью абсцисс. Для полукруга л/а^ - х^

<ix

J—а

ка

ПРИПОЖЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАПА

677

.зЛ

а X —

Л_а_

Таким образом

Ус

=Л-Г /^

Аг {a'-x')dx

= —^

б) Так как плоская фигура прилежит к оси Ох, то восполь-

зуемся формулами (3). Масса плоской фигуры равна w = у dx,

в первом квадранте при возрастании х от

до л величина

убы-

вает от

—

до

О,

поэтому

т = j fe^ sin^ t{ra sin /)t// =

ab^

cos^

t)dt =

'^Л

^/^

^аЪ'

COS/

COS t

V 3 ,

= -a6^

/И,

Найдем статические моменты:

= - f"

y^dx

-\ ,У' sin' t{-a sin

0^?^

= -— f, -

- cos

20^

dt =

l-2cos2/ + -(l + cos40 p =

ab'

?-sin2/ + -

\( 1

f+—sin4/

"/^

= —Ttab ,

Ъ1

'^д;

xy^dx=\ acostb sin

/(-asin/)rf/

= -a 6 I sin /Jsin/ =

= —a о sm /

,0 ^^

"/{ 4

Окончательно получим x^ = —^ =—л, jn = —^ = —^^•

m 8 "" m 64

678

Гпава 12

в) Сделаем чертеж (рис. 12.53). Поскольку парабола сим-

метрична относительно оси х, то

j^^

О .

Уравнения ветвей пара-

болы будут: у = у/ах и у

—sfax . Отсюда по формуле (4) имеем

Рис. 12.53

xyjaxdx 5

_ Jo

\1а.

ах'

^axdx 4 г-

J0 —\/ах

—а.

г) Поскольку правая петля лемнискаты симметрична отно-

сительно оси абсцисс^ то центр тяжести находится на оси Ох и

у^=0.

Для нахождения координаты х^ воспользуемся форму-

лами (5). Площадь петли равна

S = —\\ о d(p = —

XOS 2(pd(p

= —sin

2(р

2^-УА 2 J-^ ^ ^ 4

Таким образом

х^

2 с%

1а СА

mil/ I fi mJl/

р^

COS

(Ddcp

= — y^, (cos

2(fif'^

cos

q>d(p

= ~fj^^(l-2sm'cpf"cos(pd(p.

ПРИПОЖЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАПА

679

Делая замену sin^ =

—prsinf;

cos

(pd(p =

-j=r cos tat при

л:

ЯГ Л'

^ 4 2 ^ 4

t--—, получим

^ VL r-X

^^^4^^^^

V2a r/^fi + 2cos2/ +

-!-(l +

cos4/) V =

J-^ 12

J-^^^l^

2 J

V2a

+ sin It +

Л-—sin4/

Уг

л]2па

7.3.

На каком расстоянии от основания лежит центр тяжес-

ти:

а)

тела,

ограниченного параболоидом вращения

плоскостью,

перпендикулярной его оси, если высота параболоида равна Я;

б) конуса, высота которого равна Я; в) полушара радиуса Ю

Решение, а) Поскольку параболоид образован вращением

кривой

j;^

вокруг оси Ох, то для нахождения центра тяжес-

ти воспользуемся формулой (7)

х„ =

ху dx ^^^ X dx ^2х'

лЯ 2 ^ f^ ~ ^v^

\ У dx I xdx ^-^

Следовательно, от плоскости основания центр тяжести ле-

жит на расстоянии — Я .

б) Для нахождения центра тяжести конуса воспользуемся

результатами задачи 6.7,а

(рис.

12.46).

Так как объем конуса ра-

1 ->

вен V ^—TiRH ,то координата центра тяжести находится по

формуле

х^

=-^- = — = —Я.

' V ПкК'Н 4